Дисперсия и ее свойства.
Среднее квадратическое отклонение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Дисперсия и формула для ее вычисления
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.
На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. M[X-M(X)], для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Так и поступают на деле. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще всего идут по другому пути, то есть вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
Дисперсией называется
математическое ожидание квадрата отклонения случайной величины
от
:
Для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.
Для вычисления дисперсии
на практике удобно пользоваться следующей формулой:
Свойства дисперсии
Свойство 1.
Дисперсия равна разности между
математическим ожиданием квадрата случайной величины
и
квадратом ее математического ожидания.
Свойство 2.
Дисперсия константы
равна нулю:
Свойство 3.
Постоянный множитель
выносится из-под знака дисперсии в квадрате:
Свойство 4.
Дисперсия суммы
случайных величин:
где
–
ковариация случайных величин
и
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Следствия из свойств дисперсии.
В частности, если
и
независимы, то
Прибавление константы
в
случайной величине не меняет ее дисперсии:
Дисперсия разности равна сумме дисперсий:
Среднеквадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Стандартное (среднее
квадратичное) отклонение случайной величины
определяется
как корень из дисперсии и обозначается
Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то ее размерность совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то среднее квадратичное отклонение X будет выражаться также в линейных метрах, a дисперсия X – в квадратных метрах.
Смежные темы решебника:
- Математическое ожидание и его свойства
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
В коробке 20 конфет, из которых 4 с
вареньем. Х – число конфет с вареньем среди двух случайно выбранных. Найти
дисперсию случайной величины Х.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Случайная
величина
– число конфет с вареньем, может принимать
значения 0,1,2
Найдем
соответствующие вероятности:
Проверка:
Получаем
следующий закон распределения СВ
:
Математическое
ожидание:
Дисперсию
можно вычислить по формуле:
Искомая
дисперсия:
Пример 2
Даны
законы распределения независимых случайных величин X и Y:
и
Найти
закон распределения суммы (X+Y). Проверить равенство D(X+Y)=D(X)+D(Y).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Распределение суммы
:
Окончательно получаем:
|
|
2 | 3 | 4 | Итого |
|
|
0.2 | 0.5 | 0.3 | 1 |
Вычислим математические ожидания:
Вычислим
дисперсии:
Проверим
равенство
:
Равенство
выполняется.
Пример 3
Вероятность
изготовления бракованной детали на первом станке составляет 3%, на втором
станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.
Решение
Математическое
ожидание биномиального распределения:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 1-м станке:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 2-м станке:
Дисперсия:
Математическое
ожидание числа бракованных деталей:
Дисперсия
числа бракованных деталей:
Ответ:
;
.
Пример 4
Случайные
величины X,Y распределены по закону
Пуассона. Найдите M{(X+Y)2}, если M(X)=40 и
M(Y)=70, а коэффициент корреляции X и Yравен 0,8.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Поскольку
случайные величины
и
распределены по закону Пуассона и известны их
математические ожидания, соответствующие дисперсии равны:
Пользуясь
свойствами математического ожидания и дисперсии:
Подставляя
числовые значения, получаем:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Независимые случайные величины X и Y
заданы следующими законами:
| x | 2.3 | 2.5 | 2.7 | 2.9 |
| p | 0.4 | 0.3 | 0.2 | 0.1 |
Укажите
законы распределения случайной величины X+Y, X-Y и найдите их
математическое ожидание и дисперсию.
Задача 2
Найти
дисперсию, математическое ожидания, среднекваратическое отклонение ДСВ X,
заданной законом распределения.
| x | -5 | 2 | 3 | 4 |
| p | 0,4 | 0,3 | 0,1 | 0,2 |
Написать F(x) и построить ее график.
Задача 3
Случайная
величина X имеет плотность вероятности
Требуется
найти дисперсию Dx.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Вероятность
того, что прибор исправен, равна 0,8. X – число исправных приборов
из двух выбранных. Найти дисперсию случайной величины X.
Задача 5
Случайные
величины X и Y независимы. Найти
дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.
Задача 6
Найти
дисперсию дискретной случайной величины X – числа отказов элемента
некоторого устройства в десяти независимых опытах, если вероятность отказа
элемента в каждом опыте равна 0,9.
Задача 7
Дискретная
случайная величина X имеет только два возможных значения: x1 и x2, причем x2>x1. Вероятность того, что X
примет значение x1, равна 0,6. Найти закон распределения величины X, если
математическое ожидание и дисперсия известны: M(X)=1,4; D(X)=0,24.
Задача 8
Закон
распределения случайной величины ξ имеет вид:
| ξ | -1 | 2 | 3 | 5 |
| P | 1/4 | 1/2 | 1/8 | 1/8 |
Найти функцию распределения случайной величины ξ,
вычислить ее математическое ожидание, дисперсию и среднее квадратическое
отклонение. Вычислить вероятность P{5⁄2<ξ<5}.
Задача 9
Дискретная
случайная величины X принимает лишь два значения. Большее из значений 3
она принимает с вероятностью 0,4. Кроме того, известна дисперсия случайной
величины D(X)=6. Найти математическое
ожидание случайной величины.
Задача 10
Найти
дисперсию по заданному непрерывному закону распределения случайной величины X,
заданному плотностью вероятности
при
и
в остальных точках.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Для оценки рассеяния
возможных значений случайной величины
вокруг ее среднего значения кроме
дисперсии служат и некоторые другие
характеристики. К их числу относится
среднее квадратическое отклонение.
Средним
квадратическим отклонением случайной
величины X
называют
квадратный корень из дисперсии:
![]()
Легко показать, что дисперсия имеет
размерность, равную квадрату размерности
случайной величины. Так как среднее
квадратическое отклонение равно
квадратному корню из дисперсии, то
размерность
![]()
совпадает
с размерностью X.
Поэтому в
тех случаях, когда желательно, чтобы
оценка рассеяния имела размерность
случайной величины, вычисляют среднее
квадратическое отклонение, а не
дисперсию. Например, если X
выражается
в линейных метрах, то
будет
выражаться также в линейных метрах, a
D
(X)
— в квадратных
метрах. Среднее
квадратическое отклонение суммы
взаимно независимых случайных величин
Пусть известны средние квадратические
отклонения нескольких взаимно
независимых случайных величин. Как
найти среднее квадратическое отклонение
суммы этих величин? Ответ на этот вопрос
дает следующая Теорема.
Теорема.
Среднее
квадратическое отклонение суммы
конечного числа взаимно независимых
случайных величин равно квадратному
корню из суммы квадратов средних
квадратических отклонений этих величин:
![]()
![]()
Доказательство.
Обозначим через X
сумму
рассматриваемых взаимно независимых
величин:
![]()
Дисперсия суммы
нескольких взаимно независимых случайных
величин равна сумме дисперсий слагаемых,
поэтому
![]()
Отсюда
![]()
,
или окончательно
![]()
20.Числовые характеристики(мо, дсв,ско) взаимно независимых св. Начальные и центральные моменты. Мо.
Математическое
ожидание дискретной величины- это сумма
произведении возможных величин на их
вероятности, т.е. М(Х)=∑(I
от 1 до n)xipi
М(Х)= ∑ (I
от 1 до ∞)xipi–
при сходимости правой части. Пр-р:Найти
МО числа появления события А в одном
испытании, если вер-сть появления соб-я
А равно р. Решение:X:
x1=1
x2=0;
P:
p
1-p
M(X)=x1*p+x2*(1-p)=1*p+0*(1-p)=p+0=p
Замечание:МО
числа появления события в данном
испытании равна вероятности этого
события. Св-ва:1°.
М(С)=С, где С-const.2°. М(СХ)=СМ(Х), 3°. X,Y-независ
СВ, M(XY)=M(X)M(Y)
Док-во:
X:x1,x2,…,xn;
P:p1,p2,…,pn;
Y:y1,y2,…,yn;
Q:q1,q2,…,qn;
XY:x1y1;x1y2;…;
x1yn;…;
xny1,xny2;;xnynP:p1q1;p1q2;…;p1qn;…;pnq1;pnq2;…;pnqn
M(XY)=x1p1∑
(j
от 1 до m)yjqj+…+xnpn∑
(i
от1 до n)yiqi=(∑
(i
от1 до n)xipi)(
∑ (j
от 1 до m)yjqj)=M(X)M(Y)
ч.т.д Сл-е:
Пусть Хi-независимыеСВ,
где i=1,…,n,тогда
M(П
(i
от1 до n
)Xi)=
П(i
от1 до n
)M(Xi)
4°.M(X+Y)=M(X)+M(Y)
Д-во:
M(X+Y)=(x1+y1)p11+(x2+y2)p12+…=
=x1∑
(i
от 1 до n)
p1i+…+
xn∑
(i
от 1 до n)pni+
y1∑
(j
от 1 до m)p1j+…+
yn∑
(j
от 1 до m)pmj=/∑(j
от 1 до m)p1j=p1;…/=
∑ (i
от1 до n)xipi+
∑ (j
от 1 до m)yjqj=M(X)+M(Y)
МО числа появлении события А в независимых
испытаниях = произведению числа испытаний
на вероятность появления события в
каждом испытании M(X)=n*p
Док-во:при
проведении n испытании допустим, что
событии в 1 испытании=x1;
во 2 испытании=x2;…;в
n
испытании=xn,
тогда X=∑
(i
от1 до n)xi
M(X)=M(∑
(i
от1 до n)xi
)= ∑ (i
от1 до n)M(xi),M(xi)=p,M(X)=
∑ (i
от1 до n)p=pn
ч.т.д. ДСВ.
Дисперсия
дискретной СВ- отклонение СВ от ее МО
называется СВ и определяется как Х-М(Х)
X:
x1,x2,
… ,xn
P:
p1,p2,
… ,pn
X-M(X):
x1-M(X);
x2-M(X);…;
xn-M(X);P:p1,p2,
… ,pn
МО от отклонения от СВ и его МО=0,т.е.
M(X-M(X))=M(X)-M(M(X))=M(X)-M(X)=0
![]()
ДСВ, Д(Х)-называют
МО от квадрата отклонения ее МО, т.е.
Д(Х)=М([X-M(X)]2);
[X-M(X)]2
:
[x1-M(X)]2;[x2-M(X)]2;…;[xn-M(X)]2
P:
p1;
p2;…
;pn;Д(Х)=
∑ (i
от1 до n)[xi-M(X)]2pi;
Д(X)=M(X2
2XM(X)+M2(X))=M(X2)-2M(X)M(X)+M(M2(X))=M(X2)-M2(X),
т.е. Д(X)=M(X2)-M2(X)
Св-ва:1°Д(С)=M([C-M(C)]2)=M(0-0)=M(0)=0
2°Д(СX)=M((CX)2)-M2(CX)=M(C2X2)-C2M2(X)=C2M(X2)-C2M2(X)=C2[M(X2)-M2(X)]=C2
Д(X)
3°Д(X+Y)=
Д(X)+
Д(Y)
Док-во:
Д(X+Y)=M((X+Y)2)-M2(X+Y)=
=M(X2+2XY+Y2)-M(X+Y)M(X+Y)=
=M(X2)+2M(X)M(Y)+M(Y2)-[M(X)+M(Y)]2=M(X2)+M(Y2)+2M(XY)-M2(X)-2M(X)M(Y)-M2(Y)=M(X2)-M2(X)+M(Y2)-M2(Y)=
Д(X)+
Д(Y)
4° Д(X–Y)=
Д(X+(-Y))=
Д(X)+
Д((-1)Y)=
Д(X)+
(-1)2Д(Y)=
Д(X)+
Д(Y)
Пусть производится
n независимых испытаний, вероятность
появления события А-const
и равно p.X-число
появлений события А в n испытаниях.
Д(X)-?.xi-«число»
появления события А в i-ом испытании.
X=x1+x2+…+xn=∑
(i
от 1 до n)
xi
Д(X)=
∑ (i
от 1 до n)
Д(xi)
Д(xi)=M(xi2)-M2(xi)
xi:
0;1 p:1-p;p
xi2:
0;1
M(xi2)=0(1-p)+1p=0+p=p
M(xi)=p
Д(X)=p-p2=p(1-p)=pq,где
q=1-p
Д(X)=npq
СКО.
Средним квадратичным отклонением СВ
называется квадратный корень из дисперсии
этой СВ,т.е. σ=√Д(X)
σ(∑ (i
от 1 до n)xi)=√Д(∑
(i
от 1 до n)xi)=√
∑ (i
от 1 до n)
Д(xi)=√
∑ (i
от 1 до n)σ2(xi)Одинаково
распределенные независимые СВ. xi,i=1,…,n
x(с
чертой)=(1/n)
∑ (i
от 1 до n)
xi–
среднее арифметическое xi1.
M(х(с
чертой))=M((1/n)
∑ (i
от 1 до n)
xi)=(1/n)
∑ (i
от 1 до n)
M(xi)=/
M(xi)=m0(с
чертой)/=(1/n)m0(с
чертой)n=
m0(с
чертой) 2.
Д(х(с чертой))=Д((1/n)
∑ (i
от 1 до n)
xi)=(1/n2)Д(∑
(i
от 1 до n)
xi)=(1/n2)
∑ (i
от 1 до n)Д(xi)=/Д(xi)=d0/=(1/n2)d0n=d0/n
3. σ(x(с
чертой))=√Д(x(с
чертой))=√(d0/n)=σ0/√n
, σ0=√
d0
Начальные и
центральные теоретические моменты.
Начальным
моментом к СВ X наз-ют МО Х в к-ой степени,
т.е. νк=М(хк),
частные случаи ν1=М(Х),ν2=М(Х2)
Д(Х)=ν2-ν12
Центральным
моментом к СВ Х называют МО (X-M(X))
в к-ой степени, т.е. μк=M([X-M(X)]k),
частные случаи μ1=M(X-M(X))=0,
μ2=M([X-M(X)]2)=
=Д(Х), μ2=ν2-ν12,μ3=ν3-3ν2ν1+2ν13,μ4=ν4-4ν3ν1+6ν2ν12-3ν14
21.Законы
больших чисел. Неравенство и теорема
Чебышева (Чебышев
Пафнутий Львович (1821 – 1824) – русский
математик.) На практике сложно сказать
какое конкретное значение примет
случайная величина, однако, при воздействии
большого числа различных факторов
поведение большого числа случайных
величин практически утрачивает случайный
характер и становится закономерным. Этот
факт очень важен на практике, т.к.
позволяет предвидеть результат опыта
при воздействии большого числа случайных
факторов. Однако, это возможно только
при выполнении некоторых условий,
которые определяются законом больших
чисел. К законам больших чисел относятся
теоремы Чебышева (наиболее общий случай)
и теорема Бернулли (простейший случай),
которые будут рассмотрены далее.
Рассмотрим дискретную случайную величину
Х (хотя
все сказанное ниже будет справедливо
и для непрерывных случайных величин),
заданную таблицей распределения:
Требуется
определить вероятность того, что
отклонение значения случайной величины
от ее математического ожидания будет
не больше, чем заданное число e.Теорема.
(Неравенство Чебышева) Вероятность
того, что отклонение случайной величины
Х от ее математического ожидания по
абсолютной величине меньше положительного
числа e, не меньше чем
![]()
.
![]()
Теорема Чебышева:
если последовательность попарно
независимых случайных величин
X1,X2…Xn..имеет
конечные математ ожидания и дисперсии
этих величин равномерно ограничены(не
превышают постоянного числа С ) то
среднее ариф случайных величин сходится
по вероятности к среднему ариф их математ
ожиданий, те если
–любое
положительное число то

В частности, сред
ариф послед попарно независим величин,
дисперсии которых равномерно ограничены
и которые имеют одно и то же матем
ожидание а
те если
– любое положительное число
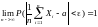
22.Теорема
Бернулли.
Если
в
каждом из n
независимых испытаний .вероятность р
появления события А постоянна
то
как угодно близка к
единице
вероятность того, что-отклонение
относительной
частоты от вероятности р по абсолютной
величине будет сколь
угодно
малым
если ,число
испытаний достаточно велико.
Другими
словами» если
—сколь
угодно
малое положительно число, то при
соблюдении условий теоремы
имеет
место равенство

ЗамечаниеВ
теореме речь идет лишь о вероятности
того, что при достаточно большом числе
испытаний относительная частота будет
как угодно мало отличаться от постоянной
вероятности появления события в каждом
испытании.
Таким
образом, сходимость относительной
частоты т/п
к
вероятности р
отличается
от сходимости в смысле обычного анализа.
Для того чтобы подчеркнуть это различие,
вводят понятие «сходимости по вероятности»
*>. Точнее, различие между указанными
видами сходимости состоит в следующем:
если т/п
стремится
при п—>
к
р как пределу в смысле обычного анализа,
то начиная с некоторого n=
N
для
всех
последующих значений п
неуклонно
выполняется неравенство | т/п—р
<
; если же т/п
стремится
по вероятности к р при
п—>
,
то .для отдельных значений п
неравенство
может не выполняться.
Итак,
теорема Бернулли утверждает, что при
п—>
относительная
частота стремится по вероятноети к р.
Коротко теорему Бернулли записывают
так:
/

Как
видим, теорема Бернулли объясняет,
почему относительная частота при
достаточно большом числе испытаний
обладает свойством устойчивости и
оправдывает статистическое определение
вероятности
Относительной
частотой события наз отношение числа
испытан, в которых событие появилось,
к общему числу фактич произведенных
испытаний.W(A)=m/n
m-число
появ события,n-общее
число испытаний.А различ опытах относ
частоты измен мало, колеблясь около
некоторого постоянного числа.Это постоян
число есть вероятность появлен событ.
*>
Последовательность случайных величин
Xlt
Х2,
..
сходится по вероятности к случайной
величине X,
если
для
любого
> 0 вероятность неравенства Хп
— Х<
при
п—>
стремится
к единице.
23.Функция
распределения вероятностей непрерывной
СВ. Свойства. График функции
распределения.Ф-ией
распред-ия наз-ют ф-ию вида F(x),
определяющую вероятность того, что
случ-ая величина Х в результате испытания
примет значение, меньшее х, т.е. F(x)=P(X<x).
Случ-ую величину наз-ют непрерывной,
если ее ф-ия распределения есть
непрерывная, кусочно-дифференцируемая
ф-ия с непрерывной производной. 1°
Значения ф-ии распределения

[0,1]:
.
Док-во.
Св-во вытекает из определения ф-ии
распределения как вероятности: вероятность
всегда есть неотриц-ое ч-о, не превышающее
1. 2°
F(x)
–неубывающая ф-ия, т.е.

,
если

.
Док-во.
Пусть
.
Событие, состоящее в том, что Х примет
значение,<
,
можно подразделить на =>-ие 2несовместных
события: 1)Х примет значение, <
,
с вероятностью

2)Х примет значение, удовлетворяющее
неравенству

,
с вероятностью

.
По теореме сложения имеем

.
=>
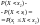
или

.
(*) т.к.
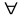
вероятность есть число неотриц-ое, то

,
или
.
=>1.Вероятность
того, что случайная величина примет
значение, заключённое в (a,b),
= приращению ф-ии распределения на этом
интер-ле:
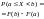
(**).
(это =>-e
вытекает из (*), если
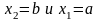
)
=>2.Вероятность
того, что непрерывная случайная величина
Х примет одно определённое значение =
0. 3°.
Если возможные значения случайной
величины

,
то: 1)F(x)=0
при

;
2)F(x)=1
при

.
Док-во.1) Пусть
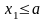
,
тогда событие

невозможно
и, => вероятность = 0. 2)Пусть
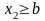
,
тогда событие

достоверно и, => его вероятность = 1. =>.
Если возможные значения непрерывной
случайной величины расположены на всей
оси х, то справедливы =>-ие предельные
соотношения:
;

.
По док-м св-м график расположен в полосе,
огран-ой прямыми у=0 и у=1. При возраст-ии
ч в (a,b),
в к-м заключены все возможные значения
случайной вел-ны, график «подымается
вверх». При

ординаты графика =0; при

— 1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Среднеквадрати́ческое отклонение (среднеквадрати́чное отклонение, стандартное отклонение[1]) — наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания (аналога среднего арифметического с бесконечным числом исходов). Обычно означает квадратный корень из дисперсии случайной величины, но иногда может означать тот или иной вариант оценки этого значения.
В литературе обычно обозначают греческой буквой 


Варианты определения[править | править код]
Обычно определяется как квадратный корень из дисперсии случайной величины: ![{displaystyle sigma ={sqrt {D[X]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c535aeb360aec0139028ee203973550bb364cbb)
На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение, как и математическое ожидание, оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.
В частности, если 



,
то два основных способа оценки стандартного отклонения записываются нижеследующим образом.
Оценка стандартного отклонения на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией[2]):
.
Это в буквальном смысле среднее квадратическое разностей измеренных значений и среднего.
Оценка стандартного отклонения на основании несмещённой оценки дисперсии (подправленной выборочной дисперсии[2], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):
Само по себе, однако, 
Обе оценки являются состоятельными[2].
Кроме того, среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки[3]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии этой оценки.
Среднее значение выборки также является случайной величиной с оценкой среднеквадратичного отклонения[3][]:
Правило трёх сигм[править | править код]

Правило трёх сигм (

.
Практически все значения нормально распределённой случайной величины лежат в интервале 

Интерпретация[править | править код]
Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, для у всех трёх числовых множеств: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8} средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
Практическое применение[править | править код]
На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.
Экономика и финансы[править | править код]
Среднее квадратическое отклонение доходности портфеля ![sigma ={sqrt {D[X]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c535aeb360aec0139028ee203973550bb364cbb)
В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.
Оценка рисков и критика[править | править код]
Среднеквадратическое отклонение широко распространено в финансовой сфере в качестве критерия оценки инвестиционного риска. По мнению американского экономиста Нассима Талеба, этого делать не следует. Так, по теории около двух третей изменений должны укладываться в определённые рамки (среднеквадратические отклонения −1 и +1) и что колебания свыше семи стандартных отклонений практически невозможны. Однако в реальной жизни, по мнению Талеба, всё иначе — скачки отдельных показателей могут превышать 10, 20, а иногда и 30 стандартных отклонений. Талеб считает, что риск-менеджерам следует избегать использования средств и методов, связанных со стандартными отклонениями, таких как регрессионные модели, коэффициент детерминации (R-квадрат) и бета-факторы. Кроме того, по мнению Талеба, среднеквадратическое отклонение — слишком сложный для понимания метод. Он считает, что тот, кто пытается оценить риск с помощью единственного показателя, обречён на неудачу[4].
Климат[править | править код]
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Спорт[править | править код]
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
Пример[править | править код]
Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.
Пусть оценки учеников класса следующие:
.
Тогда средняя оценка равна:
.
Вычислим квадраты отклонений оценок учеников от их средней оценки:
Среднее арифметическое этих значений называется дисперсией:
Стандартное отклонение равно квадратному корню дисперсии:
Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:
и стандартное отклонение равнялось бы:
Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.
Примечания[править | править код]
- ↑ Встречаются также различные синонимы: среднее квадратическое отклонение, стандартный разброс, стандартная неопределённость; термин «среднее квадратическое» означает «среднее степени 2»
- ↑ 1 2 3 Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
- ↑ 1 2 C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — doi:10.1088/1674-1137/40/10/100001.
- ↑ Талеб, Гольдштейн, Шпицнагель, 2022, с. 46.
Литература[править | править код]
- Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов / В. Боровиков. — СПб.: Питер, 2003. — 688 с. — ISBN 5-272-00078-1..
- Нассим Талеб, Дениэл Гольдштейн, Марк Шпицнагель. Шесть ошибок руководителей компаний при управлении рисками // Управление рисками (Серия «Harvard Business Review: 10 лучших статей») = On Managing Risk / Коллектив авторов. — М.: Альпина Паблишер, 2022. — С. 41—50. — 206 с. — ISBN 978-5-9614-8186-0.
Числовые характеристики дискретной случайной величины
В этом разделе:
- Основная информация
- Онлайн калькулятор
- Полезные ссылки
Спасибо за ваши закладки и рекомендации
Основная информация
Числовые характеристики дискретной случайной величины $X$, которые обычно требуется находить в учебных задачах по теории вероятностей, это математическое ожидание $M(X)$, дисперсия $D(X)$ и среднее квадратическое отклонение $sigma(X)$.
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
$$
sigma(X) = sqrt{D(X)}.
$$
Подробные формулы и примеры расчета вы найдете по ссылкам в предыдущем абзаце, в этом же разделе вы сможете автоматически и бесплатно рассчитать эти значения с помощью онлайн-калькулятора, который даст не только ответ, но и продемонстрирует процесс вычисления.
Подробно решим ваши задачи по теории вероятностей
Калькулятор: числовые характеристики случайной величины
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -1.5 или 10.558). Введите нужные значения (убедитесь, что сумма вероятностей равна единице, то есть закон распределения задан верно).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет процесс вычисления математического ожидания $M(X)$, дисперсии $D(X)$ и СКО $sigma(X)$.
- Нужны еще расчеты? Вводите новые числа и нажимайте на кнопку.
Видео. Полезные ссылки
Видеоролики об СКО
На закуску для продвинутых – какие формулы вычисления СКО для выборок бывают и для чего подходят.
Лучшее спасибо – порекомендовать эту страницу
Полезные ссылки
- Калькуляторы по теории вероятнстей
- Онлайн учебник по ТВ
- Примеры решений по теории вероятностей
- Контрольные по теории вероятностей на заказ
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Загрузить PDF
Загрузить PDF
Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.[1]
Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.[2]
Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.
-

1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
-

2
Для вычисления среднего значения понадобятся все числа данного набора данных.[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
-

3
Сложите все числа вашего набора данных.[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
-

4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама
-

1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
-

2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 – 8 = 2; 8 – 8 = 0, 10 – 2 = 8, 8 – 8 = 0, 8 – 8 = 0, и 4 – 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
-

3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
-

4
Сложите квадраты значений, то есть найдите сумму квадратов.[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
-

5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама
-

1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
-

2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
-

3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама
Об этой статье
Эту страницу просматривали 64 743 раза.







