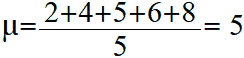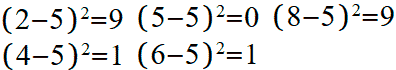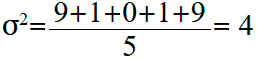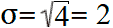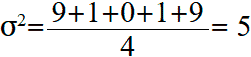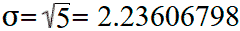Среднее квадратичное отклонение двух, трех, четырех и более чисел. Оно же стандартное отклонение, среднеквадратическое отклонение, среднеквадратичное отклонение, средняя квадратическая, стандартный разброс — показатель рассеивания значений случайной величины относительно её математического ожидания в теории вероятностей и статистике.
Как правило перечисленные термины равны квадратному корню дисперсии.
Пример вычисления стандартного отклонения по следующим формулам:
Вычислим среднюю оценку ученика: 2; 4; 5; 6; 8.
Cредняя оценка будет равна:
Вычисляем квадраты отклонений оценок от их средней оценки:
Вычислим среднее арифметическое (дисперсию) этих значений:
Стандартное отклонение равно квадратному корню дисперсии:
Эта формула справедлива только если эти пять значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки пяти случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 5 нужно было бы поставить n − 1 = 4:
Тогда стандартное отклонение будет равняться:
Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Среднеквадратическое отклонение
begin{align}
& sigma=sqrt{frac{1}{n}sum_{i=1}^N (x_i-bar{x})^2} \
end{align}
Стандартное отклонение
begin{align}
& s=sqrt{frac{n}{n-1}sigma^2}=sqrt{frac{1}{n-1}sum_{i=1}^N (x_i-bar{x})^2} \
end{align}
begin{align}
& где sigma^2-дисперсия; x_i-i-ый элемент выборки; n-объем выборки; bar{x}-среднее арифметическое выборки. \
end{align}
Калькулятор вычислит среднеквадратическое отклонение, а также стандартное отклонение и среднее арифметическое. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.
количество чисел
Среднее квадратичное отклонение
Среднее квадратичное отклонение — это показатель рассеивания значений случайной величины относительно её математического ожидания.
Обозначается символом σ (греческая буква «сигма»).
Среднеквадратичное отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки
среднего арифметического,
при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
Чтобы найти среднеквадратичное отклонение, нужно взять квадратный корень из дисперсии:
Другими словами, среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим.
Данный онлайн калькулятор поможет вычислить среднее квадратичное отклонение ряда значений.
Вводите каждое новое число в отдельную ячейку. Для добавления ячейки нажмите на кнопку со знаком «+».
Поделиться страницей в социальных сетях:
Числовые характеристики дискретной случайной величины
В этом разделе:
- Основная информация
- Онлайн калькулятор
- Полезные ссылки
Понравилось? Добавьте в закладки
Основная информация
Числовые характеристики дискретной случайной величины $X$, которые обычно требуется находить в учебных задачах по теории вероятностей, это математическое ожидание $M(X)$, дисперсия $D(X)$ и среднее квадратическое отклонение $sigma(X)$.
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
$$
sigma(X) = sqrt{D(X)}.
$$
Подробные формулы и примеры расчета вы найдете по ссылкам в предыдущем абзаце, в этом же разделе вы сможете автоматически и бесплатно рассчитать эти значения с помощью онлайн-калькулятора, который даст не только ответ, но и продемонстрирует процесс вычисления.
Подробно решим ваши задачи по теории вероятностей
Калькулятор: числовые характеристики случайной величины
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -1.5 или 10.558). Введите нужные значения (убедитесь, что сумма вероятностей равна единице, то есть закон распределения задан верно).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет процесс вычисления математического ожидания $M(X)$, дисперсии $D(X)$ и СКО $sigma(X)$.
- Нужны еще расчеты? Вводите новые числа и нажимайте на кнопку.
Видео. Полезные ссылки
Видеоролики об СКО
На закуску для продвинутых – какие формулы вычисления СКО для выборок бывают и для чего подходят.
Понравилось? Добавьте в закладки
Полезные ссылки
- Калькуляторы по теории вероятнстей
- Онлайн учебник по ТВ
- Примеры решений по теории вероятностей
- Контрольные по теории вероятностей на заказ
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Среднее квадратичное отклонение измеряет точность подсчетов, выполненных с помощью среднего арифметического. Для нахождения среднего квадратичного отклонения используется сумма разниц каждого отдельного значения от полученного среднего арифметического, возведенных в квадрат, и умноженная на обратное количество значений 1/n, все это помещено под корень второй степени. Таким образом, можно измерить насколько сильно отличается каждый отдельный показатель от среднего значения, и вывести общее отклонение.