Как найти среднее квадратическое отклонение случайной величины

Числовые характеристики дискретной случайной величины

В этом разделе:

Основная информация
Онлайн калькулятор
Полезные ссылки

Полезная страница? Сохрани или расскажи друзьям

Основная информация

Числовые характеристики дискретной случайной величины $X$, которые обычно требуется находить в учебных задачах по теории вероятностей, это математическое ожидание $M(X)$, дисперсия $D(X)$ и среднее квадратическое отклонение $sigma(X)$.

$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
$$
sigma(X) = sqrt{D(X)}.
$$

Подробные формулы и примеры расчета вы найдете по ссылкам в предыдущем абзаце, в этом же разделе вы сможете автоматически и бесплатно рассчитать эти значения с помощью онлайн-калькулятора, который даст не только ответ, но и продемонстрирует процесс вычисления.

Подробно решим ваши задачи по теории вероятностей

Калькулятор: числовые характеристики случайной величины

Введите число значений случайной величины К.
Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -1.5 или 10.558). Введите нужные значения (убедитесь, что сумма вероятностей равна единице, то есть закон распределения задан верно).
Нажмите на кнопку “Вычислить”.
Калькулятор покажет процесс вычисления математического ожидания $M(X)$, дисперсии $D(X)$ и СКО $sigma(X)$.
Нужны еще расчеты? Вводите новые числа и нажимайте на кнопку.

Видео. Полезные ссылки

Видеоролики об СКО

На закуску для продвинутых – какие формулы вычисления СКО для выборок бывают и для чего подходят.

Лучшее спасибо – порекомендовать эту страницу

Полезные ссылки

Калькуляторы по теории вероятнстей
Онлайн учебник по ТВ
Примеры решений по теории вероятностей
Контрольные по теории вероятностей на заказ

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Источник

Среднеквадрати́ческое отклонение (среднеквадрати́чное отклонение, стандартное отклонение^[1]) — наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания (аналога среднего арифметического с бесконечным числом исходов). Обычно означает квадратный корень из дисперсии случайной величины, но иногда может означать тот или иной вариант оценки этого значения.

В литературе обычно обозначают греческой буквой $sigma$ (сигма). В статистике принято два обозначения: $sigma$ — для генеральной совокупности и ${displaystyle sd}$ (с англ. standard deviation — стандартное отклонение) — для выборки.

Варианты определения[править | править код]

Обычно определяется как квадратный корень из дисперсии случайной величины: ${displaystyle sigma ={sqrt {D[X]}}}$ . Измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение, как и математическое ожидание, оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.

В частности, если $x_{i}$ — $i$ -й элемент выборки, $n$ — объём выборки, ${bar {x}}$ — среднее арифметическое выборки (выборочное среднее — оценка математического ожидания величины):

${displaystyle {bar {x}}={frac {1}{n}}sum _{i=1}^{n}x_{i}={frac {1}{n}}(x_{1}+ldots +x_{n})}$ ,

то два основных способа оценки стандартного отклонения записываются нижеследующим образом.

Оценка стандартного отклонения на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией^[2]):

${displaystyle S={sqrt {{frac {1}{n}}sum _{i=1}^{n}left(x_{i}-{bar {x}}right)^{2}}}}$ .

Это в буквальном смысле среднее квадратическое разностей измеренных значений и среднего.

Оценка стандартного отклонения на основании несмещённой оценки дисперсии (подправленной выборочной дисперсии^[2], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):

${displaystyle S_{0}={sqrt {{frac {n}{n-1}}S^{2}}}={sqrt {{frac {1}{n-1}}sum _{i=1}^{n}left(x_{i}-{bar {x}}right)^{2}}}.}$

Само по себе, однако, $S_{0}$ не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.

Обе оценки являются состоятельными^[2].

Кроме того, среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки^[3]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии этой оценки.

Среднее значение выборки также является случайной величиной с оценкой среднеквадратичного отклонения^[3]^[]:

${displaystyle S_{bar {x}}=S_{0}/{sqrt {n}}={sqrt {{frac {1}{n(n-1)}}sum _{i=1}^{n}left(x_{i}-{bar {x}}right)^{2}}}.}$

Правило трёх сигм[править | править код]

Правило трёх сигм ( ${displaystyle 3sigma }$ ) гласит: вероятность того, что любая случайная величина отклонится от своего среднего значения менее чем на ${displaystyle 3sigma }$ :

${displaystyle P(|xi -Exi mid <3sigma )geqslant {frac {8}{9}}}$ .

Практически все значения нормально распределённой случайной величины лежат в интервале ${displaystyle left(mu -3sigma ;mu +3sigma right)}$ , где ${displaystyle mu =Exi }$ — математическое ожидание случайной величины. Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.

Интерпретация[править | править код]

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Например, для у всех трёх числовых множеств: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8} средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.

В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.

Практическое применение[править | править код]

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы[править | править код]

Среднее квадратическое отклонение доходности портфеля $sigma ={sqrt {D[X]}}$ отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Оценка рисков и критика[править | править код]

Среднеквадратическое отклонение широко распространено в финансовой сфере в качестве критерия оценки инвестиционного риска. По мнению американского экономиста Нассима Талеба, этого делать не следует. Так, по теории около двух третей изменений должны укладываться в определённые рамки (среднеквадратические отклонения −1 и +1) и что колебания свыше семи стандартных отклонений практически невозможны. Однако в реальной жизни, по мнению Талеба, всё иначе — скачки отдельных показателей могут превышать 10, 20, а иногда и 30 стандартных отклонений. Талеб считает, что риск-менеджерам следует избегать использования средств и методов, связанных со стандартными отклонениями, таких как регрессионные модели, коэффициент детерминации (R-квадрат) и бета-факторы. Кроме того, по мнению Талеба, среднеквадратическое отклонение — слишком сложный для понимания метод. Он считает, что тот, кто пытается оценить риск с помощью единственного показателя, обречён на неудачу^[4].

Климат[править | править код]

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт[править | править код]

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Пример[править | править код]

Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.

Пусть оценки учеников класса следующие:

${displaystyle 2, 4, 4, 4, 5, 5, 7, 9}$ .

Тогда средняя оценка равна:

${displaystyle mu ={frac {2+4+4+4+5+5+7+9}{8}}=5}$ .

Вычислим квадраты отклонений оценок учеников от их средней оценки:

${displaystyle {begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\end{array}}}$

Среднее арифметическое этих значений называется дисперсией:

${displaystyle sigma ^{2}={frac {9+1+1+1+0+0+4+16}{8}}=4}$

Стандартное отклонение равно квадратному корню дисперсии:

${displaystyle sigma ={sqrt {4}}=2}$

Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:

${displaystyle sigma ^{2}={frac {9+1+1+1+0+0+4+16}{7}}approx 4{,}57}$

и стандартное отклонение равнялось бы:

${displaystyle sigma ={sqrt {4{,}57}}approx 2{,}14}$

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Примечания[править | править код]

↑ Встречаются также различные синонимы: среднее квадратическое отклонение, стандартный разброс, стандартная неопределённость; термин «среднее квадратическое» означает «среднее степени 2»
↑ ¹ ² ³ Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
↑ ¹ ² C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — doi:10.1088/1674-1137/40/10/100001.
↑ Талеб, Гольдштейн, Шпицнагель, 2022, с. 46.

Литература[править | править код]

Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов / В. Боровиков. — СПб.: Питер, 2003. — 688 с. — ISBN 5-272-00078-1..
Нассим Талеб, Дениэл Гольдштейн, Марк Шпицнагель. Шесть ошибок руководителей компаний при управлении рисками // Управление рисками (Серия «Harvard Business Review: 10 лучших статей») = On Managing Risk / Коллектив авторов. — М.: Альпина Паблишер, 2022. — С. 41—50. — 206 с. — ISBN 978-5-9614-8186-0.

Источник

Математическое ожидание, дисперсия, среднее квадратичное отклонение

Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.

Математическое ожидание Mдискретной случайной величины – это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.

Свойства математического ожидания:

Математическое ожидание постоянной
величины равно самой постоянной .
Постоянный множитель можно выносить
за знак математического ожидания .
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий .
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых

Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.

Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.

Принимая во внимание свойства
математического ожидания, легко показать
что

Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.

Свойства дисперсии:

Дисперсия постоянной равна нулю.
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат.
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.

Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное.

Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.

Решение задач:

1)Дана случайная величина Х:

x_i	-3	-2	0	1	2
p_i	0,1	0,2	0,05	0,3	0,35

Найти М(х), D(X).

Решение:

=9=2,31.

2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.

Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.

Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.

Решение:D(Z)=6²D(Х)-2²D(Y)+0=180-8=172.

Тема 7. Непрерывные случайные величины

Задача 14

Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.

Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).

Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.

Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.

Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:

Свойства плотности распределения.

1) Плотность распределения – неотрицательная
функция.

2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.

Решение задач.

1.Случайная величина подчинена
закону распределения с плотностью:

Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до.

Решение:

Для нахождения коэффициента авоспользуемся свойством.

2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).

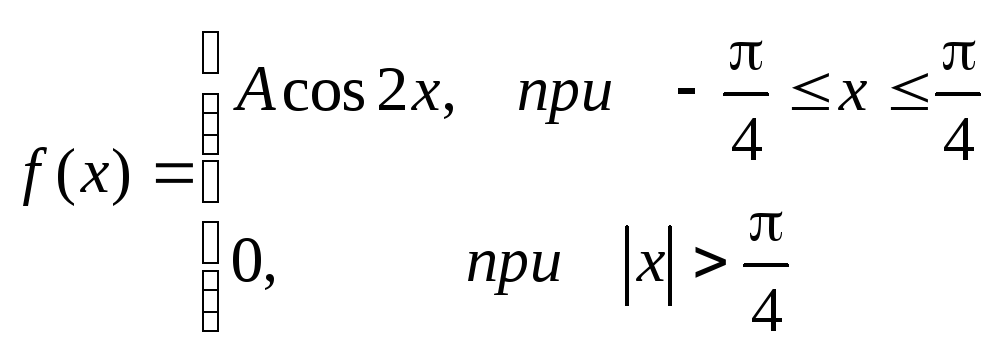
Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал.

Решение:

Найдем коэффициент А.

Найдем функцию распределения:

1) На участке
:

2) На участке

3) На участке

Итого:

Найдем вероятность попадания случайной
величины в интервал
.

Ту же самую вероятность можно искать
и другим способом:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Загрузить PDF

Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.^[1] Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.^[2] Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.

1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.^[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
2
Для вычисления среднего значения понадобятся все числа данного набора данных.^[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
3
Сложите все числа вашего набора данных.^[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.^[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама

1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.^[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.^[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 – 8 = 2; 8 – 8 = 0, 10 – 2 = 8, 8 – 8 = 0, 8 – 8 = 0, и 4 – 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.^[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 2², 0², 2², 0², 0², и (-4)² = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
4
Сложите квадраты значений, то есть найдите сумму квадратов.^[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.^[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама

1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.^[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.^[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.^[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама

Об этой статье

Эту страницу просматривали 64 743 раза.

Была ли эта статья полезной?

Источник

Среднеквадратическое отклонение случайной величины (или СКО случайной величины ) показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения.

Обозначение: σ(X), σ

В регрессионном анализе СКО характеризует достоверность линии тренда для прогнозирования.

Среднеквадратическое отклонение связано с дисперсией случайной величины X и эта связь выражается в виде формулы для определения среднего квадратического отклонения:

Ряд распределения задан в виде таблицы 1

Найти дисперсию и среднее квадратическое отклонение:

Решение

D(X) = M(X²) — M²(X)

Вычисляем математическое ожидание

М(Х)=3·0,2+4·0,5+5·0,3=

=0,6+2,0+1,5=4,1

Представим закон распределения дискретной случайной величины для X²в виде таблицы 2:

Найдем М(Х²) исходя из таблицы 2:

М(Х²)=9·0,2+16·0,5 +25·0,3=

=1,8+8+7,5=17,3

Дисперсия СВ равна:

D(X) = M(X²)-M²(X)=

=17,3-(4,1)² =0,49

Извлекая корень квадратный из дисперсии, найдём среднеквадратическое отклонение случайной величины:

Среднеквадратическое отклонение случайной величины формула пример с решением

17404

Источник

Числовые характеристики дискретной случайной величины

Основная информация

Калькулятор: числовые характеристики случайной величины

Видео. Полезные ссылки

Видеоролики об СКО

Полезные ссылки

Варианты определения[править | править код]

Правило трёх сигм[править | править код]

Интерпретация[править | править код]

Практическое применение[править | править код]

Экономика и финансы[править | править код]

Оценка рисков и критика[править | править код]

Климат[править | править код]

Спорт[править | править код]

Пример[править | править код]

Примечания[править | править код]

Литература[править | править код]

Математическое ожидание, дисперсия, среднее квадратичное отклонение

Тема 7. Непрерывные случайные величины

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Как найти место для укола в ягодицу

Как найти правильный глагол в английском языке

Как найти клона своей страницы вк

Добавить комментарий Отменить ответ