Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.
Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных. Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи — следите за рекламой! Однако сухая теория без инструментов реализации — вещь не сильно полезная. Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.
Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:
— максимальное и минимальное значение
— среднее линейное отклонение
— дисперсия (по генеральной совокупности и по выборке)
— среднее квадратическое отклонение (по генеральной совокупности и по выборке)
— коэффициент вариации
Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.
Максимальное и минимальное значение
Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум — самое большое значение из анализируемого набора данных, минимум — самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам — их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум — весьма информативные показатели. Давайте теперь их рассчитаем в Excel.
Как нетрудно догадаться, делается сие элементарно — как два клика об асфальт. В Мастере функций следует выбрать: МАКС — для расчета максимального значения, МИН — для расчета минимального значения. Для облегчения поиска перечень всех функций можно отфильтровать по категории «Статистические».
Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».
Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение — в разворачивающемся списке.
В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.
Среднее линейное отклонение
Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:
где
a — среднее линейное отклонение,
x — анализируемый показатель, с черточкой сверху — среднее значение показателя,
n — количество значений в анализируемой совокупности данных.
В Excel эта функция называется СРОТКЛ.
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.
Дисперсия
Дисперсия — это средний квадрат отклонений, мера характеризующая разброс данных вокруг среднего значения. Математическая формула дисперсии по генеральной совокупности имеет вид:
где
D — дисперсия,
x — анализируемый показатель, с черточкой сверху — среднее значение показателя,
n — количество значений в анализируемой совокупности данных.
Excel также предлагает готовую функцию для расчета генеральной дисперсии ДИСП.Г.
При анализе выборочных данных, следует использовать выборочную дисперсию, так как генеральная оказывается смещенной в сторону занижения.
Математическая формула выборочной дисперсии имеет вид:
в Excel выборочная дисперсия рассчитывает через функцию ДИСП.В.
Выбираем в Мастере функций нужную дисперсию (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат, поэтому дисперсия сама по себе мало о чем говорит. Ее обычно используют для дальнейших расчетов.
Среднее квадратическое отклонение
Среднеквадратическое отклонение по генеральной совокупности — это корень из генеральной дисперсии.
Выборочное среднеквадратическое отклонение — это корень из выборочной дисперсии.
Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:
— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г
— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.
С названием этого показателя может возникнуть путаница, т.к. часто можно встретить синоним «стандартное отклонение». Пугаться не нужно — смысл тот же.
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднего квадартического отклонения на среднее арифметическое значение. Математическая формула такова:
В Экселе нет готовой функции для расчета коэффициента вариации, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
=СТАНДОТКЛОН.Г(диапазон)/СРЗНАЧ(диапазон)
В скобках должен быть указан диапазон данных. При необходимости используется среднее квадратическое отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на закладке «Главная»:
Изменить формат также можно, выбрав «Формат ячеек» из выпадающего списка после выделения нужной ячейки правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то — неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
В целом, с помощью Excel все, или почти все, статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска в Мастере функций. Ну, и Гугл в помощь.
Легкой работы в Excel и до встречи на блоге statanaliz.info.
Оригинал и другие статьи http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.
Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных. Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи – следите за рекламой! Однако сухая теория без инструментов реализации – вещь не сильно полезная. Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.
Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:
— максимальное и минимальное значение
— среднее линейное отклонение
— дисперсия (по генеральной совокупности и по выборке)
— среднее квадратическое отклонение (по генеральной совокупности и по выборке)
— коэффициент вариации
Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.
Максимальное и минимальное значение
Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.
Как нетрудно догадаться, делается сие элементарно – как два клика об асфальт. В Мастере функций следует выбрать: МАКС – для расчета максимального значения, МИН – для расчета минимального значения. Для облегчения поиска перечень всех функций можно отфильтровать по категории «Статистические».
Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».
Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение – в разворачивающемся списке.
В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.
Среднее линейное отклонение
Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:
где
a – среднее линейное отклонение,
x – анализируемый показатель, с черточкой сверху – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
В Excel эта функция называется СРОТКЛ.
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.
Дисперсия
Дисперсия — это средний квадрат отклонений, мера характеризующая разброс данных вокруг среднего значения. Математическая формула дисперсии по генеральной совокупности имеет вид:
где
D – дисперсия,
x – анализируемый показатель, с черточкой сверху – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Excel также предлагает готовую функцию для расчета генеральной дисперсии ДИСП.Г.
При анализе выборочных данных, следует использовать выборочную дисперсию, так как генеральная оказывается смещенной в сторону занижения.
Математическая формула выборочной дисперсии имеет вид:
в Excel выборочная дисперсия рассчитывает через функцию ДИСП.В.
Выбираем в Мастере функций нужную дисперсию (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат, поэтому дисперсия сама по себе мало о чем говорит. Ее обычно используют для дальнейших расчетов.
Среднее квадратическое отклонение
Среднеквадратическое отклонение по генеральной совокупности – это корень из генеральной дисперсии.
Выборочное среднеквадратическое отклонение – это корень из выборочной дисперсии.
Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:
— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г
— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.
С названием этого показателя может возникнуть путаница, т.к. часто можно встретить синоним «стандартное отклонение». Пугаться не нужно – смысл тот же.
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднего квадартического отклонения на среднее арифметическое значение. Математическая формула такова:
В Экселе нет готовой функции для расчета коэффициента вариации, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
=СТАНДОТКЛОН.Г(диапазон)/СРЗНАЧ(диапазон)
В скобках должен быть указан диапазон данных. При необходимости используется среднее квадратическое отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на закладке «Главная»:
Изменить формат также можно, выбрав «Формат ячеек» из выпадающего списка после выделения нужной ячейки правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
В целом, с помощью Excel все, или почти все, статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска в Мастере функций. Ну, и Гугл в помощь.
Легкой работы в Excel и до встречи на блоге statanaliz.info.
Оригинал и другие статьи http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
В этой статье мы приступим к изучению показателей вариации: размах вариации, межквартильный размах, среднее линейное отклонение.
В математической статистике вариация занимает одно из центральных мест. Что же такое вариация? Это изменчивость. Вариация показателя – изменчивость показателя.
Показатели вариации дают очень важную характеристику процессам и явлениям. Они отражают устойчивость процессов и однородность явлений. Чем меньше показатель вариации, тем более процесс устойчивый, а значит, и более предсказуемый.
Показатели вариации отражают не отдельно взятые значения, а дают характеристику некоторому явлению или процессу в целом. Имея в наличии показатели среднего значения и вариации, можно получить первичное представление о характере данных. Средняя – это обобщающий уровень, а вариация характеризует, насколько среднее значение (или другой показатель) хорошо обобщает значения некоторой совокупности данных. Если показатель вариации незначительный, то значения совокупности находятся близко к среднему, следовательно, среднее значение хорошо обобщает совокупность. Если вариация большая, то среднее значение плохо обобщает данные (значения разбросаны далеко друг от друга), и получается «средняя температура по больнице».
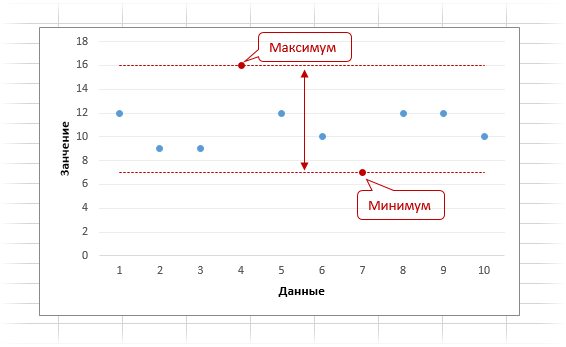
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.
Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Межквартильный размах
В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.
Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».
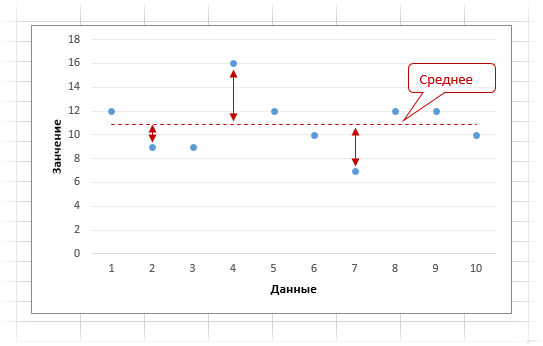
Среднее линейное отклонение
Есть показатели вариации, которые учитывают сразу все значения, а не только отдельные наблюдения (типа максимума или минимума). Одним из таких является среднее линейное отклонение. Этот показатель характеризует меру разброса значений вокруг их среднего. В чем суть? Для того, чтобы показать меру разброса данных, нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это среднее арифметическое. Далее нужно посчитать, насколько каждое значение отклоняется от средней. Нас интересует среднее из таких отклонений. Однако напрямую складывать положительные и отрицательные отклонения нельзя, т.к. они взаимоуничтожатся и их сумма будет равна нулю. Поэтому все отклонения берутся по модулю. Средне линейное отклонение рассчитывается по формуле:
где
a – среднее линейное отклонение,
X – анализируемый показатель,
X̅ – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Рассчитанное по этой формуле значение показывает среднее абсолютное отклонение от средней арифметической. Наглядная картинка в помощь.
Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.
Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор провести статистический анализ длины черенков. Отобрал 10 штук и замерил их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно, в среднем на 16 см. Есть, о чем поговорить с работниками.
На этом сегодняшнюю заметку закончим. В следующей статье будут рассмотрены такие показатели вариации, как дисперсия, среднеквадратичное отклонение и коэффициент вариации.
Поделиться в социальных сетях:
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Metod_labr.doc
Скачиваний:
4
Добавлен:
10.09.2019
Размер:
1.49 Mб
Скачать
-
Рассчитать среднее абсолютное линейное отклонение и относительное линейное отклонение.
Решение.
-
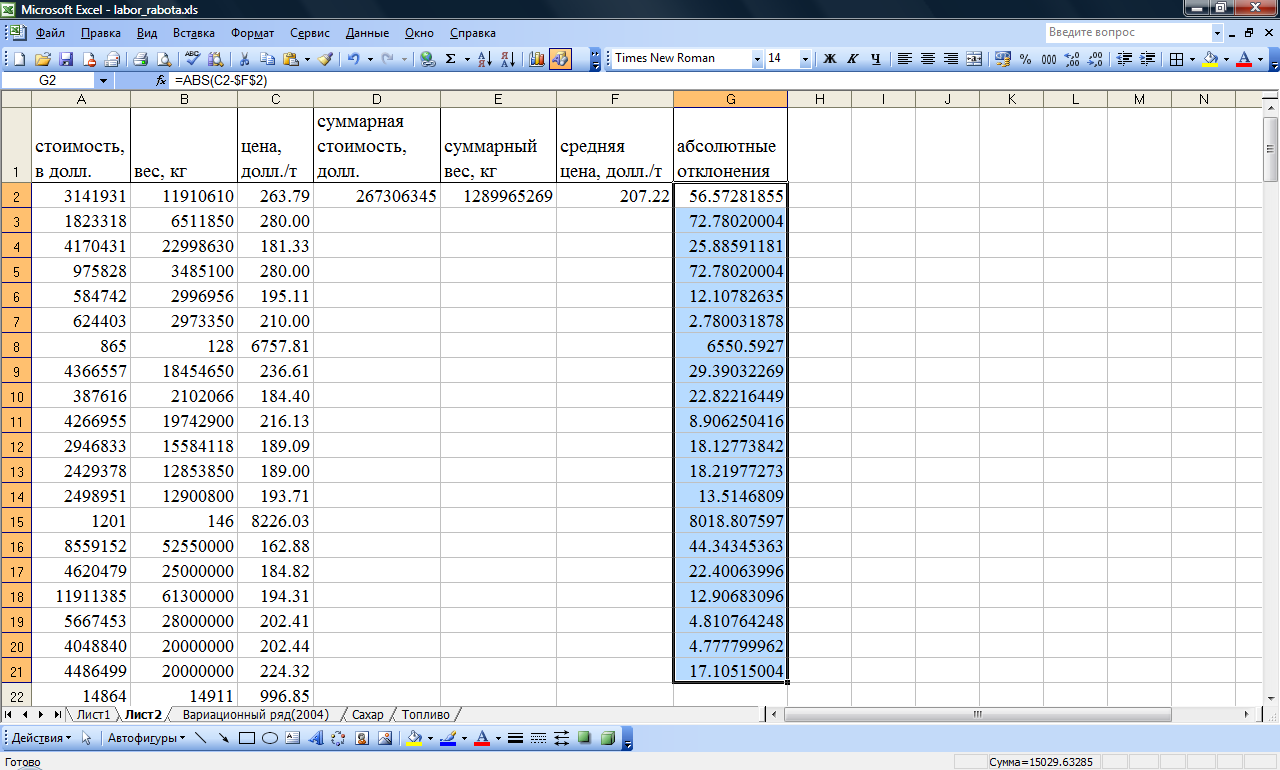
Рассчитать
столбец абсолютных отклонений от
средней цены, для этого воспользоваться
функцией ABS(*),
аргументом функции является разность
первой цены и средней цены. Ячейку со
средней ценой следует абсолютизировать
в формуле, нажав на функциональную
клавишу F4.
Затем скопировать формулу на весь
столбец. Пример представлен на Рис.10. -
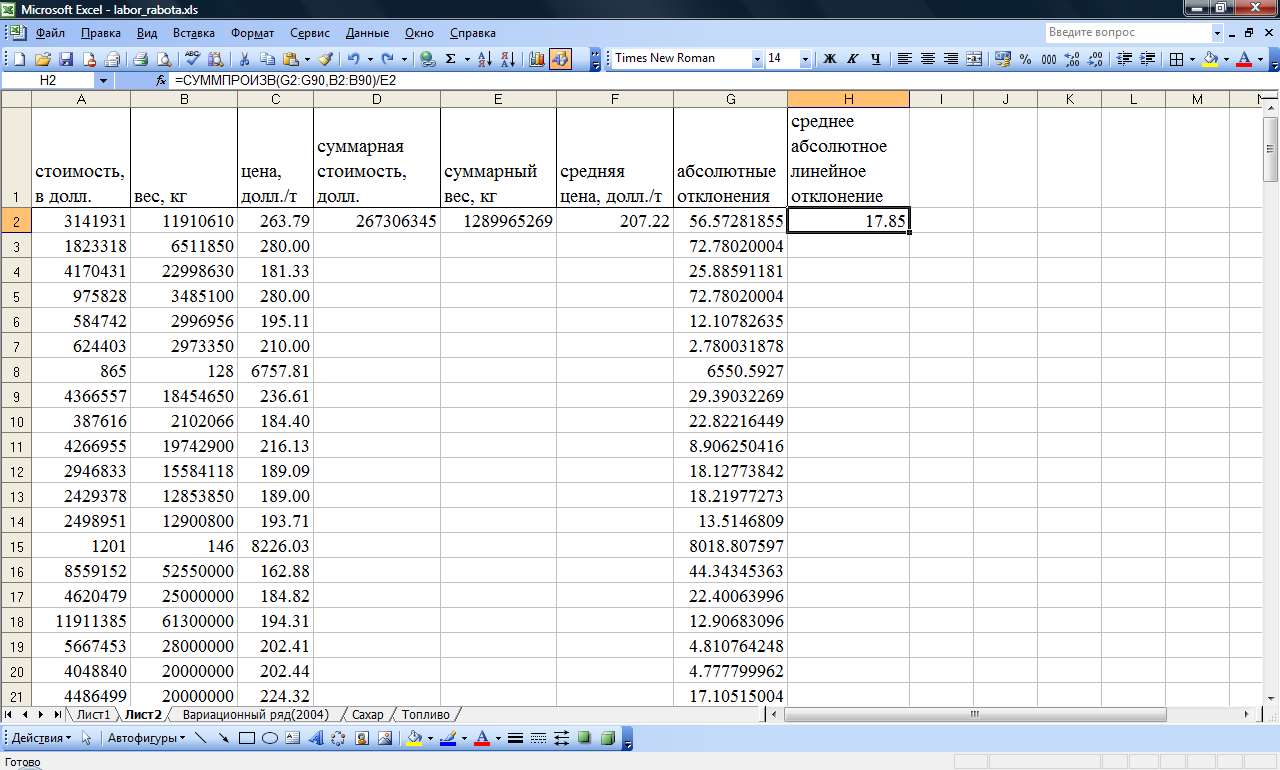
Рассчитать
среднее абсолютное линейное отклонение
по формуле: в числителе – функция
СУММПРОИЗВ(*;*)
(1 аргумент – массив абсолютных линейных
отклонений, 2 аргумент – массив весов);
в знаменателе – суммарный вес. Пример
представлен на Рис. 11. Функция
СУММПРОИЗВ(*;*)
– находится
в разделе Математические
функции и
вычисляет сумму попарных произведений
соответствующих элементов первого и
второго массивов-аргументов. -
Рассчитать
относительное линейное отклонение по
формуле: в числителе – среднее абсолютное
линейное отклонение; в знаменателе –
средняя цена; результат перевести в
проценты (в меню выбираем Формат
– Ячейки – Число – Процентный).
-
Рассчитать дисперсию, среднее
квадратическое отклонение и коэффициент
вариации.
Решение.
-
Рассчитать столбец
квадратов отклонения от средней цены.
Для этого можно возвести в квадрат
первое абсолютное отклонение (возведение
в степень осуществляется с помощью
знака «^»). Затем скопировать формулу
на весь столбец. -
Рассчитать
дисперсию по формуле: в числителе –
функция СУММПРОИЗВ(*;*)
(1 аргумент – массив квадратов отклонений,
2 аргумент – массив весов); в знаменателе
– суммарный вес. -
Рассчитать среднее
квадратическое отклонение, по формуле
дисперсия в степени 0,5. -
Рассчитать
коэффициент вариации по формуле: в
числителе – среднее квадратическое
отклонение; в знаменателе – средняя
цена; результат перевести в проценты.
Рис.10. Вычисление
абсолютных отклонений
Рис.11.
Вычисление среднего абсолютного
линейного отклонения
4. Практическая работа №4. «Статистическое изучение взаимосвязей»
Название
изучаемой темы по программе дисциплины:
«Статистическое
изучение взаимосвязей».
Учебные вопросы: Простая
корреляция и регрессия. Определение
формы и оценка параметров уравнения
регрессии. Метод наименьших квадратов.
Индекс корреляции и коэффициент линейной
корреляции. Построение корреляционной
матрицы.
Цели работы: научиться выполнять
в электронной таблице MS
Excel
-
вычисление
коэффициента линейной корреляции; -
построение
корреляционной матрицы; -
построения
корреляционного поля; -
построение
уравнения линейной регрессии.
Теоретический
материал:
Глава 16,
[2].
Типовые задания
-
Изучить
корреляционную связь между стоимостными
объёмами импорта 17
товарной группы,
оформленными различными таможнями
ЮТУ. Выбрать
две таможни с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между таможнями
на основе коэффициентов корреляции и
детерминации.
-
Изучить
корреляционную связь между физическими
объёмами импорта 17
товарной группы,
оформленными различными таможнями
ЮТУ. Выбрать
две таможни с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между таможнями
на основе коэффициентов корреляции и
детерминации.
-
Изучить
корреляционную связь между стоимостными
объёмами импорта 17
товарной группы,
оформленными в различных субъектах
ЮФО. Выбрать
два субъекта ЮФО с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между субъектами
на основе коэффициентов корреляции и
детерминации. -
Изучить
корреляционную связь между физическими
объёмами импорта 17
товарной группы,
оформленными в различных субъектах
ЮФО. Выбрать
два субъекта ЮФО с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между субъектами
на основе коэффициентов корреляции и
детерминации. -
Изучить
корреляционную связь между стоимостными
объёмами экспорта 27
товарной группы,
оформленными различными таможнями
ЮТУ. Выбрать
две таможни с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между таможнями
на основе коэффициентов корреляции и
детерминации.
-
Изучить
корреляционную связь между физическими
объёмами экспорта 27
товарной группы,
оформленными различными таможнями
ЮТУ. Выбрать
две таможни с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между таможнями
на основе коэффициентов корреляции и
детерминации. -
Изучить
корреляционную связь между стоимостными
объёмами экспорта 27
товарной группы,
оформленными в различных субъектах
ЮФО. Выбрать
два субъекта ЮФО с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между субъектами
на основе коэффициентов корреляции и
детерминации. -
Изучить
корреляционную связь между физическими
объёмами экспорта 27
товарной группы,
оформленными в различных субъектах
ЮФО. Выбрать
два субъекта ЮФО с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между субъектами
на основе коэффициентов корреляции и
детерминации.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.
Примеры методов анализа числовых рядов в Excel
Смысл данной функции становится предельно ясен после рассмотрения примера. Допустим, на протяжении суток каждые 3 часа фиксировались показатели температуры воздуха. Был получен следующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. С помощью функции СРЗНАЧ можно определить среднее значение температуры – 19,88 (округлим до 20). Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.
Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.
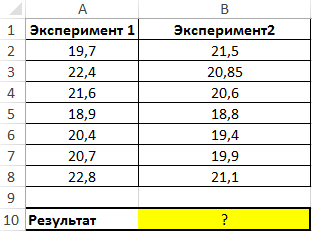
Пример 1. Имеются два ряда значений, представляющих собой результаты наблюдений одного и того же физического явления, сделанные в ходе двух различных экспериментов. Определить, среднее отклонение от среднего значения результатов для какого эксперимента является максимальным?
Вид таблицы данных:
Используем следующую формулу:
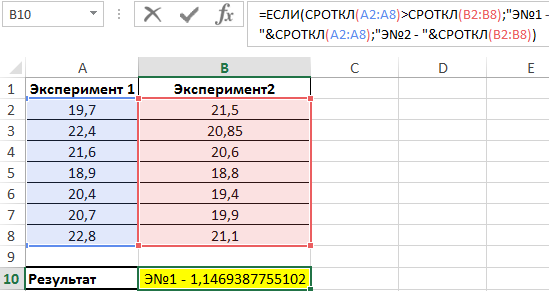
Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с использованием функции ЕСЛИ, возвращаем соответствующий результат.
Полученное значение:
В результате мы получили среднее отклонение от среднего значения. Это весьма интересная функция для технического анализа финансовых рынков, прогнозов курсов валют и даже позволяет повысить шансы выигрышей в лотереях.
Формула расчета линейного коэффициента вариации в Excel
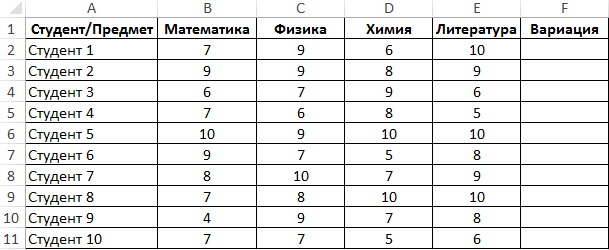
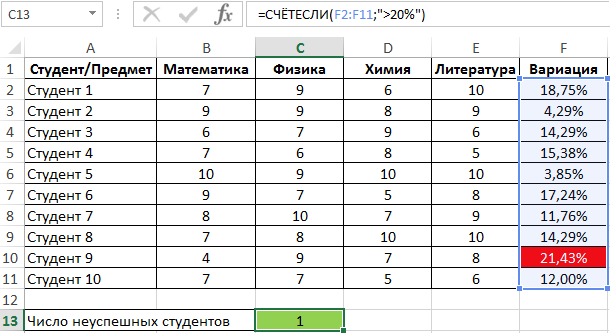
Пример 2. Студенты сдали экзамены по различным предметам. Определить число студентов, которые удовлетворяют следующему критерию успеваемости – линейный коэффициент вариации оценок не превышает 15%.
Вид таблицы данных:
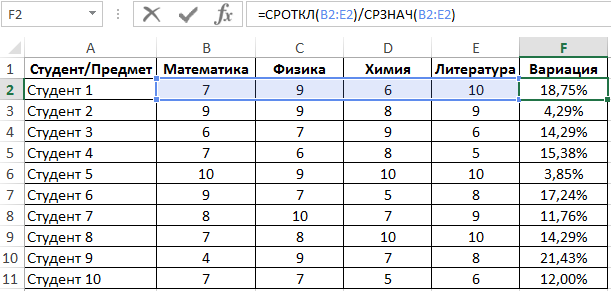
Линейный коэффициент вариации определяется как отношение среднего отклонения к среднему значению. Для расчета используем следующую формулу:
Растянем ее вниз по столбцу и получим следующие значения:
Для определения числа неуспешных студентов по указанному критерию используем функцию:
Полученный результат:
Правила использования функции СРОТКЛ в Excel
Функция имеет следующий синтаксис:
=СРОТКЛ(число1;[число2];…)
Описание аргументов:
- число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
- [число2];… – необязательный, принимает второе и последующие значения из исследуемого числового ряда.
Примечания:
- При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
- В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ({2;5;4;7;10}).
- Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
- Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
- Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
- Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.