Напряжение на конденсаторе
Что такое конденсатор
Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.
Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).
 Термин из учебного пособия
Термин из учебного пособия
Формула
Нахождение тока конденсаторного заряда происходит по формуле, представленной ниже. Измеряется он в фарадах, что равно кулону или вольту.
 Формула нахождения заряда конденсатора
Формула нахождения заряда конденсатора
В целомэто элемент электросети, накапливающий и сохраняющий напряжение в ней. Бывает разного типа и размера, к примеру, электролитическим, керамическим и танталовым. Состоит, в основном, из нескольких токопроводящих обкладок с диэлектриком. Его емкость зависит от размеров диэлектрика и заполнителя между обкладками. Заряжается благодаря электричеству. Определить ток конденсаторного заряда можно измерительными приборами и формулой.
формулы для конденсаторов
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
- В чем измеряется емкость конденсатора
- Формула энергии конденсатора
- Формула заряда конденсатора
- Формула тока утечки конденсатора
Измерение емкости конденсатора мультиметром и специальными приборами
Некоторые мультиметры имеют функцию измерения емкости. Взять хотя бы эти распространенные модели: M890D, AM-1083, DT9205A, UT139C и т.д. Также в продаже есть цифровые измерители емкости, например, XC6013L или A6013L.
Также в продаже есть цифровые измерители емкости, например, XC6013L или A6013L.
С помощью любого из этих приборов можно не только узнать точную емкость конденсатора, но и убедиться в отсутствии короткого замыкания между обкладками или внутреннего обрыва одного из выводов.
Некоторые производители даже уверяют, что их мультиметры способны проверить емкость конденсатора не выпаивая его с платы. Что, конечно же, противоречит здравому смыслу.
К сожалению, проверка конденсатора мультиметром не поможет определить такие наиважнейшие параметры, как ток утечки и эквивалентное последовательное сопротивление (ESR). Их измерить только с помощью специализированных тестеров. Например, с помощью весьма недорогого LC-метра.
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух 
Пусть заряды обкладок равны  и
и  . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина
. Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина  — заряд положительной обкладки — называется зарядом конденсатора.
— заряд положительной обкладки — называется зарядом конденсатора.
Пусть  — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
— площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

Здесь  — напряжённость поля положительной обкладки,
— напряжённость поля положительной обкладки,  — напряженность поля отрицательной обкладки,
— напряженность поля отрицательной обкладки,  — поверхностная плотность зарядов на обкладке:
— поверхностная плотность зарядов на обкладке:

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля  имеем:
имеем:

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

 (4)
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4) . Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно  . Поскольку поле внутри конденсатора является однородным, разность потенциалов
. Поскольку поле внутри конденсатора является однородным, разность потенциалов  между обкладками равна произведению
между обкладками равна произведению  на
на  (вспомните связь напряжения и напряжённости в однородном поле!):
(вспомните связь напряжения и напряжённости в однородном поле!):
 (5)
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
 (6)
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на  В. Формула (6) , таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
В. Формула (6) , таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
 (7)
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними. Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью  . Как изменится ёмкость конденсатора?
. Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в  раз, так что вместо формулы (4) теперь имеем:
раз, так что вместо формулы (4) теперь имеем:
 (8)
(8)
Соответственно, напряжение на конденсаторе:
 (9)
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
 (10)
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10) : заполнение конденсатора диэлектриком увеличивает его ёмкость.
Полярные и неполярные конденсаторы
Очень важным является разделение конденсаторов на полярные и неполярные.
Приборы на основе оксидов: электролитические алюминиевые и танталовые обычно являются полярными, а значит если перепутать их полярность — они выйдут из строя. Причём этот выход из строя будет сопровождаться бурной электрохимической реакций вплоть до взрыва конденсатора.

На полярных конденсаторах всегда имеется маркировка. Как правило на электролитических конденсаторах на корпусе контрастной полосой отмечается отрицательный вывод (катод), у танталовых (в желтых прямоугольных корпусах) полоской помечается положительный вывод (анод). Если есть сомнения в маркировке, то лучше найти документацию на этот конденсатор и убедиться.
Неполярные же конденсаторы можно включать в цепь какой угодно стороной. К примеру, многослойные керамические конденсаторы — неполярные.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Определение емкости неизвестного конденсатора
Способ : измерение емкости специальными приборами
Самый просто способ — измерить емкость с помощью прибора, имеющего функцию измерения емкостей. Это и так понятно, и об этом уже говорилсь в начале статьи и тут нечего больше добавить. Если с приборами совсем туган, можно попробовать собрать простенький самодельный тестер. В интернете можно найти неплохие схемы (посложнее, попроще, совсем простая).
Если с приборами совсем туган, можно попробовать собрать простенький самодельный тестер. В интернете можно найти неплохие схемы (посложнее, попроще, совсем простая).
Ну или раскошелиться, наконец, на универсальный тестер, который измеряет емкость до 100000 мкФ, ESR, сопротивление, индуктивность, позволяет проверять диоды и измерять параметры транзисторов. Сколько раз он меня выручал!
Относительная диэлектрическая проницаемость
Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.
Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.
Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.
Порошки оксидов металлов – от 6 до 20
Формулы измерения напряжения конденсаторов
Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.
Вам это будет интересно Как выбрать цветовую температуру
 Основные формулы для расчета
Основные формулы для расчета
В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.
Источник
Мы уже говорили о том, что вокруг любого заряженного тела существует электрическое поле. Также, мы знаем, что создав электрическое поле, можно упорядочить движение заряженных частиц, тем самым, получив электрический ток. Но кроме этого, существует возможность накапливать заряды и, соответственно, энергию электрического поля. Если мы сможем сосредоточить положительные заряды на одном полюсе, а отрицательные на другом — то мы получим электрическое поле. Если такие полюса соединить проводником, то в этом проводнике возникнет электрический ток.
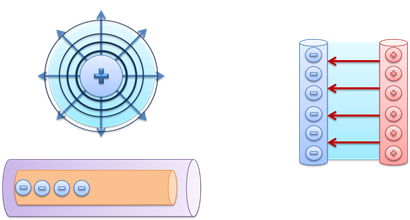
Если же, напротив, изолировать эти полюса друг от друга с помощью диэлектрика, то мы сможем продолжать накапливать заряды, тем самым увеличивая силу электрического поля. Устройство, позволяющее осуществить это технически, называется конденсатором.

В простейшем конденсаторе в качестве полюсов используются две одинаковые металлические пластины (которые называются обкладками), а качестве диэлектрика — воздух (или бумага). Толщина диэлектрика должна быть небольшой по сравнению с размерами обкладок.
В качестве опыта сделаем следующее: зарядим пластины конденсатора с помощью источника тока.

После того, как на пластинах конденсатора сосредоточатся заряды с противоположным знаком, мы выключим источник тока. Несмотря на это, между пластинами будет существовать электрическое поле, и если мы соединим пластины проводником, то по нему пройдет ток. Значит, заряженный конденсатор сам является источником тока.
Как мы помним, ток не будет проходить через проводник при отсутствии электрического поля. Также, мы знаем, что чем больше заряд, тем больше его электрическое поле, а электрическое поле имеет такую характеристику, как напряжение. Напомним, что напряжение характеризует отношение работы электрического поля по переносу заряда к величине этого заряда:
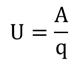
Проводя многочисленные опыты, ученые выяснили, что для одного и того же конденсатора отношение заряда к электрическому напряжению остается неизменно:
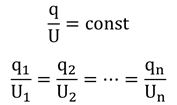
Электрическое напряжение между обкладками конденсатора увеличивается ровно во столько раз, во сколько увеличивается количество заряда, сосредоточенного на пластинах.
Но у разных конденсаторов соотношение заряда и напряжения было различным, из чего можно сделать вывод, что мы имеем дело со свойством самого конденсатора. Это свойство назвали электроёмкостью, хотя иногда вместо слова «электроёмкость» употребляют просто слово «ёмкость»:
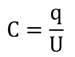
Единицей измерения электроёмкости является фарад, в честь Майкла Фарадея:
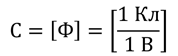

1 Ф
1 Ф — это очень большая ёмкость для конденсатора. Чаще всего конденсаторы имеют электроёмкость порядка одного мкФ или нФ.
Надо сказать, что конденсатор, как и любое заряженное тело, обладает определенной энергией. Ведь, чтобы разделить положительные и отрицательные заряды для зарядки конденсатора, нужно совершить работу. Эта работа и будет равна энергии конденсатора, исходя из закона сохранения энергии:
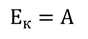
Как мы помним, работа электрического поля равна
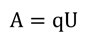
Но дело в том, что в процессе разрядки конденсатора напряжение не постоянно, поэтому для расчетов следует использовать среднее напряжение:
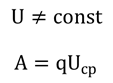
Для нахождения среднего напряжения используется довольно сложная математическая функция, которую мы не будем рассматривать на данном этапе, и просто примем, так сказать, на веру, формулу по которой рассчитывается энергия конденсатора:
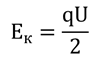
В этой формуле мы можем вместо количества заряда подставить произведение напряжения и электроёмкости. Тогда получим, что энергия конденсатора прямо пропорциональна электроёмкости и квадрату напряжения между пластинами:
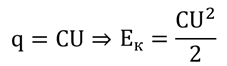
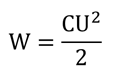
Несмотря на то, что конденсаторы могут достаточно долго накапливать энергию, отдают они эту энергию очень быстро. Это свойство конденсаторов широко используется людьми. Почти в любой аппаратуре есть конденсаторы. Например, в радиоэлектронике конденсаторы используются для того, чтобы настраиваться на ту или иную частоту. Только там используются конденсаторы с переменной электроёмкостью. Дело в том, что ёмкость конденсатора зависит от площади пластин.

Вращая подвижную часть такого конденсатора, мы можем изменять площадь пластин и, таким образом, электроёмкость. Более подробно такие конденсаторы будут изучены позже.
Упражнения.
Задача 1. При напряжении 220 В, заряд на конденсаторе составляет 30 мкКл. Какова электроёмкость этого конденсатора?

Задача 2. Конденсатор накопил заряд, равный 300 мкКл. Какая на это была затрачена энергия, если ёмкость конденсатора составляет 1 мкФ?
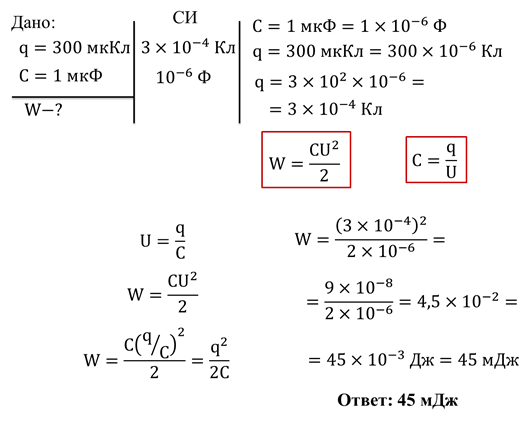
Задача 3. К заряженному конденсатору с электроёмкостью 0,1 мФ подключили лампочку. По ней прошел ток силой 20 мА, а через 2 с лампочка погасла. Какое напряжение было изначально между пластинами конденсатора?
Давайте подумаем, что именно произошло? Конденсатор накопил заряд, а как только его включили в цепь, он начал разряжаться и был источником тока. Когда конденсатор разрядился, лампочка погасла, потому что через неё перестал проходить ток. Значит, на разрядку конденсатора ушло 2 секунды.

В общем, теоретически, мы всё правильно решили, но на самом деле, эта задача немного упрощённая, потому что в действительности ток бы уменьшался по мере разрядки конденсатора. Но это пока слишком сложные расчёты, мы потом научимся, как их делать.
Домашняя работа
Стр. 151 — 156
Упр. 38
ТОЭ › Расчет цепей синусоидального тока

При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости, через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток).Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.
Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.
Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(P = 0).
Что такое конденсатор
Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.

Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).

Схема замещения конденсатора с последовательным соединением элементов
Реальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Хс сопротивлениями. На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13. 18,6). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным. Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью С Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а. Если вам интересно прочитайте статью о настоящих конденсаторах которые применяются в промышленности.
Характеристики конденсаторов
Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.
Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.

Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.
В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.
Вам это будет интересно Особенности расчета мощности по току и напряжению
Треугольник проводимостей для конденсатора
Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная G = IG/U и емкостная Вс = Iс/U проводимости, а гипотенузой — полная проводимость цепи Y = I/U. Из треугольника проводимостей
Связь между действующими величинами напряжения и тока выражается формулами
I = UY
U = I/Y (13.35)
Из треугольников токов и проводимостей определяют величины
cosφ = IG/I = G/Y; sinφ = Ic/I = Bc/Y; tgφ = IC/IG = Bc/G. (13.36)
В чем измеряется напряжение конденсаторов
Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.

Мощность цепи с конденсатором
Выражение мгновенной мощности реального конденсатора
p = ui = Umsinωt * Imsin(ωt+φ)
совпадает с выражением мгновенной мощности катушки. Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17. Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19) — (13.22)]. Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U. В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности; активная
P = UIG = UIcosφ
реактивная
Q = UIC = UIsinφ
полная
Что влияет на напряжение конденсаторов
Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд. Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.
Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.

Схема замещения конденсатора с параллельным соединением элементов
Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной Bс проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе G = Р/Uc2, а емкость — конструкцией конденсатора. Предположим, что проводимости G и Вс для такой цепи известны, а напряжение имеет уравнение
u = Umsinωt.
Требуется определить токи в цепи и мощность. Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них так же синусоидальны. При параллельном соединении ветвей G и Вс , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:
i = iG + ic, (13.30)
Учитывая, что ток iG совпадает по фазе с напряжением, а ток ic опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:

Как вычислить напряжение и вольтаж
Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.
Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.

Устройство конденсатора
Конденсатор представляет собой две проводящие поверхности, разделённые слоем диэлектрика. Как правило, эти поверхности делаются из тонкой медной или алюминиевой фольги, иногда свёрнутой в рулон. В качестве диэлектрика применяется бумага, керамика, некоторые виды пластмасс. От каждой из проводящих поверхностей (они называются обкладками) выводится электрический контакт — клемма. Вся конструкция помещается в корпус, обеспечивающий механическую прочность.

Формулы измерения напряжения конденсаторов
Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.
Вам это будет интересно Обозначение разного электрооборудованья на схемах

В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.
Векторная диаграмма токов в цепи с конденсатором
Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению
I = IG + IC
Действующие величины составляющих тока:
IG = GU (13.31)
IC = BCU (13.32)
Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φa =0). Вектор IG совпадает по направлению с вектором U, а вектор IC направлен перпендикулярно вектору U с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90º. Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC :

i = Imsin(ωt + φ)
Переменный ток
Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока
. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.
Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем). Заряженный конденсатор для постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен резистору с некоторым вполне определенным сопротивлением (если пока забить забыть про всякие там сдвиги фазы, об этом ниже). Нам надо каким-нибудь образом получить связь между током и напряжением на конденсаторе.
Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор. Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.
Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение
Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt. Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.
Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением
Давайте-ка выразим из этой формулы заряд конденсатора:
А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:
Емкость конденсатора у нас является величиной постоянной
. Она определяется
исключительно самим конденсатором
, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость
С
конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением
U
нельзя так поступить!
Напряжение на конденсаторе будет изменяться со временем. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него. Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.
А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:
По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.

Рисунок 1 – Поясняющая картинка
На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.
Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения.
Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения
U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.
Пусть напряжение на конденсаторе емкостью C
изменяется по закону синуса вот таким вот образом
Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше. Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную
Или можно записать вот так
Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то . Не понятно, откуда взялось это выражение? Погуглите формулы приведения
. Штука полезная, знать не помешает. А еще лучше, если вы хорошо знакомы с
тригонометрическим кругом
, на нем все это видно очень наглядно.
Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок. Итак, сейчас мы получили немаловажный вывод – если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов.
Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости
C
конденсатора, амплитуды приложенного к нему напряжения
U
m и частоты
ω
. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).

Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе
На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе. По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).
Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t)
через конденсатор емкостью
C
. И закон этот пусть тоже будет синусоидальным
Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:
По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом
Здесь мы снова воспользовались интересными сведениями из тригонометрии, что . И снова формулы приведения
придут вам на помощь, если не понятно, почему получилось именно так.
Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов. Более того, они не просто так сдвинуты. Ток опережает
напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.
Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.
Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.
Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем.
Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.
Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.
Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото )

Рисунок 3 – Ищем ток через этот конденсатор
Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.
Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное
значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону
Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так
Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока
Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало. Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует . Однако на этом принципе возможно изготовление так называемых источников питания с гасящим конденсатором. Ну да это тема для отдельной статьи и здесь мы не будем ее затрагивать.
Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.

Рисунок 4 – График напряжения в розетке

Рисунок 5 – График тока через конденсатор
Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть. И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla
Нет конденсатора нужного номинала: что делать
Очень часто начинающие домашние мастера, обнаружив поломку прибора, стараются самостоятельно обнаружить причину. Увидев сгоревшую деталь, они стараются найти подобную, а если это не удаётся, несут прибор в ремонт. На самом деле, не обязательно, чтобы показатели совпадали. Можно использовать конденсаторы меньшего номинала, соединив их в цепь. Главное – сделать это правильно. При этом достигается сразу 3 цели – поломка устранена, приобретён опыт, сэкономлены средства семейного бюджета.
Попробуем разобраться, какие способы соединения существуют и на какие задачи рассчитаны последовательное и параллельное соединение конденсаторов. Часто без соединения конденсаторов в батарею не обойтись. Главное – сделать это правильно
Действие конденсатора
Казалось бы, с точки зрения электрического тока конденсатор представляет собой разрыв цепи. Однако это не совсем так. Если создать на одной из обкладок конденсатора избыток свободных носителей электрического заряда, то свободные носители такого же знака начнут уходить с другой обкладки, а носители противоположного знака — наоборот, собираться на ней. То есть и на другой обкладке носители придут в движение.
Получается, что конденсатор не является полным разрывом электрической цепи. Если изменения заряда на первой обкладке производить попеременно, то в одну, то в другую сторону (подав на обкладку переменный ток) — то на второй обкладке заряды также будут попеременно двигаться.
Конденсатор способен передавать переменный ток, а также любые изменения тока вообще. Он является разрывом цепи только для постоянного тока.
Как проверить качество соединения конденсаторов в цепи
Самый идеальный случай, когда у нас на руках имеется соответствующего типа вольтметр. Он стоит в пределах одной тысячи рублей.
Это не так много, учитывая, что вкупе мы получаем прибор для измерения сопротивлений, постоянного и переменного напряжения, токов.
Гнездо под измерение конденсатор (см. фото слева) представляет собой две узкие щели, куда должны вставляться ножки.
По нашим наблюдениям нет разницы, какой стороной вставлять электролитический конденсатор. Хотя лучше все же руководствоваться инструкцией по эксплуатации.
Ззатем как-то нужно промаркировать их, либо разложить по нарисованной на бумаге схеме, где уже проставлять все цифры (кстати, так обычно и делается во всей китайской технике).
Затем следует вычислить по формулам, какое именно значение должно получиться и проверить это тестером. Не получается? Значит, качество контактов плохое – меньше применяйте скруток.
СОЕДИНЕНИЯ КОНДЕНСАТОРОВ
Если необходимо увеличить общую емкость конденсаторов, то их соединяют между собой параллельно (рис. 9, а
). При этом способе соединения общая площадь пластин увеличивается по сравнению с площадью пластины каждого конденсатора. Общая емкость конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов и вычисляется по формуле Собщ=С1 + С2+С3+
(10)
Это можно подтвердить следующим образом.
Соединенные параллельно конденсаторы находятся под одним и тем же напряжением, равным U вольт, а общий заряд этих конденсаторов равен q кулонов. При этом каждый конденсатор соответственно получает заряд q 1 , q 2 , q 3, и т. д. Следовательно,
q общ = q 1 + q 2 + q 3 +
Из формулы (8) вытекает, что заряд
q общ = С общ U (11)
а заряды q 1 = С 1 U; q 2 = С 2 U; q 3 = С 3 U.
Подставив эти выражения в формулу (11), получим:
С общ U= С 1 U + С 2 U + С 3 U.
Разделив левую и правую части этого равенства на равную для всех конденсаторов величину U, после сокращения найдем:
С общ = С 1 + С 2 + С 3
Пример
. Три конденсатора емкостью С 1 =2 мкф ; C 2 =0,1 мкф и C 3 =0,5 мкф соединены параллельно.
Вычислить их общую емкость.
С общ = С 1 + С 2 + С 3 =2+00,1+0,5=2,6 мкф.
Общую емкость конденсаторов, имеющих одинаковую емкость и соединенных параллельно, можно вычислить по формуле
С общ = Сn, (12)
где С — емкость одного конденсатора,
n — число конденсаторов.
Пример.
Пять конденсаторов емкостью 2 мкф каждый соединены параллельно. Определить их общую емкость.
С общ = Сn =2·5=10 мкф.
Конденсаторы соединяют последовательно (рис. 9, б), когда рабочее напряжение установки превышает напряжение, на которое рассчитана изоляция одного конденсатора. В этом случае правую пластину первого конденсатора соединяют с левой пластиной второго, правую пластину второго — с левой пластиной третьего и т. д. Общая емкость конденсаторов при таком соединении уменьшается. Величина, обратная общей емкости конденсаторов, соединенных последовательно , равна сумме обратных величин емкостей отдельных конденсаторов:
Это можно подтвердить следующим образом. Общее напряжение на конденсаторах U общ а на каждом конденсаторе U 1 , U 2 , U 3 , тогда
U общ = U 1 +U 2 + U 3 .
Из Формулы (8) следует, что напряжение
U общ = (14)
а напряжение
Подставив эти выражения в формулу (14), получим:
Разделим левую и правую части этого равенства на величину q и после сокращения найдем:
Пример. Три конденсатора С1=2 мкф, С2=4 мкф и С3=8 мкф соединены последовательно. Определить их общую емкость.
Если последовательно соединены конденсаторы, имеющие одинаковую емкость, то их общую емкость можно вычислить по формуле
Пример.
Четыре конденсатора емкостью 1000 пф каждый соединены последовательно. Определить их общую емкость. Решение.
Если последовательно соединены два конденсатора различной емкости, то их общую емкость можно найти по формуле
Пример.
Два конденсатора С 1 =200 пф
и С 2 =300 пф соединены последовательно. Вычислить их общую емкость.
Как видно из приведенных примеров, общая емкость конденсаторов, соединенных последовательно, всегда меньше наименьшей емкости, входящей в соединение.
Конденсаторы выбирают по емкости и рабочему напряжению которое подается на его пластины при включении в схему. При напряжении, превышающем допустимое, происходит пробой диэлектрика в конденсаторе. Это напряжение называется пробивным. Пробой диэлектрика сопровождается электрическим разрядом — искрой с характерным треском. Конденсатор с пробитым диэлектриком не пригоден для применения.
Каждый диэлектрик обладает определенной электрической прочностью, т. е. способностью противостоять пробою. Электрическая прочность (табл. 2) измеряется обычно в (в/см
) и определяется по формуле
где U — напряжение, в
d — толщина диэлектрика, см.
Многие, собирая тот или иной прибор, часто задумываются о том, как соединить конденсаторы параллельным или последовательным соединением. Далеко не каждый номинал выпускается промышленностью, поэтому задача обеспечить конструкцию связкой ёмкостей встречается тут и там. При параллельном включении номиналы складываются, а при последовательном используется более сложная формула. А ещё конденсаторы бывают подстроечными, такие совершенно точно включаются в цепи, где требуется обеспечить нужные резонансные характеристики. В этом случае также требуется решить указанную выше задачу. Проблема ещё в том, что часто сборка какого-нибудь индукционного нагревателя идёт буквально на коленках, железа целая кипа, колодок под рукой нет, а паять лень – что делать?
Что такое конденсатор
Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.

Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).

Полярность конденсатора
Полярность: некоторые конденсаторы изготавливаются таким образом, что они могут выдерживать приложенное напряжение только одной полярности, но не другой. Это связано с их конструкцией: диэлектрик представляет собой микроскопически тонкий слой изоляции, нанесенный во время изготовления на одну из пластин с помощью постоянного напряжения. Они называются электролитическими конденсаторами, и их полярность четко обозначена.

Изменение полярности напряжения на электролитическом конденсаторе может привести к разрушению этого сверхтонкого диэлектрического слоя, что приведет к разрушению устройства. Однако толщина этого диэлектрика позволяет получать чрезвычайно высокие значения емкости при относительно небольшом размере корпуса. По той же причине электролитические конденсаторы имеют тенденцию иметь низкое номинальное напряжение по сравнению с другими типами конструкций конденсаторов.
Характеристики конденсаторов
Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.
Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.

Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.
В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.
Вам это будет интересно Формулировка и определение закона Ома
Схемы на все случаи жизни
Под номинальным напряжением конденсатора понимается предельно допустимое напряжение постоянного тока (или сумма напряжений постоянного и переменного токов), при котором конденсатор может работать в течение гарантируемого срока службы при максимально допустимой рабочей температуре.
Номинальное напряжение постоянного тока устанавливается с необходимым запасом по отношению к длительной электрической прочности диэлектрика, исключающим возникновение в течение гарантируемого срока службы сильного старения конденсатора, вызывающего существенное ухудшение его электрических характеристик.
Допускаемые значения амплитуды переменного тока выбираются таким образом, чтобы исключить возможность развития ионизации в конденсаторе и его нагрев сверх допускаемой предельной температуры.
Эти значения обычно приводятся в технических условиях на конденсатор. При эксплуатации конденсаторов на переменном или постоянном с переменной составляющей напряжениях следует придерживаться следующих правил:
• Сумма постоянной составляющей и амплитуды пульсации не должна превышать номинального рабочего напряжения.
• Амплитуда переменного напряжения не должна превышать величины, определяемой формулой: U=400*103*√(Pp/fC), где U — амплитуда переменного напряжения,В; Pp — допустимая реактивная мощность, Вар; С — емкость, пф; f — частота, гц.
• Ток, проходящий через конденсатор, не должен превышать допустимой по ТУ величины. Максимальным значением допустимого переменного напряжения, равным номинальному, обладают керамические низковольтные высокочастотные конденсаторы. Ограничение напряжения для этих конденсаторов обусловливается допустимыми значениями реактивной мощности и тока.
Для слюдяных конденсаторов допустимое значение амплитуды переменного напряжения в процентах от номинального в соответствии с действующими ТУ приведено ниже. Для конденсаторов типов КСО, СГМ: • На номинальные напряжения до 500 В: 100% до 500 гц, 60% от 500 до 10000 гц, 20% более 10000 гц;
• На номинальные напряжения 500 В: 50% до 500 гц, 30% от 500 до 10000 гц, 10% более 10000 гц;
• На номинальные напряжения от 1000 до 3000 в: 30% до 50 гц, 20% от 500 до 10000 гц, 5% более 10000 гц;
• На номинальные напряжения 5000 в и выше: 15% до 500 гц, 20% от 500 до 10000 гц, 3% более 10000 гц.
Срок службы конденсаторов зависит от приложенного напряжения и окружающей температуры. Следовательно, существует принципиальная возможность в зависимости от времени, в течение которого будет эксплуатироваться конденсатор, и окружающей температуры устанавливать допустимые значения рабочих напряжений, значительно отличающиеся от номинальных. Это обстоятельство, расширяющее возможность применения конденсаторов, использовано в некоторых металлобумажных конденсаторах.
Во избежание повреждения конденсатора нельзя допускать, чтобы амплитудное значение переменной составляющей (любой формы, частоты и длительности воздействия) превышало величину приложенного постоянного напряжения, так как при этом на аноде периодически будет создаваться отрицательный потенциал.
Величина допускаемого значения переменной составляющей для электролитических конденсаторов зависит от типа конденсатора и уменьшается пропорционально частоте.
Некоторые типы конденсаторов нежелательно использовать при напряжениях, значительно ниже номинального (особенно ниже 1 в), так как могут возникнуть нарушения в работе схем из-за неустойчивости внутренних контактов между обкладками и выводами, роста потерь и развития окислительных процессов, приводящих к временной или постоянной потери емкости. Примером таких конденсаторов являются конденсаторы типа БМ-1.
При низких напряжениях наиболее надежными являются конденсаторы с припаянными или приваренными, контактами: керамические, стеклоэмалевые, стеклокерамические, бумажные (БМ-2, БМТ-2, К40У-9), металлобумажные (МБГ, МБГТ, МБМ, К42У-2), металлопленочные (МПГ, МПГО, К71П-2Б), фторопластовые (К72П-6).
Для отбраковки конденсаторов с заведомо низкой электрической прочностью, обусловленной грубыми случайными дефектами, заводы-изготовители проверяют конденсаторы испытательным напряжением, значительно превышающим номинальное. Конденсаторы должны выдерживать воздействие испытательного напряжения в течение короткого времени (обычно 10 сек) не пробиваясь.
Обычно испытательное напряжение выбирается, исходя из запаса кратковременной электрической прочности конденсатора.
Для слюдяных конденсаторов испытательное напряжение выбирается обычно в два раза больше номинального, для бумажных на напряжение до 1500 в 3 раза больше, а при 1500 в и выше в 2 раза больше.
Испытательным напряжением на заводах-изготовителях обычно проверяются все выпускаемые конденсаторы (испытание на электрическую прочность), что позволяет отбраковывать образцы с особо грубыми дефектами, но, однако, не обеспечивает безотказность при последующей эксплуатации конденсаторов, выдержавших это испытание. У конденсаторов, истинное пробивное напряжение которых превышало испытательное на сравнительно небольшую величину, воздействие испытательного напряжения может вызвать необратимое изменение в диэлектрике, снижающее запас электрической прочности.
При повторном испытании на электрическую прочность, такие конденсаторы могут выйти из строя. Эксперименты показывают, что если достаточно большую партию конденсаторов неоднократно испытывать одним и тем же испытательным напряжением, то при последующих испытаниях всегда будет иметься некоторое количество пробитых образцов.
Исходя из сказанного, проверки конденсаторов на электрическую прочность следует стремиться уменьшать до предела, например до двух: 1) на заводе-изготовителе конденсаторов и 2) при входном контроле на заводе-потребителе.
Однако при входном контроле рекомендуется проводить испытание конденсаторов всех типов на кратковременную электрическую прочность при испытательном напряжении не выше 1.15*Uном.
Список использованной литературы
- Элементы радиоэлектронной аппаратуры. Электрические конденсаторы постоянной ёмкости. В.Н. Гусев, В.Ф.Смирнов. — М.: Советское радио, 1968.
В чем измеряется напряжение конденсаторов
Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.

Что влияет на напряжение конденсаторов
Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд. Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.
Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.

Немного конденсаторов и как они влияют на уровень пульсаций преобразователя
Как-то купил я некоторое количество разных радиокомпонентов в нашем местном магазине. И среди всего прочего там были и электролитические конденсаторы разных типов, которые мне понадобились для небольшой доработки одного из преобразователей и сегодня я расскажу о том, как простая замена конденсатора может сильно изменить характеристики преобразователя, ну или блока питания. Обзор сегодня будет короткий, собственно о конденсаторах вряд ли возможно долго рассказывать, но думаю что все таки и в таком виде он будет полезен. И да, в какой-то степени у меня сегодня «юбилейный», шестисотый обзор на муське.
Плату преобразователя, для которой я их планирую использовать, вы уже видели в одном из моих обзоров, а так как я все таки хочу ее применить по назначению, то решил немного доработать, для чего и были куплены конденсаторы.

Всего было куплено пять видов конденсаторов, двух производителей и с несколькими вариантами рабочего напряжения и емкости. Покупались в харьковском магазине Космодром вместе с кучей другой мелочевки.

Сначала мои любимые конденсаторы фирмы Samwha серии RD, в данном случае это 330мкФ 63 Вольта, стоят примерно по 20 центов, собственно потому что они недорогие и вполне качественные, я их часто и использую.

Следует отметить, что данные конденсаторы не относятся к низкоимпедансным и являются просто высокотемпературным вариантом более привычных SD, но тем не менее очень неплохо работают и в импульсных блоках питания.

Дальше все измеренные параметры будут идти в одном и том же порядке для всех конденсаторов и сюда входит: 1. Фото выштамповки на верхней крышке и форма изолятора 2. Вес, в данном случае двух конденсаторов, т.е. результат надо делить на 2. 3, 4. Габаритные размеры.
Зачем это надо. Конденсаторы очень часто подделывают и чтобы хот как-то иметь представление о виде оригинальных конденсаторов, нужен какой-то образец и в данном случае можно будет сравнивать купленные в других местах с данными фото.

Параметры обоих конденсаторов на частоте 100 Гц и 7.8 кГц.

Тоже Samwha, но уже другой серии, WL. Емкость 1000мкФ, напряжение 35 Вольт. Стоят примерно те же 20 центов — ссылка.

Данные конденсаторы уже относятся к низкоимпедансным, а значит их уже на «законном основании» можно применять в преобразователях и импульсных БП, они уже фигурировали у меня в обзоре доработки светильников.

Форма изолятора, выштамповка и габаритные размеры. Конденсаторы довольно габаритные.

Емкость, ESR.

А вот дальше пойдут конденсаторы фирмы Panasonic и начну с самого компактного из обозреваемых — 470мкФ 35 Вольт. Стоят они конечно уже подороже, примерно по 30-35 центов — ссылка.

Это также низкоимпедансные конденсаторы, о чем и заявлено в даташите.

Выштамповка верхней крышки имеет своеобразную форму, хотя изолятор очень похож Samwha.

Помимо неплохих характеристик отмечу любопытный факт, если посмотреть на фото, то видно что у Samwha маркировка расположена так, что плюс будет справа (если смотреть выводами вниз), а у Panasonic наоборот, плюс получается слева.

Тоже Panasonic, той же серии, на те же 35 Вольт, но уже с емкостью 820мкФ, стоят уже по 80 центов — ссылка.

Выштамповка на крышке такая же как у предыдущих, а вот форма изолятора заметно отличается.

Параметры просто класс, рекомендую однозначно. В даташите параметры приведены для частоты 100кГц, но мой измеритель так не умеет 

И третий Панасоник, выглядит немного по другому, цвет маркировки золотистый и есть логотип «М». Стоят чуть больше одного доллара за штучку — ссылка.

Форма выштамповки и изолятора точно такая же как у предыдущих, отличие только в самой маркировке.

Если сравнивать с Samwha RD, то здесь параметры конечно заметно лучше, но и разница в цене существенная.

Переделка проста и незамысловата, выпаиваем родные конденсаторы, ставим новые. Изначально стоял китайский «Sanyo» 470мкФ 50 Вольт. Из показанных выше пяти типов я выбрал два, на вход Samwha RD 330х63, на выход Panasonic 330х50. Изначально думал поставить на вход 330х50, а на выход пару 470х35 или один 820х35, но решил перестраховаться так как по входу будет около 48-50 Вольт и снижать его не хочется, а по выходу 35 были бы впритык. Samwha WL оказался слишком большим, еле влазил и я не стал его применять. Вообще выбор конденсаторов небольшого диаметра на 50-63 Вольта и емкостью 330мкФ и выше очень мал, хотелось что-то более емкое и желательно качественное с низким ESR, но увы…

Можно было бы конечно этим и ограничится, но мне очень было любопытно, есть ли разница в итоге и если есть, то какая, потому я сначала подключил плату с родными конденсаторами, измерил пульсации на выходе, а потом заменил конденсаторы и провел тот же тест в тех же условиях. Входное напряжение везде около 22 вольт, выходное: 1. 3.3 вольта 8 ампер 2. 6 вольт 8 ампер 3. 15 вольт 3.5 ампера.
Слева до переделки, справа соответственно после, хотя думаю что вы и так догадались «кто есть кто» 

А это измерения родных конденсаторов, самого плохого и самого хорошего, параметры третьего находятся где-то посередине. Если коротко, то примерно как у обычных конденсаторов, например Samwha стандартной серии на 85 градусов, но вот насчет долговечности у меня есть некоторые сомнения, думаю Samwha все таки будет надежнее.

И так, могу сказать что результат есть, причем очень даже наглядный, пульсации снизились примерно в 5-6 раз и это при том, что до переделки по выходу емкость была 940 мкФ, а теперь 660, так что и емкость уменьшили и пульсации снизили, надеюсь что и надежность заметно повысилась.
Если коротко, Panasonic очень понравились, все, Samwha тоже, но с ней я знаком давно и в принципе знал чего ожидать, но если хочется качественно, то лучше все таки Panasonic, в данном случае это была серия FR.
Как всегда буду рад комментариям и вопросам, надеюсь что обзор был полезен.
Как вычислить напряжение и вольтаж
Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.
Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.

Формулы измерения напряжения конденсаторов
Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.
Вам это будет интересно Как воздействует электрический ток на организм человека

В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.
Эквивалентная схема конденсатора
Эквивалентная схема: поскольку пластины в конденсаторе имеют некоторое сопротивление, и поскольку ни один диэлектрик не является идеальным изолятором, не существует такой вещи, как «идеальный» конденсатор. В реальной жизни конденсатор имеет как последовательное сопротивление, так и параллельное сопротивление (сопротивление утечки), взаимодействующие с его чисто емкостными характеристиками:

К счастью, относительно легко изготовить конденсаторы с очень маленьким последовательным сопротивлением и очень высоким сопротивлением утечки!
Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.
Среднее значение напряжения
Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.
То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.


Средневыпрямленное значение напряжения
Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.
На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения
Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.
Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды Ka:

Вот некоторые значения коэффициента амплитуды Ka для некоторых сигналов переменного напряжения:
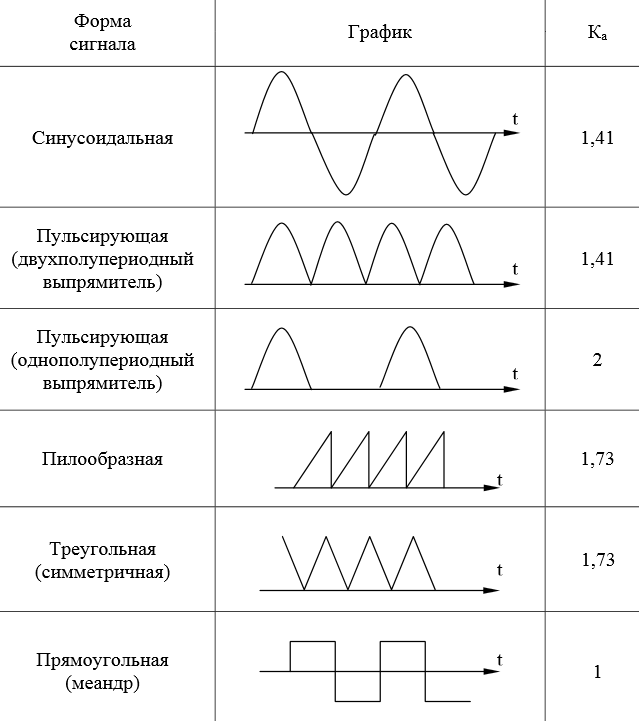
Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.
Как измерить среднеквадратичное значение напряжения
Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.
Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

Проведем небольшой опыт. Давайте соберем вот такую схемку:
Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц
А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?
Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:
.png)
Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды Ka= 1,73.
Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала



Проверяем нашим прибором, так ли оно на самом деле?
Супер! И в правду Тrue RMS.
Замеряем это же самое напряжение с помощью моего китайского мультиметра
Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.
Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».

Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.
Вот вам небольшая картинка, чтобы не путаться

- Сред. — средневыпрямленное значение сигнала. Это и есть площадь под кривой
- СКЗ — среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
- Пик. — амплитудное значение сигнала
- Пик-пик. — размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.
Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.
