Как найти среднее ожидаемое значение

Как найти среднее ожидаемое значение

Ожидаемое значение и среднее значение: в чем разница?

  • Редакция Кодкампа

17 авг. 2022 г.
читать 2 мин

Два термина, которые иногда взаимозаменяемо используются в статистике, — это ожидаемое значение и среднее значение .

Как правило, мы используем следующие термины в различных ситуациях:

  • Ожидаемое значение используется, когда мы хотим вычислить среднее значение распределения вероятностей. Это среднее значение, которое мы ожидаем получить до сбора каких-либо данных.
  • Среднее обычно используется, когда мы хотим вычислить среднее значение данной выборки. Это среднее значение необработанных данных, которые мы уже собрали.

Следующие примеры иллюстрируют, как вычислить ожидаемое значение и среднее значение на практике.

Пример: расчет ожидаемого значения

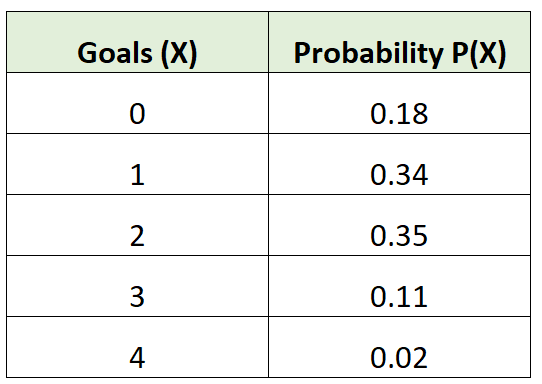
Распределение вероятностей говорит нам о вероятности того, что случайная величина примет определенные значения.

Например, следующее распределение вероятностей говорит нам о вероятности того, что определенная футбольная команда забьет определенное количество голов в данной игре:

Чтобы рассчитать ожидаемое значение этого распределения вероятностей, мы можем использовать следующую формулу:

Ожидаемое значение = Σx * P(x)

куда:

  • х : значение данных
  • P(x) : Вероятность значения

Например, мы рассчитали бы ожидаемое значение для этого распределения вероятностей следующим образом:

Ожидаемое значение = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 гола.

Это представляет собой ожидаемое количество голов, которое команда забьет в любой данной игре.

Пример: вычисление среднего

Обычно мы рассчитываем среднее значение после того, как фактически собрали необработанные данные.

Например, предположим, что мы записываем количество голов, забитых футбольной командой в 15 различных играх:

Забито голов: 1, 1, 0, 2, 2, 1, 0, 3, 1, 1, 1, 2, 4, 3, 1

Чтобы рассчитать среднее количество голов, забитых за игру, мы можем использовать следующую формулу:

Среднее значение = Σx i / n

куда:

  • x i : Необработанные значения данных
  • n : размер выборки

Например, мы могли бы рассчитать среднее количество забитых голов как:

Среднее значение = (1+1+0+2+2+1+0+3+1+1+1+2+4+3+1) / 15 = 1,533 гола.

Это среднее количество голов, забитых командой за игру.

Дополнительные ресурсы

В следующих руководствах содержится дополнительная информация о распределениях вероятностей:

Что такое таблица распределения вероятностей?
Как найти среднее значение распределения вероятностей
Как найти стандартное отклонение распределения вероятностей
Калькулятор распределения вероятностей

Источник

Ожидаемое значение случайной величины является важным количественным понятием в инвестициях. Инвесторы постоянно используют ожидаемые значения – при оценке выгод от альтернативных инвестиций, при прогнозировании прибыли на акцию и других корпоративных финансовых величин и коэффициентов, а также при оценке любых других факторов, которые могут повлиять на их финансовое положение.

Ожидаемое значение случайной величины определяется следующим образом:

Определение ожидаемого значения.

Ожидаемое значение случайной величины (или математическое ожидание, от англ. ‘expected value’) является средневзвешенной вероятностью возможных результатов случайной величины.

Для случайной величины (X) математическое ожидание (X) обозначается как (E(X)).

Ожидаемое значение (например, ожидаемая доходность акций) представляет собой либо будущее значение, например прогноз, либо «истинное» значение среднего (например, среднее значение для генеральной совокупности, которое обсуждается в чтении о статистических концепциях и доходности рынка). Следует различать ожидаемое значение и понятия исторического или выборочного среднего.

Выборочное среднее также суммирует в единственном числе центральное значение выборки. Тем не менее, выборочное среднее представляет собой центральное значение для определенного набора наблюдений в виде равно взвешенного среднего значения этих наблюдений.

Пример (8) анализа прибыли на акцию BankCorp.

Вы продолжаете свой анализ прибыли на акцию (EPS) BankCorp. В Таблице (3) вы представили распределение вероятностей для EPS BankCorp за текущий финансовый год.

Таблица 3. Распределение вероятностей для EPS BankCorp.

Вероятность

EPS ($)

0.15

2.60

0.45

2.45

0.24

2.20

0.16

2.00

1.00

Каково ожидаемое значение EPS BankCorp на текущий финансовый год?

Следуя определению математического ожидания, перечислите каждый результат, взвесьте его по вероятности и суммируйте взвешенные результаты.

( begin{aligned}
E(EPS) &= 0.15($2.60) + 0.45($2.45) + 0.24($2.20) + 0.16($2.00) \
&= $2.3405
end{aligned} )

Ожидаемое значение EPS составляет $2.34.

Формула, которое суммирует ваши вычисления в Примере (8):

( dst large begin{aligned}
E(X) &= P(X_l)X_l + P(X_2)X_2 + cdots + P (X_n)X_n \
&= dsum_{i=1}^{n}P(X_i)X_i
end{aligned}  ) (Формула 7)

где

(X_i) – один из (n) возможных результатов случайной величины (X).

Для простоты мы моделируем все случайные величины в этом чтении как дискретные случайные величины, которые имеют исчисляемый набор результатов. Для непрерывных случайных величин, которые обсуждаются вместе с дискретными случайными величинами в чтении об общих распределениях вероятностей, операция, соответствующая суммированию, является интегрированием.

Ожидаемое значение – это наш прогноз. Поскольку мы обсуждаем случайные величины, мы не можем рассчитывать на реализацию отдельного прогноза (хотя мы надеемся, что в среднем прогнозы будут точными).

В результате важно измерить риск, с которым мы сталкиваемся. Дисперсия и стандартное отклонение случайной величины измеряют разброс результатов вокруг ожидаемого значения или прогноза.

Определение дисперсии случайной величины.

Дисперсия случайной величины (англ. ‘variance of random variable’) – это ожидаемое значение (средневзвешенное по вероятности) квадратов отклонений от ожидаемого значения случайной величины:

( large dst
sigma^2(X) = E Big { big [ X – E(X) big ]^2 Big } ) (Формула 8)

Для дисперсии случайной величины используются два обозначения:  

( sigma^2(X) ) и ( mathrm{Var}(X) )

  • Дисперсия – это число, которое больше или равно 0, потому что это сумма квадратов.
  • Если дисперсия равна 0, дисперсия или риск отсутствуют.
  • Результат определенный, а величина (X) вовсе не случайна.
  • Дисперсия случайной величины больше 0 указывает на дисперсию (т.е. разброс) результатов.
  • Увеличение дисперсии случайной величины указывает на увеличение разброса результатов.

Дисперсия (X) – это величина, выраженная в квадратах единиц (X). Например, если случайная величина является процентной доходностью, дисперсия доходности выражается в процентах, возведенных в квадрат.

Стандартное отклонение случайной величины легче интерпретировать, чем дисперсию, поскольку оно выражено в тех же единицах, что и случайная величина. Если случайная величина выражена в процентах, то стандартное отклонение также будет выражено в процентах.

Обратите внимание, что в следующем примере там, где дисперсия доходности указывается в виде десятичной дроби, усложнения работы с «процентами в квадрате» не возникает.

Определение стандартного отклонения случайной величины.

Стандартное отклонение случайной величины (англ. ‘standard deviation of random variable’) – это положительный квадратный корень дисперсии случайной величины.

Лучший способ познакомиться с этими понятиями – это поработать с ними на примерах.

Пример (9) расчета дисперсии и стандартного отклонения для EPS BankCorp.

В Примере (8) вы рассчитали ожидаемое значение прибыли на акцию (EPS) BankCorp как $2.34, что является вашим прогнозом.

Теперь вы хотите измерить разброс вокруг вашего прогноза. В Таблице 4 показано ваше представление о вероятности распределения прибыли на акцию за текущий финансовый год.

Таблица 4. Распределение вероятностей для EPS BankCorp.

Вероятность

EPS ($)

0.15

2.60

0.45

2.45

0.24

2.20

0.16

2.00

1.00

Каковы дисперсия и стандартное отклонение EPS BankCorp для текущего финансового года?

Порядок расчета всегда предполагает сначала расчет ожидаемого значения, затем дисперсии, затем стандартное отклонение. Ожидаемое значение уже рассчитано.

Следуя приведенному выше определению дисперсии, рассчитайте отклонение каждого результата от среднего или ожидаемого значения, возведите в квадрат каждое отклонение, вычислите вес (умножьте) каждое квадратичное отклонение на вероятность его возникновения, а затем сложите эти результаты.

( small begin{aligned}
sigma^2(EPS) &= P($2.60)[$2.60 – E(EPS)]^2 + P($2.45)[$2.45 – E(EPS)]^2 \
&+ P($2.20)[$2.20 – E(EPS)]^2 + P($2.00)[$2.00 – E(EPS)]^2 \
&= 0.15(2.60 – 2.34)^2 + 0.45(2.45 – 2.34)^2 \
&+ 0.24(2.20 – 2.34)^2 + 0.16(2.00 – 2.34)^2 \
&= 0.01014 + 0.005445 + 0.004704 + 0.018496 = 0.038785
end{aligned} )

Стандартное отклонение – это положительный квадратный корень из 0.038785:

( sigma(EPS) = 0.038785^{1/2} = 0.196939 )

или приблизительно 0.20.

Формулой, с помощью которой выполняется ваш расчет дисперсии в Примере 9 будет:

(Формула 9)

(
begin{aligned}
sigma^2(X) &= P(X_l)big[ X_l – E(X) big]^2 + P(X_2)big[ X_2 – E(X) big]^2  \
&+ cdots + P(X_n)big[ X_n – E(X) big]^2 = \
&sum_{i=1}^{n}P(X_i) big[ X_i – E(X) big]^2
end{aligned} )

где

(X_i) – один из (n) возможных результатов случайной величины (X).

В инвестициях мы используем любую соответствующую информацию, доступную для составления наших прогнозов. Когда мы уточняем наши ожидания или прогнозы, мы обычно вносим корректировки на основе новой информации или событий; в этих случаях мы используем условные ожидаемые значения (англ. ‘conditional expected values’).

Ожидаемое значение случайной величины (X) для данного события или сценария ( S ) обозначается как ( E(X|S) ).

Предположим, что случайная величина (X) может принимать любое из (n) различных результатов ( X_1, X_2, …, X_n ) (эти результаты образуют набор взаимоисключающих и исчерпывающих событий).

Ожидаемое значение (X) при условии (S) – это первый результат, (X_i), умноженный на вероятность первого результата, заданного(S), ( P(X_1|S) ), плюс второй результат, (X_2), умноженный на вероятность второго результата, заданного (S), ( P(X_2|S) ) и так далее.

(Формула 10)

( large begin{aligned}
E(X|S) &= P(X_1|S)X_1 + P(X_2|S)X_2 \
&+ ldots + P(X_n|S)X_n
end{aligned} )

Мы проиллюстрируем эту формулу далее.

Параллельно с правилом полной вероятности для определения безусловных вероятностей существует принцип для определения (безусловных) ожидаемых значений.

Этот принцип является правилом полной вероятности для ожидаемого значения (англ. ‘total probability rule for expected value’).

Правило общей вероятности для ожидаемого значения.

( large E(X) = E(X|S)P(S) + E(X|S^C)P(S^C) ) (Формула 11)

(Формула 12)

( large begin{aligned}
E(X) &= E(X|S_1)P(S_1) + E(X|S_2)P(S_2) \
&+ ldots + E(X|S_n)P(S_n)
end{aligned} )

где

  • ( S_1, S_2, ldots, S_n ) – взаимоисключающие и исчерпывающие сценарии или события.

Формула 12, гласит, что ожидаемое значение (X) равно ожидаемому значению (X) для данного сценария 1, ( E(X|S_1) ), умноженному на вероятность сценария 1, ( P(S_1) ) плюс ожидаемое значение (X) для данного сценария 2, ( E(X|S_2) ), умноженное на вероятность сценария 2, ( P(S_2) ) и т.д.

Чтобы использовать этот принцип, мы формулируем взаимоисключающие и исчерпывающие сценарии, которые полезны для понимания результатов случайной величины. Этот подход был использован при разработке распределения вероятностей EPS в BankCorp в Примерах 8 и 9, которое мы сейчас обсудим.

Доходы BankCorp чувствительны к процентным ставкам, и корпорация получает выгоду в условиях снижения процентных ставок.

Предположим, есть вероятность 0.60, что BankCorp будет работать в условиях снижения процентных ставок в текущем финансовом году, и вероятность 0.40, что она будет работать в условиях стабильных процентных ставок (вероятность повышения процентных ставок оценивается как незначительная).

Если происходит снижение процентных ставок, вероятность того, что EPS составит $2.60, оценивается в 0.25, а вероятность того, что EPS составит $2.45, оценивается в 0.75.

Обратите внимание, что 0.60, вероятность снижения процентных ставок, умноженная на 0.25, вероятность EPS в $2.60 при условии снижения процентной ставки равна 0.15, (безусловная) вероятность $2.60 приведена в таблице в Примерах 8 и 9. Вероятности последовательны.

Кроме того, 0.60(0.75) = 0.45, вероятность прибыли на акцию в размере $2.45 приведена в Таблицах 3 и 4.

Древовидная диаграмма на Рисунке 2 показывает остальную часть анализа.

Рисунок 2. Анализ прогнозируемой прибыли на акцию (EPS) BankCorp. Рисунок 2. Анализ прогнозируемой прибыли на акцию (EPS) BankCorp.

Сценарий снижения процентных ставок указывает нам на узел дерева, который разветвляется до результатов в $2.60 и $2.45. Мы можем найти ожидаемую прибыль на акцию при условии снижения процентной ставки, используя Формулу 10, следующим образом:

E (EPS | Снижение процентных ставок) =
= 0.25($2.60) + 0.75($2.45) = $2.4875

Если процентные ставки стабильны,

E(EPS | Стабильные процентные ставки) =
= 0.60($2.20) + 0.40($2.00) = $2.12

Например, как только мы получаем новую информацию о том, что процентные ставки стабильны, мы пересматриваем наши первоначальные ожидания EPS с $2.34 вниз до $2.12.

Теперь, используя правило общей вероятности для ожидаемого значения, находим:

E(EPS) = E(EPS | Снижение процентных ставок) P(Снижение процентных ставок) + E(EPS | Стабильные процентные ставки) P(Стабильные процентные ставки)

Таким образом,

( E(EPS) = $2.4875(0.60) + $2.12(0.40) = $2.3405 )

или около $2.34.

Эта сумма идентична оценке ожидаемого значения EPS, рассчитанной непосредственно из распределения вероятностей в Примере 8. Так же, как и наши вероятности, ожидаемые значения должны быть согласующимися; в противном случае наши инвестиционные действия могут создать возможности получения прибыли для других инвесторов за наш счет.

Для анализа мы сначала разрабатываем факторы или сценарии, которые влияют на результат интересующего события. После присвоения вероятностей этим сценариям мы формируем ожидания, обусловленные различными сценариями.

Затем мы действуем в обратном направлении, чтобы получить ожидаемую стоимость на текущий момент. В рассмотренном выше примере EPS был интересующим нас событием, а изменение процентных ставок было фактором, влияющим на EPS.

Мы также можем рассчитать дисперсию EPS для каждого сценария:

(sigma^2)(EPS | Снижение процентных ставок)

= P(

$2.60 | Снижение процентных ставок)
(times)[$2.60 – E(EPS | Снижение процентных ставок)]2
+ P($2.45 | Снижение процентных ставок)
(times)[$2.45 – E(EPS | Снижение процентных ставок)]2

= 0.25(2.60 – $2.4875)2 + 0.75(2.45 – $2.4875)2 = 0.004219

(sigma^2)(EPS | Стабильные процентные ставки)

= P(

$2.20 | Стабильные процентные ставки)
(times) [$2.20 – E(EPS | Стабильные процентные ставки)]2
+ P($2.00 | Стабильные процентные ставки)
(times) [$2.00 – E(EPS | Стабильные процентные ставки)]2

= 0.60(2.20 – $2.12)2 + 0.40(2.00 – $2.12)2 = 0.0096

Это условные стандартные отклонения, т.е. дисперсия EPS при условии снижения процентных ставок и дисперсия EPS при условии стабильных процентных ставок. Связь между безусловной дисперсией и условной дисперсией является относительно сложной темой.

Безусловная дисперсия EPS представляет собой сумму двух слагаемых:

  1. ожидаемого значения (средневзвешенного по вероятности) условных дисперсий и
  2. дисперсии условных ожидаемых значений EPS.

Второе слагаемое возникает потому, что изменчивость условного ожидаемого значения является источником риска.

Первое слагаемое равно:

(sigma^2)(EPS) = P(Снижение процентных ставок) (sigma^2)(EPS | Снижение процентных ставок) + P(Стабильные процентные ставки) (sigma^2)(EPS | Стабильные процентные ставки)

= 0.60(0.004219) + 0.40(0.0096) = 0.006371

Второе слагаемое равно:

(sigma^2)[E(EPS | Среда процентных ставок)] =
0.60($2.4875 – $2.34)2 + 0.40($2.12 – $2.34)2 = 0.032414

Суммируя два слагаемых, находим безусловную дисперсию, которая равна:

0.006371 + 0.032414 = 0.038785

Основными моментами здесь является:

  1. то, что дисперсия, как и ожидаемое значение, имеет условный аналог безусловной концепции и
  2. то, что мы можем использовать условную дисперсию для оценки риска по конкретному сценарию.

Пример (10) анализа прибыли на акцию BankCorp.

Продолжая анализ показателей BankCorp, вы сосредоточитесь сейчас на структуре затрат BankCorp. Модель операционных расходов BankCorp, которую вы исследуете, это:

(  hat{Y} = a + bX  )

где

  • (  hat{Y} ) – прогноз операционных расходов в млн. долларов, а
  • X – количество филиалов корпорации

( hat{Y} ) представляет собой ожидаемое значение (Y) при условии (X) или (E (Y|X)).

(( hat{Y} )  – это обозначение, используемое в регрессионном анализе, который мы обсудим в следующих чтениях.)

Вы интерпретируете значение (a) как постоянные затраты, а (b) – как переменные затраты. Уравнение будет выглядеть следующим образом:

(  hat{Y} = 12.5 + 0.65X  )

BankCorp в настоящее время имеет 66 филиалов, и, согласно уравнению:

12.5 + 0.65(66) = $55.4 млн.

У вас есть два сценария роста, изображенные на древовидной диаграмме на Рисунке 3.

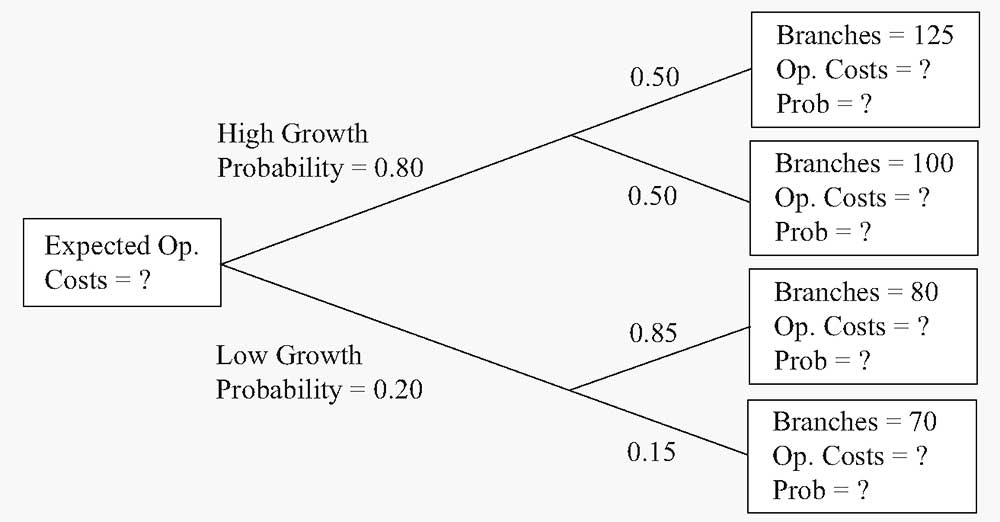
Рисунок 3. Прогнозируемые операционные расходы BankCorp. Рисунок 3. Прогнозируемые операционные расходы BankCorp.

  1. Рассчитайте прогнозируемые операционные расходы с учетом различных уровней операционных расходов, используя уравнение (  hat{Y} = 12.5 + 0.65X  ). Укажите вероятность каждого уровня из числа филиалов (см. вопросительные знак в крайних правых полях древовидной диаграммы).
  2. Рассчитайте ожидаемую стоимость операционных расходов в сценарии с высокими темпами роста. Также рассчитайте ожидаемую стоимость операционных расходов по сценарию низкого роста.
  3. Ответьте на вопрос в начальном поле дерева: каковы ожидаемые операционные расходы BankCorp?

Решение для части 1:

Используя уравнение ( hat{Y} = 12.5 + 0.65X  ) для ветвей дерева сверху вниз, находим:

Операционные расходы

Вероятность

( hat{Y}) = 12.5 + 0.65(125) = $93.75 млн.

0.80(0.50) = 0.40

( hat{Y}) = 12.5 + 0.65(100) = $77.50 млн.

0.80(0.50) = 0.40

( hat{Y}) = 12.5 + 0.65(80) = $64.50 млн.

0.20(0.85) = 0.17

( hat{Y}) = 12.5 + 0.65(70) = $58.00 млн.

0.20(0.15) = 0.03

Сумма = 1.00

 

Решение для части 2:

Суммы представлены в млн. долл.

E(операционные расходы | высокий рост) =
= 0.50(93.75) + 0.50(77.50) = $85.625

E(операционные расходы | низкий рост) =
= 0.85(64.50) + 0.15(58.00) = $63.525

 

Решение для части 3:

Суммы представлены в млн. долл.

E(операционные расходы) = E(операционные расходы | высокий рост) P(высокий рост)

+ E(операционные расходы | низкий рост) P(низкий рост)
= $85.625(0.80) + $63.525(0.20) = $81.205

Ожидаемые операционные расходы BankCorp составляют $81.205.

Мы снова увидим условные вероятности, когда будем обсуждать формулу Байеса. В этом разделе представлено несколько примеров проблем, которые можно решить с помощью вероятностных концепций.

Следующая проблема опирается на эти концепции, а также на аналитические навыки.

Пример (11) расчета премии за риск дефолта для долгового инструмента за один период.

Как соуправляющий портфеля краткосрочных облигаций, вы пересматриваете цену спекулятивной (дисконтной) облигации с нулевым купоном и сроком обращения 1 год. Для этого типа облигаций доход представляет собой разницу между уплаченной суммой и номинальной стоимостью, полученной при погашении.

Ваша цель – оценить соответствующую премию за риск дефолта для этой облигации. Вы определяете премию за риск дефолта как дополнительную доходность сверх безрисковой доходности, которая будет компенсировать инвесторам риск дефолта.

Если (R) – это обещанная доходность (доходность к погашению) по долговому инструменту, а (R_F) – безрисковая ставка, то премия за риск дефолта – это (R – R_F).

Вы оцениваете вероятность того, что риск дефолта облигации, обозначаемый как P(дефолт облигации) = 0,06.

Анализируя текущую доходность денежного рынка, вы обнаруживаете, что однолетние казначейские векселя США (T-bills) обеспечивают доходность в 2%, и вы используете эту ставку как (R_F).

В качестве первого шага вы делаете упрощенное предположение, что держатели облигаций ничего не возместят в случае дефолта.

Какая минимальная премия за риск вам требуется для этого инструмента?

Основная сложность в решении этого типа проблемы состоит в том, чтобы найти отправную точку. Во многих проблемах, включая эту, эффективным первым шагом является разделение возможных результатов на взаимоисключающие и исчерпывающие события экономически логичным способом.

Здесь, с точки зрения держателя облигации, есть два события, которые влияют на доходность, это:

  • дефолт облигации и
  • то, что дефолт облигации не произошел.

Эти два события охватывают все результаты.

Как эти события влияют на доход владельца облигации?

Вторым шагом является вычисление стоимости облигации для двух событий. У нас нет конкретных данных по номинальной стоимости облигации, но мы можем рассчитать стоимость за $1 или на одну вложенную денежную единицу.

Дефолт облигации

Дефолт облигации не произошел

Стоимость облигации

$0

$(1 + R)

Третий шаг – найти ожидаемую стоимость облигации (на 1 вложенный $).

E(Облигация) = $0 (times) P(Дефолт облигации) + $(1 + (R)) [1 – P(Дефолт облигации не произошел)]

Таким образом,

E(Облигация) = $(1 + (R)) [1 – P(Дефолт облигации)].

Ожидаемая стоимость безрискового казначейский вексель (Т-bill) на 1 вложенный $ составляет ( (1 + R_F) ).

Следующий шаг требует экономических суждений.

Вы хотите, чтобы премия за риск была достаточно большой, поэтому вы ожидаете, по крайней мере, безубыточности по сравнению с инвестированием в T-bill. Этот результат будет достигнут, если ожидаемая стоимость облигации будет равна ожидаемой стоимости Т-bill за 1 вложенный $.

Ожидаемая стоимость облигации = Ожидаемая стоимость T-Bill

$(1 + (R))[1 – P(Дефолт облигации) = (1 + (R_F))

Рассчитывая доход к погашению по облигации, вы найдете:

 (R) = {(1 +  (R_F))/[1 – P(Дефолт облигации)]} – 1

Подставляя в значения формулу, вы получите:

 (R) = [1.02/(1 – 0.06)] – 1 = 1.08511 – 1 = 0.08511

или около 8.51%, а премия за риск дефолта составит

 (R – R_F) = 8.51% – 2% = 6.51%.

Вам необходима премия за риск дефолта не менее 651 базисных пунктов. Вы можете заявить об этом следующим образом: если цена облигации составляет 8.51%, вы получите спред в 651 базисный пункт, а также получите номинальную сумму облигации с вероятностью 94%.

Однако, если произойдет дефолт, вы потеряете все. С премией в 651 базисный пункт, вы рассчитываете точку безубыточности относительно инвестиций в казначейские векселя. Поскольку инвестиции в облигации с нулевым купоном имеют переменную стоимость, если вы не склонны к риску, вы будете требовать, чтобы премия превышала 651 базисный пункт.

Этот анализ является отправной точкой. Владельцы облигаций обычно возмещают часть своих инвестиций в случае дефолта. Следующим шагом будет включение в анализ уровня возмещения средств в случае дефолта.

В этом разделе мы рассматривали случайные финансовые величины, такие как EPS, как отдельные значения. Мы не исследовали, как такие показатели, как ожидаемое значение и дисперсия EPS, могут быть функциями других случайных величин.

Доходность портфеля – это одна случайная величина, которая, очевидно, является функцией других случайных величин – случайных ставок доходности отдельных ценных бумаг в портфеле.

Чтобы проанализировать ожидаемую доходность портфеля и дисперсию доходности, мы должны понимать, что эти величины являются функцией характеристик доходности отдельных ценных бумаг. Глядя на дисперсию доходности портфеля, мы видим, что способ, которым меняется доходность каждой отдельной ценной бумаги меняется, чрезвычайно важен.

Чтобы понять значение этих изменений отдельных ценных бумаг портфеля, нам необходимо изучить некоторые новые концепции, – ковариацию и корреляцию. В следующем разделе, который касается ожидаемой доходности портфеля и дисперсии доходности, эти концепции будут рассмотрены.

Источник

Рассмотрим
основные характеристики дискретной
случайной величины при конечном числе
значений.

Каждому
значению дискретной случайной величины
отвечает его вероятность. Как отмечалось
выше, последовательность таких пар
образует ряд распределения дискретной
случайной величины:

где

,

,
i
=
1,…, n,

.

Если
случайная дискретная величина является
случайной альтернативной величиной,
т. е. задается двумя значениями 0 и 1 и
соответствующими им вероятностями
исходов q
=
1– р
и
р,
то
ряд распределения принимает форму:

,

где 0
≤
p ≤
1,
p +
q =
1.

На
основе ряда распределения можно
определить среднее значение случайной
дискретной величины как меру, которая
объединяет значения случайной дискретной
величины и их вероятности. Среднее
значение
есть
взвешенная средняя всех возможных
значений случайной величины, роль весов
(частот) играют вероятности.

Ожидаемое
среднее значение случайной величины
называется
математическим
ожиданием М(Х)
(оценкой,
которую ожидают получить).

Математическое
ожидание случайной дискретной величины
X
(т.
е. принимающей только конечное или
счетное множество значений x1,
x2,…,
хп
соответственно
с вероятностями р1,
p2,…,
рп)
равно сумме произведений значений
случайной величины на соответствующие
им вероятности:

.
(3.3)

Найдем
математическое ожидание случайной
величины X
– числа
рекламных объявлений в газете в заданный
день
для примера 3.1. Расчет
ожидаемого среднего значения случайной
величины удобно производить, пользуясь
табл. 3.3.

Таблица
3.3

Вычисление математического ожидания числа рекламных объявлений (пример 3.1)

хi

0

1

2

3

4

5

n

P(хi)

0,1

0,2

0,3

0,2

0,1

0,1

хiP(хi)

0,0

0,2

0,6

0,6

0,4

0,5

М(Х)
=
2,3

Можно
сказать, что в среднем 2,3 рекламных
объявления ежедневно помещаются в
газете. Это – ожидаемое
среднее
число рекламных объявлений в заданный
день.

3.5. Свойства математического ожидания случайной дискретной величины

Математическое
ожидание случайной дискретной величины
обладает следующими свойствами:

1. M(C)
= С,

где С
– постоянная величина.

2.
М(С·Х)
=
С·М(Х),

где С
–
постоянная величина.

3. М(Х1
±
Х2
±…± Хn)
= М(Х1)
± М(Х2)
±…± М(Хn).
(3.4)

4. Для
конечного числа п
независимых
случайных величин:

М(Х1∙
Х2∙…∙Хn)
=
М(Х1)
∙М(Х2)
∙…∙М(Хn).


(3.5)

5.
М(Х–C)
=
М(Х)
–
C.

Следствие.
Математическое
ожидание отклонения значений случайной
величины X
от
ее математического ожидания равно нулю:

М[Х
–
М(Х)]
=
0. (3.6)

6.
Математическое ожидание среднего
арифметического значения п
одинаково
распределенных взаимно независимых
случайных
величин равно математическому ожиданию
каждой из величин:

.
(3.11)

Случайные
дискретные величины называются одинаково
распределенными, если у них одинаковые
ряды распределения, а следовательно, и
одинаковые числовые характеристики.

Пусть
Х1,
Х2,…,
Хn
– одинаково
распределенные случайные величины,
математические ожидания каждой из
которых одинаковы и равны а.
Тогда
математическое ожидание их суммы равно
nа
и
математическое ожидание средней
арифметической равно а:

.

Пример
3.4.
Для
лотереи, описанной в примере
3.2, составим
закон распределения суммы выигрыша
посетителя магазина, который приобрел
два билета стоимостью по 1 руб. Найдем
математическое ожидание суммы выигрыша
и убедимся в справедливости формулы
М(Х
+
Y)
= М(Х)
+ М(Y).

Решение.
Суммы
выигрышей на первый и второй билеты
лотереи с учетом затрат на их приобретение
являются случайными величинами, которые
обозначим соответственно X
и
Y.
Это
одинаково распределенные случайные
величины, а их законы распределения
получены в примере 3.2. Сумма выигрыша
для посетителя, который приобрел два
билета, является случайной величиной.
Она представляет собой сумму случайных
величин Х
и
Y, которые
являются зависимыми.
Для
нахождения закона распределения
случайной величины X+Y
рассмотрим
возможные различные исходы лотереи
(табл. 3.4).

Таблица
3.4

Источник


Загрузить PDF


Загрузить PDF

Ожидаемое значение – это понятие, используемое в статистике. При этом находится среднее взвешенное значение путем суммирования произведений каждого возможного результата на его вероятность. Ожидаемое значение – некая средняя величина, конкретное значение которой может не соответствовать ни одному из возможных событий: например, при бросании 6-гранной игральной кости ожидаемое значение равно 3,5. Для вычисления этого значения необходимо знать все возможные результаты и вероятность каждого из них.

Шаги

  1. Изображение с названием Calculate an Expected Value Step 1

    1

    Внимательно ознакомьтесь с ситуацией. Прежде чем пронумеровать возможные события и присвоить им соответствующие вероятности, убедитесь, что учли все возможные результаты. Рассмотрим, например, игру в кости со ставкой $10. Подбрасывается 6-гранный кубик, и ваш выигрыш зависит от того, какая цифра выпала: 6 приносит выигрыш $20 (или $30 с учетом вашей ставки), 5 дает вам $10 ($20 с учетом вашей ставки), при выпадении же любой другой цифры вы ничего не выигрываете, то есть теряете свою ставку в $10.

  2. Изображение с названием Calculate an Expected Value Step 2

    2

    Пронумеруйте все возможные исходы. В данном случае полезно выписать их в таблицу. В нашем примере всего 6 возможных событий: (1) выпадает 1, вы теряете $10, (2) 2 – потеря $10, (3) 3 – потеря $10, (4) 4 – потеря $10, (5) выпадает 5, и вы выигрываете $10, (6) выпадает 6, принося вам $20. Обратите внимание, что величина ставки $10 вычтена из каждого результата, то есть приведен чистый выигрыш.

  3. Изображение с названием Calculate an Expected Value Step 3

    3

    Определите вероятность каждого события. В нашем примере все 6 исходов равновероятны. При бросании игрового кубика вероятность выпадения определенного номера равна 1 поделенному на 6, или 16,7 процентов. Вероятности событий также полезно внести в таблицу, особенно в случае, если они не настолько просто определяются, как в нашем примере.

  4. Изображение с названием Calculate an Expected Value Step 4

    4

    Вычислите ожидаемое значение. При этом используйте выписанные вами возможные исходы и их вероятности. Воспользуйтесь следующей формулой: O1*P1 + O2*P2 + O3*P3 и так далее. Множитель “O” обозначает отдельное событие, а “P” – вероятность соответствующего события.

    • В нашем примере ожидаемое значение игры в кости равно (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (10 * 0,167) + (20 * 0,167), или – $1,67. Таким образом, садясь играть в кости, приготовьтесь терять $1,67 в каждом раунде.

      Изображение с названием Calculate an Expected Value Step 4Bullet1

  5. Изображение с названием Calculate an Expected Value Step 5

    5

    Подумайте о смысле ожидаемого значения. В нашем примере вероятность выигрыша была определена как – $1,67 за раунд. Такое событие, естественно, не возможно при однократном броске кости: в одном раунде вы можете потерять $10, либо выиграть $10 или $20. Тем не менее, ожидаемое значение полезно при оценке долгосрочных результатов. Если вы играете вновь и вновь, вы будете терять в среднем $1,67 за один бросок кубика. Значит, такая игра не выгодна для вас.

    • Чем больше испытаний проводится, тем ближе их результат к ожидаемому значению. Например, вы сыграли 5 раз подряд и проиграли $10. Однако, если бы вы сыграли 100 раз подряд или больше, сумма вашего выигрыша или проигрыша вплотную приблизилась бы к ожидаемому значению. Это так называемый “закон больших чисел”.
    • Выше приведенный простой пример служит иллюстрацией того, как устроены азартные игры. Ваш усредненный выигрыш отрицателен, что означает выгоду для игрового дома. Тем не менее, азарт и надежда на крупный выигрыш привлекают все новых игроков.

    Реклама

Советы

  • При наличии большого количества возможных событий вы можете создать электронную таблицу, занося в нее события и их вероятности.
  • В приведенном выше примере можно использовать и другие денежные единицы, цифры от этого не изменятся.

Реклама

Что вам понадобится

  • Карандаш
  • Лист бумаги
  • Калькулятор

Об этой статье

Эту страницу просматривали 10 671 раз.

Была ли эта статья полезной?

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 октября 2021 года; проверки требуют 7 правок.

Математи́ческое ожида́ние — понятие в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины[1]. В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения (более строгие определения см. ниже). Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.

Обозначается через {mathbb {E}}[X][2] (например, от англ. Expected value или нем. Erwartungswert);
в русскоязычной литературе также встречается обозначение M[X] (возможно, от англ. Mean value или нем. Mittelwert, а возможно от «Математическое ожидание»). В статистике часто используют обозначение mu .

Для случайной величины, принимающей значения только 0 или 1 математическое ожидание равно p — вероятности «единицы». Математическое ожидание суммы таких случайных величин равно np, где n — количество таких случайных величин. При этом вероятности появления определенного кол-ва единиц рассчитываются по биномиальному распределению. Поэтому в литературе, скорее всего, легче найти запись, что мат. ожидание биномиального распределения равно np[3].

Некоторые случайные величины не имеют математического ожидания, например, случайные величины, имеющие распределение Коши.

На практике математическое ожидание обычно оценивается как среднее арифметическое наблюдаемых значений случайной величины (выборочное среднее, среднее по выборке). Доказано, что при соблюдении определенных слабых условий (в частности, если выборка является случайной, то есть наблюдения являются независимыми) выборочное среднее стремится к истинному значению математического ожидания случайной величины при стремлении объема выборки (количества наблюдений, испытаний, измерений) к бесконечности.

Определение[править | править код]

Общее определение через интеграл Лебега[править | править код]

Пусть задано вероятностное пространство (Omega,mathfrak{A},mathbb{P}) и определённая на нём случайная величина X. То есть, по определению, Xcolon Omega to mathbb {R}  — измеримая функция. Если существует интеграл Лебега от X по пространству Omega , то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается M[X] или {mathbb {E}}[X].

{displaystyle mathbb {E} [X]=int limits _{Omega }!X(omega ),mathbb {P} (domega ).}

Определение через функцию распределения случайной величины[править | править код]

Если F_{X}(x) — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:

{displaystyle mathbb {E} [X]=int limits _{-infty }^{infty }!x,dF_{X}(x)}, {displaystyle xin mathbb {R} }.

Определение для абсолютно непрерывной случайной величины (через плотность распределения)[править | править код]

Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью f_{X}(x), равно

{displaystyle mathbb {E} [X]=int limits _{-infty }^{infty }!xf_{X}(x),dx}.

Определение для дискретной случайной величины[править | править код]

Если X — дискретная случайная величина, имеющая распределение

{displaystyle mathbb {P} (X=x_{i})=p_{i}} , {displaystyle sum limits _{i=1}^{infty }p_{i}=1},

то прямо из определения интеграла Лебега следует, что

{displaystyle mathbb {E} [X]=sum limits _{i=1}^{infty }x_{i},p_{i}}.

Математическое ожидание целочисленной величины[править | править код]

  • Если X — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
{displaystyle mathbb {P} (X=j)=p_{j}} , {displaystyle j=0,1,dotsc }, {displaystyle sum limits _{j=0}^{infty }p_{j}=1},

то её математическое ожидание может быть выражено через производящую функцию последовательности {p_{i}}

P(s)=sum _{{k=0}}^{infty };p_{k}s^{k}

как значение первой производной в единице: {displaystyle mathbb {E} [X]=P'(1)}. Если математическое ожидание X бесконечно, то lim _{{sto 1}}P'(s)=infty и мы будем писать {displaystyle P'(1)=mathbb {E} [X]=infty }

Теперь возьмём производящую функцию Q(s) последовательности «хвостов» распределения {q_{k}}

{displaystyle q_{k}=mathbb {P} (X>k)=sum _{j=k+1}^{infty }{p_{j}}} , {displaystyle Q(s)=sum _{k=0}^{infty }q_{k}s^{k}.}

Эта производящая функция связана с определённой ранее функцией P(s) свойством: Q(s)={frac {1-P(s)}{1-s}} при |s|<1. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:

{displaystyle mathbb {E} [X]=P'(1)=Q(1)}

Математическое ожидание случайного вектора[править | править код]

Пусть X=(X_{1},dots ,X_{n})^{{top }}colon Omega to {mathbb {R}}^{n} — случайный вектор. Тогда по определению

{displaystyle mathbb {E} [X]=(mathbb {E} [X_{1}],dots ,mathbb {E} [X_{n}])^{top }},

то есть математическое ожидание вектора определяется покомпонентно.

Математическое ожидание преобразования случайной величины[править | править код]

Пусть gcolon {mathbb {R}}to {mathbb {R}} — борелевская функция, такая что случайная величина Y = g(X) имеет конечное математическое ожидание. Тогда для него справедлива формула

{displaystyle mathbb {E} left[g(X)right]=sum limits _{i=1}^{infty }g(x_{i})p_{i},}

если X имеет дискретное распределение;

{displaystyle mathbb {E} left[g(X)right]=int limits _{-infty }^{infty }!g(x)f_{X}(x),dx,}

если X имеет абсолютно непрерывное распределение.

Если распределение mathbb {P} ^{X} случайной величины X общего вида, то

{displaystyle mathbb {E} left[g(X)right]=int limits _{-infty }^{infty }!g(x),mathbb {P} ^{X}(dx).}

В специальном случае, когда {displaystyle g(X)=X^{k}}, математическое ожидание {displaystyle mathbb {E} [g(X)]=mathbb {E} [X^{k}]} называется k-м моментом случайной величины.

Свойства математического ожидания[править | править код]

  • Математическое ожидание числа (не случайной, фиксированной величины, константы) есть само число.
{displaystyle mathbb {E} [a]=a}
ain {mathbb {R}} — константа;
  • Математическое ожидание линейно[4], то есть
{displaystyle mathbb {E} [aX+bY]=amathbb {E} [X]+bmathbb {E} [Y]},
где X,Y — случайные величины с конечным математическим ожиданием, а a,bin mathbb{R} — произвольные константы;

В частности, математическое ожидание суммы (разности) случайных величин равно сумме (соответственно — разности) их математических ожиданий.

{displaystyle 0leqslant mathbb {E} [X]leqslant mathbb {E} [Y]}.
  • Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если X=Y почти наверняка, то
{displaystyle mathbb {E} [X]=mathbb {E} [Y]}.
  • Математическое ожидание произведения двух независимых или некоррелированных[5] случайных величин X,Y равно произведению их математических ожиданий
{displaystyle mathbb {E} [XY]=mathbb {E} [X]cdot mathbb {E} [Y]}.

Неравенства, связанные с математическим ожиданием[править | править код]

Неравенство Маркова — для неотрицательной случайной величины {displaystyle Xcolon Omega to mathbb {R} ^{+}} определённой на вероятностном пространстве (Omega ,{mathcal {F}},{mathbb {P}}) с конечным математическим ожиданием {displaystyle mathbb {E} (X)} выполняется неравенство:

{displaystyle mathbb {P} left(Xgeqslant aright)leqslant {frac {mathbb {E} (X)}{a}}}, где a>0.

Неравенство Йенсена для математического ожидания выпуклой функции от случайной величины. Пусть (Omega ,{mathcal {F}},mathbb {P} ) — вероятностное пространство, {displaystyle Xcolon Omega to mathbb {R} } — определённая на нём случайная величина, varphi colon {mathbb {R}}to {mathbb {R}} — выпуклая борелевская функция, такие, что X,varphi (X)in L^{1}(Omega ,{mathcal {F}},{mathbb {P}}), то

{displaystyle varphi (mathbb {E} (X))leqslant mathbb {E} (varphi (X))}.

Теоремы, связанные с математическим ожиданием[править | править код]

{displaystyle lim limits _{nto infty }mathbb {E} (X_{n})=mathbb {E} (X)} .
{displaystyle mathbb {E} left(sum _{i=1}^{N}X_{i}right)=mathbb {E} (N)mathbb {E} (X)}
{displaystyle mathbb {E} (X)=G'(0)}.

Примеры[править | править код]

  • Пусть случайная величина имеет дискретное равномерное распределение, то есть mathbb {P} (X=x_{i})={frac {1}{n}},;i=1,ldots ,n. Тогда её математическое ожидание
{displaystyle mathbb {E} [X]={frac {1}{n}}sum limits _{i=1}^{n}x_{i}}

равно среднему арифметическому всех принимаемых значений.

{displaystyle mathbb {E} [X]=int limits _{a}^{b}!{frac {x}{b-a}},dx={frac {a+b}{2}}}.
  • Пусть случайная величина X имеет стандартное распределение Коши. Тогда
int limits _{-infty }^{infty }!xf_{X}(x),dx=infty ,

то есть математическое ожидание X не определено.

См. также[править | править код]

  • Дисперсия случайной величины
  • Моменты случайной величины
  • Условное математическое ожидание

Примечания[править | править код]

  1. ↑ «Математическая энциклопедия» / Главный редактор И. М. Виноградов. — : «Советская энциклопедия», 1979. — 1104 с. — (51[03] М34). — 148 800 экз.
  2. ↑ А. Н. Ширяев. 1 // «Вероятность». — : МЦНМО, 2007. — 968 с. — ISBN 978-5-94057-036-3, 978-5-94057-106-3, 978-5-94057-105-6.
  3. ↑ В.Е.Гмурман. Часть вторая. Случайные величины. ->
    Глава 4. Дискретные случайные величины. ->
    Параграф 3.     // [http://elenagavrile.narod.ru/ms/gmurman.pdf РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ И
    МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ]. — 1979. — С. 63. — 400 с.     Архивная копия от 21 января 2022 на Wayback Machine
  4. ↑ Пытьев Ю. П., Шишмарев И. А., Теория вероятностей, математическая статистика и элементы теории возможностей для физиков. — М.: Физический факультет МГУ, 2010.
  5. ↑ Теория вероятностей: 10.2. Теоремы о числовых характеристиках. sernam.ru. Дата обращения: 10 января 2018. Архивировано 10 января 2018 года.

Литература[править | править код]

  • Феллер В. Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons, Volume I second edition / Перевод с англ. Р. Л. Добрушина, А. А. Юшкевича, С. А. Молчанова Под ред. Е. Б. Дынкина с предисловием А. Н. Колмогорова. — 2-е изд. — М.: Мир, 1964. — С. 270—272.

Ссылки[править | править код]

  • Математическое ожидание и его свойства на http://www.toehelp.ru
Источник

Добавить комментарий