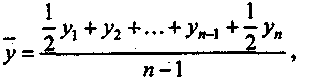Как найти среднее по годам - Сайт, где вы сможете решить свои вопросы

Среднегодовой темп роста применяется при анализе рядов динамики для выявления общей тенденции изменения показателя во времени.

Как видно из названия – это усредненный показатель. Его значение говорит о том, что если бы каждый год темп роста был одинаковым и равен среднему, то общий рост показателя был равен фактическому.

Среднегодовой темп роста можно определить двумя способами:

Tp‾=yny1n−1∗100%overline{T_p}=sqrt[n-1]{frac{y_n}{y_1}}*100%,

где yny_n — значение показателя отчетного периода;

y1y_1 — значение показателя базового периода;

nn — количество лет.

Tp‾=Kp2∗Kp3∗…∗Kpnn−1∗100%overline{T_p}=sqrt[n-1]{K_p^2*K_p^3*…*K_p^n}*100%,

где KpiK_p^i — цепной коэффициент роста за i-й период.

Примеры решения задач

Пример 1

В 2010 году на предприятии было выпущено продукции на 3650 тыс. руб., а в 2017 — на 4251 тыс. руб. Найти среднегодовой темп роста выпуска продукции.

Решение

Tp‾=425136508−1∗100%=102,2%overline{T_p}=sqrt[8-1]{frac{4251}{3650}}*100%=102,2%

В среднем за год выпуск продукции возрастал на 2,2%.

Ответ: Tp‾=102,2%overline{T_p}=102,2%

Пример 2

Рассчитать среднегодовой темп роста с использованием коэффициентов роста.

Год	2010	2011	2012	2013	2014	2015	2016	2017
Объем выпуска, тыс. шт.	1020	1021	1300	1250	1280	1310	1390	1460

Решение

Решим данную задачу средствами MS Excel.

Коэффициент роста определяется как отношение показателя текущего года к предыдущему.

Получаем

Далее необходимо получить произведение этих коэффициентов.

Извлекаем корень 7-й степени. Это возможно двумя путями

Или

Также среднегодового темпа роста при помощи средней геометрической

Получили

Ответ: 105,26%.

Не можешь разобраться в этой теме?

Обратись за помощью к экспертам

Гарантированные бесплатные доработки

Быстрое выполнение от 2 часов

Проверка работы на плагиат

Источник

17 авг. 2022 г.
читать 2 мин

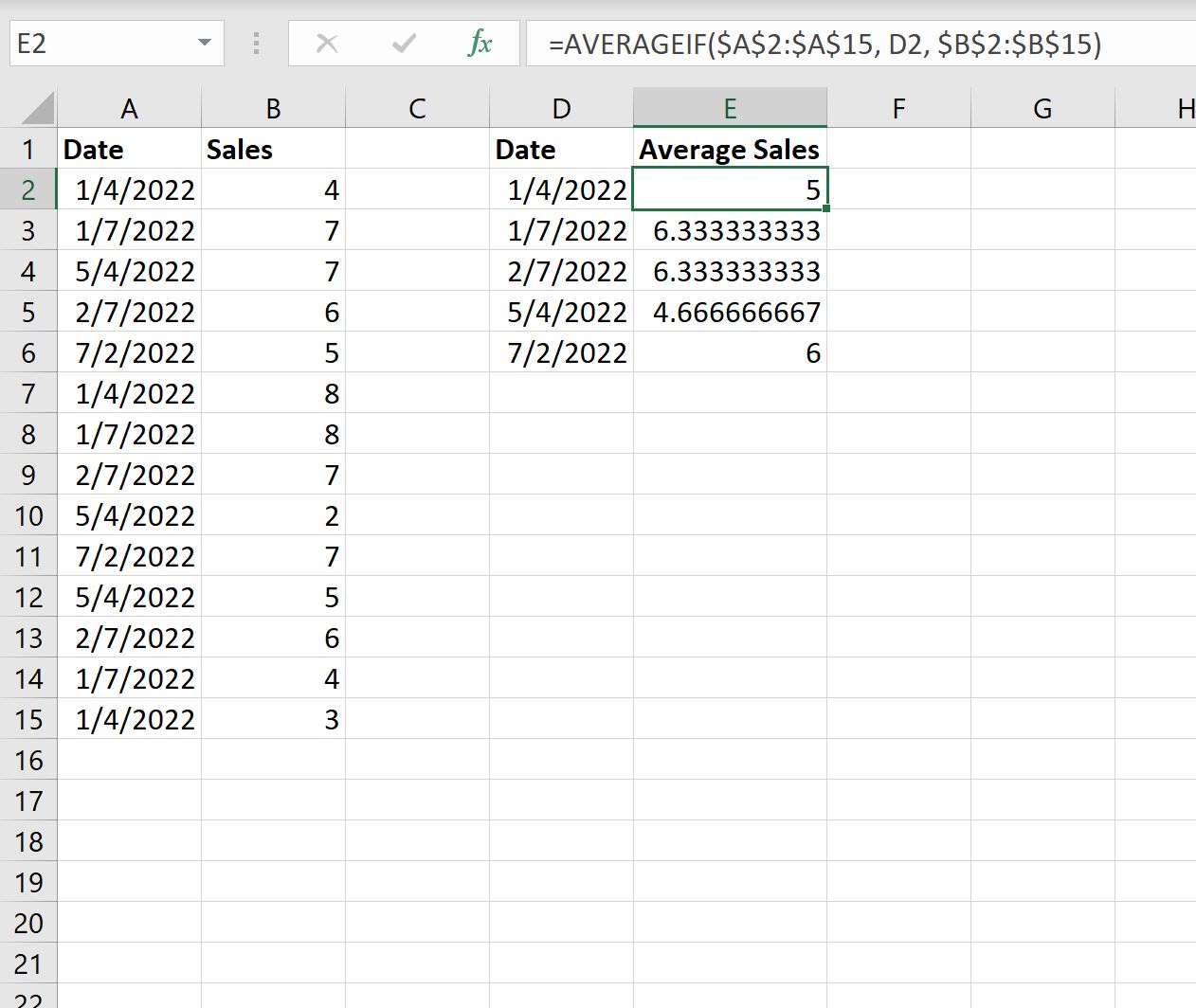
Вы можете использовать следующую формулу для расчета среднего значения по дате в электронной таблице Excel:

=AVERAGEIF( A1:A10 , C1 , B1:B10 )

Эта конкретная формула вычисляет среднее значение в диапазоне ячеек B1:B10 , только если соответствующие ячейки в диапазоне A1:A10 равны дате в ячейке C1 .

В следующем примере показано, как использовать эту формулу на практике.

Пример: вычислить среднее значение по дате в Excel

Предположим, у нас есть следующий набор данных, который показывает продажи некоторого продукта в разные даты:

Теперь предположим, что мы хотим рассчитать средний объем продаж по дате.

Чтобы создать список уникальных дат, мы можем использовать следующую формулу:

=SORT(UNIQUE( A2:A15 ))

Мы введем эту формулу в ячейку D2 :

По умолчанию Excel преобразует дату в количество дней с 01.01.1900.

Чтобы преобразовать эти числа в распознаваемый формат даты, просто выделите диапазон ячеек D2:D6 , затем щелкните стрелку раскрывающегося списка формата и выберите «Короткая дата» :

Даты будут преобразованы в распознаваемый формат даты:

Затем мы можем использовать следующую формулу для расчета средних продаж по дате:

=AVERAGEIF( $A$2:$A$15 , D2 , $B$2:$B$15 )

Мы введем эту формулу в ячейку E2 , затем скопируем и вставим ее в каждую оставшуюся ячейку в столбце E:

Из вывода мы видим:

Средний объем продаж на 04.01.2022 составляет 5 .
Средний объем продаж на 07.01.2022 – 6333 .
Средний объем продаж на 07.02.2022 — 6333 .

И так далее.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:

Как считать по месяцам в Excel
Как считать по годам в Excel
Как подсчитать, если ячейки содержат текст в Excel

Написано

Замечательно! Вы успешно подписались.

Добро пожаловать обратно! Вы успешно вошли

Вы успешно подписались на кодкамп.

Срок действия вашей ссылки истек.

Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.

Успех! Ваша платежная информация обновлена.

Ваша платежная информация не была обновлена.

Источник

Наряду с абсолютными
и относительными величинами в статистике
большое применение находят средние
величины. В
повседневной жизни употребляются
термины “в среднем”, “средняя”.
Например, средняя цена, средний расход
продуктов, средняя заработная плата,
средняя мощность оборудования, средняя
выработка, средний размер сбережений
и т. д.

В экономическом
анализе часто приходится оперировать
средними величинами в целях лучшего
понимания общей картины, когда нужно
из многих признаков получить величину,
в которой отражались бы свойства всех
признаков, входящих в состав совокупности.

Средняя величина
в С – обобщающий показатель,
характеризующий типичный уровень
явления в конкретных условиях места
и времени, отражающий величину
варьирующего признака в расчете на
единицу качественно однородной
совокупности.

Средняя величина есть обобщающая
количественная характеристика однородных
явлений по какому-либо варьирующему
признаку.

Применение средних
величин позволяет охарактеризовать
определенный признак совокупности
одним числом, несмотря на количественные
различия единиц по данному признаку
внутри совокупности.

Следовательно,
средняя величина есть обобщающая
характеристика совокупности; средняя
величина выражает типичное свойство
совокупности; средняя величина —
величина абстрактная, а не конкретная,
так как в ней сглаживаются отдельные
значения единиц совокупности, имеющие
отклонения в ту и другую сторону;
реальность средней величины достигается,
если она вычисляется из одной совокупности.

Пользуясь средними
величинами при анализе массовых явлений,
необходимо всегда помнить, что часто в
средней величине скрываются отстающие
хозяйствующие субъекты, которые имеют
низкие показатели своей деятельности
и, наоборот, не выявляются фирмы, компании,
предприятия и т. д., которые работают
весьма эффективно. Это возможно, как
уже говорилось выше, в связи со свойством
средней, в которой отклонения отдельных
значений признака от ее величины взаимно
погашаются. (Так, например, при условии
выполнения плана розничного товарооборота
в целом по холдингу, занимающемуся
продажей товаров, часть фирм, входящих
в него, не выполнила план и, наоборот,
другая часть перевыполнила план
товарооборота.) Поэтому, кроме средней,
следует использовать и отдельные
индивидуальные показатели работы фирм,
входящих в холдинг.

В эк. практике
исп.-ся широкий круг показателей,
вычисленных в виде средних величин.

Напр, обобщающим
показателем доходов рабочих АО служит
средний доход одного рабочего, определяемый
отношением фонда з/п и выплат социального
характера за рассматриваемый период
(год, квартал, месяц) к численности
рабочих АО.

Вычисление
среднего – один
из распространенных приемов обобщения;
средний показатель отражает то общее,
что характерно (типично) для всех единиц
изучаемой совокупности, в то же время
он игнорирует различия отдельных
единиц. В каждом явлении и его развитии
имеет место сочетание случайности
и необходимости.
При исчислении средних в силу действия
закона больших чисел случайности
взаимопогашаются, уравновешиваются,
поэтому можно абстрагироваться от
несущественных особенностей явления,
от колич. значений признака в каждом
конкретном случае. В способности
абстрагироваться от случайности
отдельных значений, колебаний и
заключена научная
ценность средних как обобщающих
характеристик совокупностей.

Там, где возникает
потребность обобщения, расчет таких
характеристик приводит к замене множества
различных инд. значений признака средним
показателем, характеризующим всю
совокупность явлений, что позволяет
выявить закономерности, присущие
массовым общ. явлениям, незаметные в
единичных явлениях.

Средняя отражает
характерный, типичный, реальный уровень
изучаемых явлений, характеризует эти
уровни и их изменения во времени и в
пространстве; это сводная характеристика
закономерностей процесса в тех условиях,
в к-рых он протекает.

Выбор
вида средней
определяется эк. содержанием
определенного показателя и исходных
данных.

1)- Класс
степенных средних
– арифметическая,
гармоническая, геометрическая,
квадратическая, кубическая
и т.д. Помимо
степенных средних в с/практике используются

2) Структурные
средние –
применяются для изучения внутреннего
строения и структуры рядов распределения
значений признака. К таким показателям
относятся мода
и медиана..

Средняя хронологическая

Средняя
хронологическая — это средний уровень
ряда динамики, т. е.
средняя,
исчисленная по совокупности значений
показателя в разные моменты или периоды
времени. В
зависимости от вида ряда динамики
применяются различные способы ее
расчета, а именно расчет средней
хронологической интервального ряда и
средней хронологической моментного
ряда.

Средней
хронологической интервального ряда
является средняя величина из уровней
интервального ряда динамики,
которая исчисляется по формуле

где
— средний уровень ряда;

у
— уровень ряда динамики;

n
— число членов ряда.

Средней
хронологической моментного ряда является
средняя величина из уровней моментного
ряда динамики.
Если f(t)
есть функция, выражающая изменение
моментного показателя во времени, то
за время (t)
от а
до b
средняя хронологическая моментyого
ряда равна:

Однако данных
непрерывного наблюдения значения f(t)
в распоряжении статистики, как правило,
нет. Поэтому в зависимости от характера
изменения показателя и имеющихся данных
применяются различные методы расчета.
При равных промежутках времени между
датами, на которые имеются данные, и
равномерном изменении размера показателя
между датами средняя хронологическая
моментного ряда обычно исчисляется
по формуле:

где у
— уровень ряда; n
— число всех
членов ряда;
—
средний уровень.

Если периоды
времени, отделяющие одну дату от другой,
не равны между собой, то расчет средней
хронологической моментного ряда
производится по формуле средней
взвешенной арифметической, в качестве
весов которой принимаются отрезки
времени между датами, т. е. по формуле:

гдеТ—
время, в течение которого данный уровень
ряда (у)
оставался без изменения.

Известно, например,
что в январе 2007 года произошло следующее
изменение численности сотрудников
компании “Бест”: было на 1 января
551 чел., уволился 2 января один сотрудник,
было принято 6 января 24 человека, 16
января— 6 человек, уволилось 25 января—
10 сотрудников. Требуется определить
среднюю численность сотрудников компании
“Бест” в январе 2007 г. Рассчитаем
число календарных дней, в течение которых
численность сотрудников компании “Бест”
оставалась без изменения, и произведение
этих чисел.

Таблица 5

Данные для расчета средней численности сотрудников компании “Бест”

Численность сотрудников компании «Бест», чел.(y)	Число календарных дней, в течение которых данная численность сотрудников оставалась безизменения (T)	Произведение численности сотрудников на число календарных дней(yT)
551	1	551
550	4	2200
574	10	5740
580	9	5220
570	7	3990
ИТОГО	31	17701

Используя данные
произведенных расчетов, получим:

В отличие от первого
способа расчета средней хронологической
моментного ряда второй способ дает
точное значение средней.

Средняя гармоническая (сг).

СГ применяется
в тех случаях, когда частоты (веса) не
приводятся непосредственно, а входят
сомножителями в один из имеющихся
показателей.

Пример. Автомобиль
доставил товары в три магазина фирмы
“Весна”, которые удалены от головного
предприятия на одинаковое расстояние.
Так, до первого магазина, расположенного
на шоссейной дороге, автомобиль прошел
путь со скоростью 50 км/ч, до второго, по
проселочной дороге, — 40 км/ч, а в третьем
случае автомобилю пришлось полпути
пройти через лесной массив, и скорость
движения составила только 30 км/ч.

Требуется определить
среднюю скорость движения автомобиля.
На первый взгляд представляется, что
средняя скорость • движения может быть
определена по формуле простой
арифметической:

Однако нетрудно
убедиться, что средняя вычислена
неправильно. В самом деле, производя
расчет средней скорости по простой
арифметической средней, исходим из
того, что автомобиль во всех трех случаях
прошел одинаковое расстояние, пройдя
соответственно 50, 40 и 30 км, т. е. всего
120 км. Если бы условие этой задачи
было сформулировано в такой форме, то
средняя была бы рассчитана правильно
и характеризовала бы пройденное
автомобилем среднее расстояние.

В действительности
же эта средняя рассчитана неверно, так
как «в условия задачи не следует, что
автомобиль на преодоление расстояния
до трех магазинов фирмы “Весна”
проехал 120 км, так как Скорость движения
была различная. Следовательно, он прошел
и разное расстояние.

В тех случаях,
когда вес каждого варианта равен единице
(индивидуальные значения обратного
признака встречаются по одному разу),
применяется СГ
простая,
исчисляемая по формуле:

где x
– отдельные варианты обратного
признака, встречающиеся по одному разу;
n–
число вариантов.

(8)

или
в сокращенном виде

где

—средняя
гармоническая;
—
числа, обратные заданным вариантам.

Иначе говоря, СГ
простая
отношение числа вариантов к сумме
обратных значений этих вариантов.

Для нашего примера
будем иметь:

В нашем примере
СА (х_а)
оказалась
больше средней гармонической
.

При этом абсолютная
ошибка завышения составляет
— 2 км/ч (38 – 40), а относительная —5%

Т.о., неправильное
использование СА привело бы к завышению
средней скорости движения автомобиля
и к неправильному определению объема
перевозок. Это еще раз доказывает, с
какой осторожностью следует решать
вопрос о том, какую среднюю надлежит
применять в экономических расчетах.

В рассмотренном
примере частоты (веса) имели одно значение
и равнялись единице. Если же частоты
(веса) различные, то применяется СГ
взвешенная, которая
вычисляется следующим образом:

Где
–
СГ взвешенная:

Как первая, так и
вторая формулы показывают, что СГ есть
величина обратная СА.

Веса арифметической
средней и гармонической средней
обозначены разными буквами: f
и m.
Это не случайно, так как весами СА служат
частоты рассматриваемого ряда, а весами
СГ будет произведение вариантов на
веса.

Пример.
Рассмотрим данные о реализации товаров
по двум магазинам фирмы “Весна”
(табл. 6). Таблица
.6

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
29.05.20153.63 Mб107. Лекц.БУ-анализ.doc
#
18.12.2018130.46 Кб297.docx

Источник

Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину.
В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.
Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.

После того как составлена логическая формула можно пользоваться правилами (для простоты понимания упростим их и сократим):
1. Если в исходных данных (определяем по частоте) представлен знаменатель логической формулы, то расчет проводим по формуле средней арифметической взвешенной.
2. Если в исходных данных представлен числитель логической формулы, то расчет ведем по формуле средней гармонической взвешенной.
3. Если в задаче представлены сразу и числитель и знаменатель логической формулы (такое бывает редко), то расчет проводим по этой формуле или по формуле средней арифметической простой.
Это классическое представление о выборе верной формулы расчета средней величины. Далее представим последовательность действий при решении задач на расчет средней величины.

Алгоритм решения задач на расчет средней величины

А. Определяем способ расчета средней величины – простой или взвешенный. Если данные представлены в таблице то используем взвешенный способ, если данные представлены простым перечислением, то используем простой способ расчета.

Б. Определяем или расставляем условные обозначения – x – варианта, f – частота. Варианта это то, для какого явления требуется найти среднюю величину. Оставшиеся данные в таблице будут частотой.

В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот. Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»). Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).

Самое сложное, это догадаться, где и какое количество задано, особенно неопытному в таких делах студенту. В такой ситуации можно воспользоваться одним из предлагаемых далее способов. Для некоторых задач (экономических) подходит наработанное годами практики утверждение (пункт В.1). В других же ситуациях придется пользоваться пунктом В.2.

В.1 Если частота задана в денежных единицах (в рублях), то используется для расчета средняя гармоническая, такое утверждение верно всегда, если выявленная частота задана в деньгах, в других ситуациях это правило не действует.

В.2 Воспользоваться правилами выбора средней величины указанными выше в этой статье. Если частота задана знаменателем логической формулы расчета средней величины, то рассчитываем по средней арифметической форме, если частота задана числителем логической формулы расчета средней величины, то рассчитываем по средней гармонической форме.

Рассмотрим на примерах использование данного алгоритма.

Задача 1. Рассчитать средний размер пенсии, если известны пенсии 12 пенсионеров – 8500, 7900, 11200, 9900, 8800, 8700, 9100, 9500, 7500, 8400, 10400, 10600 рублей.

А. Так как данные представлены в строчку то используем простой способ расчета.

Б. В. Имеем только данные по величине пенсий, именно они и будут нашей вариантой – х. Данные представлены простым количеством (12 человек), для расчета используем среднюю арифметическую простую.

Средний размер пенсии пенсионера составляет 9208,3 рубля.

Задача 2. Рассчитать средний размер детских выплат по следующим данным

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.

Б. Так как требуется найти средний размер выплаты на одного ребенка, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.

В. Частота (число детей) задана явным количеством (можно подставить слово штук детей, с точки зрения русского языка неверное словосочетание, но, по сути, очень удобно проверять), значит, для расчета используется средняя арифметическая взвешенная.

Эту же задачу модно решить не формульным способом, а табличным, то есть занести все данные промежуточных расчетов в таблицу.

В результате все, что нужно теперь сделать, это разделить два итоговых данных в правильно порядке.

Средний размер выплаты на одного ребенка в месяц составил 1910 рублей.

Задача 3. Рассчитать среднюю себестоимость единицы изделия

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.

Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.

В. Частота (себестоимость выпуска) задана неявным количеством (частота задана в рублях пункт алгоритма В1), значит, для расчета используется средняя гармоническая взвешенная. Вообще же, по сути, себестоимость выпуска это сложный показатель, который получается перемножение себестоимости единицы изделия на количество таких изделий, вот это и есть суть средней гармонической величины.

Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо себестоимости выпуска стояло число изделий с соответствующей себестоимостью.

Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 410 (120+80+210) это и есть общее количество выпущенных изделий.

Средняя себестоимость единицы изделия составила 314,4 рубля.

Задача 4. Рассчитать среднюю число пропусков одного студента

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.

В. Частота (общее число пропусков) задана неявным количеством (это произведение двух показателей числа пропусков и числа студентов, имеющих такое количество пропусков), значит, для расчета используется средняя гармоническая взвешенная. Будем использовать пункт алгоритма В2.

Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо общего числа пропусков стояло число студентов.

Составляем логическую формулу расчета среднего числа пропусков одного студента.

Частота по условию задачи Общее число пропусков. В логической формуле этот показатель находится в числителе, а значит, используем формулу средней гармонической.

Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 31 (18+8+5) это и есть общее количество студентов.

Среднее число пропусков одного студента 13,8 дня.

Может еще поучимся? Загляни сюда!

Источник

Загрузить PDF

Нужно вычислить средний возраст некоторой группы людей? Это довольно просто. Вычисления представляют собой трехэтапный процесс, который легко понять и запомнить.

1

Составьте список всех возрастов. Вычислить среднее значение довольно легко. В вычислениях нужно учесть все числа набора данных. Поэтому запишите все числа (в данном случае возрасты) или внесите их в таблицу.^[1]
2

Найдите сумму всех записанных возрастов. Для этого сложите все числа. Например, рассмотрим группу из пяти человек следующих возрастов: 31, 30, 26, 21, 10. Сумма этих чисел равна 118.^[2]
3
Разделите полученную сумму на количество чисел (возрастов). Так вы найдете средний возраст. В нашем примере разделите 118 (сумма всех возрастов) на 5 (количество возрастов в списке). Средний возраст составит 23,6.
- Этот метод применим к набору данных с любым количеством чисел. Например, нужно найти средний возраст членов клуба. Допустим, что в клуб вступили 100 человек. Необходимо выяснить точный возраст каждого члена клуба. Сложите все возрасты, чтобы получить их сумму. Затем эту сумму разделите на 100, чтобы вычислить средний возраст членов клуба.
4
Найдите среднее значение других величин. С помощью описанного метода можно найти среднее значение любой величины, а не только средний возраст.
- Например, нужно узнать среднее население 10 крупнейших городов России. Необходимо определить количество жителей в каждом городе. Затем сложите найденные числа, а сумму разделите на 10, чтобы вычислить среднее население.
- Иногда вычисляют средневзвешенное значение. Например, при усреднении оценок учащегося оценки по некоторым предметам считаются важнее других.^[3] Чтобы вычислить средневзвешенное значение, умножьте каждое число на значимость его вклада (вес). Сложите полученные значения, а сумму разделите на общее количество чисел.^[4]
Реклама

1
Запомните отличие среднего значения от медианы. Некоторые люди не видят разницы между средним значением и медианой набора чисел. На самом деле в некоторых случаях лучше вычислить медиану, а не среднее значение.
- Медиана – это некоторое число набора данных, которое больше одной половины чисел набора данных и меньше другой половины чисел набора данных. То есть это число (в нашем случае возраст), которое делит набор чисел на две равные части.^[5].
- Медиана может быть лучшей оценкой возраста группы, если в группе есть выброс (аномальное число). Допустим, что возраст группы студентов университета лежит в пределах от 18 до 25 лет, а возраст одного студента равен 80 годам. Если вычислить среднее значение, престарелый студент исказит средний возраст группы, то есть группа окажется старше, чем на самом деле. Если же найти число, которое находится посередине группы чисел (возрастов), оно лучше охарактеризует возраст студентов. Поэтому вычисляйте медиану, если в наборе чисел присутствует выброс.
2
Запомните отличие среднего значения от моды. Мода – это число, которое встречается в группе чисел чаще всего.
- В некоторых случаях целесообразно вычислить среднее значение и моду или среднее значение и медиану.
- Если нужно найти средний возраст, но даны только диапазоны возрастов (например, определенное количество детей в возрасте от 2 до 4 лет и от 4 до 6 лет), вычислите среднее значение для каждого диапазона, сложите полученные числа, а сумму разделите на общее количество детей в каждом возрастном диапазоне.^[6]
Реклама

1
Воспользуйтесь электронной таблицей Excel. Чтобы вычислить средний возраст большой группы людей, внесите все возрасты в таблицу Excel. В противном случае (если вы пользуетесь только бумагой, ручкой и калькулятором) на такое вычисление уйдет много времени.
- Допустим, необходимо найти средний возраст всех учеников школы или работников крупной компании. В этом случае возрастов будет так много, что лучше воспользоваться программой для работы с электронными таблицами, такой как Excel.
- Сначала введите все возрасты в ячейки электронной таблицы Excel. Excel входит в пакет Microsoft Office. Либо введите возрасты вручную, либо импортируйте в Excel документ со всеми возрастами. Возможно, возрасты уже внесены в таблицу Excel.
- Чтобы импортировать текстовый файл в Excel, нажмите «Получить внешние данные» – «Из текста». Откроется мастер импортирования данных из внешнего документа в электронную таблицу.^[7]
2
Используйте формулу Excel, чтобы найти среднее значение. Предположим, возраст введен в ячейки столбца A в строках с 1 по 200. (Столбцы объединяют ячейки, которые расположены вертикально, а строки – ячейки, которые расположены горизонтально.) Чтобы вычислить среднее значение, нужно ввести соответствующую формулу Excel. Ее можно ввести в ячейке A201.
- Формула для вычисления среднего значения в Excel: =(СРЗНАЧ)A1:A200.^[8] Здесь вместо A1 нужно подставить адрес ячейки с первым возрастом. В нашем примере первый возраст находится в ячейке A1, потому что введен в первом столбце и первой строке. Вместо A200 нужно подставить адрес ячейки с последним возрастом.
- В нашем примере последний возраст находится в ячейке A200, потому что введен в первом столбце и двухсотой строке. Двоеточие между адресами двух ячеек указывает программе, что нужно сложить все числа, находящиеся в ячейках с А1 по А200, а затем найти среднее значение этой суммы. Нажмите Enter, чтобы в ячейке А201 отобразился средний возраст.
3
Воспользуйтесь онлайн-калькулятором. В интернете есть сервисы, которые упрощают вычисление среднего значения. Такие сервисы снабжены онлайн-калькуляторами, в которые вводится набор чисел.^[9]
- Конечно, можно пользоваться карандашом, бумагой и обычным калькулятором. Как только вы поймете, как работает формула для вычисления среднего значения, вы с легкостью определите, чем пользоваться в процессе вычислений.
Реклама

Советы

Работая в Excel, не трогайте исходную таблицу с данными; сделайте копию и редактируйте ее. Это необходимо на тот случай, если вы запутаетесь или захотите проверить вычисления.

Об этой статье

Эту страницу просматривали 78 373 раза.

Была ли эта статья полезной?

Источник

Примеры решения задач

Пример 1

Пример 2

Пример: вычислить среднее значение по дате в Excel

Дополнительные ресурсы

Средняя хронологическая

Данные для расчета средней численности сотрудников компании “Бест”

Средняя гармоническая (сг).

Алгоритм решения задач на расчет средней величины

Может еще поучимся? Загляни сюда!

Советы

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Svchost exe что это за процесс windows 7 грузит память как исправить

Как найти фильм петля времени

0x8000ffff как исправить эту ошибку

Добавить комментарий Отменить ответ