- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Построения циркулем и линейкой
- Среднее пропорциональное
Среднее пропорциональное положительных чисел 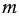 и
и 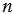 – это такое число
– это такое число 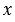 , которое равно квадратному корню из произведения этих чисел, т.е.
, которое равно квадратному корню из произведения этих чисел, т.е. 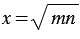 .
.
Среднее пропорциональное носит такое название, потому что число 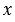 является средним членом пропорции
является средним членом пропорции 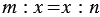 .
.
Средним пропорциональным (или средним геометрическим) двух отрезков 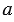 и
и 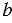 , называется такой отрезок
, называется такой отрезок 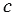 , что:
, что: 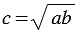 .
.
Чтобы построить среднее пропорциональное двух отрезков используют циркуль и линейку.
Ход построения:
Пусть нам даны два отрезка 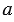 и
и 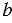 , строим их.
, строим их.
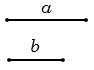
Затем строим с помощью линейки прямую 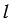 , отмечаем на ней точку А и строим отрезок АЕ, равный отрезку
, отмечаем на ней точку А и строим отрезок АЕ, равный отрезку 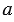 . Для этого строим с помощью циркуля окружность радиуса
. Для этого строим с помощью циркуля окружность радиуса 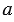 с центром А (полностью окружность строить необязательно, смотри выделенное красным цветом). Затем, аналогично строим отрезок ЕВ, равный отрезку
с центром А (полностью окружность строить необязательно, смотри выделенное красным цветом). Затем, аналогично строим отрезок ЕВ, равный отрезку 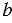 .
.
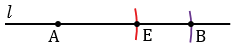
Далее найдем середину отрезка АВ. Для этого строим две окружности с центрами А и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая пересечет отрезок АВ в его середине О.
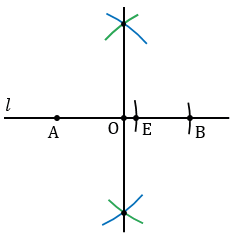
Теперь строим окружность с центром О радиуса ОА.
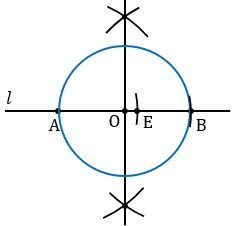
Затем построим перпендикуляр к прямой 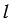 так, чтобы он проходил через точку Е, которая делит отрезок АВ в отношении
так, чтобы он проходил через точку Е, которая делит отрезок АВ в отношении 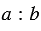 . Для этого строим окружность произвольного радиуса с центром Е (полностью окружность строить необязательно, смотри выделенное фиолетовым цветом), данная окружность пересечет прямую
. Для этого строим окружность произвольного радиуса с центром Е (полностью окружность строить необязательно, смотри выделенное фиолетовым цветом), данная окружность пересечет прямую 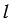 в двух точках М и В (точку В мы берем как точку пересечения данной окружности и данной прямой для того, чтобы не добавлять на рисунке лишние элементы, но важно помнить, что точки пересечения окружности с центром Е и прямой
в двух точках М и В (точку В мы берем как точку пересечения данной окружности и данной прямой для того, чтобы не добавлять на рисунке лишние элементы, но важно помнить, что точки пересечения окружности с центром Е и прямой 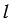 могут быть и другие, все зависит от того, каким мы возьмем радиус окружности с центром Е). Далее строим две окружности с центрами М и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая будет перпендикулярна к прямой
могут быть и другие, все зависит от того, каким мы возьмем радиус окружности с центром Е). Далее строим две окружности с центрами М и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая будет перпендикулярна к прямой 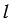 и пересечет окружность с центром О в точке К.
и пересечет окружность с центром О в точке К.
Длина отрезка ЕК и есть искомый отрезок 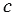 , равный среднему пропорциональному отрезков
, равный среднему пропорциональному отрезков 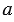 и
и 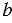 , т.е.
, т.е. 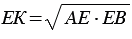 или
или 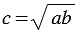 .
.
Советуем посмотреть:
Построение угла, равного данному
Построение биссектрисы угла
Построение перпендикулярных прямых
Построение середины отрезка
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 1270,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Среднее пропорциональное
- Среднее пропорциональное
-
между двумя положительными числами, число, равное квадратному корню из их произведения. Таким образом, если а: х = х: b, то x есть С. п. чисел а и b и
 х называется также геометрическим средним чисел а и b.
х называется также геометрическим средним чисел а и b.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
Смотреть что такое “Среднее пропорциональное” в других словарях:
-
СРЕДНЕЕ ПРОПОРЦИОНАЛЬНОЕ — между двумя положительными числами a и b число x, равное квадратному корню из их произведения … Большой Энциклопедический словарь
-
среднее пропорциональное — между двумя положительными числами a и b, число x, равное квадратному корню из их произведения: . * * * СРЕДНЕЕ ПРОПОРЦИОНАЛЬНОЕ СРЕДНЕЕ ПРОПОРЦИОНАЛЬНОЕ между двумя положительными числами a и b, число x, равное квадратному корню из их… … Энциклопедический словарь
-
СРЕДНЕЕ ПРОПОРЦИОНАЛЬНОЕ — см. Геометрическое среднее … Естествознание. Энциклопедический словарь
-
Среднее пропорциональное — … Википедия
-
Среднее геометрическое — Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось. Более формально: Среднее геометрическое двух чисел также называется… … Википедия
-
Прямоугольный треугольник — Прямоугольный треугольник это треугольник, в котором один угол прямой (то есть составляет 90 градусов). Соотношения между сторонами и … Википедия
-
СРЕДНИЙ — и (устар., простореч.) середний, средняя, среднее. 1. Равно удаленный от начала и конца или находящийся вообще между какими н. крайними пространственными или временными точками, находящийся, стоящий между двумя какими н. предметами, величинами и… … Толковый словарь Ушакова
-
Орезм — [(иногда называемый Orem, Horem, Horen), Николай, иногда Жак)] французский математик (1323 1382). В 1348 г. поступил в наваррскую коллегию в Париже. По окончании курса О. оставался в коллегии сначала в должности учителя, а затем начальника до… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
-
АРХИТ — (Ἀρχύτας) (4 в. до н.э.) – древнегреч. философ, пифагореец; родом из Тарента, глава его правительства; друг Платона. А. – автор многих соч., от к рых дошло лишь неск. фрагментов. Ставя вопрос: Если бы я находился на самом крае вселенной, смог ли… … Философская энциклопедия
Лучший ответ
Евгений Кутузов
Просветленный
(49079)
6 лет назад
√(ab) – среднее пропорциональное (или среднее геометрическое).
(a + b) / 2 – это среднее арифметическое.
Остальные ответы
Зри Корень
Мыслитель
(6782)
6 лет назад
(а+б) 2 или (а+б+с) 3 Вообщем берешь складываешь тупо все числа и делишь на их количество!
vsch8
Просветленный
(32482)
6 лет назад
у 2 чисел только среднее
Вега
Искусственный Интеллект
(122860)
6 лет назад
(А+в) ÷2
Мария Шевцова
Мастер
(2072)
6 лет назад
Среднее пропорциональное-это сумма чисел/букв, деленная на то число, сколько присутствует этих чисел/букв
К примеру:
(6+9+3)/3=6.
(9+6+4+1)/4=5
(5+5+3+2+1)/5=3
(120+30+50+10+40)/5=50
Getting confused while solving the mean proportional problems then practice more with this Mean Proportional Worksheet pdf and learn the concept of mean proportional efficiently. Mean proportional is also known as Geometric Mean and it is not similar to the arithmetic mean. The Mean Proportion is calculated between two terms of a ratio by taking the square root of the product of those two quantities in terms of ratio.
Let us understand more about mean proportional by taking help from this free printable mean proportional of two numbers worksheet. For example, if a, b, and c are in continued proportion then b is called the mean proportional of a and c. The mean proportion is expressed as b = √ac. This free printable Worksheet on Mean Proportional with Answers PDF helps you understand the problem-solving techniques and feels fun to practice.
Also Read:
- Worked out Problems on Ratio and Proportion
- Worksheet on Proportions
- Worksheet on Proportion and Continued Proportion
Mean Proportional Worksheet PDF with Solutions
Example 1:
Find the mean proportional of the following sets of positive integers:
(i) x- y, x³- x²y
(ii) x³y, xy³
Solution:
(i) Given x- y, x³- x²y
Now, to find the mean proportion.
Let p be the mean proportional between x- y, x³- x²y.
So, x- y: p:: p: x³- x²y
Product of extremes = Product of means.
Now,
p² = (x- y)(x³- x²y)
⇒ p² = x²(x- y)(x- y)
⇒ p² = x²(x- y)²
⇒ p = √(x²(x- y)²)
⇒ p = x(x- y)
Thus, the mean proportion of x- y, x³- x²y is x(x- y).
(ii) Given x³y, xy³
Let m be the mean proportion of x³y, xy³.
So, x³y: m:: m: xy³.
Product of extremes = Product of means.
Product of extremes = x³y × xy³
Product of means = m × m = m²
m² = x³y × xy³
⇒ m² = (x³ × x) × (y³ × y)
⇒ m² = x4 × y4
⇒ m = √(x4 × y4)
⇒ m = √(x²y²)²
⇒ m = x²y²
Hence, the mean proportion of x³y, xy³ is x²y².
Example 2:
Find the mean proportional of the following:
(i) 8 and 32
(ii) 0.04 and 0.56
(iii) 4 and 25
Solution:
(i) Given 8 and 32
Let the mean proportion between 8 and 32 is a.
Now, 8: a:: a: 32
We know that, Product of extremes = Product of means.
Here, extremes are 8 and 32 and means are a and a.
So, 8 × 32 = a × a
⇒ a² = 256
⇒ a = √256
⇒ a = 16
Thus, the value of mean proportion ‘a’ is 16.
(ii) Given 0.04 and 0.56
Let the mean proportion be p.
Now, 0.04: p:: p: 0.56
We know that, Product of extremes = Product of means.
The extremes are 0.04 and 0.56 and the means are p and p.
So, 0.04 × 0.56 = p × p
⇒ p² = 0.02
⇒ p = √0.02
⇒ p = 0.14
Therefore, the value of the mean proportion p is 0.14.
(iii) Given 4 and 25
Let the mean proportion between 4 and 25 be x.
Thus, 4: x:: x: 25
We know that, Product of extremes = Product of means.
Here, the extremes are 4 and 25 and the means are x and x.
So, 4 ×25 = x × x
⇒ x² = 100
⇒ x = √100
⇒ x = 10
Hence, the mean proportion of 4 and 25 is 10.
Go through topicwise concepts and worksheets from 10th Grade Math for free and learn math in a fun and interactive manner.
Example 3:
If b is the mean proportion between a and c, show that a4+ a2b2+ b4/b4+ b2c2+ c4 = (frac{a²}{c²}).
Solution:
Given b is the mean proportion between a and c, then we have b² = ac.
Now, we have to prove that a4+ a2b2+ b4 / b4+ b2c2+ c4 = (frac{a²}{c²}) i.e., L.H.S = R.H.S.
LHS = a4+ a2b2+ b4/ b4+ b2c2+ c4
Let us substitute b² = ac in LHS.
LHS = a4+ a²(ac)+ (ac)²/(ac)²+ (ac)c²+ c4
⇒ LHS = (frac{a²( a²+ ac+ c² )}{c²( a²+ ac+ c² )})
⇒ LHS = (frac{a²}{c²}) = RHS
⇒ LHS = RHS
Therefore, a4+ a2b2+ b4/ b4+ b2c2+ c4= (frac{a²}{c²}).
Example 4:
Find the mean proportion of the following
(i) 4(frac{4}{5}), 2(frac{1}{2})
(ii) a²b, ab²
Solution:
(i) Given 4(frac{4}{5}), 2(frac{1}{2})
Now, change the mixed fraction into proper fraction
4(frac{4}{5}) = (frac{24}{5})
2(frac{1}{2}) = (frac{5}{2})
Let m be the mean proportion of (frac{24}{5}), (frac{5}{2}).
Product of extremes = Prouct of means
Here, the extremes are (frac{24}{5}) and (frac{5}{2}), the means are m and m.
(frac{24}{5}) × (frac{5}{2}) = m × m
⇒ m² = (frac{24}{2})
⇒ m² = 12
⇒ m = √12
⇒ m = 3.46
Thus, the value of mean proportion is 3.46.
(ii) Given a²b, ab²
Let k be the mean proportion of a²b and ab².
So, a²b: k:: k: ab².
In mean proportion, Product of extremes = Product of means.
Now, a²b × ab² = k²
⇒ k² = a³b³
⇒ k² = (ab)¹ × (ab)²
⇒ k = √((ab)¹)²
⇒ k = ab
Therefore, ab is the mean proportion of a²b, ab².
