Планиметрия
6. Подобие фигур
6.7. Средние пропорциональные отрезки в прямоугольном треугольнике
Когда говорят о среднем пропорциональном отрезке между двумя данными отрезками
и
, то имеют в виду следующее соотношение между их длинами (числами) :
или
.
Теоремы
Если в прямоугольном треугольнике опущена высота на гипотенузу, то:
1) высота является средним пропорциональным между проекциями катетов на гипотенузу;
2) каждый из катетов есть среднее пропорциональное между всей гипотенузой и его проекцией на гипотенузу.
Дано : ,
,
.
Требуется доказать:
1) ;
2) ;
.
Доказательство:
1) , так как у них имеется по прямому углу и
(углы с соответственно перпендикулярными сторонами). Катет
в
сходственен катету
в
(лежат против равных углов) и другие катеты
и
этих треугольников также сходственны. В подобных треугольниках отношения сходственных сторон равны:
,
.
2) (они прямоугольные и
общий). Сходственны их гипотенузы
и
, а также катеты, прилежащие к общему углу,
и
:
;
.
Аналогично рассматриваем подобные треугольники и
, из которых получаем, что
.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Пропорциональные отрезки в прямоугольном треугольнике
Задача
Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Дано:  АВС – прямоугольный,
АВС – прямоугольный,  С – прямой, СD – высота.
С – прямой, СD – высота.
Доказать:  АВС
АВС
 АСD,
АСD,  АВС
АВС
 СВD,
СВD,  АСD
АСD
 СВD.
СВD.
Доказательство:
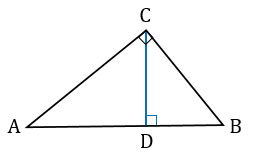
1. В  АВС и
АВС и  АСD:
АСD:  А – общий,
А – общий,  АСВ =
АСВ = АDС = 900, следовательно,
АDС = 900, следовательно,  АВС
АВС
 АСD (по 1 признаку подобия треугольников).
АСD (по 1 признаку подобия треугольников).
2. В  АВС и
АВС и  СВD:
СВD:  В – общий,
В – общий,  АСВ =
АСВ = ВDС = 900, следовательно,
ВDС = 900, следовательно,  АВС
АВС
 СВD (по 1 признаку подобия треугольников), поэтому из определения подобных треугольников следует, что
СВD (по 1 признаку подобия треугольников), поэтому из определения подобных треугольников следует, что  АСВ =
АСВ = ВDС.
ВDС.
3. В  АСD и
АСD и  СВD:
СВD:  АСВ =
АСВ = ВDС,
ВDС,  АDС =
АDС = ВDС = 900, следовательно,
ВDС = 900, следовательно,  АСD
АСD
 СВD (по 1 признаку подобия треугольников). Что и требовалось доказать.
СВD (по 1 признаку подобия треугольников). Что и требовалось доказать.
Средним пропорциональным (или средним геометрическим) двух отрезков АВ и СD, называется такой отрезок ХY, что: 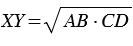 .
.
Утверждения:
Доказательство
Дано:  АВС – прямоугольный,
АВС – прямоугольный,  С – прямой, СD – высота, АВ – гипотенуза.
С – прямой, СD – высота, АВ – гипотенуза.
Доказать: 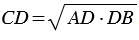 .
.
Доказательство:

 АСD
АСD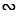
 СВD (доказательство данного утверждения приведено в задаче выше), поэтому сходственные стороны данных треугольников пропорциональны, т.е.
СВD (доказательство данного утверждения приведено в задаче выше), поэтому сходственные стороны данных треугольников пропорциональны, т.е. 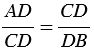 , откуда,
, откуда, 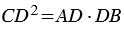 , тогда
, тогда 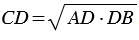 . Что и требовалось доказать.
. Что и требовалось доказать.
Доказательство
Дано:  АВС – прямоугольный,
АВС – прямоугольный,  С – прямой, СD – высота, АВ – гипотенуза.
С – прямой, СD – высота, АВ – гипотенуза.
Доказать: 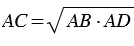 ,
, 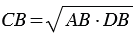 .
.
Доказательство:

1. В  АВС и
АВС и  АСD:
АСD:  А – общий,
А – общий,  АСВ =
АСВ = АDС = 900, следовательно,
АDС = 900, следовательно,  АВС
АВС
 АСD (по 1 признаку подобия треугольников), поэтому сходственные стороны данных треугольников пропорциональны, т.е.
АСD (по 1 признаку подобия треугольников), поэтому сходственные стороны данных треугольников пропорциональны, т.е. 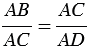 , откуда
, откуда 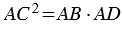 , тогда
, тогда 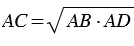 .
.
2. В  АВС и
АВС и  СВD:
СВD:  В – общий,
В – общий,  АСВ =
АСВ = ВDС = 900, следовательно,
ВDС = 900, следовательно,  АВС
АВС
 СВD (по 1 признаку подобия треугольников), поэтому сходственные стороны данных треугольников пропорциональны, т.е.
СВD (по 1 признаку подобия треугольников), поэтому сходственные стороны данных треугольников пропорциональны, т.е. 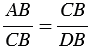 , откуда
, откуда 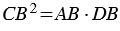 , тогда
, тогда 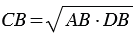 . Что и требовалось доказать.
. Что и требовалось доказать.
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 572,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 573,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 574,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 575,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 577,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 578,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 668,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 669,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 855,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 868,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Признак подобия прямоугольных треугольников
Признак подобия треугольников с прямым углом является частным случаем первого признака подобия треугольников, который предполагает следующее: при соответствии двух углов одного треугольника двум углам другого такие треугольники являются подобными.
Теорема
Формулировка для треугольников с углами в 90°: подобие прямоугольных треугольников имеет место, когда острый угол одного треугольника является равным острому углу другого.
Рассмотрим наглядно на схеме:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
∠C=∠C1=90°
∠A=∠A1
∠B=180°−(∠C+∠A)
∠B1=180°−(∠C1+∠A1)
Отсюда следует, что ΔABC∼ΔA1B1C1.
Примечание
Сумма острых углов прямоугольного треугольника равна 90°.
Пропорциональные отрезки в прямоугольном треугольнике — отношение
Определение
Средним пропорциональным двух величин a и b называется число c при условии, что квадрат c равен произведению a и b, то есть c2=ab.
На рисунке изображен прямоугольный треугольник с катетами a и b, гипотенузой c и проведенной к ней высоте h. Высота делит гипотенузу на два отрезка: ac и bc, именуемые проекциями катетов на гипотенузу.
Теорема 1
Среднее пропорциональное между гипотенузой и проекцией на нее – это каждый катет прямоугольного треугольника, то есть:
(a^2=a_ctimes c )
(b^2=b_ctimes c)
Доказательство
Пусть в ΔABC ∠C=90°, ∠A=α, CH – высота.
1. Сначала докажем, подобие ΔABC и ΔCBH.
Поскольку CH – высота, то ∠CHB равен 90°.
∠B=90°−α – это общий угол рассматриваемых треугольников ABC и CBH.
∠HCB=90°−∠B=90°−(90°−α)=α.
Следовательно, в ΔABC и ΔCBH:
∠ACB=∠HCB=90°
∠B – общий и равен 90°−α
∠CAB=∠HCB=α
Отсюда следует, что ΔABC∼ΔCBH.
2. Теперь докажем, что ΔABC∼ΔACH.
∠ACB=∠AHC=90°, т.к. СН – высота ΔABC.
∠A – общий и равен α.
∠ACH=90−α, а значит, равен ∠AВC.
Следовательно, ΔABC∼ΔACH.
3. Сделаем на схеме дополнительные обозначения проекций катетов:
4. Применим доказанное подобие ΔABC и ΔCBH и запишем пропорции сторон:
(frac ac=frac{a_c}a)
В переводе с математического языка это означает следующее: отношение противолежащих прямому углу сторон, ровняется отношению сторон, расположенных напротив угла α. Из данного соотношения получается:
((1)a^2=a_ctimes c)
5. Воспользуемся тем, что ΔABC∼ΔACH. Запишем пропорции сторон:
(frac bc=frac{b_c}b)
Это значит, что отношение сторон, противолежащих прямому углу равно отношению сторон, лежащих напротив α. Выведем из пропорции следующее уравнение:
((2)b^2=b_ctimes c)
Полученные равенства (1) и (2) доказывают теорему.
Теорема 2
Средним пропорциональным между проекциями катетов является высота, опущенная на гипотенузу из вершины угла в 90°, то есть при умножении отрезков ac и bc получается величина, равная квадрату высоты:
(h^2=a_ctimes b_c)
Доказательство:
Поскольку ранее мы доказали подобия треугольников ΔABC∼ΔCBH и ΔABC∼ΔACH, то ΔCBH∼ΔACH. Используем этот факт для доказательства второй теоремы. Запишем пропорцию:
(frac h{a_c}=frac{b_c}h)
Она значит, что отношение сторон, противолежащих углу (90°−α), равно соотношению сторон, противолежащих углу α.
Выведем отсюда значение h:
(h^2=a_ctimes b_c)
Теорема доказана.
Следствие
Гипотенуза разделена высотой на отрезки, соотношение которых равно отношению квадратов катетов. В виде формулы это свойство выглядит так:
(frac{a_c}{b_c}=frac{a^2}{b^2})
Альтернативное доказательство теоремы Пифагора
Сформулированные и доказанные теоремы позволяют привести альтернативу традиционному доказательству пифагоровой теоремы:
(left.begin{array}{r}b^2=b_ctimes c\a^2=a_ctimes cend{array}right}Rightarrow a^2+b^2=a_ctimes c+b_ctimes c=cleft(a_c+b_cright)=ctimes c=c^2)
Примеры решения задач на использование пропорциональных отрезков в прямоугольном треугольнике
Задача 1
В ΔABC: ∠С=90°, СН – высота, отрезок АН=9 см, отрезок АН=16 см. Вычислите длину катетов и высоты треугольника ABC.
Решение
- Определим длину гипотенузы: AB=9+16=25 см.
- Применим доказанные теоремы:
(BC=sqrt{ABtimes BH}=sqrt{25times16}=5times4=20)
(AC=sqrt{ABtimes AH}=sqrt{25times9}=5times3=15)
(CH=sqrt{BHtimes AH}=sqrt{16times9}=4times3=12)
Ответ: сторона ВС=20 см, сторона АС=15 см, высота СН=12 см.
Задача 2
В прямоугольном треугольнике ABC сторона АС равна 8 см, сторона AB равна 10 см. Вычислить длину высоты CD.
Решение
1. Так как треугольники АВС и АСD подобны, можно составить пропорции сторон:
(frac{AB}{AC}=frac{BC}{CD})
2. Найдем длину катета ВС:
(BC=sqrt{AB^2-AC^2}=sqrt{10^2-8^2}=sqrt{100-64}=36=6)
(ВС=6) см
3. Далее подставим полученную величину в соотношение, записанное в первом пункте:
(frac{10}8=frac6{CD})
Теперь выведем отсюда уравнение с неизвестным CD:
(CD=frac{8times6}{10}=frac{48}{10}=4,8)
Ответ: CD=4,8 см.
Пропорциональные отрезки в прямоугольном треугольнике
В этом уроке познакомимся с понятием «среднее геометрическое» или «среднее пропорциональное» для отрезков, выведем формулы для вычисления высоты и катетов прямоугольного треугольника через понятие среднее пропорциональное, рассмотрим задачу на применение формул.
Решим задачу:
Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Дано:
∆АВС – прямоугольный треугольник,
СD – высота, проведенная из вершины С к гипотенузе АВ.
Доказать:
∆АВС ~ ∆АСD;
∆АВС ~ ∆CBD
∆АСD ~ ∆CBD.
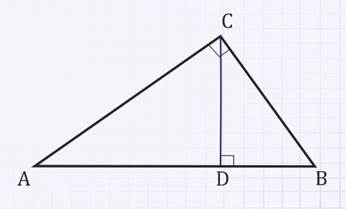
Доказательство:
1)Рассмотрим треугольники АВС и АСD.
Так как ∠А–общий,
∠АСВ = ∠АDС = 90°, отсюда следует, что треугольники АВС и АСD подобны по первому признаку подобия треугольников, т.е. по двум равным углам.
2)Рассмотрим треугольники АВС и СВD.
Так как ∠В–общий,
∠АСВ = ∠ВDС = 90°, то треугольники АВС и СВD тоже подобны по первому признаку подобия треугольников. А раз так, то ∠А = ∠ВСD.
3)Рассмотрим треугольники АСD и СВD.
Так как ∠АDС = ∠СDВ = 90° и ∠А = ∠ВСD, то треугольники АСD и СВD подобны по первому признаку подобия треугольников.
Что и требовалось доказать.
В геометрии в формулировках ряда утверждений и при решении отдельных задач используется понятие «среднее пропорциональное отрезков» или «среднее геометрическое».
Отрезок ХУ называется средним пропорциональным (или средним геометрическим) для отрезков АВ и СD, если выполняется равенство:
![]()
Исходя из доказанной выше задачи, можно выделить два утверждения.
1.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
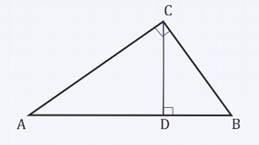
Для вывода данного утверждения воспользуемся доказанным, а именно, что:
![]()
поэтому:
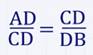
Применяя основное свойство пропорции, получим
![]()
2.Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Также по выше доказанному в задаче:
![]()
поэтому:
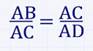
и, следовательно:
![]()
Решим задачу, применяя данные утверждения.
Задача:
Найдите катеты прямоугольного треугольника АВС, если АD = 24 см, ВD = 6 см.
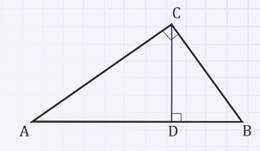
Решение:
Найдем гипотенузу данного прямоугольного треугольника:
![]()
Теперь воспользуемся равенством второго утверждения:
![]()
Для вычисления второго катета воспользуемся теоремой Пифагора:
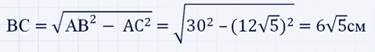
или равенством все того же второго утверждения:
![]()
Начнём с повторения уже известных нам сведений о
прямоугольном треугольнике.
Прямоугольным называется треугольник,
у которого один из углов прямой.
Сторону, лежащую против прямого угла, называют гипотенузой,
а две другие — катетами.
Вы уже знакомы с очень важной теоремой, теоремой
Пифагора. Она гласит, что в прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов.
А также вам известны признаки равенства
прямоугольных треугольников. Они могут быть равны: по двум катетам, по катету и
прилежащему к нему углу, по гипотенузе и острому углу, по катету и гипотенузе.
Сегодня поговорим о пропорциональных отрезках в
прямоугольном треугольнике. И начнём с задачи.
Задача. Докажите, что
высота прямоугольного треугольника, проведенная из вершины прямого угла,
разделяет треугольник на два подобных прямоугольных треугольника, каждый из
которых подобен данному треугольнику.
Доказательство.
1.
2.
3.
Так мы доказали, что высота прямоугольного
треугольника, проведенная из вершины прямого угла, разделяет треугольник на два
подобных прямоугольных треугольника, каждый из которых, в свою очередь, подобен
данному треугольнику.
Определение.
Отрезок называется
средним пропорциональным
(или средним геометрическим) для отрезков и
,
если .
Опираясь на данное определение и задачу, решённую нами, докажем
следующие утверждения:
высота прямоугольного треугольника, проведенная из
вершины прямого угла, есть среднее пропорциональное для отрезков, на которые
делится гипотенуза этой высотой.
В предыдущей задаче нами уже было доказано, что
треугольники
катет прямоугольного треугольника есть среднее
пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между
катетом и высотой, проведенной из вершины прямого угла.
Докажем второе утверждение.
Для этого воспользуемся подобием треугольников ABC
и ACD. Запишем отношение
соответствующих сторон.
Отсюда получаем, что АЦ равно корню квадратному из
произведения АБ и АД.
Выполним задание.
Задача. Найдите элементы
прямоугольного треугольника по известным данным.
а)
б)
в)
г)
Решение.
а)
б)
в)
г)
Задача. По данным
рисунка нужно найти площадь .
Решение.
а)
1.
2.
3.
б)
1.
2.
3.
4.
Ответ: а) , б)
.
Задача. —
ромб, равно
12, .
Найдите площадь ромба.
Решение.
1.
2. Пусть
3.
4.
Ответ: .
Подведём итоги урока.
Сегодня вы познакомились с определением среднего
геометрического и узнали, как это понятие связано с прямоугольным
треугольником.
А именно:
Высота прямоугольного треугольника, проведенная из
вершины прямого угла, есть среднее пропорциональное для отрезков, на которые
делится гипотенуза этой высотой.
Катет прямоугольного треугольника есть среднее
пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между
катетом и высотой, проведенной из вершины прямого угла.
