2017-06-30 ![]()
Оцените среднее расстояние между молекулами воздуха при нормальных условиях.
Решение:
Известно, что один моль любого газа при нормальных условиях ($p_{0} = 1атм = 1,013 cdot 10^{5} Па$ и $t = 0^{ circ} С$,или $T_{0} = 273 К$) занимает объем
$V = 22,4 л$.
Так как в 1 моле вещества содержится $N_{A} = 6,022 cdot 10^{23}$ молекул, то объем пространства $V_{1}$, приходящийся на 1 молекулу,
$V_{1} = frac{V}{N_{A}} = frac{RT_{0}}{pN_{A}} = 3,72 cdot 10^{-26} м^{3}$.
Линейный размер $a$ ячейки пространства, приходящейся на 1 молекулу, равен (ячейку представляем в виде кубика):
$a = sqrt[3]{ V_{1}} = sqrt[3]{ frac{RT_{0}}{pN_{A}}} = 3,34 cdot 10^{-8} м$.
Эта величина и может служить оценкой среднего расстояния между молекулами воздуха:
$ sim 3 cdot 10^{-8} м$.
Твердые тела
Атомы или молекулы
твердых тел в отличие от жидкостей не
могут разорвать свои связи с ближайшими
соседями и колеблются около определенных
положений равновесия. Правда, иногда
молекулы изменяют положение равновесия,
но происходит это крайне редко. Вот
почему твердые тела сохраняют не только
объем, но и форму.
Есть еще одно
различие между жидкими и твердыми
телами. Жидкость можно сравнить с толпой,
в которой люди беспокойно толкутся на
месте, а твердое тело, как правило,
подобно стройной когорте, где люди хотя
и не стоят по стойке «смирно», но
выдерживают между собой в среднем
определенные интервалы. Если соединить
центры положений равновесия атомов или
молекул твердого тела, то получится
правильная пространственная решетка,
называемая кристаллической. На рисунках
2.25 и 2.26 показаны кристаллические решетки
поваренной соли и алмаза*.
* В действительности
размеры атомов (или ионов) сравнимы с
расстояниями между узлами кристаллической
решетки, так что атомы почти соприкасаются
друг с другом. На рисунках 2.25 и 2.26 их
размеры сознательно уменьшены, для того
чтобы была видна кристаллическая
решетка.
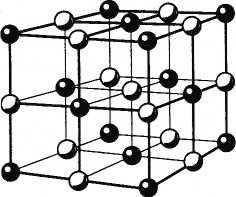
Рис. 2.25

Рис. 2.26
Если кристаллу не
мешают расти, то внутренний порядок в
расположении атомов приводит к
геометрически правильным внешним
формам.
Кривая
потенциальной энергии взаимодействия
молекулы твердого тела со своими
ближайшими соседями (рис. 2.27) похожа на
кривую потенциальной энергии взаимодействия
молекул жидкости (см. рис. 2.24). Только
глубина потенциальной ямы должна быть
несколько больше, так как молекулы
расположены ближе друг к другу. Условие
![]() ,
,
выполняемое
для жидких тел, выполняется и для твердых.
Но кинетическая энергия молекул твердого
тела значительно меньше, чем молекул
жидкости. Ведь твердые тела образуются
при охлаждении. Соответственно в твердых
телах средняя кинетическая энергия
молекул значительно меньше абсолютного
значения средней потенциальной энергии:
![]()
(2.6.3)
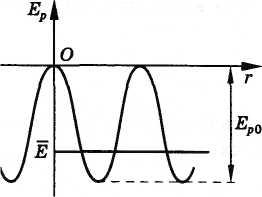
Рис. 2.27
На рисунке 2.27
средняя энергия молекулы внутри ямы
изображена отрезком прямой. Частица
совершает колебания у дна потенциальной
ямы. Высоты потенциальных барьеров
между соседними ямами велики, и молекулы
почти не перемещаются из одного положения
равновесия в другое. Для перемещения
молекула должна получить энергию,
значительно превышающую среднюю. Это
событие маловероятно. Вот почему твердые
тела в отличие от жидкостей сохраняют
свою форму.
У
газов
средняя кинетическая энергия молекул
больше средней потенциальной энергии.
У жидкостей средняя кинетическая энергия
немного меньше средней потенциальной,
у твердых тел средняя кинетическая
энергия много меньше средней потенциальной.
§ 2.7. Примеры решения задач
При
решении большей части задач на тему
«Основы молекулярно-кинетической
теории» нужно уметь определять молярные
массы вещества. Для этого по известным
из таблицы Д. И. Менделеева относительным
атомным массам надо определить
относительную молекулярную массу, а
затем и молярную массу по формуле М
=
10-3Мr
кг/моль, где М
— молярная
масса, Мr
—
относительная молекулярная масса.
Во
многих задачах требуется по известной
массе тела определить количество
вещества или число атомов (молекул) в
нем. Для этого используются формулы:
![]() и
и![]() .
.
Массы отдельных молекул определяются
по формуле:![]() .
.
В
некоторых задачах массу вещества нужно
выразить через его плотность р и объем
V:
т = pV.
Задача
1
В двух сосудах
находятся вода и ртуть одинакового
объема. Сравните число атомов в этих
жидкостях.
Решение.
Вода
содержит
![]() молекул или
молекул или![]() атомов, а ртуть содержит
атомов, а ртуть содержит![]()
атомов.
Масса
воды т1
= p1V;
масса ртути т2
=
p2V,
где
р1
= 1000 кг/м3
—
плотность воды, а р2
= 13 600 кг/т3
— плотность
ртути. Молярная масса воды М1
= 18·10-3
кг/моль; молярная масса ртути М2
=
0,2006 кг/моль. Следовательно,

Число атомов в
воде примерно в 25 раз больше, чем в ртути.
Задача
2
Определите
среднее расстояние d
между
центрами соседних молекул в куске льда.
Плотность льда р = 900 кг/м3.
Решение.
При
плотной упаковке молекул среднее
расстояние d
между
центрами соседних молекул равно линейным
размерам самих молекул. Поэтому
![]()
где
V
— объем
куска льда, а N
— число
молекул в нем.
Согласно
(2.2.7)
![]() .
.
Поэтому
![]()
Отсюда
![]()
Задача
3
Вычислите
примерные размеры атома золота.
Решение.
Объем
одного моля золота равен
![]() ,
,
где p = 1,93·104
кг/м3
— плотность золота, М
= 0,197
кг/моль — его молярная масса. Объем
одного атома золота равен

Пренебрегая
промежутками между атомами ввиду их
плотной упаковки, найдем приближенно
линейный размер атома:
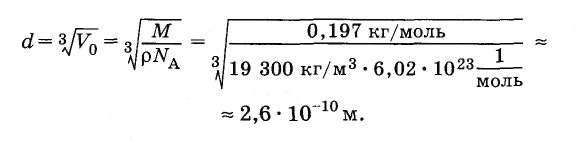
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условие задачи:
Чему равно среднее расстояние между молекулами насыщенного водяного пара при температуре 100° C?
Задача №4.1.65 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(t=100^circ) C, (l-?)
Решение задачи:
 Рассмотрим водяной пар в некотором произвольном количестве, равном (nu) моль. Чтобы определить объем (V), занимаемый данным количеством водяного пара, нужно воспользоваться уравнением Клапейрона-Менделеева:
Рассмотрим водяной пар в некотором произвольном количестве, равном (nu) моль. Чтобы определить объем (V), занимаемый данным количеством водяного пара, нужно воспользоваться уравнением Клапейрона-Менделеева:
[pV = nu RT]
[V = frac{{nu RT}}{p}]
В этой формуле (R) – универсальная газовая постоянная, равная 8,31 Дж/(моль·К). Давление насыщенного водяного пара (p) при температуре 100° C равно 100 кПа, это известный факт, и его должен знать каждый учащийся.
Чтобы определить количество молекул водяного пара (N), воспользуемся следующей формулой:
[N = nu {N_А}]
Здесь (N_А) – число Авогадро, равное 6,023·1023 1/моль.
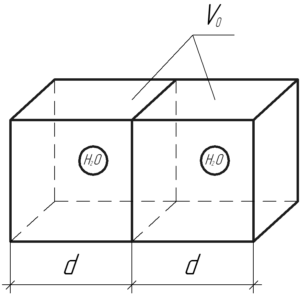
Тогда на каждую молекулу приходится куб объема (V_0), очевидно определяемый по формуле:
[{V_0} = frac{V}{N}]
[{V_0} = frac{{nu RT}}{{pnu {N_А}}} = frac{{RT}}{{p{N_А}}}]
Теперь посмотрите на схему к задаче. Каждая молекула условно находится в своем кубе, расстояние между двумя молекулами может меняться от 0 до (2d), где (d) – длина ребра куба. Среднее же расстояние (l) будет равно длине ребра куба (d):
[l = d]
Длину ребра (d) можно найти так:
[d = sqrt[3]{{{V_0}}}]
В итоге получим такую формулу:
[l = sqrt[3]{{frac{{RT}}{{p{N_А}}}}}]
Переведем температуру в шкалу Кельвина и посчитаем ответ:
[100^circ;C = 373;К]
[l = sqrt[3]{{frac{{8,31 cdot 373}}{{100 cdot {{10}^3} cdot 6,023 cdot {{10}^{23}}}}}} = 3,72 cdot {10^{ – 9}};м = 3,72;нм]
Ответ: 3,72 нм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.1.64 Какое количество вещества содержится в алюминиевой ложке массы 27 г? Относительная
4.1.66 Молекула двухатомного газа содержит 16 протонов и 16 нейтронов. Чем равна плотность
4.1.67 В сосуде вместимостью 4 м3 находится 4,8 кг идеального газа. Средняя квадратичная
Главная
страница
Система
уравнений газо-термодинамики
Средняя длина
свободного пробега
и среднее расстояние
между молекулами
Формула для средней длины свободного пробега
В одной из первых работ по кинетической
теории газов Максвеллом была получена формула
для средней длины λ свободного пробега:
λ = (2½ пσ) – 1, (1)
где
п –
числовая плотность (число молекул газа в единице объёма),
σ – эффективное
сечение соударения (ЭСС) молекул.
Как показывает анализ процесса столкновения
молекул, ЭСС является функцией от температуры газа Т и представляется формулой
σ(Т) = π rimp2
= π deq2
(1 + Т */Т), (2)
где
deq – равновесное расстояние между
молекулами;
Т* = 2/3 Ет/ k – глубина потенциальной ямы,
выраженная в температурных единицах;
Ет – глубина потенциальной ямы потенциала взаимодействия между молекулами,
выраженная в единицах энергии;
k – постоянная
Больцмана.
Если
обозначить через
le = 2¼ π½ deq (3)
эффективный линейный
размер молекулы, то с учётом (2) формула (1)
представляется в виде
λ = le– 2 п – 1
Θ, (4)
где
Θ = Т / (Т + Т
*).
Выражая числовую плотность п через удельный объём газа υ и
массу молекулы т
п = (т υ)–1,
(5)
можно формулу (4)
преобразовать к виду, в котором она будет использована в дальнейшем:
λ = β υ Θ,
где
β
= т
le– 2 = 2– ½ π–1 т deq– 2 –
постоянный для данного газа коэффициент.
Зависимость средней длины свободного пробега от температуры
Величина Θ принимает
значения, удовлетворяющие условиям:
0 < Θ < 1,
причём при Т
>> Т *
Θ ≈ 1,
а при Т
<< Т *
Θ ≈ Т / Т *.
(6)
Из соотношения (6) отнюдь не следует, что
длина свободного пробега λ стремится к нулю при Т → 0, т.к. удельный объём газа должен удовлетворять условию
υ ≥ υs(T),
где υs(T) – удельный объём насыщенного пара при температуре Т , причём
υs(T) → ∞ при Т
→ 0.
Отношение среднего расстояния между молекулами газа к средней длине
свободного пробега
Среднее
расстояние d
между центрами молекул выражается через числовую плотность п с помощью равенства
d = п–
1/3.
(7)
Исключив из (5) и (7) числовую плотность, получаем связь между
параметрами λ и d
λ / le = (d / le)3 Θ. (8)
Из (5) и (7)-(8) следует, что
d/λ = (le/d)2/Θ
= W,
где
W ≡
т1/3 ρ2/3/(βΘ).
Таблица 1. Оценочные значения параметров deq и β для некоторых газов
Вещество
О2 N2 4He Н2
Масса молекулы т, кг
5.35∙10–26
4.68∙10–26
6.69∙10–27
3.35∙10–27
Критическая плотность
ρс, кг/м3
436 313 69.64 30
Равновесное расстояние
между молекулами deq, м
3.8∙10–10
4.06∙10–10 3.5∙10–10 3.68∙10–10
Коэффициент β, кг/м2
8.3∙10–8
6.4∙10–8
1.22∙10–8
0.56∙10–8
Таблица 2 (составлена на основании данных о Стандартной
атмосфере).
Зависимость средней длины свободного пробега и среднего расстояния между
молекулами воздуха для земной атмосферы
_______________________________________________________________________
Высота над уровнем моря h, км 0 100 200 300
Числовая плотность п, м–3 2.55·1025 1.8·1019 5·1015 3·1014
Длина свободного пробега
λ, м 1·10–
7 1·10–1 300 3·103
Среднее расстояние между молекулами d, м
3·10–9 4·10–7 6·10–6 1·10–5
Отношение λ
/ d, безразмерн. 30 2.5·105 5·107 3·108
На
высоте h ≈ 250-500 км над
уровнем моря начинается самый верхний слой атмосферы – экзосфера, в котором длина свободного пробега столь
велика, что столкновениями между молекулами можно пренебречь. Движение молекул
в экзосфере полностью определяется дальнодействующими
силами, порождаемыми макрополями.
И.С. Житомирский
Дата последнего обновления: 30.05.09
Главная страница
Система
уравнений газо-термодинамики
Меню
- Главная
- Заказ решений
- Готовые решения
- Статьи
- Новости
- Авторы
Есть идеи?
Решения Чертовасайт решений Чертова А.Г. Воробьева А.А.
Поиск
Глава2. Молекулярная физика и термодинамика (§ 8-12) >> §8 Молекулярное строение вещества. Законы идеальных газов >> задача – 8.14
Условие:
Определить среднее расстояние между центрами молекул водяных паров при нормальных условиях и сравнить его с диаметром d самих молекул (d=0,311 нм).
При клике на картинку откроется ее увеличенная версия в новой вкладке.
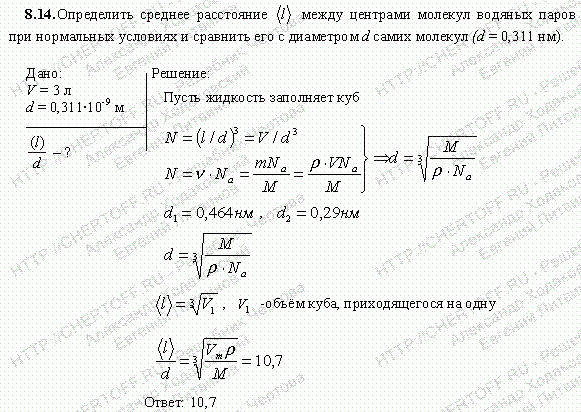
Не забываем поделиться записью!
Последние статьи
- Подходы к решению задач по физике
- Что такое физика и какие задачи и вопросы она решает?
- Общие рекомендации по решению статистических задач
- Он-лаин или офф-лаин обучение? Что выбрать?
- Изучение геометрии в восьмом классе без хлопот становится реальностью
Наши партнеры

© 2012 Решения Чертова | Авторы Bandit & AJ Акции | Sitemap | FAQ&ask
![]()
