Как найти среднее расстояние в физике

Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.

1. Половина пути

Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?

Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.

Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.

Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.

Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.

Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.

Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.

Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.

Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.

Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.

2. Средняя скорость по графику пути

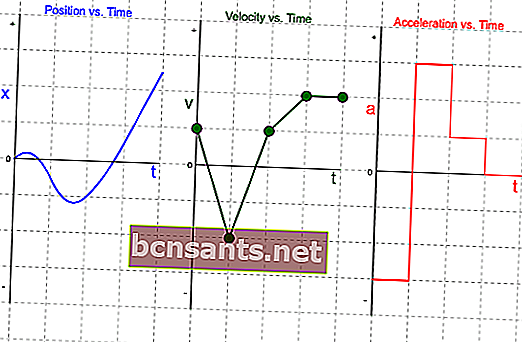
Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.

По графику видно, что движение состоит из четырех этапов:

1. Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
2. Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
3. Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
4. Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.

Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!

Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.

3. Средняя скорость по графику скорости

Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.

Читаем график. Движение состоит из трёх этапов

1. С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
2. От 2 до 6 с тело движется со скоростью 6 м/с
3. В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.

Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.

Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.

Общие рекомендации для решения задач на среднюю скорость

1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.

2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.

3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.

Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!

Физическая величина

Среднее расстояние между частицами (или среднее расстояние между частицами) является средним расстояние между микроскопическими частицами (обычно атомами или молекулами ) в макроскопическом теле.

Содержание

• 1 Неопределенность
• 2 Идеальный газ
  • 2.1 Распределение ближайших соседей
  • 2.2 Среднее расстояние и более высокие моменты распределения NN
• 3 Ссылки
• 4 См. Также

Неоднозначность

Из самых общих соображений, среднее расстояние между частицами пропорционально размеру объема, приходящегося на одну частицу 1 / n { displaystyle 1 / n}, т. Е.

⟨р⟩ ∼ 1 / n 1/3, { displaystyle langle r rangle sim 1 / n ^ {1/3},}

где n = N / V { displaystyle n = N / V}– плотность частиц. Однако, за исключением нескольких простых случаев, таких как модель идеального газа, точные вычисления коэффициента пропорциональности невозможны аналитически. Поэтому часто используются приближенные выражения. Одной из таких оценок является радиус Вигнера-Зейтца

(3 4 π n) 1/3, { displaystyle left ({ frac {3} {4 pi n}} right) ^ { 1/3},}

, который соответствует радиусу сферы, имеющей объем на частицу 1 / n { displaystyle 1 / n}. Другое популярное определение –

1 / n 1/3 { displaystyle 1 / n ^ {1/3}},

, соответствующее длине ребра куба с объемом на частицу 1 / п { displaystyle 1 / n}. Эти два определения различаются примерно в 1,61 { displaystyle 1.61}, поэтому нужно проявлять осторожность, если в статье не удается точно определить параметр. С другой стороны, он часто используется в качественных утверждениях, где такой числовой коэффициент либо не имеет значения, либо играет незначительную роль, например,

• «потенциальная энергия… пропорциональна некоторой степени n расстояния между частицами. r “(Теорема Вириала )
• « расстояние между частицами намного больше, чем тепловая длина волны де Бройля »(Кинетическая теория )

Идеальный газ

Распределение ближайших соседей

PDF расстояний NN в идеальном газе.

Мы хотим вычислить функцию распределения вероятностей расстояния до ближайшего соседа (NN) частицы. (Проблема была впервые рассмотрена; современный вывод см., например,.) Предположим, N { displaystyle N}частиц внутри сферы, имеющей объем V { displaystyle V}, так что n = N / V { displaystyle n = N / V}. Обратите внимание, что, поскольку частицы в идеальном газе не взаимодействуют, вероятность найти частицу на определенном расстоянии от другой частицы равна Сэм e как вероятность найти частицу на таком же расстоянии от любой другой точки; мы будем использовать центр сферы.

NN-частица на расстоянии r { displaystyle r}означает, что на ней находится ровно одна из N { displaystyle N}частиц расстояние, в то время как остальные N – 1 { displaystyle N-1}частицы находятся на больших расстояниях, т. е. где-то вне сферы с радиусом r { displaystyle r}.

Вероятность найти частицу на расстоянии от начала координат между r { displaystyle r}и r + dr { displaystyle r + dr}равна (4 π r 2 / V) dr { displaystyle (4 pi r ^ {2} / V) dr}, плюс мы имеем N { displaystyle N}виды способов выбрать, какую частицу, в то время как вероятность найти частицу за пределами этой сферы составляет 1–4 π r 3/3 V { displaystyle 1-4 pi r ^ {3} / 3V }. Искомое выражение тогда

PN (r) dr = 4 π r 2 dr NV (1 – 4 π 3 r 3 / V) N – 1 = 3 a (ra) 2 dr (1 – (ra) 3 1 N) N – 1 { displaystyle P_ {N} (r) dr = 4 pi r ^ {2} dr { frac {N} {V}} left (1 – { frac {4 pi } {3}} r ^ {3} / V right) ^ {N-1} = { frac {3} {a}} left ({ frac {r} {a}} right) ^ { 2} dr left (1- left ({ frac {r} {a}} right) ^ {3} { frac {1} {N}} right) ^ {N-1} ,}

где мы заменили

1 V = 3 4 π N a 3. { displaystyle { frac {1} {V}} = { frac {3} {4 pi Na ^ {3}}}.}

Обратите внимание, что a { displaystyle a}– радиус Вигнера-Зейтца. Наконец, взяв предел N → ∞ { displaystyle N rightarrow infty}и используя lim x → ∞ (1 + 1 x) x = e { displaystyle lim _ {x rightarrow infty} left (1 + { frac {1} {x}} right) ^ {x} = e}, получаем

P (r) = 3 а (ра) 2 е – (г / а) 3. { displaystyle P (r) = { frac {3} {a}} left ({ frac {r} {a}} right) ^ {2} e ^ {- (r / a) ^ {3 }} ,.}

Сразу проверяется, что

∫ 0 ∞ P (r) dr = 1. { displaystyle int _ {0} ^ { infty} P (r) dr = 1 ,.}

Пик распределения при

r peak = (2/3) 1/3 a ≈ 0,874 a. { displaystyle r _ { text {peak}} = left (2/3 right) ^ {1/3} a приблизительно 0.874a ,.}

Среднее расстояние и более высокие моменты распределения NN

⟨ rk⟩ знак равно ∫ 0 ∞ P (r) rkdr = 3 ak ∫ 0 ∞ xk + 2 e – x 3 dx, { displaystyle langle r ^ {k} rangle = int _ {0} ^ { infty} P (r) r ^ {k} dr = 3a ^ {k} int _ {0} ^ { infty} x ^ {k + 2} e ^ {- x ^ {3}} dx ,,}

или, используя замену t = x 3 { displaystyle t = x ^ {3}},

⟨rk⟩ = ak ∫ 0 ∞ tk / 3 e – tdt = АК Γ (1 + К 3), { Displaystyle langle r ^ {k} rangle = a ^ {k} int _ {0} ^ { infty} t ^ {k / 3} e ^ {- t } dt = a ^ {k} Gamma (1 + { frac {k} {3}}) ,,}

, где Γ { displaystyle Gamma}– это гамма-функция. Таким образом,

⟨r k⟩ = a k Γ (1 + k 3). { displaystyle langle r ^ {k} rangle = a ^ {k} Gamma (1 + { frac {k} {3}}) ,.}

В частности,

⟨r⟩ = a Γ (4 3) = a 3 Γ (1 3) ≈ 0,893 a. { displaystyle langle r rangle = a Gamma ({ frac {4} {3}}) = { frac {a} {3}} Gamma ({ frac {1} {3}}) приблизительно 0,893a ,.}

Ссылки

1. ^Герц, Пол (1909). “Über den gegenseitigen durchschnittlichen Abstand von Punkten, die mit bekannter mittlerer Dichte im Raume angeordnet sind”. Mathematische Annalen. 67 (3): 387–398. DOI : 10.1007 / BF01450410. ISSN 0025-5831.
2. ^Чандрасекхар, С. (1943-01-01). «Стохастические задачи физики и астрономии». Обзоры современной физики. 15 (1): 1–89. Бибкод : 1943RvMP… 15…. 1C. doi : 10.1103 / RevModPhys.15.1.

См. Также

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой – нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

• v – скорость объекта,
• S – расстояние, которое пройдено или должно быть пройдено объектом,
• t – время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S, n – количество этих участков, vср – средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср – средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn – отдельные неравномерные участки всего пути,
• t – общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S – общее пройденное расстояние,
• t1, t2, tn – время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N – механическая мощность,

F – сила,

v – скорость,

cos α – косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v – понятно что такое,

S – расстояние, которое требуется найти,

t – время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v – все та же скорость,

S – расстояние, пройденный путь,

t – время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
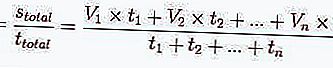