Загрузить PDF
Загрузить PDF
Ускорение характеризует быстроту изменения скорости как по величине, так и по направлению. Можно найти среднее ускорение, чтобы определить среднюю быстроту изменения скорости тела в течение определенного периода времени. Возможно, вы не знаете, как вычислить ускорение (так как это неповседневная задача), но с правильным подходом это не составит труда.
-

1
Определение ускорения. Ускорение — это быстрота увеличения или уменьшения скорости,[1]
или просто быстрота изменения скорости с течением времени.[2]
Ускорение — векторная величина, имеющая направление (включите его в ответ).- Обычно, если тело ускоряется при движении «вправо», «вверх» или «вперед», то ускорение имеет положительное (+) значение.
- Если тело ускоряется при движении «влево», «вниз» или «назад», то ускорение имеет отрицательное (+) значение.
-

2
Запишите определение ускорения в виде формулы. Как упоминалось выше, ускорение — это быстрота изменения скорости с течением времени.[3]
Есть два способа записать это определение в виде формулы:- aср = Δv/Δt (символ дельта «Δ» означает «изменение»).
- aср = (vк – vн)/(tк – tн), где vк — конечная скорость, vн — начальная скорость.
-

3
Найдите начальную и конечную скорости тела. Например, автомобиль, начинающий движение (вправо) со стоянки, имеет начальную скорость 0 м/с, а конечную скорость 500 м/с.[4]
- Движение вправо описывается положительными значениями, поэтому далее мы не будем указывать направление движения.
- Если автомобиль начинает движение вперед, а заканчивает его движением назад, конечная скорость имеет отрицательное значение.
-

4
Обратите внимание на изменение времени. Например, автомобилю может понадобиться 10 секунд, чтобы достичь конечной скорости. В этом случае tк = 10 с, а tн = 0 с.[5]
- Убедитесь, что скорость и время даются в соответствующих единицах измерения. Например, если скорость дана в км/ч, то время должно измеряться в часах.
-

5
Подставьте данные вам значения скорости и времени в формулу для вычисления среднего ускорения. В нашем примере:
- aср = (500 м/с – 0 м/с)/(10с – 0с)
- aср = (500 м/с)/(10с)
- aср = 50 м/с / с, то есть 50 м/с2.
-

6
Интерпретация результата. Среднее ускорение задает среднюю быстроту изменения скорости в течение определенного промежутка времени.[6]
В приведенном выше примере машина в среднем ускорялась на 50 м/с за каждую секунду. Запомните: параметры движения могут быть разными, но среднее ускорение будет таким же, только если изменение скорости и изменение времени не меняются:- Автомобиль может начать движение со скоростью 0 м/с и разогнаться за 10 секунд до 500 м/с.
- Автомобиль может начать движение со скоростью 0 м/с и разогнаться до 900 м/с, а затем сбросить скорость до 500 м/с за 10 секунд.
- Автомобиль может начать движение со скоростью 0 м/с, стоять на месте в течение 9 секунд, а затем за 1 секунду разогнаться до 500 м/с.
Реклама
-

1
Определение положительной и отрицательной скорости. Скорость имеет направление (так как это векторная величина), но указывать его, например, как «вверх» или «на север», весьма утомительно. Вместо этого в большинстве задач предполагается, что тело движется вдоль прямой линии. При движении в одном направлении скорость тела положительна, а при движении в противоположном направлении скорость тела отрицательна.[7]
- Например, синий поезд движется на восток со скоростью 500 м/с. Красный поезд движется на запад с такой же скоростью, но так как он движется в противоположном направлении, его скорость записывается так: -500 м/с.
-

2
Используйте определение ускорения, чтобы определить его знак (+ или -). Ускорение — быстрота изменения скорости с течением времени. Если вы не знаете, какой знак написать у значения ускорения, найдите изменение скорости:
- vконечная – vначальная = + или – ?
-

3
Ускорение в разных направлениях. Например, синий и красный поезда движутся в противоположных направлениях со скоростью 5 м/с. Представьте это движение на числовой прямой; синий поезд движется со скоростью 5 м/с в положительном направлении числовой прямой (то есть вправо), а красный поезд движется со скоростью -5 м/с в отрицательном направлении числовой прямой (то есть влево). Если каждый поезд увеличивает скорость на 2 м/с (в направлении его движения), то какой знак имеет ускорение?[8]
Давайте проверим:- Синий поезд движется в положительном направлении, поэтому его скорость с 5 м/с возрастает до 7 м/с. Конечная скорость равна 7 – 5 = +2. Поскольку изменение скорости положительно, то и ускорение положительно.
- Красный поезд движется в отрицательном направлении и увеличивает скорость с -5 м/с до -7 м/с. Конечная скорость равна -7 – (-5) = -7 + 5 = -2 м/с. Поскольку изменение скорости отрицательно, то и ускорение отрицательно.
-

4
Замедление.[9]
Например, самолет летит со скоростью 500 км/ч, а затем замедляется до 400 км/ч. Хотя самолет движется в положительном направлении, его ускорение отрицательно, так как он замедляется (то есть уменьшает скорость). Это можно проверить через вычисления: 400 – 500 = -100, то есть изменение скорости отрицательно, поэтому и ускорение отрицательно.[10]
- С другой стороны, если вертолет движется со скоростью -100 км/ч и разгоняется до -50 км/ч, то его ускорение положительно, потому что изменение скорости положительно: -50 – (-100) = 50 (хотя такого изменения скорости было недостаточно, чтобы изменить направление движения вертолета).
Реклама
Советы
Ускорение и скорость — векторные величины, которые задаются как значением, так и направлением. Величины, задающиеся только значением, называются скалярными (например, длина).[11]
Реклама
Об этой статье
Эту страницу просматривали 46 655 раз.
Была ли эта статья полезной?
Коллоквиум.
1. Механическое движение. Относительность
механического движения.
Механическое движение – это изменение
положения тела в пространстве относительно
других тел.
Относительность механического движения
Все тела во Вселенной движутся, поэтому
не существует тел, которые находятся в
абсолютном покое. По той же причине
определить движется тело или нет, можно
только относительно какого-либо другого
тела.
Например, автомобиль движется по дороге.
Дорога находится на планете Земля.
Дорога неподвижна. Поэтому можно измерить
скорость автомобиля относительно
неподвижной дороги. Но дорога неподвижна
относительно Земли. Однако сама Земля
вращается вокруг Солнца. Следовательно,
дорога вместе с автомобилем также
вращается вокруг Солнца. Следовательно,
автомобиль совершает не только
поступательное движение, но и вращательное
(относительно Солнца). А вот относительно
Земли автомобиль совершает только
поступательное движение. В этом
проявляется относительность механического
движения.
Относительность механического движения
– это зависимость траектории движения
тела, пройденного пути, перемещения и
скорости от выбора системы отсчёта.
2. Перемещение и скорость.
Перемещение
– это вектор, соединяющий начальное и
конечное положение точки. Направление
и величина перемещения определяются
отрезком прямой между начальной и
конечной точками движения.
Скорость.
Механическое
движение характеризуется еще и тем,
насколько быстро движется точка (тело).
Эта характеристика называется скорость
движения.
Скорость – величина векторная. Для того,
чтобы полностью задать ее, надо задать
собственно величину скорости и
направление, вдоль которого она измерена.
Обычно рассматривается скорость тела
вдоль траектории его движения. Тогда
величина скорости определяется как
путь, пройденный в единицу времени.
Иначе говоря, для того, чтобы найти
скорость вдоль траектории движения
надо путь разделить на время, за которое
он был пройден.
Формулы
для решения:
Пусть
v
–
скорость, s
–
путь, t
– время. Скорость
измеряется вдоль траектории движения.
Тогда:

Перемещение
определяется как геометрическая сумма
отрезков пути. Для простейшего случая,
когда один участок пути направлен
перпендикулярно другому решается
прямоугольный треугольник:
![]()
3. Виды движения. Ускорение.
В современной механике движение тела
подразделяется на виды, и существует
следующая классификация видов движения
тела:
1. Поступательное движение,
при котором любая прямая линия, связанная
с телом, остается при движении параллельной
самой себе.
2. Вращательное движение
или вращение тела вокруг своей оси,
считающейся неподвижной.
3. Сложное
движение тела, состоящее из
поступательного и вращательного
движений.
Ускорение – это величина,
которая характеризует быстроту изменения
скорости.
Среднее ускорение
Среднее
ускорение> – это отношение
изменения скорости к промежутку времени,
за который это изменении произошло.
Определить среднее ускорение можно
формулой:
![]()
где
![]() –
–
вектор ускорения.
Направление
вектора ускорения совпадает с направлением
изменения скорости Δ![]()
=
![]() –
–
![]() 0
0
(здесь
![]() 0
0
– это начальная скорость, то есть
скорость, с которой тело начало
ускоряться).
В
момент времени t1 (см. рис 1.8) тело имеет
скорость
![]() 0.
0.
В момент времени t2 тело имеет скорость
![]() .
.
Согласно правилу вычитания векторов
найдём вектор изменения скорости Δ![]()
=
![]() –
–
![]() 0.
0.
Тогда определить ускорение можно так:


Рис.
1.8. Среднее ускорение.
В
СИ единица ускорения – это 1
метр в секунду за секунду (или метр на
секунду в квадрате), то есть

Метр
на секунду в квадрате равен ускорению
прямолинейно движущейся точки, при
котором за одну секунду скорость этой
точки увеличивается на 1 м/с. Иными
словами, ускорение определяет, насколько
изменяется скорость тела за одну секунду.
Например, если ускорение равно 5 м/с2,
то это означает, что скорость тела каждую
секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное
ускорение тела (материальной точки)
в данный момент времени – это физическая
величина, равная пределу, к которому
стремится среднее ускорение при
стремлении промежутка времени к нулю.
Иными словами – это ускорение, которое
развивает тело за очень короткий отрезок
времени:
![]()
Направление
ускорения также совпадает с направлением
изменения скорости Δ![]()
при очень малых значениях промежутка
времени, за который происходит изменение
скорости. Вектор ускорения может быть
задан проекциями на соответствующие
оси координат в данной системе отсчёта
(проекциями аХ, aY, aZ).
При
ускоренном прямолинейном движении
скорость тела возрастает по модулю, то
есть
v2
> v1
а направление вектора ускорения совпадает
с вектором скорости
![]() 2.
2.
Если
скорость тела по модулю уменьшается,
то есть
v2
< v1
то направление вектора ускорения
противоположно направлению вектора
скорости
![]() 2.
2.
Иначе говоря, в данном случае происходит
замедление движения, при этом
ускорение будет отрицательным (а < 0).
На рис. 1.9 показано направление векторов
ускорения при прямолинейном движении
тела для случая ускорения и замедления.
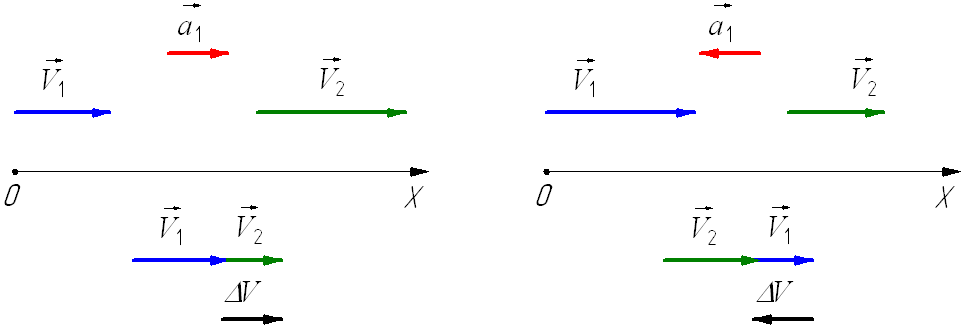
Рис.
1.9. Мгновенное ускорение.
При
движении по криволинейной траектории
изменяется не только модуль скорости,
но и её направление. В этом случае вектор
ускорение представляют в виде двух
составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное
(касательное) ускорение – это
составляющая вектора ускорения,
направленная вдоль касательной к
траектории в данной точке траектории
движения. Тангенциальное ускорение
характеризует изменение скорости по
модулю при криволинейном движении.

Рис.
1.10. Тангенциальное ускорение.
Направление
вектора тангенциального ускорения
![]() τ
τ
(см. рис. 1.10) совпадает с направлением
линейной скорости или противоположно
ему. То есть вектор тангенциального
ускорения лежит на одной оси с касательной
окружности, которая является траекторией
движения тела.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В физике рассмотрением особенностей движения макроскопических твердых тел занимается кинематика. Этот раздел механики оперирует такими понятиями, как скорость, ускорение и путь. В данной статье мы сосредоточим свое внимание на вопросах, что такое мгновенное ускорение и скорость. Также рассмотрим, какими формулами можно определить эти величины.
Нахождение скорости
Об этом понятии известно каждому школьнику, начиная уже с младших классов. Все ученики знакомы с приведенной ниже формулой:
 Вам будет интересно:Геохимический барьер: определение термина, особенности
Вам будет интересно:Геохимический барьер: определение термина, особенности
v = S/t.
Здесь S – путь, который преодолело движущееся тело за время t. Данное выражение позволяет рассчитать некоторую среднюю скорость v. Действительно, нам ведь неизвестно, каким образом двигалось тело, на каком участке пути оно перемещалось быстрее, а на каком медленнее. Даже не исключена ситуация, что в некоторой точке пути оно находилось в состоянии покоя какое-то время. Единственное, что известно, это пройденный путь и соответствующий ему временной отрезок.
В старших классах школ скорость, как физическая величина, рассматривается в новом свете. Ученикам предлагают следующее ее определение:
v = dS/dt.
Чтобы понять это выражение, нужно знать, как вычисляется производная от некоторой функции. В данном случае – это S(t). Поскольку производная характеризует поведение кривой в данной конкретной точке, то вычисляемая по формуле выше скорость называется мгновенной.
Ускорение

Если механическое движение является переменным, то для его точного описания необходимо знать не только скорость, но и величину, которая показывает, как она изменяется во времени. Это – ускорение, которое является производная по времени скорости. А та, в свою очередь, есть производная по времени пути. Формула мгновенного ускорения имеет вид:
a = dv/dt.
Благодаря этому равенству можно определить изменение величины v в любой точке траектории.
По аналогии со скоростью, среднее ускорение вычисляется по такой формуле:
a = Δv/Δt.
Здесь Δv – это изменение модуля скорости тела за промежуток времени Δt. Очевидно, что в течение этого периода тело способно как ускоряться, так и замедляться. Величина a, определенная из выражения выше, покажет лишь в среднем быстроту изменения скорости.
Движение с постоянным ускорением
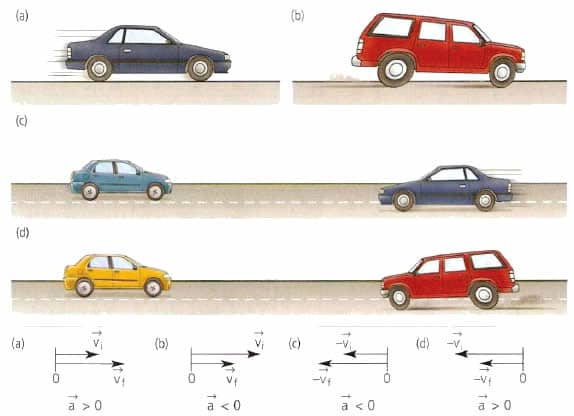
Отличительной особенностью этого типа перемещения тел в пространстве является постоянство величины а, то есть a=const.
Это движение также называют равноускоренным или равнозамедленным в зависимости от взаимного направления векторов скорости и ускорения. Ниже такое перемещение рассмотрим на примере двух наиболее распространенных траекторий: прямой линии и окружности.
При перемещении по прямой линии во время равноускоренного движения мгновенная скорость и ускорение, а также величина пройденного пути, связаны следующими равенствами:
v = v0 ± a*t;
S = v0*t ± a*t2/2.
Здесь v0 – это значение скорости, которым тело обладало до появления ускорения a. Заметим один нюанс. Для данного типа перемещения бессмысленно говорить о мгновенном ускорении, поскольку в любой точке траектории оно будет одним и тем же. Иными словами, мгновенная и средняя величины его будут равны друг другу.
Что касается скорости, то первое выражение позволяет определить ее в любой момент времени. То есть это будет мгновенный показатель. Для расчета средней скорости необходимо воспользоваться представленным выше выражением, то есть:
v = S/t = v0 ± a*(t1 + t2)/2.
Здесь t1 и t2 – это моменты времени, между которыми вычисляют среднюю скорость.
Знак “плюс” во всех формулах соответствует ускоренному передвижению. Соответственно знак “минус” – замедленному.
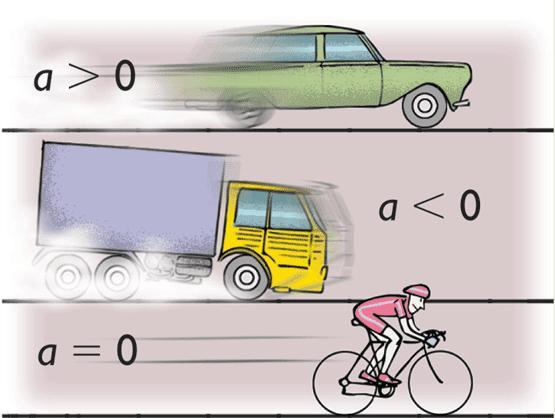
При изучении движения по окружности с постоянным ускорением в физике используют угловые характеристики, которые аналогичны соответствующим линейным. К ним относится угол поворота θ, угловая скорость и ускорение (ω и α). Эти величины связаны в равенства, аналогичные выражениям равноускоренного движения по прямой линии, которые приводятся ниже:
ω = ω0 ± α*t;
θ = ω0*t ± α*t2/2.
При этом угловые характеристики связаны с линейными следующим образом:
S = θ*R;
v = ω*R;
a = α*R.
Здесь R – радиус окружности.
Задача на определение среднего и мгновенного ускорения
Известно, что тело движется по сложной траектории. Его мгновенная скорость меняется по времени следующим образом:
v = 10 – 3*t + t3.
Чему равно мгновенное ускорение тела в момент t=3 (секунды)? Найти среднее ускорение за промежуток времени от двух до четырех секунд.
На первый вопрос задачи ответить несложно, если вычислить производную от функции v(t). Получаем:
a = |dv/dt|t=2;
а = |3*t2 – 3|t=2 = 24 м/с2.
Для определения среднего ускорения, следует воспользоваться таким выражением:
a = (v2 – v1)/(t2 – t1);
а = ((10 – 3*4 + 43) – (10 – 3*2 + 23))/2 = 25 м/c2.
Из расчетов следует, что среднее ускорение немного превышает мгновенное в середине рассмотренного временного промежутка.
Ускорение тела в физике, теория и онлайн калькуляторы
Ускорение тела
Определение
Ускорением тела называют векторную величину показывающую быстроту изменения скорости движения тела. Обозначают ускорение как $overline{a}$.
Среднее ускорение тела
Допустим, что в моменты времени $t$ и $t+Delta t$ скорости равны $overline{v}(t)$ и $overline{v}(t+Delta t)$. Получается, что за время $Delta t$ скорость изменяется на величину:
[Delta overline{v}=overline{v}left(t+Delta tright)-overline{v}left(tright)left(1right),]
тогда среднее ускорение тела равно:
[leftlangle overline{a}rightrangle left(t, t+Delta tright)=frac{Delta overline{v}}{Delta t}left(2right).]
Мгновенное ускорение тела
Устремим промежуток времени $Delta t$ к нулю, тогда из уравнения (2) получим:
[overline{a}={mathop{lim }_{Delta tto 0} frac{Delta overline{v}}{Delta t}=frac{doverline{v}}{dt}left(3right). }]
Формула (3) является определением мгновенного ускорения. Принимая во внимание, что в декартовой системе координат:
[overline{r}=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(4right), а overline{v}=frac{doverline{r}}{dt}(5)]
получаем:
[overline{a}=overline{i}frac{d^2x}{dt^2}+overline{j}frac{d^2y}{dt^2}+overline{k}frac{d^2z}{dt^2}=frac{d^2overline{r}}{dt^2}left(6right).]
Из выражения (6) следует, что проекции ускорения на оси координат (X,Y,Z) равны:
[left{ begin{array}{c}
a_x=frac{d^2x}{dt^2}, \
a_y=frac{d^2y}{dt^2} \
a_z=frac{d^2z}{dt^2}. end{array}
right.(7),]
При этом модуль ускорения найдем в соответствии с выражением:
[a=sqrt{a^2_x+a^2_y{+a}^2_z}.]
Для выяснения вопроса о направлении ускорения движения тела Вектор скорости представим как:
[overline{v}=voverline{tau }left(8right),]
где $v$ – модуль скорости тела; $overline{tau }$ – единичный вектор касательный к траектории движения материальной точки. Подставим выражение (8) в определение мгновенной скорости, получим:
[overline{a}={frac{doverline{v}}{dt} =frac{d}{dt}left(voverline{tau }right)=overline{tau }frac{dv}{dt}+vfrac{doverline{tau }}{dt}left(9right). }]
Единичный касательный вектор $overline{tau }$ определяется точкой траектории, которая в свою очередь характеризуется расстоянием ($s$) от начальной точки. Значит вектор $overline{tau }$ – это функция от $s$:
[overline{tau }=overline{tau }left(sright)left(10right).]
Параметр $s$ – функция от времени. Получаем:
[frac{doverline{tau }}{dt}=frac{doverline{tau }}{ds}frac{ds}{dt}left(11right),]
где вектор $overline{tau }$ по модулю не изменяется. Это означает, что вектор $frac{doverline{tau }}{ds}$ перпендикулярен $overline{tau }$. Вектор $overline{tau }{rm }$ является касательным к траектории, $frac{doverline{tau }}{ds}$ перпендикулярен к этой касательной, то есть, направлен по нормали, которая называется главной. Единичный вектор в направлении главной нормали обозначим $overline{n}$.
Величина $left|frac{doverline{tau }}{ds}right|=frac{1}{R}$, где $R$ – радиус кривизны траектории.
И так мы получили:
[frac{doverline{tau }}{ds}=frac{overline{n}}{R}left(12right).]
Принимая во внимание, что $frac{ds}{dt}=v$, из (9) можно записать следующее:
[overline{a}=overline{tau }frac{dv}{dt}+vfrac{overline{n}}{R}v=overline{tau }frac{dv}{dt}+frac{v^2}{R}overline{n}left(13right).]
Выражение (13) показывает, что полное ускорение тела состоит из двух компонент, которые взаимно перпендикулярны. Тангенциального ускорения (${overline{a}}_{tau }$), направленного по касательной к траектории движения и равного:
[{overline{a}}_{tau }=overline{tau }frac{dv}{dt}(14)]
и нормального (центростремительного) ускорения (${overline{a}}_n$), направленного перпендикулярно касательной к траектории в точке расположения тела по главной нормали (к центру кривизны траектории) и равного:
[{overline{a}}_n=frac{v^2}{R}overline{n}left(15right).]
Модуль полного ускорения равен:
[a=sqrt{{left(frac{v^2}{R}right)}^2+{left(frac{dv}{dt}right)}^2}left(16right).]
Единицей измерения ускорения в Международной системе единиц (СИ) является метр на секунду в квадрате:
[left[aright]=frac{м}{с^2}.]
Прямолинейное движение тела
Если траекторией движения материальной точки является прямая, то вектор ускорения направлен вдоль той же прямой, что и вектор скорости. Изменяется только величина скорости.
Переменное движение называют ускоренным, если скорость материальной точки постоянно увеличивается по модулю. При этом $a>0$, векторы ускорения и скорости сонаправлены.
Если скорость по модулю убывает, то движение называют замедленным ($a<0;; overline{a}uparrow downarrow overline{v}$).
Движение материальной точки называют равнопеременным и прямолинейным, если движение происходит с постоянным ускорением ($overline{a}=const$). При равнопеременном движении мгновенная скорость ($overline{v}$) и ускорение материальной точки связаны выражением:
[overline{v}={overline{v}}_0+overline{a}t left(3right),]
где ${overline{v}}_0$ – скорость тела в начальный момент времени.
Примеры задач с решением
Пример 1
Задание: Движения двух материальных точек заданы следующими кинематическими уравнениями: $x_1=A+Bt-Ct^2$ и $x_2=D+Et+Ft^2,$ чему равны ускорения этих двух точек в момент времени, когда равны их скорости, если $A$, B,C,D,E.F – постоянные большие нуля.
Решение: Найдем ускорение первой материальной точки:
[{a_1=a}_{x1}=frac{d^2x_1}{dt^2}=frac{d^2}{dt^2}left(A+Bt-Ct^2right)=-2С (frac{м}{с^2}).]
У второй материальной точки ускорение будет равно:
[{a_2=a}_{x2}=frac{d^2x_2}{dt^2}=frac{d^2}{dt^2}left(D+Et+Ft^2right)=2Fleft(frac{м}{с^2}right).]
Мы получили, что точки движутся с постоянными ускорениями, которые не зависят от времени, поэтому момент времени, в который скорости равны, искать не обязательно.
Ответ: $a_1=-2Сfrac{м}{с^2}$, $a_2=2Ffrac{м}{с^2}$
Пример 2
Задание: Движение материальной точки задано уравнением: $overline{r}left(tright)=Aleft(overline{i}{cos left(omega tright)+overline{j}{sin left(omega tright) } }right),$ где $A$ и $omega $ – постоянные величины. Начертите траекторию движения точки, изобразите на ней вектор ускорения этой точки. Каков модуль центростремительного ускорения ($a_n$) точки в этом случае?
Решение: Рассмотрим уравнение движения нашей точки:
[overline{r}left(tright)=Aleft(overline{i}{cos left(omega tright)+overline{j}{sin left(omega tright) } }right) left(2.1right).]
В координатной записи уравнению (2.1) соответствует система уравнений:
[left{ begin{array}{c}
xleft(tright)=A{rm cos}left(omega tright), \
y(t)=A{sin left(omega tright) } end{array}
left(2.2right).right.]
Возведем в квадрат каждое уравнение системы (2.2) и сложим их:
[x^2+y^2=A^2left(2.3right).]
Мы получили уравнение окружности радиуса $A$ (рис.1).
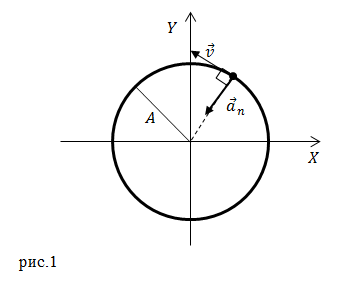
Величину центростремительного ускорения, учитывая, что радиус траектории равен А, найдем как:
[a_n=frac{v^2}{R}=frac{v^2}{A}left(2.4right).]
Проекции скорости на оси координат равны:
[left{ begin{array}{c}
v_x=frac{dxleft(tright)}{dt}=-A omega {rm sin}left(omega tright), \
v_y=frac{dyleft(tright)}{dt}=A{omega cos left(omega tright) } end{array}
left(2.5right).right.]
Величина скорости равна:
[v=sqrt{v^2_x+v^2_y}=Aomega left(2.6right).]
Подставим результат (2.6) в (2.4), нормальное ускорение равно:
[a_n=frac{A^2{omega }^2}{A}=A{omega }^2.]
Легко показать, что движение точки в нашем случае является равномерным движением по окружности и полное ускорение точки равно центростремительному ускорению. Для этого можно взять производную от проекций скоростей (2.5) по времени и используя выражение:
[a=sqrt{a^2_x+a^2_y}left(2.7right)]
получить:
[a=A{omega }^2.]
Ответ: $a_n=A{omega }^2$
Читать дальше: условие равновесия тела.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Ускорение характеризует быстроту изменения скорости как по величине, так и по направлению. Можно найти среднее ускорение, чтобы определить среднюю быстроту изменения скорости тела в течение определенного периода времени. Вы можете быть незнакомы с вычислением ускорения (та как это не повседневные задачи), но эта статья расскажет вам, как быстро найти среднее ускорение.
Метод 1 из 2: Вычисление среднего ускорения
-

Определение ускорение. Ускорение – это быстрота увеличения или уменьшения скорости, или просто быстрота изменения скорости с течением времени. Ускорение – векторная величина, имеющая направление (включите его в ответ).
- Обычно, если тело ускоряется при движении «вправо», «вверх» или «вперед», то ускорение имеет положительное (+) значение.
- Если тело ускоряется при движении «влево», «вниз» или «назад», то ускорение имеет отрицательное (+) значение.
-

Запишите определение ускорения в виде формулы. Как упоминалось выше, ускорение – это быстрота изменения скорости с течением времени. Есть два способа записать это определение в виде формулы:
- aср = /Δt (Символ дельта «Δ» означает «изменение»).
- aср = /(tк – tн), где vк – конечная скорость, vн – начальная скорость.
-

Найдите начальную и конечную скорости тела. Например, автомобиль, начинающий движение (вправо) со стоянки, имеет начальную скорость 0 м/с, а конечную скорость 500 м/с .
- Движение вправо описывается положительными значениями, поэтому далее мы не будем указывать направление движения.
- Если автомобиль начинает движение вперед, а заканчивает его движением назад, конечная скорость имеет отрицательное значение.
-

Обратите внимание на изменение времени. Например, автомобилю может понадобиться 10 секунд, чтобы достичь конечной скорости. В этом случае tк = 10 с, а tн = 0 с.
- Убедитесь, что скорость и время даются в соответствующих единицах измерения. Например, если скорость дана в км/ч, то время должно измеряться в часах.
-

Подставьте данные вам значения скорости и времени в формулу для вычисления среднего ускорения. В нашем примере:
- aср = /(10с – 0с)
- aср = /(10с)
- aср = 50 м/с / с, то есть 50 м/с.
-

Интерпретация результата. Среднее ускорение задает среднюю быстроту изменения скорости в течение определенного промежутка времени. В приведенном выше примере машина в среднем ускорялась на 50 м/с за каждую секунду. Запомните: параметры движения могут быть разными, но среднее ускорение будет таким же, только если изменение скорости и изменение времени не меняются:
- Автомобиль может начать движение со скоростью 0 м/с и разогнаться за 10 секунд до 500 м/с.
- Автомобиль может начать движение со скоростью 0 м/с и разогнаться до 900 м/с, а затем сбросить скорость до 500 м/с за 10 секунд.
- Автомобиль может начать движение со скоростью 0 м/с, стоять на месте в течение 9 секунд, а затем за 1 секунду разогнаться до 500 м/с.
Метод 2 из 2: Положительное и отрицательное ускорение
-

Определение положительной и отрицательной скорости. Скорость имеет направление (так как это векторная величина), но указывать его, например, как «вверх» или «на север», весьма утомительно. Вместо этого в большинстве задач предполагается, что тело движется вдоль прямой линии. При движении в одном направлении скорость тела положительна, а при движении в противоположном направлении скорость тела отрицательна.
- Например, синий поезд движется на восток со скоростью 500 м/с. Красный поезд движется на запад с такой же скоростью, но так как он движется в противоположном направлении, его скорость записывается так: -500 м/с.
-

Используйте определение ускорения, чтобы определить его знак (+ или -). Ускорение – быстрота изменения скорости с течением времени. Если вы не знаете, какой знак написать у значения ускорения, найдите изменение скорости:
- vконечная – vначальная = + или – ?
-

Ускорение в разных направлениях. Например, синий поезд и красный поезда движутся в противоположных направлениях со скоростью 5 м/с. Представьте это движение на числовой прямой; синий поезд движется со скоростью 5 м/с в положительном направлении числовой прямой (то есть вправо), а красный поезд движется со скоростью -5 м/с в отрицательном направлении числовой прямой (то есть влево). Если каждый поезд увеличивает скорость на 2 м/с (в направлении его движения), то какой знак имеет ускорение? Давайте проверим:
- Синий поезд движется в положительном направлении, поэтому его скорость с 5 м/с возрастает до 7 м/с. Конечная скорость равна 7 – 5 = +2. Поскольку изменение скорости положительно, то и ускорение положительно.
- Красный поезд движется в отрицательном направлении и увеличивает скорость с -5 м/с до -7 м/с. Конечная скорость равна -7 – (-5) = -7 + 5 = -2 м/с. Поскольку изменение скорости отрицательно, то и ускорение отрицательно.
-

Замедление. Например, самолет летит со скоростью 500 км/ч, а затем замедляется до 400 км/ч. Хотя самолет движется в положительном направлении, его ускорение отрицательно, так как он замедляется (то есть уменьшает скорость). Это можно проверить через вычисления: 400 – 500 = -100, то есть изменение скорости отрицательно, поэтому и ускорение отрицательно.
- С другой стороны, если вертолет движется со скоростью -100 км/ч и разгоняется до -50 км/ч, то его ускорение положительно, потому что изменение скорости положительно: -50 – (-100) = 50 (хотя такого изменения скорости было недостаточно, чтобы изменить направление движения вертолета).
Советы
Ускорение и скорость – векторные величины, которые задаются как значением, так и направлением. Величины, задающиеся только значением, называются скалярными (например, длина).
