Среднее арифметическое, размах, мода и медиана
- Алгебра
- Среднее арифметическое, размах, мода и медиана
Статистические характеристики
количество чисел
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда
чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите
рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих
чисел на число слагаемых.
Для ряда a1,a1,..,an среднее арифметическое вычисляется по
формуле:
begin{align}
& overline{a}=frac{a_1+a_2+…+a_n}{n}\
end{align}
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
begin{align}
& overline{a}=frac{5,24+6,97+8,56+7,32+6,23}{5}=6.864\
end{align}
Размахом ряда чисел называется разность между наибольшим и наименьшим из
этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще
других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется
число, записанное посередине, а медианой упорядоченного ряда чисел с чётным
числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного
ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды
ряда.
-
Среднее арифметическое чисел 30, 5, 23, 5, 28, 30
begin{align}
& overline{a}=frac{30+5+23+5+28+30}{6}=20frac{1}{6}\
end{align}Размах ряда: 30-5=25
Моды ряда: 5 и 30
Медиана ряда: 25.5
-
Среднее арифметическое чисел 40, 35, 30, 25, 30, 35
begin{align}
& overline{a}=frac{40+35+30+25+30+35}{6}=32frac{1}{2}\
end{align}Размах ряда: 40-25=15
Моды ряда: 30, 35
Медиана ряда: 32.5
-
Среднее арифметическое чисел 21, 18,5, 25,3, 18,5, 17,9
begin{align}
& overline{a}=frac{21+18,5+25,3+18,5+17,9}{5}=20,24\
end{align}Размах ряда: 25,3-17,9=7,4
Мода ряда: 18,5
Медиана ряда: 18,5
Примеры
Примеры нахождения среднего арифметического отрицательных и вещественных чисел.
-
Среднее арифметическое чисел 67,1, 68,2, 67,1, 70,4, 68,2
begin{align}
& overline{a}=frac{67,1+68,2+67,1+70,4+68,2}{5}=68,2\
end{align}Размах ряда: 70,4-67,1=3,3
Моды ряда: 67.1, 68.2
Медиана ряда: 68.2
-
Среднее арифметическое чисел 0,6, 0,8, 0,5, 0,9, 1,1
begin{align}
& overline{a}=frac{0,6+0,8+0,5+0,9+1,1}{5}=0.78\
end{align}Размах ряда: 1,1-0,5=0.6
Ряд не имеет моды
Медиана ряда: 0.8
-
Среднее арифметическое чисел -21, -33, -35, -19, -20, -22
begin{align}
& overline{a}=frac{(-21)+(-33)+(-35)+(-19)+(-20)+(-22)}{6}=-25\
end{align}Размах ряда: (-19)-(-35)=16
Ряд не имеет моды
Медиана ряда: -21,5
-
Среднее арифметическое чисел -4, -6, 0, -4, 0, 6, 8, -12
begin{align}
& overline{a}=frac{(-4)+(-6)+0+(-4)+0+6+8+(-12)}{8}=-1,5\
end{align}Размах ряда: 8-(-12)=20
Моды ряда: -4, 0
Медиана ряда: -2
-
Среднее арифметическое чисел 275, 286, 250, 290, 296, 315, 325
begin{align}
& overline{a}=frac{275+286+250+290+296+315+325}{7}=291\
end{align}Размах ряда: 325-250=75
Ряд не имеет моды
Медиана ряда: 290
-
Среднее арифметическое чисел 38, 42, 36, 45, 48, 45, 45, 42, 40, 47, 39
begin{align}
& overline{a}=frac{38+42+36+45+48+45+45+42+40+47+39}{11}=42frac{6}{11}\
end{align}Размах ряда: 48-36=12
Мода ряда: 45
Медиана ряда: 42
-
Среднее арифметическое чисел 3,8, 7,2, 6,4, 6,8, 7,2
begin{align}
& overline{a}=frac{3,8+7,2+6,4+6,8+7,2}{5}=6,28\
end{align}Размах ряда: 7,2-3,8=3,4
Мода ряда: 7,2
Медиана ряда: 6,8
-
Среднее арифметическое чисел 21,6, 37,3, 16,4, 12,6
begin{align}
& overline{a}=frac{21,6+37,3+16,4+12,6}{4}=21,025\
end{align}Размах ряда: 37,3-12,6=24,7
Мода ряда: 12,6
Медиана ряда: 17,1
| Тип: | изучение нового материала. |
| Цели: | Образовательные: ввести понятие числового набора и средних значений – среднего арифметического, медианы, моды числового набора; научить находить средние и выбирать из них наиболее подходящие для описания числового набора. Развивающие: развивать логическое Воспитательные: развивать внимание, |
Ход урока
I. Оргмомент. Тема, цели, план урока.
II. Повторение.
Понятие среднего арифметического двух чисел,
координаты середины отрезка на числовой прямой,
представление о равноплечных рычажных весах.
III. Изучение нового материала.
1) Понятие о числовом наборе как наборе числовых
данных, полученных в результате измерений или
сбора информации. Примеры таблиц с результатами
измерений или статистических данных.
Упорядоченные числовые наборы.
2) Понятие о средних величинах как величинах,
характеризующих числовой набор в целом
(характеристики положения).
3) Среднее арифметическое нескольких чисел.
![]()
Интерпретация среднего арифметического как
центра масс.
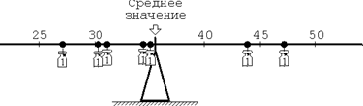
Закрепление.
Задача 1. Ученик получил в течение
учебной четверти оценки 5, 2, 4, 5, 5, 4, 4, 5, 5, 5.
Вычислите его средний балл.
Задача 2. В магазин привезли конфеты,
расфасованные в различные пакеты. Оказалось, что
привезли 20 пакетов по 200 г, 10 пакетов по 500 г и 5
пакетов по 1 кг. Каков средний вес пакета?
Задача 3. Наблюдения на станции метро в
течение недели показали, что в среднем за день в
метро входит 5 тыс. чел. Сколько человек вошло в
метро за неделю?
При обсуждении решения задачи 3 подчеркнуть,
что по значению среднего арифметического
однозначно восстанавливается сумма чисел
набора.
4) Медиана числового набора. Определение для
наборов с четным и нечетным количеством чисел.
Устойчивость медианы по отношению к выбросам.
Пример, когда медиана лучше характеризует набор,
чем среднее арифметическое (численность
населения городов-миллионников в тыс. чел.).
| Город | Год | ||
| 1979 | 1989 | 2002 | |
| Волгоград | 926 | 999 | 1013 |
| Екатеринбург | 1210 | 1296 | 1293 |
| Казань | 989 | 1085 | 1105 |
| Москва | 8057 | 8878 | 10358 |
| Нижний Новгород | 1342 | 1400 | 1311 |
| Новосибирск | 1309 | 1420 | 1426 |
| Омск | 1016 | 1149 | 1134 |
| Пермь | 989 | 1041 | 1000 |
| Ростов-на-Дону | 925 | 1008 | 1070 |
| Самара | 1192 | 1222 | 1158 |
| Санкт-Петербург | 4569 | 4989 | 4669 |
| Уфа | 977 | 1080 | 1042 |
| Челябинск | 1030 | 1107 | 1078 |
Закрепление.
Задача 4. Отметьте числа и их медианы
на числовой оси:
а) 8, 11, 3; б) 7, 4, 8, 1, 5; в) 10, 3, 9, 8, 4, 5, 7.
Задача 5. Вычислите медиану и среднее
арифметическое чисел:
а) 1, 3, 5, 7, 9; б) 1, 3, 5, 7, 14; в) 1, 3, 5, 7, 9, 11; г) 1, 3, 5, 7, 9, 16.
Сравните медиану и среднее значение.
5) Мода числового набора. Примеры наборов:
унимодальный, бимодальный, полимодальный, без
моды. Примеры наборов нечисловой природы, для
которых определено понятие моды (результаты
выборов, покупаемые размеры одежды и т.п.).
Закрепление.
Задача 6. Найдите моду числового
набора из задачи 1.
6) Свойства средних на примере среднего
арифметического.
Задача 7. Вычислите среднее
арифметическое наборов чисел:
а) 1, 2, 3, 4, 5; б) 3, 4, 5, 6, 7; в) 10, 11, 12, 13, 14.
Какую закономерность в поведении среднего
значения можно заметить?
Задача 8. Вычислите среднее
арифметическое наборов чисел:
а) 2, 4, 7, 8, 9; б) 20, 40, 70, 80, 90; в) 200, 400, 700, 800, 900.
Какую закономерность в поведении среднего
значения можно заметить?
IV. Домашнее задание.
1) В таблице 14 [1, п.6] приведены четвертные оценки
учащихся класса по математике, русскому и
иностранному языкам. Составьте для каждого
предмета таблицу подсчета числа учеников,
имеющих оценки 5, 4, 3. С помощью этой таблицы
найдите средний балл, медиану и моду оценок по
предметам. Какая характеристика точнее отражает
успеваемость класса?
2) Найдите медиану для числовых наборов из задач
7 и 8. Опишите закономерности поведения медианы в
каждом из этих случаев.
3) Сформулируйте, как изменяется мода: а) при
умножении каждого числа набора на одно и то же
число, б) при изменении каждого числа набора на
одно и то же число. Приведите примеры.
V. Итог урока.
- Что такое средние значения?
- Какие виды средних вы знаете?
- Какими преимуществами обладает каждый из
изученных видов средних?
Литература.
1. Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко
И.В. Теория вероятностей и статистика. – М.: МЦНМО:
ОАО “Московские учебники”, 2008. – 256 с.
Среднее арифметическое, мода и медиана
- Предмет, цели и методы математической статистики
- Метод выборочных исследований
- Средняя арифметическая, простая и взвешенная
- Мода и медиана
- Примеры
Предмет, цели и методы математической статистики
Начиная с XVIII века, в общем направлении статистических исследований начинает активно формироваться математическая статистика.
Математическая статистика – раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений.
В зависимости от предмета исследований математическая статистика делится на:
- статистику чисел;
- многомерный статистический анализ;
- анализ функций (процессов) и временных рядов;
- статистику объектов с нечисловыми характеристиками.
В зависимости от цели и методов исследований математическая статистика делится на: описательную статистику; теорию оценивания; теорию проверки гипотез.
| Описательная статистика | Теория оценивания | Теория проверки гипотез | |
| Цель | Обработка и систематизация эмпирических данных | Оценивание ненаблюдаемых данных и сигналов от объектов наблюдения на основе наблюдаемых данных | Обоснование предположений о виде распределения и свойствах случайной величины |
| Методы |
1. Наглядное представление в форме графиков и таблиц. 2. Количественное описание с помощью статистических показателей. |
1. Параметрические методы (наименьших квадратов, максимального правдоподобия и др.). 2. Непараметрические методы. |
1. Последовательный анализ. 2. Статистические критерии. |
Метод выборочных исследований
Статистика получила признание в различных областях человеческой деятельности благодаря заметной экономии времени и прочих ресурсов. Её основная идея: не нужно измерять всё, измерьте только часть всего и сделайте предположение об остальном.
«Всё» в статистике называется генеральной совокупностью.
«Часть всего», которую мы тщательно исследуем, называется выборкой.
Метод выборочных исследований – способ определения свойств группы объектов (генеральной совокупности) на основании статистического исследования её части (выборки).
Например, чтобы оценить средние размеры апельсина, который продаётся в магазине в декабре, необязательно денно и нощно мерить все апельсины во всех ящиках (сколько же для этого нужно времени и людей?!). Достаточно сделать выборку – мерить по одному апельсину из каждого ящика в течение месяца (тут уже и один человек справится).
Статистика предоставляет методику и оценки для того, чтобы правильно провести выборку и на основании знаний о среднем размере апельсина в выборке (выборочной средней) судить о средних размерах всех декабрьских апельсин (генеральной средней).
Средняя арифметическая, простая и взвешенная
Статистическое исследование опирается на собранные данные о каком-то признаке (рост, вес, возраст, доход и т.п.).
Варианта – полученное эмпирическое значение признака.
Вариационный ряд – совокупность собранных вариант.
Пусть мы сделали выборку, провели N измерений и получили x_1,x_2,…,x_N вариант.
Вариационный ряд, состоящий из отдельных вариант, называют дискретным.
Чтобы найти выборочную среднюю дискретного вариационного ряда, нужно вычислить среднюю арифметическую простую:
$$ x_{cp} = frac{1}{N} sum_{i=1}^N x_i ,i = overline{1,N} $$
Знак Σ означает «сумма», i – это индекс полученных вариант, который пробегает все значения, от 1 до N.
Например:
На протяжении четверти школьник получил такие оценки по алгебре: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4. Найдите среднюю оценку за четверть.
Считаем среднюю арифметическую простую:
$$ x_cp = frac{5+4+3+⋯+4}{16} ≈ 4,2 $$
Нетрудно заметить, что оценки повторяются, и вычисления можно упростить, если вместо сложения одинаковых оценок использовать умножение оценок на их количество.
Чтобы найти выборочную среднюю при повторяющихся вариантах, удобно вычислять среднюю арифметическую взвешенную:
$$ x_{cp} = frac{1}{N} sum_{i=1}^K x_i n_i , N = sum_{i=1}^K n_i , i = overline{1,K} $$
где K – количество групп с повторяющимися вариантами, $x_i$ – значение варианты в -й группе, $n_i$ – частота варианты $x_i$.
Например:
Рассматриваем тот же ряд оценок: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4 и составляем таблицу:
$$ x_cp = frac{3cdot3+4cdot7+5cdot6}{3+7+6} ≈ 4,2 $$
Вычисления заметно упростились.
Мода и медиана
Мода дискретного вариационного ряда – это варианта с максимальной частотой. Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
В примере с оценками по алгебре мода $M_0 = 4$ – эта оценка встречается чаще всего, её частота равна 7.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.
Алгоритм:
-
Отсортировать ряд по возрастанию.
-
Если общее количество измерений N нечётное, найти m = $lceil frac{N}{2}rceil$ и округлить в сторону увеличения. $M_e = x_m$ – искомая медиана.
-
Если общее количество измерений N чётное, найти $m = frac{N}{2}$ и вычислить медиану как среднее $M_e = frac{x_m+x_{m+1}}{2}$.
В примере с оценками по алгебре N = 16 – четное. $m = frac{N}{2} = 8 $.
Сортируем ряд оценок по возрастанию: 3,3,3,4,4,4,4, 4,4, 4,5,5,5,5,5,5
$$ x_8 = 4, x_9 = 4 Rightarrow M_e = frac{4+4}{2} = 4 $$
Внимание!
Мода и медиана учитывают индивидуальные варианты и поэтому важны для характеристики вариационного ряда.
Особенное значение мода и медиана приобретают в рядах с выбросами – одиночными очень большими или очень малыми вариантами. В этом случае они оберегают от выводов на основании «средней температуры по больнице».
Примеры
Пример 1. В исследовании месячных доходов десяти человек были получены следующие данные: 200,100,300,300,1000,5000,100,200, 300,400 (дол.).
Найдите выборочную среднюю, моду и медиану.
Почему при оценке доходов мода и медиана предпочтительней выборочной средней?
Составим таблицу:
$x_i$, дол.
100
200
300
400
1000
5000
$sum$
$n_i$, чел.
2
2
3
1
1
1
10
$x_i n_i$
200
400
900
400
1000
5000
7900
Выборочная средняя:$ x_{cp} = frac{7900}{10} = 790$ (дол.)
Мода: $M_o$ = 300 (дол.) – максимальная частота 3
Медиана:
100, 100, 200, 200, 300, 300, 300, 400, 1000, 5000
$$ m = frac{10}{2} = 5, x_5 = x_6 = 300, M_e = frac{300+300}{2} = 300 (дол.) $$
Выборочная средняя не отражает доходов большей части людей в выборке, поскольку даже один человек с большими доходами может резко сместить оценку вправо. Мода и медиана хорошо отражают доходы большей части людей в выборке.
Пример 2. Исследовалось время решения задачи. В исследовании принимало участие 20 человек, из них двое задачу не решили. Время решения остальных участников:
$x_i$, мин
10
15
20
25
30
Найдите выборочную среднюю, моду и медиану.
При подборе задач для контрольной работы, сколько времени следует отвести на решение подобной задачи?
Проведём вычисления:
$x_i$
10
15
20
25
30
$sum$
$x_i n_i$
20
75
100
100
60
355
$$x_cp = frac{355}{18} ≈ 19,7 мин $$
В выборке 2 моды: $M_{o1}$ = 15 мин, $M_{o2}$ = 20 мин
Положение медианы: $m = frac{N}{2} = frac{18}{2} = 9, x_9 = x_10 = 20, Me = 20$ мин
Средняя, одна из мод и медиана равны 20 мин. Поэтому при составлении контрольной следует отвести на подобную задачу 20 мин.
Пример 3. работа по геометрии показала следующие результаты:
Найдите выборочную среднюю, моду и медиану.
Что вы можете сказать об уровне понимания материала?
Проведём вычисления:
$x_i n_i$
10
66
40
10
126
$$x_cp = frac{126}{39} ≈ 3,2$$
Мода: $M_o$ = 3 – эта оценка получена 22 раза
Положение медианы: $m = ⌈ frac{N}{2}⌉ = ⌈frac{39}{2}⌉ = 20, x_{20} = 3, Me = 3$
Средняя, мода и медиана равны 3.
Уровень понимания удовлетворительный, «на троечку».
Вопросы
занятия:
· ввести понятие «среднее арифметическое
числового ряда»;
· ввести понятия «размах ряда», «мода ряда»;
· разобрать, где находят применение рассмотренные
статические характеристики.
Материал
урока
Давайте
рассмотрим пример.
Пример.
Ежедневно
в течение 10 дней в полдень измеряли температуру воздуха (в градусах Цельсия) и
получили следующие данные.
Пользуясь
этим рядом, мы можем определить среднюю температуру воздуха, наблюдаемую в
течение этих десяти дней.
Число
25 называют средним арифметическим рассматриваемого ряда чисел.
Сформулируем
определение.
Определение.
Средним
арифметическим ряда чисел называется частное от деления
суммы этих чисел на число слагаемых.
Таким
образом, умея находить среднее арифметическое ряда чисел, мы можем найти
средний расход холодной воды семьёй в течение года
средний
балл ученика за четверть
среднюю
урожайность пшеницы за последние 5 лет и так далее.
Вернёмся
к нашему примеру. Обратите внимание, что температура воздуха в некоторые дни
существенно отличается от 25 градусов Цельсия (то есть от средней температуры).
Так, самая высокая температура равна 30 градусам, а самая низкая – 19 градусам.
Найдём
разность между наибольшим и наименьшим значениями:
Говорят,
что размах ряда равен 11.
Определение.
Размахом
ряда чисел называется разность между наибольшим и наименьшим
из этих чисел.
Размах
ряда находят, когда хотят узнать, насколько велик разброс данных в ряду. Так,
например, в нашем примере размах ряда показывает колебание температуры воздуха
в течение 10 дней.
Но
кроме среднего арифметического и размаха ряда данных, нас может заинтересовать
вопрос: какая температура воздуха чаще всего устанавливалась за 10 дней?
Заметим, что чаще всего в нашем ряду встречается число 25. Это число называют модой
рассматриваемого ряда.
Сформулируем
определение.
Определение.
Модой
ряда
называется число, которое встречается в данном ряду чаще других.
Стоит
отметить, что ряд может иметь более одной моды.
Например,
Также
ряд может и не иметь моды.
Например,
Моду
ряда находят, когда хотят выяснить некоторый характерный показатель. Например,
удобно воспользоваться этим показателем при изучении спроса покупателей на
мужскую обувь, чтобы определить какой размер самый популярный.
Рассмотрим
ещё один пример.
Пример.
Посмотрите,
среднее арифметическое ряда чисел может не совпадать ни с одним из чисел ряда,
а вот мода всегда совпадает хотя бы с одним из чисел. Причем, если среднее
арифметическое мы можем найти только для числового ряда, то понятие «мода»
относится не только к числовым рядам.
Например,
проведя опрос группы людей, можно определить, какой из видов спорта более
популярен. И модой будут служить те ответы, которые чаще всего встречаются.
Рассмотренные
на уроке характеристики (среднее арифметическое, размах и мода) применяются в
статистике.
Определение.
Статистика
(от латинского слова статус, что означает состояние, положение вещей) – это
наука, которая занимается получением, обработкой и анализом количественных
данных о разнообразных массовых явлениях, происходящих в обществе и
природе.
Основываясь
на примерах, которые мы с вами рассматривали на уроке, можно сказать, что
статистика используется в различных сферах деятельности человека.
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):

(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.

(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):

Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:

(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле

(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:

Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.

- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12

(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13

(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)

8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)

(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.

Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке

