Ме́стное со́лнечное вре́мя может обозначать:
- местное истинное солнечное время, определяемое в месте нахождения наблюдателя видимым положением Солнца на небесной сфере (например, истинный полдень в некоторой точке Земли наступает в момент верхней кульминации Солнца);
- местное среднее солнечное время в некоторой точке на поверхности Земли.
Терминология[править | править код]
В ряде энциклопедических словарей понятие местное солнечное время представлено наименованием местное время и, как правило, с противопоставлением понятию поясное время[1]. Однако в 2011 году в России законом «Об исчислении времени»[2] понятие местное время введено в официальное обращение фактически взамен понятий поясное время и декретное время.
Истинное и среднее солнечное время[править | править код]

Местное среднее солнечное время в городах в один момент в 1853 году
Местное истинное солнечное время определяется положением Солнца. Вследствие того, что орбита, по которой Земля движется вокруг Солнца, не является окружностью, а ось суточного вращения Земли имеет наклон к плоскости орбиты (из-за чего на Земле происходит смена времён года), истинное солнечное время неравномерно. Максимальная разница в продолжительности истинных солнечных суток в течение года составляет примерно 50 с[3], а отклонение времени начала суток от его среднего значения может достигать 16 мин. Это отклонение может быть получено для любого дня года из так называемого уравнения времени[4].
Точно местное истинное солнечное время можно узнать, измерив специальным астрономическим инструментом часовой угол Солнца. Приблизительно солнечное время можно узнать по солнечным часам (низкая точность которых обусловлена размытостью тени).
Местное истинное солнечное время использовалось в жизни обычного человека примерно до XVIII века. К концу XVIII века широкое распространение получили механические часы, конструкция которых всё более совершенствовалась. Различные государства постепенно начали пользоваться средним солнечным временем, предпочитая его истинному, — в Женеве оно было введено с 1780, в Лондоне — с 1792, в Берлине — с 1810, в Париже — с 1816 года[4].
Для городского жителя местное истинное солнечное время — скорее астрономическая абстракция, которая не имеет большого значения в его жизни, поскольку оно неравномерно. Действительно, сложно сделать механические часы, которые идут с переменной скоростью в течение года. Местное среднее солнечное время потеряло актуальность в конце XIX — начале XX века в связи с введением системы часовых поясов и поясного времени.
Расчёты[править | править код]
Расчёт среднего солнечного времени[править | править код]
Поясное (или официальное) время во всех часовых поясах (часовых зонах) сдвинуто на целое число часов (в некоторых странах с добавлением минут) относительно среднего солнечного времени на Гринвичском меридиане, которое называют универсальным и обозначают UTC (Universal Time Coordinated — всемирное координированное время).
От универсального времени отсчитывается не только официальное время в любом часовом поясе, но можно рассчитать и местное среднее солнечное время на любом меридиане.
Например, чтобы узнать среднее солнечное время в центре Москвы, нужно перевести географическую долготу места в часовые единицы: 37°37′ соответствует 2:30:28. Следовательно, среднее солнечное время в центре Москвы отличается от UTC на +2:30:28. С учётом того, что Москва относится к часовому поясу UTC+3:00, средний солнечный полдень в центре Москвы наступает в 12:29:32 по местному поясному времени.
Расчёт истинного времени[править | править код]
Если учесть значение уравнения времени, то можно узнать истинное время на основании точного официального времени, то есть рассчитать положение Солнца без солнечных часов. Формула в общем виде:
,
где 



В некоторых странах официальное время на летний период года сдвигают[5] на один час вперёд. На универсальное время это не влияет (поэтому формула верна и летом), но если универсальное время UTC считать на основании официального, то следует учесть и этот летний час.
Примечания[править | править код]
- ↑ БСЭ 3 изд. том 16. www.bse.uaio.ru. Дата обращения: 8 сентября 2021. Архивировано 8 сентября 2021 года.
- ↑ Федеральный закон от 03.06.2011 N 107-ФЗ (ред. от 05.04.2016) “Об исчислении времени” / КонсультантПлюс. www.consultant.ru. Дата обращения: 19 мая 2016. Архивировано 20 апреля 2016 года.
- ↑ Истинное солнечное время. Научная библиотека. Дата обращения: 8 января 2021. Архивировано 12 января 2021 года.
- ↑ 1 2 Alexey S. Zlygostev , E-Mail webmaster@historic.ru. Гринвичское время для Великобритании: 1825-1880 гг. [1983 Хауз Д. – Гринвичское время и открытие долготы]. 12apr.su. Дата обращения: 3 июня 2016. Архивировано 12 сентября 2015 года.
- ↑ Телеграф «Вокруг Света»: Государственные машины времени. Дата обращения: 30 марта 2011. Архивировано 3 января 2011 года.
На наблюдениях
суточного вращения небесного свода и
годичного движения Солнца, т.е. на
вращении Земли вокруг оси и на обращении
Земли вокруг Солнца, основано измерение
времени.
Любая система
счета времени содержит следующие
основные элементы:
-
периодический
процесс с возможно постоянным периодом; -
метку, по значению
(положению) которой можно судить о
времени; -
начало отсчета
времени; -
единицы измерения
времени.
В астрономии
применяется несколько систем счета
времени, отличающихся вышеперечисленными
элементами.
Рассмотрим самую
простую систему счета времени — звездное
время. Она
основана на вращении Земли вокруг своей
оси, которое можно считать равномерным.
Промежуток времени
между двумя последовательными одноименными
кульминациями точки весеннего
равноденствия на одном и том же
географическом меридиане называется
звездными
сутками.
За начало звездных
суток на данном меридиане принимается
момент верхней кульминации точки
весеннего равноденствия.
Время, протекшее
от верхней кульминации точки весеннего
равноденствия до любого другого ее
положения, выраженное в долях звездных
суток (в звездных часах, минутах и
секундах), называется звездным
временем
s.
Можно показать,
что звездное время s
на данном меридиане в любой момент
численно равно часовому углу точки
весеннего равноденствия t,![]()
выраженному в часовой мере, т.е.
|
s |
(1.18) |
Точка весеннего
равноденствия на небе ничем не отмечена.
Непосредственно измерить ее часовой
угол или заметить момент прохождения
ее через меридиан нельзя. Поэтому
практически для установления начала
звездных суток или звездного времени
в какой-либо момент надо измерить часовой
угол t
какого-либо светила М,
прямое восхождение которого
известно (рис. 1.15).
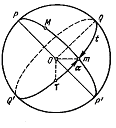
Рис. 1.15.
Связь звездного времени с
и t
светила.
Тогда, поскольку
t
= Qm,
= m,
а часовой угол точки весеннего
равноденствия t
= Q
и, по определению, равен звездному
времени s,
|
s |
(1.19) |
Измерение времени
звездными сутками и их долями наиболее
просто и поэтому весьма выгодно при
решении многих астрономических задач.
Но в повседневной жизни пользоваться
звездным временем крайне неудобно.
Повседневный распорядок жизни человека
связан с видимым положением Солнца над
горизонтом, с его восходом, кульминацией
и заходом, а не с положением фиктивной
точки весеннего равноденствия. А так
как взаимное расположение Солнца и
точки весеннего равноденствия в течение
года непрерывно меняется, то, например,
верхняя кульминация Солнца (полдень) в
разные дни года происходит в разные
моменты звездных суток.
§ 1.13. Истинное и среднее солнечное время. Уравнение времени
Промежуток времени
между двумя последовательными одноименными
кульминациями Солнца (точнее, центра
солнечного диска) на одном и том же
географическом меридиане называется
истинными
солнечными сутками.
За начало истинных солнечных суток на
данном меридиане принимается момент
нижней кульминации Солнца (истинная
полночь).
Время, протекшее
от нижней кульминации Солнца до любого
другого его положения, выраженное в
долях истинных солнечных суток (в
истинных солнечных часах, минутах и
секундах), называется истинным
солнечным временем
T.
Истинное солнечное
время T
на
данном меридиане в любой момент численно
равно часовому углу Солнца t,
выраженному в часовой мере, плюс 12h,
т.е.
|
T |
(1.20) |
Часовой угол
Солнца, когда оно находится над горизонтом
и не закрыто облаками, всегда можно
измерить непосредственно. В момент
верхней кульминации Солнца (в истинный
полдень) t
=
0h,
и следовательно, истинное солнечное
время в полдень всегда равно 12 часам.
Измерение времени
истинными солнечными сутками просто,
но пользоваться истинным солнечным
временем в повседневной жизни так же
неудобно, как и звездным. Неудобство
возникает потому, что продолжительность
истинных солнечных суток — величина
непостоянная. Величина запаздывания
верхней (и нижней) кульминации Солнца
относительно звездного времени в разные
дни года различна. Следовательно,
различна и продолжительность истинных
солнечных суток. Она была бы постоянной,
если бы суточное приращение прямого
восхождения Солнца было постоянным. Но
этого нет по двум причинам:
1) Солнце движется
не по небесному экватору, а по эклиптике,
наклоненной к небесному экватору на
значительный угол
= 23°26′.
2) Движение Солнца
по эклиптике неравномерно.
В результате
действия обеих причин истинные солнечные
сутки, например, 22 декабря, длиннее на
50-51 секунду, чем 23 сентября. Непостоянство
продолжительности истинных солнечных
суток не позволяет применять их для
счета времени на практике.
Истинные солнечные
сутки продолжительнее звездных суток
примерно на 4 минуты из-за того, что
Солнце движется по эклиптике навстречу
суточному движению неба.
Чтобы получить
сутки постоянной продолжительности, и
в то же время связанные с движением
Солнца, в астрономии введено понятие
фиктивной точки — среднего
экваториального
солнца. Среднее экваториальное солнце
равномерно движется по небесному
экватору с постоянной скоростью, равной
средней скорости движения Солнца по
эклиптике.
Введением среднего
экваториального солнца, у которого
суточные приращения
прямого восхождения одинаковы, устраняется
непостоянство продолжительности
солнечных суток и неравномерность
истинного солнечного времени.
Промежуток времени
между двумя последовательными одноименными
кульминациями среднего экваториального
солнца на одном и том же географическом
меридиане называется средними
солнечными сутками
или просто средними
сутками.
Из определения среднего экваториального
солнца следует, что продолжительность
средних солнечных суток равна среднему
значению продолжительности истинных
солнечных суток за год.
За начало средних
солнечных суток на данном меридиане
принимается момент нижней кульминации
среднего экваториального солнца (средняя
полночь).
Время, протекшее от нижней кульминации
среднего экваториального солнца до
любого другого его положения, выраженное
в долях средних солнечных суток (в
средних часах, минутах и секундах),
называется средним
солнечным временем
или просто средним
временем
Tm
.
Среднее время Tm
на данном меридиане в любой момент
численно равно часовому углу tm
среднего экваториального солнца,
выраженному в часовой мере, плюс 12h,
т.е.
|
Tm |
(1.21) |
Среднее экваториальное
солнце на небе ничем не отмечено, поэтому
измерить его часовой угол нельзя, и
среднее солнечное время получают путем
вычислений по определенному из наблюдений
истинному солнечному или звездному
времени.
Разность между
средним временем и истинным солнечным
временем в один и тот же момент называется
уравнением
времени
.
На основании (1.20) и (1.21) уравнение
времени
|
= Tm |
(1.22) |
Из последнего соотношения следует:
|
Tm |
(1.23) |
т.е.
среднее
солнечное время в любой момент равно
истинному солнечному времени плюс
уравнение времени.
Таким образом,
измерив непосредственно часовой угол
Солнца t,
определяют
истинное солнечное время и, зная уравнение
времени
в этот
момент, находят среднее солнечное время.
Так как среднее
экваториальное солнце проходит через
небесный меридиан то раньше, то позже
истинного Солнца, разность их часовых
углов (уравнение времени) может быть
как положительной, так и отрицательной
величиной.
Уравнение времени
обращается в нуль около 15 апреля, 14 июня,
1 сентября и 24 декабря и четыре раза в
году принимает экстремальные значения;
из них наиболее значительные около 11
февраля (
= +14m)
и 2 ноября (
= 16m).
Уравнение времени
можно вычислить для любого момента. Оно
обычно публикуется в астрономических
календарях и ежегодниках для каждой
средней полуночи на меридиане Гринвича.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На протяжении всей истории человечества времени отводилась важная роль. Время в астрономии, как и в любой сфере, играет важную и интересную роль. В своем роде, это продолжительность любого действия, оценка самой жизнидеятельности. Представьте, если бы его не было, то как бы мы определяли все вокруг.

Юлианские дни
Астрономы приняли определенную порядковую нумерацию дней. В ней существует цикл длиной 28 лет. В нём все дни и недели повторяются.

Данный способ измерения разработан Джоном Гершелем в 1849 году. Счёт времени начался с полудня 1 апреля с 4713 года до нашей эры. А предложил его использовать Иосиф Скалигер. Кстати, он и назвал его юлианским, в честь отца Юлия

«Вселенная и время бесконечны. Значит любое событие неизбежно, даже невозможное»
из фильма Трасса 60
Звёздное время в астрономии
Звёздные сутки соответствуют дистанции между двумя последовательными вершинами.
Такое время в астрономии можно определить как часовой угол точки весеннего равноденствия. Более того, по этому месту отсчитывают звёздное время.
Звёздные сутки подразумевают продолжительность оборота Земли вокруг своей оси. Их делят на часы, минуты и секунды. В одном году звездных суток больше на один, чем в средних солнечных.
Как видно, звёздные сутки короче, чем средние солнечные. Установленная разница составляет 3 минуты 56 секунд.
Притом, время обращения Земли к точке весеннего равноденствия всегда одно и то же. Итак, сутки постоянны.
Солнечное время в астрономии
Применение звёздного времени удобно в астрономии, но не для обыденной жизни человека. Поэтому было принято такое понятие как солнечное время.
Этот отрезок времени зависит от изменения часового угла Солнца.
Данный порядок расчёта времени основан на интервале между двумя последовательными кульминациями Солнца. Кстати, большую роль играет были эти кульминации верхними или нижними. От этого различают полдень сейчас или полночь.
Истинное и среднее солнечное время в астрономии
Солнечное время бывает истинным и средним. Зависит это того, по какому Солнцу его определяют.
Истинные солнечные сутки это время оборота Земли касательно Солнца.
Началом таких суток принято считать истинную полночь, то есть период нижней кульминации Солнца.

Передвижение солнца неравномерно. В результате этого, солнечные сутки 22 декабря длиннее, чем 23 сентября почти на одну минуту. Но такая неточность неудобна для расчёта.
В нашей жизни сутки составляют 24 часа. Как правило, измеряют всё в секундах. Кроме того, для определения времени человек различает утро, день, вечер и ночь. Это зависит, прежде всего, от того, где расположено Солнце относительно отдельного меридиана.
А вот средние солнечные сутки используются для точного определения времени.
Это время между двумя относительными кульминациями среднего экваториального Солнца на одном меридиане. Лучше сказать, что средние солнечные сутки соответствуют среднему значению истинных солнечных.
Эклиптическое Солнце размеренно двигается со средней скоростью Солнца. Сходятся они примерно 3 января и 4 июля.
Экваториальное также равномерно, но совпадает с эклиптическим солнцем в точке весеннего равноденствия. Среднее экваториальное солнце постоянно и равномерно относительно истинному солнечному времени.

Поясное время
В общем, используется оно в основном в географии.
Из школьных знаний нам известно, что Земля делится на меридианы. Всего их 24 и они отстают друг от друга на 15 градусов долготы.
Принято считать, что начальный меридиан с нулевой долготой является основным. Его ещё называют всемирным.
Меридианы простираются с запада на восток.
Такое время в соседних поясах отличается на один час. Для того, чтобы вычислить время отдельного пояса, необходимо узнать номер пояса.

Собственно говоря, поясное время это время часового пояса. Принято считать, что день состоит из 24 часов и начинается в полночь.
Декретное время
Например, на территории России выделено на 9 часовых поясов. В 1930 году определили понятие декретного времени. К поясному добавили один час.

Декретное время также называют московским.
Это определение времени по подразумевает использование времени соседнего пояса. Иначе говоря, декретное время это поясное время плюс один час.
По новым понятиям его называют местным временем.
Эфемеридное время
Это шкала времени, определяющая секунды. Расчёт такого времени не зависит от скорости вращения Земли.
Вдобавок, оно является основной единицей времени. Ввел это понятие в 1952 году Дж. М. Клеменс.
Эфемеридное время постоянно и применяется, на самом деле, для удобства исчисления.
«Отнять у человека час времени, отнять у человека жизнь-разница в масштабах»
Франк Герберт
Как видно, время отражает продолжительность чего-либо. Надо полагать, это самое уникальное течение и величина, которую определил человек. Помимо всего, для его расчёта придумали множество способов.

Безусловно, время очень много значит для человека. Так как это одна из основных составляющих его жизни.
Что будет дальше покажет нам время.
![]()
From Wikipedia, the free encyclopedia
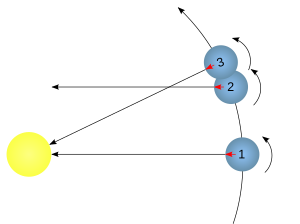
On a prograde planet like the Earth, the sidereal day is shorter than the solar day. At time 1, the Sun and a certain distant star are both overhead. At time 2, the planet has rotated 360° and the distant star is overhead again (1→2 = one sidereal day). But it is not until a little later, at time 3, that the Sun is overhead again (1→3 = one solar day). More simply, 1-2 is a complete rotation of the Earth, but because the revolution around the Sun affects the angle at which the Sun is seen from the Earth, 1-3 is how long it takes noon to return. [Note that in this diagram, the relative motion, and corresponding angles, are highly exaggerated for illustrative purposes.]
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Traditionally, there are three types of time reckoning based on astronomical observations: apparent solar time and mean solar time (discussed in this article), and sidereal time, which is based on the apparent motions of stars other than the Sun.[1]
Introduction
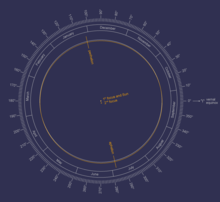
The Earth’s orbit around the Sun, showing its eccentricity
A tall pole vertically fixed in the ground casts a shadow on any sunny day. At one moment during the day, the shadow will point exactly north or south (or disappear when and if the Sun moves directly overhead). That instant is local apparent noon, or 12:00 local apparent time. About 24 hours later the shadow will again point north–south, the Sun seeming to have covered a 360-degree arc around Earth’s axis. When the Sun has covered exactly 15 degrees (1/24 of a circle, both angles being measured in a plane perpendicular to Earth’s axis), local apparent time is 13:00 exactly; after 15 more degrees it will be 14:00 exactly.
The problem is that in September the Sun takes less time (as measured by an accurate clock) to make an apparent revolution than it does in December; 24 “hours” of solar time can be 21 seconds less or 29 seconds more than 24 hours of clock time. This change is quantified by the equation of time, and is due to the eccentricity of Earth’s orbit (as in, Earth’s orbit is not perfectly circular, meaning that the Earth–Sun distance varies throughout the year), and the fact that Earth’s axis is not perpendicular to the plane of its orbit (the so-called obliquity of the ecliptic).
The effect of this is that a clock running at a constant rate – e.g. completing the same number of pendulum swings in each hour – cannot follow the actual Sun; instead it follows an imaginary “mean Sun” that moves along the celestial equator at a constant rate that matches the real Sun’s average rate over the year.[2] This is “mean solar time”, which is still not perfectly constant from one century to the next but is close enough for most purposes. As of 2008, a mean solar day is about 86,400.002 SI seconds.[3]
Apparent solar time
The apparent sun is the true sun as seen by an observer on Earth.[4] Apparent solar time or true solar time[a] is based on the apparent motion of the actual Sun. It is based on the apparent solar day, the interval between two successive returns of the Sun to the local meridian.[5][6] Apparent solar time can be crudely measured by a sundial. The equivalent on Mars is termed Mars local true solar time (LTST).[7][8]
The length of a solar day varies through the year, and the accumulated effect produces seasonal deviations of up to 16 minutes from the mean. The effect has two main causes. First, due to the eccentricity of Earth’s orbit, Earth moves faster when it is nearest the Sun (perihelion) and slower when it is farthest from the Sun (aphelion) (see Kepler’s laws of planetary motion). Second, due to Earth’s axial tilt (known as the obliquity of the ecliptic), the Sun’s annual motion is along a great circle (the ecliptic) that is tilted to Earth’s celestial equator. When the Sun crosses the equator at both equinoxes, the Sun’s daily shift (relative to the background stars) is at an angle to the equator, so the projection of this shift onto the equator is less than its average for the year; when the Sun is farthest from the equator at both solstices, the Sun’s shift in position from one day to the next is parallel to the equator, so the projection onto the equator of this shift is larger than the average for the year (see tropical year). In June and December when the sun is farthest from the celestial equator, a given shift along the ecliptic corresponds to a large shift at the equator. Therefore, apparent solar days are shorter in March and September than in June or December.
| Date | Duration in mean solar time |
|---|---|
| February 11 | 24 hours |
| March 26 | 24 hours − 18.1 seconds |
| May 14 | 24 hours |
| June 19 | 24 hours + 13.1 seconds |
| July 25/26 | 24 hours |
| September 16 | 24 hours − 21.3 seconds |
| November 2/3 | 24 hours |
| December 22 | 24 hours + 29.9 seconds |
These lengths will change slightly in a few years and significantly in thousands of years.
Mean solar time
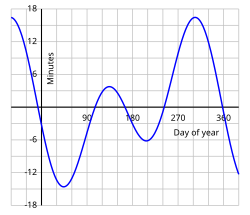
The equation of time—above the axis a sundial will appear fast relative to a clock showing local mean time, and below the axis a sundial will appear slow.
Mean solar time is the hour angle of the mean Sun plus 12 hours. This 12 hour offset comes from the decision to make each day start at midnight for civil purposes, whereas the hour angle or the mean sun is measured from the local meridian.[10] As of 2009, this is realized with the UT1 time scale, constructed mathematically from very-long-baseline interferometry observations of the diurnal motions of radio sources located in other galaxies, and other observations.[11]: 68, 326 [12] The duration of daylight varies during the year but the length of a mean solar day is nearly constant, unlike that of an apparent solar day.[13] An apparent solar day can be 20 seconds shorter or 30 seconds longer than a mean solar day.[9][14] Long or short days occur in succession, so the difference builds up until mean time is ahead of apparent time by about 14 minutes near February 6, and behind apparent time by about 16 minutes near November 3. The equation of time is this difference, which is cyclical and does not accumulate from year to year.
Mean time follows the mean sun. Jean Meeus describes the mean sun as follows:
Consider a first fictitious Sun travelling along the ecliptic with a constant speed and coinciding with the true sun at the perigee and apogee (when the Earth is in perihelion and aphelion, respectively). Then consider a second fictitious Sun travelling along the celestial equator at a constant speed and coinciding with the first fictitious Sun at the equinoxes. This second fictitious sun is the mean Sun[15]
The length of the mean solar day is slowly increasing due to the tidal acceleration of the Moon by Earth and the corresponding slowing of Earth’s rotation by the Moon.
History

The sun has always been visible in the sky, and its position forms the basis of apparent solar time, the timekeeping method used in antiquity. An Egyptian obelisk constructed c. 3500 BC,[16] a gnomon in China dated 2300 BC,[17] and an Egyptian sundial dated 1500 BC[18] are some of the earliest methods for measuring the sun’s position.
Babylonian astronomers knew that the hours of daylight varied throughout the year. A tablet from 649 BC shows that they used a 2:1 ratio for the longest day to the shortest day, and estimated the variation using a linear zigzag function.[19] It is not clear if they knew of the variation in the length of the solar day and the corresponding equation of time. Ptolemy clearly distinguishes the mean solar day and apparent solar day in his Almagest (2nd century), and he tabulated the equation of time in his Handy Tables.[20]
Apparent solar time grew less useful as commerce increased and mechanical clocks improved. Mean solar time was introduced in almanacs in England in 1834 and in France in 1835. Because the sun was difficult to observe directly due to its large size in the sky, mean solar time was determined as a fixed ratio of time as observed by the stars, which used point-like observations. A specific standard for measuring “mean solar time” from midnight came to be called Universal Time.[11]: 9–11
Conceptually Universal Time is the rotation of the Earth with respect to the sun and hence is mean solar time. However, UT1, the version in common use since 1955, uses a slightly different definition of rotation that corrects for the motion of Earth’s poles as it rotates. The difference between this corrected mean solar time and Coordinated Universal Time (UTC) determines whether a leap second is needed. (Since 1972 the UTC time scale has run on SI seconds, and the SI second, when adopted, was already a little shorter than the current value of the second of mean solar time.[21][11]: 227–231 )
See also
- Local mean time
- Meridian circle
- Earth rotation
- Synodic day
Notes
- ^ ‘apparent’ is commonly used in English-language sources, but ‘true’ is used in French astronomical literature and has become nearly as common in English sources. See:
- Vince, Samuel (1797). A Complete System Of Astronomy Vol 1. Cambridge University Press. p. 44.
What we call apparent time the French call true
- “Comprendre – Concepts fondamentaux – Echelles de temps”. Bureau des Longitudes (in French). November 23, 2009. Archived from the original on November 23, 2009.
temps vrai [true time]
- Allison, Michael; Schmunk, Robert (June 30, 2015). “Technical Notes on Mars Solar Time as Adopted by the Mars24 Sunclock”. Goddard Institute for Space Studies. National Aeronautics and Space Administration. Archived from the original on September 25, 2015. Retrieved October 8, 2015.
the solar hour angle or True Solar Time (TST)
- Vince, Samuel (1797). A Complete System Of Astronomy Vol 1. Cambridge University Press. p. 44.
References
- ^ For the three kinds of time, see (for example) the explanatory section in the almanac Connaissance des Temps for 1902, page 759 Archived August 10, 2011, at the Wayback Machine.
- ^ “solar time, mean”. Glossary, Astronomical Almanac Online. Her Majesty’s Nautical Almanac Office and the United States Naval Observatory. 2021.
- ^ “Leap Seconds”. Time Service Department, United States Naval Observatory. 1999. Archived from the original on March 12, 2015.
- ^ Tatum, J.B. (March 27, 2022). “Celestial Mechanics Chapter 6” (PDF). University of Victoria. Archived (PDF) from the original on September 23, 2015.
- ^ “solar time, apparent”. Glossary, Astronomical Almanac Online. Her Majesty’s Nautical Almanac Office and the United States Naval Observatory. 2021.
- ^ Yallop, B. D.; Hohenker, C. Y. (August 1989). “Astronomical Information Sheet No. 58” (PDF). HM Nautical Almanac Office. Solar Location Diagram.
- ^ Allison, Michael; Schmunk, Robert (June 30, 2015). “Technical Notes on Mars Solar Time as Adopted by the Mars24 Sunclock”. Goddard Institute for Space Studies. National Aeronautics and Space Administration. Archived from the original on September 25, 2015. Retrieved October 8, 2015.
- ^ Allison, Michael; McEwen, Megan (2000). “A post-Pathfinder evaluation of areocentric solar coordinates with improved timing recipes for Mars seasonal/diurnal climate studies”. Planetary and Space Science. 48 (2–3): 215. Bibcode:2000P&SS…48..215A. doi:10.1016/S0032-0633(99)00092-6. hdl:2060/20000097895. S2CID 123014765. Archived from the original on June 23, 2015.
- ^ a b Jean Meeus (1997), Mathematical astronomy morsels (Richmond, VA: Willmann-Bell) 346. ISBN 0-943396-51-4.
- ^ Hilton, James L; McCarthy, Dennis D. (2013). “Precession, Nutation, Polar Motion, and Earth Rotation”. In Urban, Sean E.; Seidelmann, P. Kenneth (eds.). Explanatory Supplement to the Astronomical Almanac (3rd ed.). Mill Valley, CA: University Science Books. ISBN 978-1-891389-85-6.
- ^ a b c McCarthy, D. D.; Seidelmann, P. K. (2009). TIME From Earth Rotation to Atomic Physics. Weinheim: Wiley-VCH Verlag GmbH & Co. KGa. ISBN 978-3-527-40780-4.
- ^ Capitaine, N.; Wallace, P. T.; McCarthy, D. D. (2003). “Expressions to implement the IAU 2000 definition of UT1”. Astronomy and Astrophysics. 406 (3): 1135–1149. Bibcode:2003A&A…406.1135C. doi:10.1051/0004-6361:20030817. S2CID 54008769. (or in pdf form); and for some earlier definitions of UT1 see Aoki, S.; Guinot, B.; Kaplan, G. H.; Kinoshita, H.; McCarthy, D. D.; Seidelmann, P. K. (1982). “The new definition of universal time”. Astronomy and Astrophysics. 105 (2): 359–361. Bibcode:1982A&A…105..359A.
- ^ For a discussion of the slight changes that affect the mean solar day, see the ΔT article.
- ^ Ricci, Pierpaolo. “The duration of the true solar day”. pierpaoloricci.it. Archived from the original on August 26, 2009.
- ^ Meeus, J. (1998). Astronomical Algorithms. 2nd ed. Richmond VA: Willmann-Bell. p. 183.
- ^ “A Walk Through Time – Early Clocks”. A Walk Through Time – The Evolution of Time Measurement through the Ages. National Institute of Standards and Technology. August 12, 2009.
- ^ Li, Geng (2015). “Gnomons in Ancient China”. In Ruggles, C. (ed.). Handbook of Archaeoastronomy and Ethnoastronomy. pp. 2095–2104. Bibcode:2015hae..book.2095L. doi:10.1007/978-1-4614-6141-8_219. ISBN 978-1-4614-6140-1.
- ^ Vodolazhskaya, L.N. (2014). “Reconstruction of ancient Egyptian sundials” (PDF). Archaeoastronomy and Ancient Technologies. 2 (2): 1–18.
- ^ Pingree, David; Reiner, Erica (1974). “A Neo-Babylonian Report on Seasonal Hours”. Archiv für Orientforschung. 25: 50–55. ISSN 0066-6440. JSTOR 41636303.
- ^ Neugebauer, Otto (1975), A History of Ancient Mathematical Astronomy, New York / Heidelberg / Berlin: Springer-Verlag, pp. 984–986, ISBN 978-0-387-06995-1
- ^ :(1) In “The Physical Basis of the Leap Second”, by D D McCarthy, C Hackman and R A Nelson, in Astronomical Journal, vol.136 (2008), pages 1906-1908, it is stated (page 1908), that “the SI second is equivalent to an older measure of the second of UT1, which was too small to start with and further, as the duration of the UT1 second increases, the discrepancy widens.” :(2) In the late 1950s, the cesium standard was used to measure both the current mean length of the second of mean solar time (UT2) (result: 9192631830 cycles) and also the second of ephemeris time (ET) (result:9192631770 ± 20 cycles), see “Time Scales”, by L. Essen Archived October 19, 2008, at the Wayback Machine, in Metrologia, vol.4 (1968), pp.161-165, on p.162. As is well known, the 9192631770 figure was chosen for the SI second. L Essen in the same 1968 article (p.162) stated that this “seemed reasonable in view of the variations in UT2”.
External links
- Sunrise and Sunset and maximum Sun altitude, all year long, anywhere
- Astrarium Solar Tempometer: Apparent solar time in a digital display.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Система истинного солнечного времени (или истинное солнечное время – m ) применяется при астрономических или геодезических наблюдениях Солнца. Параметры системы:
1. Механизм – вращение Земли вокруг своей оси;
2. Масштаб – истинные солнечные сутки – промежуток времени между двумя последовательными нижними кульминациями центра истинного Солнца;
3. Начальная точка – центр диска истинного Солнца – нуль пункт – истинная полночь, или момент нижней кульминации центра диска истинного Солнца;
4. Способ отсчета. Мера измерения истинного солнечного времени – геоцентрический часовой угол истинного Солнца t плюс 12 часов:
m= t + 12h.
Единица истинного солнечного времени – секунда, равная 1 / 86 400 истинных солнечных суток, не удовлетворяет основному требованию, предъявляемому к единице измерения времени – она непостоянна.
Причинами непостоянства шкалы истинного солнечного времени являются:
1. Неравномерное движение Солнца по эклиптике вследствие эллиптичности орбиты Земли;
2. Неравномерное возрастание прямого восхождения Солнца в течение года, так как Солнце движется по эклиптике, наклоненной к небесному экватору под углом примерно 23,5о.
Вследствие этих причин применение системы истинного солнечного времени на практике неудобно. Переход к равномерной шкале солнечного времени происходит в два этапа.
Этап 1 − переход к фиктивному среднему эклиптическому Солнцу. На данном этапе исключается неравномерность движения Солнца по эклиптике. Неравномерное движение по эллиптической орбите заменяется равномерным движением по круговой орбите. Истинное Солнце и среднее эклиптическое Солнце совпадают, когда Земля проходит через перигелий и афелий своей орбиты.
Этап 2 − переход к среднему экваториальному Солнцу, движущемуся равномерно вдоль небесного экватора. Здесь исключается неравномерность возрастания прямого восхождения Солнца, обусловленная наклоном эклиптики. Истинное Солнце и среднее экваториальное Солнце одновременно проходят точки весеннего и осеннего равноденствия. В результате перечисленных действий вводится новая система измерения времени – среднее солнечное время. Среднее солнечное время обозначается m.
Параметрами системы среднего солнечного времени являются:
1. Механизм – вращение Земли вокруг оси;
2. Масштаб – средние сутки – промежуток времени между двумя последовательными нижними кульминациями среднего экваториального Солнца экв;
3. Начальная точка – среднее экваториальное Солнце экв, нульпункт – средняя полночь, или момент нижней кульминации среднего экваториального Солнца;
4. Способ отсчета. Мерой измерения среднего времени является геоцентрический часовой угол среднего экваториального Солнца t экв плюс 12 часов: m = t экв + 12h.
Определить среднее солнечное время непосредственно из наблюдений нельзя, так как среднее экваториальное Солнце – фиктивная точка на небесной сфере. Среднее солнечное время вычисляют по истинному солнечному времени, определенному из наблюдений истинного Солнца. Разность истинного солнечного времени m и среднего солнечного времени m называется уравнением времени и обозначается η:
η = m – m = t– t ср.экв.
Уравнение времени выражается двумя синусоидами с годовым и полугодовым периодами:
η = η1 + η2 ≈ –7,7msin (l + 79о) + 9,5m sin 2l,
где l – эклиптическая долгота среднего эклиптического Солнца. График η есть кривая с двумя максимумами и двумя минимумами (рис.1). Значения уравнения времени лежат в пределах от +14m до –16m.
В Астрономическом Ежегоднике на каждую дату приводится величина Е:
Е = η + 12h .
С данной величиной связь между средним солнечным временем и часовым углом истинного Солнца определяется выражением:
m = t – E.
Рис 1. График уравнивания времени
Литература:
-
Кононович Э.В., Мороз В.И. Общий курс астрономии: Учебное пособие / под ред. В.В. Иванова. – М.: Едиториал УРСС, 2001;
-
Астрономический ежегодник на 2014 год. – СПб.: Наука, 2013;
- Л.И. Машонкина, В.Ф. Сулейманов. Задачи и Упражнения по Общей Астрономии: Методическое пособие к практикуму по Общей астрономии, Казань, 2002;
-
Труды ИПА РАН. Вып. 10. В.А. Брумберг, Н.И. Глебова, М.В. Лукашева, А.А. Малков, Е.В. Питьева, Л.И. Румянцева, М.Л. Свешников, М.А. Фурсенко. Расширенное объяснение к «Астрономическому ежегоднику». – СПб.: ИПА РАН, 2004.
