Как найти среднее время безотказной работы элемента - Сайт, где вы сможете решить свои вопросы

Плотность
распределения времени безотказной
работы f(t)
– это плотность распределения случайной
величины Т. Она наиболее полно характеризует
Надежность техники в данный момент
(точечная характеристика). По ней можно
определить любой показатель надежности
невосстанавливаемой системы. В этом
состоит достоинство плотности
распределения времени безотказной
работы.

Производная
от вероятности отказа по времени есть
плотность
вероятности, или дифференциальный закон
распределения времени работы объекта
до отказа, т.е.

(5)

Полученная
математическая связь позволяет записать:

;
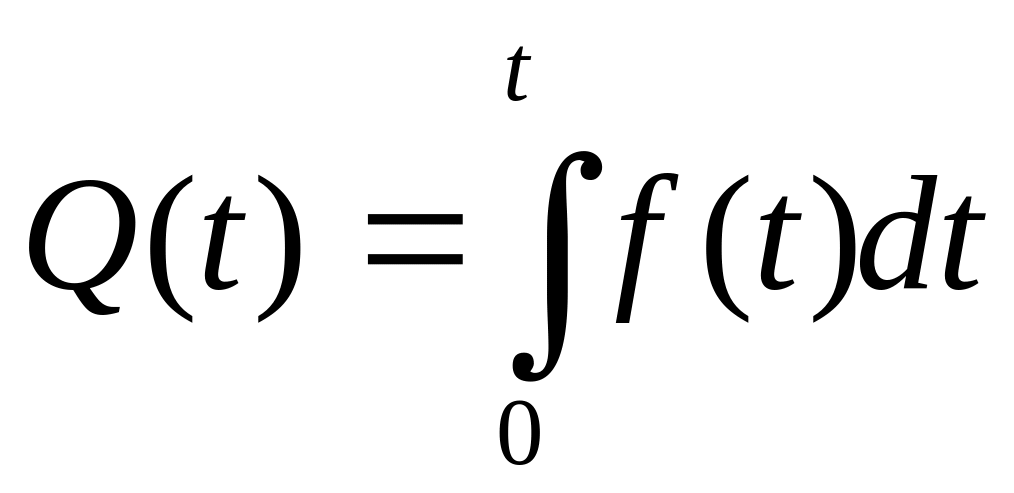
(6)

Таким
образом, зная плотность вероятности
f(t),
легко найти искомую величину P(t) и Q(t).

Соотношения
(6) имеют место при любом законе
распределения времени возникновения
отказов.

Достоинством
является следующее. Как плотность
распределения вероятности, она наиболее
полно характеризует случайное время
возникновения отказов и по ней легко
определить вероятность безотказной
работы, математическое ожидание,
дисперсию и другие удобные характеристики
распределения.

К
недостаткам плотности
вероятности f(t)
следует отнести то, что она характеризует
надежность аппаратуры до первого отказа.
Оценить с помощью частоты отказа
надежность аппаратуры длительного
пользования, которая может ремонтироваться,
затруднительно. В общем случае надежность
аппаратуры длительного пользования
обычно характеризуется средней частотой
отказа.

Под
частотой отказов элементов понимают
отношение числа отказавших образцов
техники в единицу времени к числу
испытуемых образцов при условии, что
отказавшие образцы не восполняются
исправными:

,
(7)

где
n(t, t+∆t)
– число отказавших образцов за промежуток
времени (t, t+∆t);
N₀ – число образцов,
первоначально поставленных на испытания;
∆t – длина промежутка
времени.

Так как число
отказавших образцов в интервале времени
может
зависеть от расположения этого промежутка
по оси времени, то частота отказов
является функцией времени t.

Соотношение
(7) следует из того, что f(t)=Q’(t)=–P’(t),
а для малых значений ∆t

Если
N(t) – число
исправных образцов к моменту времени
t, а N(t+
∆t) – число исправных
образцов к моменту времени t+∆t,
то

На
практике достаточно часто приходится
определять условную вероятность
безотказной работы объекта в заданном
интервале времени Р(t₁,t₂)
при условии, что в момент времени t₁
объект работоспособен и известны Р (t₁)
и Р (t₂).
По формуле вероятности совместного
появления двух зависимых событий

откуда

(*)

По
известным статистическим данным можно
записать:

(**)

где
N(t₁),
N(t₂)
– число объектов, работоспособных
соответственно к моментам времени t₁
и t_2,т.е.
N(t₁)=N₀– n(t₁);
N(t₂)=N₀– n(t₂).

3. Среднее время безотказной работы (средняя наработка до отказа)

Средним
временем безотказной работы
(средней наработкой
до отказа) T₁называется
математическое ожидание времени
безотказной работы технического объекта
(наработки объекта до первого отказа):

T₁=M(T).

Как математическое ожидание
случайной величины с плотностью f(t),
среднее время безотказной работы
вычисляется по формуле:

Используя
известную связь между f(t), Q(t) и P(t), запишем:

Интегрируя
по частям, получим:

Учитывая,
что Р(0) = 1, P(+)=0,
полагая, что

,
получим:

.
(8)

Таким
образом, средняя наработка до отказа
равна площади, образованной кривой
вероятности безотказной работы P(t) и
осями координат.

Среднее
время безотказной работы является
интегральным показателем надежности.
Его основное достоинство — высокая
наглядность. Недостаток этого
показателя в том, что он, будучи
интегральным, характеризует надежность
техники длительного времени работы.

По
статистическим данным об отказах T₁
определяется по формуле:

(9)

где N_o
– число испытуемых образцов техники (в
начале испытания); t_j
– время безотказной работы j-го образца.

Из выражения
(9) видно, что для определения среднего
времени безотказной работы необходимо
знать времена отказов всех образцов,
над которыми производятся испытания.
Поэтому при большом числе образцов
предпочитают пользоваться формулой

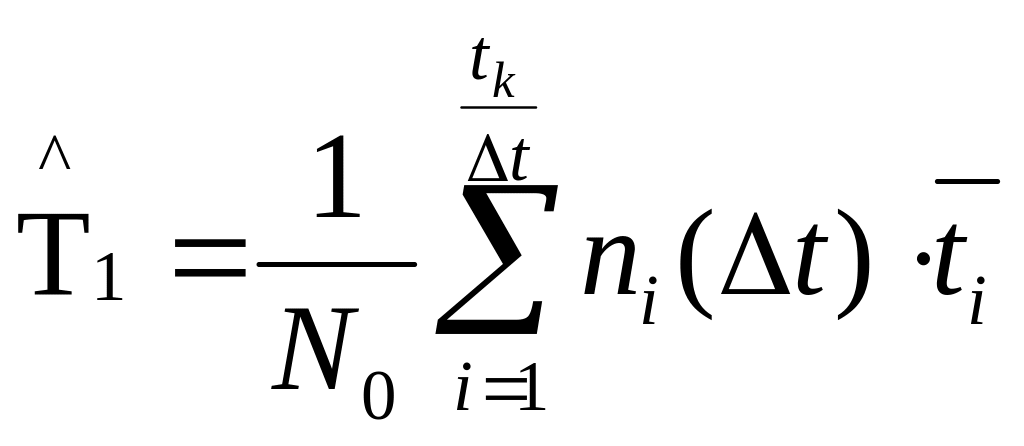
(10)

где n_i(t)
– число образцов, отказавших в i -том
интервале;

–
среднее время i-го интервала ();

t_k–
время, в течение которого отказали все
N₀ образцов;

t
– выбранная величина интервала времени.

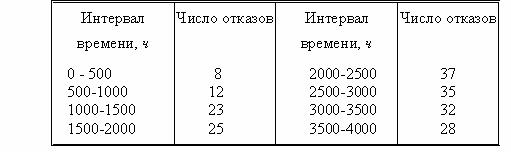
Пример. В
процессе эксплуатации приборов одного
типа учитывалось число вышедших из
строя приборов в течении каждых 500 часов
работы, при этом наблюдение велось за
200 одинаковыми приборами (=200).
в результате подсчета отказавших
приборов получены данные, сведенные в
табл.1.

По данным табл.1,
пользуясь формулой (2), определим
вероятность безотказной работы прибора
к любому моменту времени:

Таблица 1.

Количество
отказов приборов в i-ом интервале времени

Воспользовавшись
формулой (4), определим вероятность
отказа приборов, например, для тех же
моментов времени:

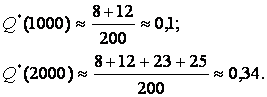
Определим также
среднюю наработку до отказа приборов
по формуле (10):

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как вычисляется среднее время до отказа и вероятность безотказной работы?

Время на прочтение
4 мин

Количество просмотров 118K

Понятиям MTTF (Mean Time To Failure — среднее время до отказа) и другим терминам теории надежности посвящено большое количество статей, в том числе на Хабре (см., например, тут). Вместе с тем, редкие публикации «для широкого круга читателей» затрагивают вопросы математической статистики, и уж тем более они не дают ответа на вопрос о принципах расчета надежности электронной аппаратуры по известным характеристикам ее составных элементов.

В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).

1. Теория: основные характеристики отказоустойчивости
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).

Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.

Ключевое понятие теории надежности — это понятие отказа, измеряемое, соответственно, интервальным показателем
Q(t) = вероятность того, что изделие откажет к моменту времени t.
Соотвественно, вероятность безотказной работы (ВБР, в английской терминологии «reliability»):
P(t) = вероятность того, что изделие проработает без отказа от момента t₀=0 до момента времени t.
По определению, в момент t₀=0 изделие находится в работоспособном состоянии, т.е. Q(0)=0, а P(0)=1.

Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.

И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.

Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).

Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).

А вот при чем.

2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).

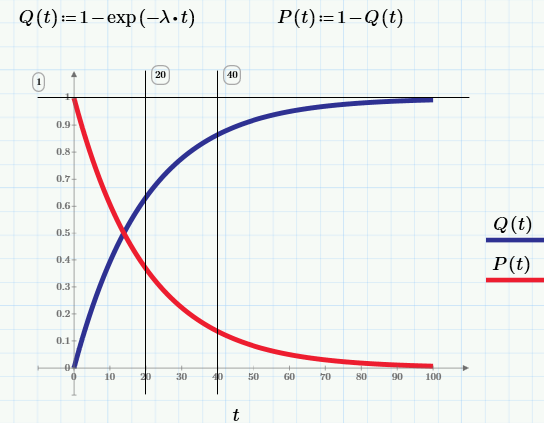
Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
,
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.

Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.

Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.

Все это замечательные свойства экспоненциального распределения. Почему мы выбрали в качестве для описания отказов именно его? Да потому что это наиболее простая модель – модель пуассоновского потока событий, которая уже была нами рассмотрена в статье про анализ конверсии сайта. Поэтому-то в теории надежности наиболее часто используется показательное (экспоненциальное) распределение, для которого, как мы выяснили:

надежность элементов можно оценить одним числом, т.к. λ=const;
по известной λ довольно просто оценить остальные показатели надежности (например, ВБР для любого времени t);
λ обладает хорошей наглядностью
λ нетрудно измерить экспериментально

Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).

Источник

Средним временем безотказной работы называется математическое ожидание времени безотказной работы.

Эта характеристика надежности обозначается T. Как всякое математическое ожидание случайной величины среднее время безотказной работы определяется из выражения:

. (1.25)

Приведенное определение является вероятностным. Для определения среднего времени безотказной работы из статистических данных пользуются формулой:

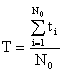, (1.26)

где t_i– время безотказной работы i-го образца, N₀– число образцов, над которыми проводится испытание.

Из выражения (1.26) видно, что для определения T необходимо знать моменты отказов всех образцов аппаратуры, над которыми проводится эксперимент. При большом числе образцов N₀ это может сильно усложнить эксперимент.

Выражение (1.26) является статистическим определением среднего времени безотказной работы.

Среднее время безотказной работы является одной из наиболее наглядных количественных характеристик надежности. Однако этой характеристике надежности свойственны существенные недостатки. Как математическое ожидание случайной величины, она не может полностью характеризовать время работы аппаратуры. Необходимо еще знать, по меньшей мере, дисперсию времени отказов аппаратуры. Кроме того, T фактически не позволяет оценить надежность аппаратуры, время работы которой во много раз меньше среднего времени безотказной работы.

Из выражения (1.26) видно, что для вычисления T определяются времена отказов каждого из N₀ образцов. В дальнейшем они в эксперименте не участвуют. Таким образом, среднее время безотказной работы характеризует надежность аппаратуры до первого отказа. Это означает, что T хорошо характеризует надежность аппаратуры разового использования, например, простейших элементов, которые после отказа не ремонтируются.

Величину T можно использовать и для оценки надежности сложных устройств. Однако в этом случае T характеризует надежность до первого их отказа.

У аппаратуры длительного использования, работающей в режиме смены отказавших элементов, среднее время безотказной работы до первого отказа может существенно отличаться от среднего времени между первым и вторым отказами, вторым и третьим и т.д. Это означает, что среднее время безотказной работы может характеризовать надежность такой аппаратуры только до первого отказа.

Поэтому надежность аппаратуры длительного использования оценивают, в отличие от среднего времени безотказной работы, так называемой наработкой на отказ.

Этой характеристике дают следующее определение: наработкой на отказ называется среднее значение времени между соседними отказами, при условии восстановления каждого отказавшего элемента.

Эта характеристика обозначается t_ср и определяется из статистических данных об отказах по формуле:

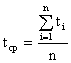, (1.27)

где t_i–время исправной работы аппаратуры между (i – 1)-м и i-м отказами; n – число отказов аппаратуры за время t.

Из определения и формулы (1.27) видно, что наработка на отказ является средним временем между соседними отказами. Формулой (1.27) удобно пользоваться, если t_ср определяется по данным об отказах лишь одного образца аппаратуры. Если испытание проводится с несколькими образцами, то t_ср вычисляется по формуле:

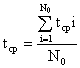(1.28)

где t_ср._i– среднее время между соседними отказами i-го образца, вычисленное по формуле (1.27), N₀–число испытываемых образцов.

Найти связь среднего времени между соседними отказами с другими количественными характеристиками надежности проще всего через среднюю частоту отказов. Действительно, если известны средние частоты отказов элементов сложной системы, то среднее число отказов системы в любом промежутке времени определяется ее суммарной частотой отказов. Тогда среднее время между соседними отказами будет равно величие, обратной суммарной частоте отказов, т.е.

(1.29)

или

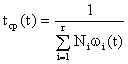, (1.30)

где r – число типов элементов.

Вероятность безотказной работы P(t), частота отказов α(t) (средняя частота отказов ), интенсивность отказов и среднее время безотказной работы T (среднее время между соседними отказами t_ср) являются основными количественными характеристиками надежности. Каждая из них имеет свои достоинства и недостатки. Ни одна из них не является исчерпывающей характеристикой надежности. Только все они в совокупности во многих случаях могут характеризовать достаточно полно надежность аппаратуры в течение времени ее работы.

Источник

Вероятность безотказной работы — это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает. Вероятность безотказной работы вместе с интенсивностью отказов определяет безотказность объекта (при этом вероятность безотказной работы обратна вероятности отказа объекта).

Показатель вероятности безотказной работы определяется статистической оценкой:
$P(t)={frac {N_{0}-n(t)}{N_{0}}}=1-{frac {n(t)}{N_{0}}}$
где $N_{0}$ — исходное число работоспособных объектов,
n(t) — число отказавших объектов за время .

Вероятность безотказной работы группы взаимосвязанных объектов равна произведению вероятностей безотказной работы каждого объекта в этой группе:
$P(t)=P_{1}(t)cdot P_{2}(t)cdot ...cdot P_{n}(t)=prod _{{k=1}}^{n}P_{k}(t)$
где n — число объектов в группе.

Чем больше объектов в группе, тем ниже надежность всей группы, так как если
$P_{1}(t)=P_{2}(t)=...=P_{n}(t)$ , то тогда
$P(t)=[P_{1}(t)]^{n}$ .

Среднее время безотказной работы системы[править | править код]

Среднее время безотказной работы (средняя наработка на отказ) $T_{0}$ — для невосстанавливаемых (неремонтируемых) систем — это математическое ожидание времени работы системы до отказа:

${displaystyle T_{0}=M=int limits _{0}^{mathcal {infty }}tcdot f(t)dt=-int limits _{0}^{mathcal {infty }}tdP(t)}$

Пределы несобственного интеграла изменяются от 0 до так как время не может быть отрицательным; f(t) — есть плотность вероятности возникновения отказов системы или её невосстанавливаемого элемента.

P(T) — есть вероятность безотказной работы в интервале времени В начальный момент вероятность P(T) равна единице. В конце времени работы системы вероятность P(T) равна нулю.

Вероятность P(T) связана с плотностью вероятности возникновения отказов системы или её невосстанавливаемого элемента следующим образом:

${displaystyle f(t)=-{frac {dP(t)}{dt}}.}$

Проинтегрировав выражение для $T_{0}$ по частям, получим:

${displaystyle T_{0}=int limits _{0}^{mathcal {infty }}P(t)dt.}$

Вероятность безотказной работы в зависимости от наработки

Графически полученное выражение для $T_{0}$ представлено на рисунке как площадь под графиком вероятности безотказной работы P(T) от времени В начальный момент вероятность </math>Р(T)</math> равна единице. В конце времени работы системы </math>P(T)</math> равна нулю.

Здесь Tgeq 0 — случайное время работы системы до отказа или наработка на отказ для невосстанавливаемого элемента или системы.

Типичные распределения времени безотказной работы[править | править код]

Основной источник: ^[1]

Экспоненциальное распределение: ${displaystyle f(t)=lambda e^{-lambda t}}$ , , .
Гамма-распределение: ${displaystyle f(t)={frac {lambda (lambda t)^{alpha -1}e^{-lambda t}}{Gamma (alpha )}}}$ , , .
Распределение Вейбулла: ${displaystyle f(t)=lambda alpha t^{alpha -1}e^{-lambda t^{alpha }}}$ , , .
Модифицированное распределение экстремального значения: ${displaystyle f(t)={frac {1}{lambda }}exp {left[-{frac {e^{t}-1}{lambda }}+tright]}}$ , , .
Усечённое нормальное распределение: ${displaystyle f(t)={frac {1}{asigma {sqrt {2pi }}}}exp {left[-{frac {(t-mu )^{2}}{2sigma ^{2}}}right]}}$ , , , .
Логарифмически-нормальное распределение: ${displaystyle f(t)={frac {1}{tsigma {sqrt {2pi }}}}exp {left[-{frac {(lg {t}-mu )^{2}}{2sigma ^{2}}}right]}}$ , , , .

Примечания[править | править код]

↑ Барлоу Р., Прошан Ф. Математическая теория надежности. -М.: Советское радио, 1969.- С. 29-30

Литература[править | править код]

Леликов О. П. Тема 2. Основные понятия и показатели надежности // Основы расчета и проектирования деталей и узлов машин. Конспект лекций по курсу “Детали машин”. — М.: Машиностроение, 2002. — С. 8-9. — 440 с. — 2000 экз. — ISBN 5-217-03077-1.

См. также[править | править код]

Расчёт надёжности
ГОСТ 27.002—89 (В викитеке)
Вероятность безотказной работы по ГОСТ 27.002-89

Источник

Оценка надежности системы и элементов требует введения количественных характеристик. Рассмотрим здесь некоторые из этих характеристик. Для краткости будем определять их применительно к «элементу»; однако те же определения будут относиться и к «системе».

Надежностью элемента (в узком смысле слова) называется вероятность того, что данный элемент в данных условиях будет работать безотказно в течение времени t. Эту вероятность мы будем обозначать Функция называется иногда «законом надежности».

Естественно, с увеличением времени функция убывает (рис. 7.1) При естественно предположить

Ненадежностью элемента называется вероятность того, что элемент откажет (выйдет из строя) в течение времени t. Очевидно,

Рассмотрим время Т безотказной работы элемента как случайную величину. Функция распределения этой случайной величины определяется как

Очевидно, — вероятность того, что за время t элемент откажет — представляет собой не что иное, как ненадежность элемента:

а его надежность дополняет до единицы:

Рис. 7.1

Рис. 7.2

Таким образом, ненадежность обладает свойствами функции распределения неотрицательной случайной величины. Она равна нулю при не убывает при возрастании t и стремится к единице при (рис. 7.2).

На практике обычно вместо функции распределения пользуются ее производной — плотностью распределения или плотностью вероятности:

График плотности показан на рис. 7.3. Площадь, ограниченная кривой равна единице.

Величина — элемент вероятности — истолковывается как вероятность того, что время Т примет значение, лежащее в пределах элементарного участка

В литературе по надежности функцию часто называют «плотностью отказов». Во избежание недоразумений, связанных с нечеткой терминологией, мы будем называть более точно: плотностью распределения времени безотказной работы.

Плотность может быть приближенно определена из опыта, для чего ставится следующий эксперимент: наблюдается работа большого числа N однородных элементов; каждый из них работает до момента отказа. Время, в течение которого работал элемент, регистрируется. Полученные значения времени:

обрабатываются обычными методами математической статистики: строится гистограмма (рис. 7.4) и выравнивается с помощью какой-нибудь плавной кривой, обладающей свойствами плотности.

Ордината гистограммы на каждом элементарном участке времени представляет собой не что иное, как среднее число отказов за единицу времени, приходящееся на один испытанный элемент. Тот же смысл можно приписать и функции Приближенно плотность определяется по формуле

где — число элементов, отказавших на участке времени от t до (время отсчитывается от момента включения); N — общее число элементов; — длина элементарного участка времени.

Рис. 7.3

Рис. 7.4

Пример. Было испытано ламп на длительность безотказной работы. Результаты испытаний приведены в табл. 2.1.

Таблица 2.1

Найти приближенно плотность для каждого участка времени, построить гистограмму и выровнять (от руки) плавной кривой. Решение. На первом участке (0—10 час) имеем:

на втором

и т. д. Значения плотности приведены в табл. 2.2.

Таблица 2.5

Гистограмма и выравнивающая кривая приведены на рис. 7.5. Отметим, что плотность изображенная на рис. 7.5, имеет максимум при т. е. максимальная частота отказов приходится на начальный период работы элемента.

Рис. 7.5

Такой характер кривой нередко наблюдается на практике, особенно при работе с электро- и радиодеталями, т. к. они часто имеют тенденцию отказывать немедленно или вскоре после включения. Иногда это повышение плотности в точке t=0 сказывается настолько резко, что заметную долю элементов можно считать отказавшими точно в момент включения. При этом время безотказной работы Т превращается из непрерывной в смешанную случайную величину, у которой одно значение обладает отличной от нуля вероятностью а для других существует только какая-то плотность распределения. Функция распределения такой случайной величины показана на рис. 7.6 — в точке она имеет скачок, равный а при — непрерывна.

Дифференцируя функцию при получим кривую «плотности» (рис. 7.7). Она характерна тем, что ограничивает площадь, равную уже не единице, а При обработке экспериментальных данных в таком случае отбирают в отдельную группу элементы, отказавшие при включении, и отношение их числа к общему числу N испытанных элементов считают за приближенное значение

а для остальных данных строится обычная гистограмма (при этом частоты находятся делением числа наблюдений в разряде на общее число наблюдений ).

В качестве характеристики надежности элемента часто применяется среднее время безотказной работы, т. е. математическое ожидание величины Т:

Рис. 7.6

Рис. 7.7

В случае, если величина Т непрерывна (т. е. ее функция распределения ) не имеет скачка при

Рис. 7.8

Рис. 7.9

В случае, когда Т — смешанная случайная величина, и отдельное значение имеет вероятность

Величина t может быть выражена не через плотность распределения а непосредственно через надежность . Действительно,

Интегрируя по частям, имеем:

Первый член в правой части выражения (2.9) равен нулю, так как для случайной величины Т, у которой существует математическое ожидание, разность при должна убывать быстрее, чем растет t. Поэтому

Эта формула имеет простую геометрическую интерпретацию: среднее время безотказной работы элемента равно полной площади S, ограниченной кривой надежности и осями координат (рис. 7.8).

Очевидно, в случае, когда Т — смешанная случайная величина (значение имеет вероятность ), это правило остается в силе; вся разница в том, что кривая будет начинаться не от 1, а от (рис. 7.9).