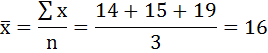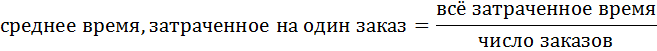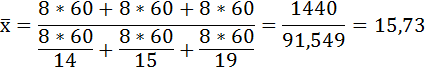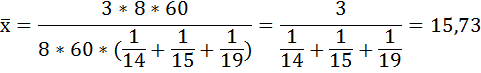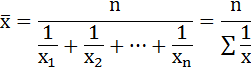Как найти среднее время обслуживания - Сайт, где вы сможете решить свои вопросы

В
теории
массового обслуживания время обслуживания,
т.е.
время пребывания одной заявки
в
канале
обслуживания считают
случайной величиной, распределенной,
как правило, по экспоненциальному закону
с плотностью
распределения (вероятностей)

(6.12)

Это обусловлено
многими причинами, среди которых следует
отметить: 1) отсутствие последействия;
2) достаточно корректное отражение
свойств многих реальных систем
обслуживания; 3) простоту и удобство
аналитических выражений.

Согласно
(6.12), среднее время обслуживания заявки
равно 1/
(ср. (6.9)). Величину 
называют
интенсивностью
обслуживания. Функция распределения
времени
обслуживания заявки равна

(6.13)

Ее
значение равно вероятности
того,
что к моменту времени t
обслуживание
заявки будет завершено, т.е. освободится
канал обслуживания.

Время
ожидания (время
пребывания заявки в очереди, если
последняя существует) также считают
случайной величиной, определенной, как
правило, по экспоненциальному закону
с точностью распределения (вероятностей)

(6.14)

и функцией
распределения

(6.15)

где v
—
величина, обратная среднему времени
ожидания, а значение H(t)
равно
вероятности того, что в момент t
начнется
обслуживание заявки.

Основные принципы
построения марковских моделей массового
обслуживания

1.
Процессы
массового обслуживания представляют
собой случайные
процессы с дискретными состояниями.
Переход
из одного возможного состояния в другое
происходит скачком в момент, когда
реализуется какое-то случайное
событие (поступление
новой заявки,
начало
или окончание обслуживания, уход заявки
из очереди
и
т.п.), вызывающее такой переход.

2. Для
процессов массового обслуживания с
простейшим
входным потоком и
экспоненциальным законом распределения
времени
обслуживания характерно
отсутствие последействия. Таким образом,
будущее развитие рассматриваемых
процессов зависит лишь от их текущих
состояний и не зависит от того, как
происходило их развитие в прошлом. А
это означает, что процессы массового
обслуживания с простейшим входным
потоком заявок и экспоненциальным
законом распределения времени обслуживания
являются марковскими
процессами с
дискретными
состояниями.

3. Предположим,
что в систему обслуживания с m
идентичными параллельными каналами
обслуживания поступает
простейший входной поток. При наличии
хотя бы одного свободного канала
немедленно начинается обслуживание
заявки, а
если все каналы заняты, то заявка
становится в очередь
(в системах
обслуживания с отказами заявка
покидает систему; в системах
обслуживания с ограниченной длиной
очереди заявка
становится в очередь, если там есть
свободное место, и покидает систему в
противном случае).

Пусть
S_i,
— возможное состояние рассматриваемой
системы обслуживания, характеризуемое
тем, что в ней занято ровно i
каналов
обслуживания, i
= 0…m,
а возможное состояние системы S_m₊_r
характеризуется тем, что все m
каналов обслуживания заняты и очередь
состоит из r
заявок, где r1.
Если на длину очереди не накладывают
ограничений, то r
может быть сколь угодно большим и
система может иметь счетное множество
состояний. Системы обслуживания с
отказами и с ограничениями на длину
очереди могут иметь лишь конечные
множества возможных состояний.

4. За
бесконечно малый промежуток времени
t
система обслуживания с простейшим
входным потоком заявок и экспоненциальным
законом распределения времени обслуживания
либо остается в прежнем состоянии (S),
либо переходит в соседнее (S_i₊₁
или S_i_-1при
i
1,
S₁
при
i=
0).

Таким
образом, в любой момент времени t
система
обслуживания с m
идентичными параллельными каналами
обслуживания находится в одном из
своих возможных состояний {S_i}ⁿ_i₌₀,
nN
или
п
=.
При этом:

если
i
= 0…m
, то занято i
каналов и очереди нет;

если
i
= m+1…n,
то заняты все m
каналов и в очереди находится (n
– m)
заявок;

если
n
= m,
то рассматривают систему обслуживания
с отказами;

если
m
< п
<
,
то рассматривают систему обслуживания
ограниченной длиной очереди;

если
п
=,
то рассматривают систему
обслуживания с ожиданием без
ограничений на длину очереди.

5. Пусть
{S_i}ⁿ_i₌₀—
множество возможных состояний
рассматриваемой системы обслуживания.
Для i
= 0,… п
введем
случайное
событие _i,-,
заключающееся в том, что в момент времени
t0
система находится в состоянии S_i,
и
обозначим вероятность
его
реализации через p_i(t):
Pi(t)
= P
[_i].
В
любой момент времени исходная система
может находиться лишь в одном из возможных
состояний, поэтому {_i}ⁿ_i₌₁—
полная группа событий и, как следствие,

(6.16)

Одна
из задач теории массового обслуживания
сводится к определению вероятностей
p_i(t),
i
= 0, ..n,
как функций времени.

6. Из
приведенных выше рассуждений и определения
марковского процесса с дискретными
состояниями следует, что рассматриваемые
процессы массового обслуживания являются
процессами
гибели —
размножения.
К
изложенному в 5.4 добавим следующее:

а)
элемент размеченного графа состояний
системы S,
соответствующий возможному состоянию
S_k,
будем
называть k-й
вершиной
графа; стрелки,
указывающие возможные переходы
системы S
из состояния в состояние, с записанными
переходными
вероятностями, —
нагруженными
дугами, а
переходные вероятности — весами]

б) при
составлении системы
уравнений Колмогорова можно
использовать следующее правило:
производная от вероятности пребывания
системы в состоянии S;
в момент времени t
равна
сумме произведений весов дуг, инцидентных
i-й
вершине размеченного графа состояний,
на вероятности
состояний, к
j
которым они направлены; при этом вес
дуги берется со знаком „плюс”, если
дуга направлена к i-й
вершине, соответствующей состоянию S_i,
и
со знаком „минус” в противном случае;

в)плотности
вероятностей переходов {_ij},
а
следовательно, и переходные вероятности
могут зависеть от структуры системы,
характеристик входного
потока и
параметров законов распределения
времени
ожидания и
времени
обслуживания.

>>>

Переход
из состояния S_i,
в „младшее” состояние S_i_-1
зависит лишь от освобождения каналов
обслуживания. Если .
—
интенсивность
обслуживания, то
функция
распределения времени
обслуживания определяется по формуле
(6.13). Поэтому

и, следовательно,

Таким
образом, при наличии лишь одного канала
обслуживания плотность вероятности
перехода в „младшее” состояние равна’
.
Если
занято i
каналов
и i
т
(т —
число каналов обслуживания), то в силу
независимости их функционирования
интенсивность обслуживания возрастает
в i
раз,
т.е.
_i,i-1=
i
.

>>>

Пример
6.2. Рассмотрим
простейшую задачу теории
массового обслуживания —
задачу о функционировании одноканальной
системы обслуживания с отказами, на
вход которой поступает простейший поток
заявок с интенсивностью
А
(заявка, заставшая канал занятым,
покидает систему), а время обслуживания
заявки — случайная величина, распределенная
по экспоненциальному закону с параметром

=
const.

В
данном случае система имеет лишь два
возможных состояния: s₀
—
канал свободен; S_i
— канал занят. Ее размеченный граф
состояний изображен на рис..

далее
(см. 6.5)
мы
докажем, что ₀₁
и ₁₀

.
Если
считать, что в начальный момент времени
t
= 0
система находилась в состоянии
s₀,
то
математическая
модель изучаемого
процесса массового обслуживания имеет
следующий вид:

При этом, учитывая,
что, согласно (6.16),

математическую
модель можно упростить:

Решив полученную
задачу Коши, находим (рис. 6.3)

Важнейшими
характеристиками системы обслуживания
с отказами являются:

а)
абсолютная
пропускная способность
—
среднее число заявок, которое может
обслужить система в единицу

времени;

б)
относительная
пропускная способность
—
отношение среднего числа заявок,
обслуживаемых системой в единицу
времени, к среднему числу поступивших
за это время заявок.

Нетрудно
убедиться в том, что в примере 6.2 функцию
p₀(t)
можно
интерпретировать как относительную
пропускную способность системы.
Действительно, p₀(t)
есть
вероятность того, что в момент t
канал
обслуживания свободен, т.е. что заявка,
поступившая в момент t,
будет обслужена. А это означает, что
p₀(t)
есть
отношение числа обслуженных заявок к
их общему числу, или относительная
пропускная способность системы.

При
стационарном
(установившемся)
режиме
функционирования имеем

(6.17)

Поэтому
в рассматриваемом случае относительная
пропускная способность системы
обслуживания равна 
/(
+ ,).
Можно
показать, что абсолютная пропускная
способность равна величине обратной
сумме среднего времени ожидания заявки
и среднего времени ее обслуживания:

(6.18)

Пример
6.3. Одноканальная
система обслуживания представляет
собой телефонную линию. Заявка-вызов,
поступившая в момент, когда линия
занята, получает отказ. Интенсивность
потока заявок 0,8 (вызовов в минуту).
Средняя продолжительность разговора
1,5 минуты. Считая поток заявок
простейшим, а время обслуживания
распределенным по экспоненциальному
закону, определим в стационарном режиме
функционирования:

1)
абсолютную пропускную способность
канала связи Q;

2)
относительную пропускную способность
канала связи q;

3)
вероятность отказа р_от.

Имеем

Таким образом,

Относительная
пропускная способность канала связи

есть вероятность
того, что заявка будет обслужена, не
получив

Отметим,
что номинальная пропускная способность
рассматриваемого канала связи Q_н_o_м,
являясь
величиной обратной по
отношению к средней продолжительности
времени разговора (Q_н_o_м
— 
= 2/3 =
0,66),
почти вдвое больше его пропускной
способности Q,
определенной с учетом случайного
характера потока заявок и времени
обслуживания.

Задания.

Моделирование
пуассоновского потока событий. Известно,
что распределение Пуассона есть
предельный случай биномиального
распределения при m

,
p0,
mp


, где p
–вероятность события при эксперименте,
m-
число экспериментов, 
– конечное число, называемое интенсивностью
потока.

Смоделируйте
случайный поток функцией
=ЕСЛИ(СЛЧИС()<$B$2;1;0) в столбик 50 – 100
значений (m)
, здесь в ячейке В2 находится вероятность
события (p);
задайте p
в пределах 0,02…0,2

Просчитайте
количество событий (k
) , т.е. найдите сумму по столбцу.
Распространите
вычисления на N
столбцов, (N>30),
найдите среднее значения для величины
k
и дисперсию данной величины, сравните
их с величиной =mp.
Проделайте
эксперимент, увеличивая m
до 100, N
до 50, уменьшая p,
сделайте выводы.

(Дисперсия и
математическое ожидание случайной
величины с распределения Пуассона равны
)

Проверьте
справедливость формулы 6.5 при больших
числах m
и N
на нескольких примерах.

Моделирование
функционирования одноканальной системы
массового обслуживания с отказами(см.
табл.)

	A	B	C	D	E	F
1		p(lam)		p(mu)
2		0,1		0,25
3		10		4
4	t	Zayavky		Zan do	Obsl	Zan pos
5

В столбце A
моделируется время начиная с шестой
строки (1, 2, 3…) будем условно считать,
что в минутах.

В ячейке B2
задается вероятность поступления
заявки, p(lam)=0,1
(1 заявка в 10 мин.,
=10).

В ячейке D2
задается интенсивность обслуживания.
p(mu)=
0,25 ( среднее время обслуживания одной
заявки при поступлении 4 мин, т.е. =4)

В столбце В, начиная
с В4, моделируется поток заявок с
параметром 
по средством функции =ЕСЛИ(СЛЧИС()<$B$2;1;0),
значение «1» соответствует поступлению
заявки.

В столбце D,
начиная с D4, (поле Zan
do)
определяется занятость канала на момент
до обслуживания на данном шаге (1-занят
, 0- свободен); в первом случае (ячейка
D6) это
зависит только от поступления заявки
( функция=ЕСЛИ(B6=1;1;0) ), на следующем шаге
и далее также от состояния занятости
на предыдущих шагах ( функция для D7
=ЕСЛИ(ИЛИ(B7=1;F6=1);1;0)).

В столбце E,
начиная с E4, моделируется поток
обслуживания с параметром ,
с учетом того, что обслуживание начинается
по поступлении заявки, т. е. канал
становится занятым, можно использовать
функцию для E6
=ЕСЛИ(D6=0;0; ЕСЛИ(СЛЧИС()<$D$2;1;0)); здесь
1-заявка обслужена, 0- пока не обслужена.

В столбце F,
начиная с F4, (поле Zan
pos)
определяется занятость канала на момент
после попытки обслуживания на данном
шаге (1-занят , 0- свободен); канал остается
занятым, если его не обслужили, т.е. можно
использовать следующую функцию для F6
=ЕСЛИ(И(D6=1;E6=0);1;0).

Последующие шаги
можно получить «потягиванием».

По имеющимся данным
для t=1,2…60.
найти

Общее число
поступивших заявок – n_Z(сумма по
столбцу B),
число обслуженных заявок – n_O(сумма
по столбцу D),
число потерянных заявок- n_P.
По формулам 6.17
найти вероятности p₀,
p₁обработки
(относительную
пропускную способность системы) и
потери заявки; проведя эксперимент
многократно 20-40 раз ( если активизировать
близлежащие ячейки результаты меняются)
найти средние для величин v₀=
n_O
/ n_Z_, v₁=
n_P
/ n_Z
и сравнить их с p₀,
p_1.
Найти абсолютную
пропускную способность системы по
формуле 6.18
и исходя из реальных данных как среднее
по разным экспериментам для величины
n_O
/ m,
где m
– наибольший отсчет времени ( в нашем
случае 60).

Изменяя 
и 
(соответственно p(lam)
и p(mu)
найдите характеристики работы системы,
сделайте выводы.

3) Попытайтесь
смоделировать двухканальную систему
массового обслуживания с отказами.
Поступающая заявка обслуживается
сначала первым каналом, при занятости
первого – вторым, при занятости обоих
каналов – теряется. Экспериментально
определите основные параметры при
разных параметрах ,
_1,
₂,
сделайте выводы. Что является более
эффективным: двухканальное обслуживание
с вероятностями обслуживания каналов
p(₁)
и p(₂)
или одноканальная с интенсивностью
обслуживания с вероятностью обслуживания
p()
= p(₁)
+p(₂)
?

Соседние файлы в папке Задания, лекции

#
#
#
#
#
#
#
#
#
#
02.05.201542.6 Кб47лаба.ods
#

Источник

СМО с ожиданием (очередью): определение и формулы

В качестве показателей эффективности СМО с ожиданием, кроме уже известных показателей — абсолютной и относительной пропускной способности, вероятности отказа $P_{text{otk}}$ , среднего числа занятых каналов к (для многоканальной системы) будем рассматривать также следующие:

1) $L_{text{sist.}}$ — среднее число заявок в системе;

2) $T_{text{sist.}}$ — среднее время пребывания заявки в системе;

3) $L_{text{och.}}$ — среднее число заявок в очереди (длина очереди);

4) $T_{text{och.}}$ — среднее время пребывания заявки в очереди;

5) $P_{text{zan.}}$ — вероятность того, что канал занят (степень загрузки канала).

Одноканальная система с неограниченной очередью

На практике часто встречаются одноканальные СМО с неограниченной очередью (например, телефон-автомат с одной будкой). Рассмотрим задачу.

Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность lambda , а поток обслуживании — интенсивность . Необходимо найти предельные вероятности состояний и показатели эффективности СМО.

Система может находиться в одном из состояний S_0,S_1,S_2,ldots,S_k , по числу заявок, находящихся в СМО: S_0 — канал свободен; S_1 — канал занят (обслуживает заявку), очереди нет; S_2 — канал занят, одна заявка стоит в очереди; — канал занят, (k-1) заявок стоят в очереди и т.д.

Граф состояний СМО представлен на рис. 8.

Граф состояний одноканальной СМО с неограниченной очередью

Это процесс гибели и размножения, но с бесконечным числом состояний, в котором интенсивность потока заявок равна lambda , а интенсивность потока обслуживании .

Прежде чем записать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время ttoinfty , очередь может неограниченно возрастать. Доказано, что если rho<1 , т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если rhogeqslant1 , очередь растет до бесконечности.

Для определения предельных вероятностей состояний воспользуемся формулами (16), (17) для процесса гибели и размножения (здесь мы допускаем известную нестрогость, так как ранее эти формулы были получены для случая конечного числа состояний системы). Получим:

$p_0=left[1+ frac{lambda}{mu}+ left(frac{lambda}{mu}right)^{2}+ldots+ left(frac{lambda}{mu}right)^{k}+ldotsright]^{-1}= left(1+rho+rho^2+ldots+rho^k+ldotsright)^{-1}.$

(32)

Так как предельные вероятности существуют лишь при rho<1 , то геометрический ряд со знаменателем rho<1 , записанный в скобках в формуле (32), сходится к сумме, равной $frac{1}{1-rho}$ . Поэтому

p_0=1-rho,

(33}

и с учетом соотношений (17)

p_1=rhocdot p_0,quad p_2=rho^2cdot p_0,quadldots,quad p_k=rho^kcdot p_0,quadldots

найдем предельные вероятности других состояний

p_1=rho(1-rho),quad p_2=rho^2(1-rho),quadldots,quad p_k=rho^k(1-rho),quad ldots

(34)

Предельные вероятности p_0,p_1,p_2,ldots,p_k,ldots образуют убывающую геометрическую профессию со знаменателем rho<1 , следовательно, вероятность p_0 — наибольшая. Это означает, что если СМО справляется с потоком заявок (при rho<1 ), то наиболее вероятным будет отсутствие заявок в системе.

Среднее число заявок в системе $L_{text{sist.}}$ определим по формуле математического ожидания, которая с учетом (34) примет вид

$L_{text{sist.}}= sum_{k=1}^{infty}kp_k=(1-rho)sum_{k=1}^{infty}krho^k$

(35)

(суммирование от 1 до infty , так как нулевой член 0cdot p_0=0 ).

Можно показать, что формула (35) преобразуется (при rho<1 ) к виду

$L_{text{sist.}}=frac{rho}{1-rho},.$

(36)

Найдем среднее число заявок в очереди $L_{text{och.}}$ . Очевидно, что

$L_{text{och.}}= L_{text{sist.}}- L_{text{ob.}},$

(37)

где $L_{text{ob.}}$ — среднее число заявок, находящихся под обслуживанием.

Среднее число заявок под обслуживанием определим по формуле математического ожидания числа заявок под обслуживанием, принимающего значения 0 (если канал свободен) либо 1 (если канал занят):

$L_{text{ob.}}=0cdot p_0+1cdot (1-p_0),$

т.е. среднее число заявок под обслуживанием равно вероятности того, что канал занят:

$L_{text{ob.}}=P_{text{zan.}}=1-p_0.$

(38)

В силу (33)

$L_{text{ob.}}=P_{text{zan.}}=rho.$

(39)

Теперь по формуле (37) с учетом (36) и (39)

$L_{text{och.}}=frac{rho^2}{1-rho},.$

(40)

Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (в очереди), деленному на интенсивность потока заявок, т.е.

$T_{text{sist.}}=frac{1}{lambda}cdot L_{text{sist.}} ,$

(41)

$T_{text{och.}}=frac{1}{lambda}cdot L_{text{och.}}.$

(42)

формулы (41) и (42) называются формулами Литтла. Они вытекают из того, что в предельном, стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих ее: оба потока заявок имеют одну и ту же интенсивность lambda .

На основании формул (41) и (42) с учетом (36) и (40) среднее время пребывания заявки в системе определится по формуле:

$T_{text{sist.}}=frac{rho}{lambda(1-rho)},,$

(43)

а среднее время пребывания заявки в очереди —

$T_{text{och.}}=frac{rho^2}{lambda(1-rho)},.$

(44)

Пример 8. В порту имеется один причал для разгрузки судов. Интенсивность потока судов равна 0,4 (судов в сутки). Среднее время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.

Решение. Имеем $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}=0,!4cdot2=0,!8$ . Так как rho=0,!8<1 , то очередь на разгрузку не может бесконечно возрастать и предельные вероятности существуют. Найдем их.

Вероятность того, что причал свободен, по (33) p_0=1-0,!8=0,!2 , а вероятность того, что он занят, $P_{text{zan.}}=1-0,!2=0,!8$ . По формуле (34) вероятности того, что у причала находятся 1, 2, 3 судна (т.е. ожидают разгрузки 0, 1, 2 судна), равны

p_1=0,!8(1-0,!8)=0,!16;quad p_2=0,!8^2(1-0,!8)=0,!128;quad p_3=0,!8^3(1-0,!8)=0,!1024.

Вероятность того, что ожидают разгрузку не более чем 2 судна, равна

P=p_1+p_2+p_3=0,!16+0,!128+0,!1024=0,!3904.

По формуле (40) среднее число судов, ожидающих разгрузки, $L_{text{och.}}=frac{0,!8^2}{1-0,!8}=3,!2$ среднее время ожидания разгрузки по формуле (42) $T_{text{och.}}=frac{3,!2}{0,!8}=4$ (сутки).

По формуле (36) среднее число судов, находящихся у причала, $L_{text{sist.}}=frac{0,!8}{1-0,!8}=4$ (сутки) (или проще по (37) $L_{text{sist.}}=3,!2+0,!8=4$ (сутки), а среднее время пребывания судна у причала по формуле (41) $T_{text{sist.}}=frac{4}{0,!8}=5$ (сутки).

Очевидно, что эффективность разгрузки судов невысокая. Для ее повышения необходимо уменьшение среднего времени разгрузки судна $overline{t}_{text{ob.}}$ либо увеличение числа причалов.

Многоканальная СМО с неограниченной очередью

Рассмотрим задачу. Имеется n-канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность lambda , а поток обслуживании — интенсивность . Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.

Система может находиться в одном из состояний S_0,S_1,S_2,ldots,S_k,ldots,S_n,ldots нумеруемых по числу заявок, находящихся в СМО: S_0 — в системе нет заявок (все каналы свободны); S_1 — занят один канал, остальные свободны; S_2 — заняты два канала, остальные свободны; ldots,S_k — занято каналов, остальные свободны; ldots,S_n — заняты все каналов (очереди нет); $S_{n+1}$ — заняты все каналов, в очереди одна заявка; $ldots,S_{n+r}$ — заняты все каналов, заявок стоит в очереди, и т.д.

Граф состояний системы показан на рис. 9. Обратим внимание на то, что в отличие от предыдущей СМО, интенсивность потока обслуживании (переводящего систему из одного состояния в другое справа налево) не остается постоянной, а по мере увеличения числа заявок в СМО от 0 до увеличивается от величины до nmu , так как соответственно увеличивается число каналов обслуживания. При числе заявок в СМО большем, чем , интенсивность потока обслуживании сохраняется равной nmu .

Граф состояний многоканальной СМО с неограниченной очередью

Можно показать, что при $frac{rho}{n}<1$ предельные вероятности существуют. Если $frac{rho}{n}geqslant1$ , очередь растет до бесконечности. Используя формулы (16) и (17) для процесса гибели и размножения, можно получить следующие формулы для предельных вероятностей состояний n-канальной СМО с неограниченной очередью

$p_0={left(1+ frac{rho^1}{1!}+ frac{rho^2}{2!}+ldots+frac{rho^n}{n!}+ frac{rho^{n+1}}{n!(n-rho)}right)!}^{-1},$

(45)

$p_1=frac{rho^1}{1!}cdot p_0,~ldots,~ p_k=frac{rho^k}{k!}cdot p_0,~ldots,~ p_n=frac{rho^n}{n!}cdot p_0,$

(46)

$p_{n+1}=frac{rho^{n+1}}{ncdot n!}cdot p_0,~ldots,~p_{n+r}=frac{rho^{n+r}}{n^rcdot n!}cdot p_0,~ldots$

(47)

Вероятность того, что заявка окажется в очереди,

$P_{text{och.}}=frac{rho^{n+1}}{n!(n-rho)}cdot p_0.$

(48)

Для n-канальной СМО с неограниченной очередью, используя прежние приемы, можно найти:

среднее число занятых каналов

$overline{k}=frac{lambda}{mu}=rho,$

(49)

среднее число заявок в очереди

$L_{text{och.}}=frac{rho^{n+1}cdot p_0}{ncdot n!}cdotleft(1-frac{rho}{n}right)^{-2},,$

(50)

среднее число заявок в системе

$L_{text{sist}}=L_{text{och.}}+rho.$

Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе, как и ранее, находятся по формулам Литтла (42) и (41).

Замечание. Для СМО с неограниченной очередью при rho<1 любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа $P_{text{otk.}}=0$ , относительная пропускная способность Q=1 , а абсолютная пропускная способность равна интенсивности входящего потока заявок, т.е. A=lambda .

Пример 9. В универсаме к узлу расчета поступает поток покупателей с интенсивностью lambda=81 чел. в час. Средняя продолжительность обслуживания контролером-кассиром одного покупателя $overline{t}_{text{ob.}}=2$ мин. Определить:

а. Минимальное количество контролеров-кассиров $n_{min}$ , при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при $n=n_{min}$ .

б. Оптимальное количество $n_{text{opt.}}$ контролеров-кассиров, при котором относительная величина затрат $C_{text{otn.}}$ , связанная с издержками на содержание каналов обслуживания и с пребыванием в очереди покупателей, задаваемая, например, как $C_{text{otn.}}=frac{n}{lambda}+3T_{text{och.}}$ , будет минимальна, и сравнить характеристики обслуживания при $n=n_{min}$ и $n=n_{text{opt.}}$ .

в. Вероятность того, что в очереди будет не более трех покупателей.

Решение. а. По условию lambda=81 (1/ч) $=frac{81}{60}=1,!35$ (1/мин.). По формуле (24) $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}=1,!35cdot2=2,!7$ . Очередь не будет возрастать до бесконечности при условии $frac{rho}{n}<1$ , т.е. при n>rho=2,!7 . Таким образом, минимальное количество контролеров-кассиров $n_{min}=3$ .

Найдем характеристики обслуживания СМО при n=3 .

Вероятность того, что в узле расчета отсутствуют покупатели, по формуле (45)

$p_0={left(1+2,!7+ frac{2,!7^2}{2!}+ frac{2,!7^3}{3!}+ frac{2,!7^4}{3!(3-2,!7)}right)!}^{-1}=0,!025$

т.е. в среднем 2,5% времени контролеры-кассиры будут простаивать.

Вероятность того, что в узле расчета будет очередь, по (48)

$P_{text{och.}}=frac{2,!7^4}{3!cdot(3-2,!7)}cdot0,!025=0,!735.$

Среднее число покупателей, находящихся в очереди, по (50)

$L_{text{och.}}=frac{2,!7^4}{3cdot3!cdot(1-2,!7/3)^2}cdot0,!025=7,!35.$

Среднее время ожидания в очереди по (42)

$T_{text{och.}}=frac{7,!35}{1,!35}=5,!44$ (мин).

Среднее число покупателей в узле расчета по (51)

$L_{text{sist.}}= 7,!35+2,!7=10,!05.$

Среднее время нахождения покупателей в узле расчета по (41)

$T_{text{sist.}}=frac{10,!05}{1,!35}approx7,!44$ (мин).

Среднее число контролеров-кассиров, занятых обслуживанием покупателей, по (49) overline{k}=2,!7 .

Коэффициент (доля) занятых обслуживанием контролеров-кассиров $overline{k}_{text{otn.}}=frac{rho}{n}=frac{2,!7}{3}=0,!9$ .

Абсолютная пропускная способность узла расчета A=1,!35 (1/мин), или 81 (1/ч), т.е. 81 покупатель в час.

Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех контролеров-кассиров.

б. Относительная величина затрат при n=3

$C_{text{otn.}}=frac{n}{lambda}+3T_{text{och.}}=frac{3}{1,!35}+3cdot5,!44=5,!44.$

Рассчитаем относительную величину затрат при других значениях (табл. 2).

Расчёт относительных величин затрат

Как видно из табл. 2, минимальные затраты получены при $n=n_{text{opt.}}=5$ контролерах-кассирах.

Определим характеристики обслуживания узла расчета при $n=n_{text{opt.}}=5$ . Получим

$P_{text{och.}}=0,!091;~ L_{text{och.}}= 0,!198;~ T_{text{och.}}=0,!146;~ L_{text{sist.}}=2,!9;~ T_{text{sist.}}=2,!15;~ overline{k}=2,!7;~k_3=0,!54.$

Как видим, при n=5 по сравнению с n=3 существенно уменьшились вероятность возникновения очереди $P_{text{och.}}$ , длина очереди $L_{text{och.}}$ и среднее время пребывания в очереди $T_{text{och.}}$ , и соответственно среднее число покупателей $L_{text{sist.}}$ и среднее время нахождения в узле расчета $T_{text{sist.}}$ , а также доля занятых обслуживанием контролеров k_3 . Но среднее число занятых обслуживанием контролеров-кассиров overline{k} и абсолютная пропускная способность узла расчета естественно не изменились.

в. Вероятность того, что в очереди будет не более 3 покупателей, определится как

$P{rleqslant3}=p_1+p_2+p_3+p_4+p_5+p_{5+1}+p_{5+2}+p_{5+3}=1-P_{text{och.}}+p_{5+1}+p_{5+2}+p_{5+3},$

где каждое слагаемое найдем по формулам (45)–(48). Получим при n=5:

$P{rleqslant3}=1-frac{2,!7^6}{5!(5-2,!3)}cdot 0,!065+frac{2,!7^6}{5cdot5!}cdot0,!065 +frac{2,!7^7}{5^2cdot5!}cdot0,!065 +frac{2,!7^8}{5^3cdot5!}cdot0,!065=0,!986.$

(Заметим, что в случае n=3 контролеров-кассиров та же вероятность существенно меньше: P{rleqslant3}=0,!464 ).

Пример 10. Железнодорожная касса с двумя окошками продает билеты в два пункта и . Интенсивность потока пассажиров, желающих купить билеты, для обоих пунктов одинакова: $lambda_{A}=lambda_{B}=0,!45$ (пассажиров в минуту). На обслуживание пассажиров кассир тратит в среднем 2 мин. Рассматриваются два варианта продажи билетов: первый — билеты продаются в одной кассе с двумя окошками одновременно в оба пункта и , второй — билеты продаются в двух специализированных кассах (по одному окошку в каждой), одна только в пункт , другая — только в пункт . Необходимо:

а. Сравнить два варианта продажи билетов по основным характеристикам обслуживания.

б. Определить, как надо изменить среднее время обслуживания одного пассажира, чтобы по второму варианту продажи пассажиры затрачивали на приобретение билетов в среднем меньше времени, чем по первому варианту.

Решение.
а. По первому варианту имеем двухканальную СМО, на которую поступает поток заявок интенсивностью lambda=0,!45+0,!45=0,!9 ; интенсивность потока обслуживании $mu=frac{1}{2}=0,!5;$ $rho=frac{lambda}{mu}=1,!8$ . Так как $frac{rho}{n}=frac{1,!8}{2}=0,!9<1$ , то предельные вероятности существуют.

Вероятность простоя двух кассиров по (45)

$p_0={left(1+ frac{1,!8}{1!}+ frac{1,!8^2}{2!}+ frac{1,!8^3}{2!cdot(2-1,!8)}right)!}^{-1}approx0,!0526.$

Среднее число пассажиров в очереди по (50)

$L_{text{och.}}=frac{1,!8^3}{2cdot2!cdot(1-1,!8/2)^2}cdot0,!0526=7,!67.$

Среднее число пассажиров у кассы по (51)

$L_{text{sist.}}= 7,!67+1,!8=9,!47.$

Среднее время на ожидание в очереди и покупку билетов равно соответственно (по формулам (42) и (41)):

$T_{text{och.}}=frac{7,!67}{0,!9}=8,!52$ (мин) и $T_{text{sist.}}=frac{9,!47}{0,!9}=10,!5$ (мин).

По второму варианту имеем две одноканальные СМО (два специализированных окошка); на каждую поступает поток заявок с интенсивностью lambda=0,!45 . По-прежнему mu=0,!5; $rho=frac{lambda}{mu}=0,!9<1$ , предельные вероятности существуют. По формулам (40), (36), (42), (41)

$L_{text{och.}}=frac{0,!9^2}{1-0,!9}=8,!1;~ L_{text{sist.}}=frac{0,!9}{1-0,!9}=9;~ T_{text{och.}}=frac{8,!1}{0,!45}=18;~ T_{text{sist.}}=frac{9}{0,!45}=20.$

Итак, по второму варианту увеличились и длина очереди, и среднее время ожидания в ней и в целом на покупку билетов. Такое различие объясняется тем, что в первом варианте (двухканальная СМО) меньше средняя доля времени, которую простаивает каждый из двух кассиров: если он не занят обслуживанием пассажира, покупающего билет в пункт , он может заняться обслуживанием пассажира, покупающего билет в пункт , и наоборот. Во втором варианте такой взаимозаменяемости нет.

Можно заметить, что среднее время на покупку билетов по второму варианту увеличилось более чем в 2 раза. Такое значительное увеличение связано с тем, что СМО работает на пределе своих возможностей (rho=0,!9) : достаточно незначительно увеличить среднее время обслуживания $overline{t}_{text{ob.}}$ , т.е. уменьшить , и rho превзойдет 1, т.е. очередь начнет неограниченно возрастать.

б. Выше было получено, что по первому варианту продажи билетов при среднем времени обслуживания одного пассажира $overline{t}_{text{ob.}}=2$ (мин) среднее время на покупку билетов составит $T_{text{sist.1}}=10,!5$ (мин). По условию для второго варианта продажи $T_{text{sist.2}}<T_{text{sist.1}}$ , или с учетом (36) и (41): $frac{1}{lambda}frac{rho}{1-rho}< T_{text{sist.1}}$ .

Полагая $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}$ , получим $-frac{overline{t}_{text{ob.}}}{1-lambdaoverline{t}_{text{ob.}}}<T_{text{sist.1}}$ , откуда найдем $overline{t}_{text{ob.}}<frac{T_{text{sist.1}}}{1+lambda T_{text{sist.1}}}$ или $overline{t}_{text{ob.}}<frac{10,!5}{1+0,!45cdot10,!5}=1,!83$ (мин).

Итак, средние затраты времени на покупку билетов по второму варианту продажи уменьшатся, если среднее время обслуживания одного пассажира уменьшится более чем на 0,17 мин, или более чем на 8,5%.

СМО с ограниченной очередью

СМО с ограниченной очередью отличаются от рассмотренных выше задач лишь тем, что число заявок в очереди ограничено (не может превосходить некоторого заданного ). Если новая заявка поступает в момент, когда все места в очереди заняты, она покидает СМО необслуженной, т.е. получает отказ.

Очевидно: для вычисления предельных вероятностей состояний и показателей эффективности таких СМО может быть использован тот же подход, что и выше, с той разницей, что суммировать надо не бесконечную прогрессию (как, например, мы делали при выводе формулы (33)), а конечную. Соответствующие формулы сведем в табл. 3.

Среднее время пребывания заявки в очереди и в системе, как и ранее, определяем по формулам Литтла (44) и (43).

Таблица 3. Показатели одно- и многоканальной СМО с ограниченной очередью

Показатели одно- и многоканальной СМО с ограниченной очередью

Пример 11. По условию примера 8 найти показатели эффективности работы причала. Известно, что приходящее судно покидает причал (без разгрузки), если в очереди на разгрузку стоит более 3 судов.

Решение. По условию m=3 . Используем формулы, приведенные во второй графе табл. 3.

Вероятность того, что причал свободен:

$p_0=frac{1-0,!6}{1-0,!8^{3+2}}=0,!297.$

Вероятность того, что приходящее судно покинет причал без разгрузки:

$P_{text{otk.}}=0,!8^{3+1}cdot 0,!122.$

Относительная пропускная способность причала:

Q=1-0,!122=0,!878.

Абсолютная пропускная способность причала A=0,!4cdot0,!878=0,!351 , т.е. в среднем в сутки разгружается 0,35 судна.

Среднее число судов, ожидающих разгрузку

$L_{text{och.}}=frac{0,!8^2cdot[1-0,!8^3cdot(3+1-3cdot0,!8)]}{(1-0,!8^{3+2})(1-0,!8)}=0,!861,$

а среднее время ожидания разгрузки по (42)

$T_{text{och.}}=frac{0,!861}{0,!8}=1,!076$ (сутки).

Среднее число судов, находящихся у причала $L_{text{sist.}}=0,!861+(1-0,!297)=1,!564$ , а среднее время пребывания судна у причала по (41):

$T_{text{sist.}}=frac{1,!564}{0,!8}=1,!955$ (сутки).

СМО с ограниченным временем ожидания

На практике часто встречаются СМО с так называемыми “нетерпеливыми” заявками. Такие заявки могут уйти из очереди, если время ожидания превышает некоторую величину. В частности, такого рода заявки возникают в различных технологических системах, в которых задержка с началом обслуживания может привести к потере качества продукции, в системах оперативного управления, когда срочные сообщения теряют ценность (или даже смысл), если они не поступают на обслуживание в течение определенного времени.

В простейших математических моделях таких систем предполагается, что заявка может находиться в очереди случайное время, распределенное по показательному закону с некоторым параметром , т.е. можно условно считать, что каждая заявка, стоящая в очереди на обслуживание, может покинуть систему с интенсивностью .

Соответствующие показатели эффективности СМО с ограниченным временем получаются на базе результатов, полученных для процесса гибели и размножения.

В заключение отметим, что на практике часто встречаются замкнутые системы обслуживания, у которых входящий поток заявок существенным образом зависит от состояния самой СМО. В качестве примера можно привести ситуацию, когда на ремонтную базу поступают с мест эксплуатации некоторые машины: понятно, что чем больше машин находится в состоянии ремонта, тем меньше их продолжает эксплуатироваться и тем меньше интенсивность потока вновь поступающих на ремонт машин. Для замкнутых СМО характерным является ограниченное число источников заявок, причем каждый источник “блокируется” на время обслуживания его заявки (т.е. он не выдает новых заявок). В подобных системах при конечном числе состояний СМО предельные вероятности будут существовать при любых значениях интенсивностей потоков заявок и обслуживании. Они могут быть вычислены, если вновь обратиться к процессу гибели и размножения.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

В отделе заказов торговой фирмы занято трое работников, имеющих 8-часовой рабочий день. Первый работник на оформление одного заказа в среднем затрачивает 14 мин., второй – 15, третий – 19 мин. Определите средние затраты времени на 1 заказ в целом по отделу.

Решение:

На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:

Полученная средняя была бы правильной, если бы каждый работник отдела оформил только один заказ. Но в течение дня отдельными работниками было оформлено различное число заказов. Для определения числа заказов, оформленных каждым работником, воспользуемся следующим соотношением:

Число заказов, оформленных каждым работником, определяется отношением всего времени работы к среднему времени, затраченному на один заказ. Тогда среднее время, необходимое для оформления одного заказа, равно: