Как найти среднее время в физике формула

• Комментировать
• Жалоба
• Ссылка

План урока:

Среднее значение

Скорость. Время. Расстояние

Взаимосвязь между скоростью, временем и расстоянием

Задачи на движение

На уроке узнаем, что означает «среднее арифметическое» и как его находят, будем решать задачи с величинами «скорость», «время», «расстояние».

Начнем урок с небольшой тренировки ума! Игра называется «Тройка». Вам нужно собрать в левой части три слагаемых так, чтобы получилось число за красной чертой. Считайте устно. Образец дан в первой строке: 18 + 34 + 16 = 68

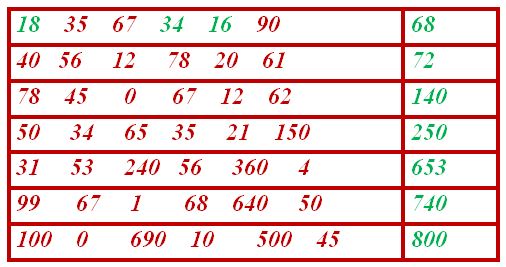
Проверь себя.

40 + 20 + 12 = 72

78 + 0 + 62 = 140

65 + 35 + 150 = 250

53 + 240 +360 = 653

99 + 1 + 640 = 740

690 + 10 + 100 = 800

Среднее значение

Каждый из нас в жизни встречается с выражениями «в среднем», «средняя температура», «средний заработок». Что это значит?

Рассмотрим на конкретной задаче.

Три друга Иван, Костя и Владимир каждую среду идут вместе от школы до музыкальной студии, где учатся игре на гитаре. Иван от школы до студии насчитал 251 шаг. Костя – 248 шагов, а Владимир насчитал 254 шага. Сколько в среднем шагов от школы до музыкальной студии?

В математике существует понятие «среднее арифметическое». Чтобы найти среднее арифметическое в этой задаче, нужно сложить количество шагов трех друзей, а затем полученную сумму разделить на 3 (по количеству слагаемых).

251 + 248 + 254 = 753 шага.

753 : 3 = 251 шаг

Можно сказать, что от школы до музыкальной студии в среднем 251 шаг.

Составим алгоритм.

Например, найти среднее арифметическое чисел: 5, 8, 7, 4.

Находим сумму чисел 5 + 8 + 7 + 4 = 24

Количество слагаемых – 4, значит, полученную сумму разделим на 4.

24 : 4 = 6

Среднее арифметическое – 6.

Пользуясь алгоритмом, найдите среднее арифметическое чисел: 12, 10, 8.

Проверь себя.

12 + 10 + 8 = 30

30 : 3 = 10

Среднее арифметическое – 10.

Рассмотрим более сложную задачу на нахождение среднего арифметического.

Задача

В столовой детского сада для приготовления завтраков малышам расходовали молоко три дня по 20 л и два дня по 25 л. Сколько в среднем расходовали молока в день?

Решим задачу вместе.

Сначала узнаем, сколько всего молока израсходовали.

20 ∙ 3 + 25 ∙ 2 = 110 (л) – израсходовали всего.

Затем узнаем, сколько дней расходовали молоко на завтрак.

3 + 2 = 5(дн.) – расходовали молоко.

Осталось количество израсходованного молока разделить на число дней.

110 : 5 = 22 (л) – расходовали в среднем за день.

Попробуйте самостоятельно решить подобную задачу.

Задача

Для игрового уголка в классе родители закупили 3 настольные игры: «Пазлы», «Домино», «Математический тренажер». Игра «Пазлы» стоила 160 р., «Домино» – 210 р., а «Математический тренажер» – 230 р.. Найди среднюю стоимость настольной игры.

Проверь себя.

• 160 + 210 + 230 = 600 (р.) – заплатили за все игры.
• 600 : 3 = 200 (р.) – стоит в среднем одна настольная игра.
• Ответ: 200 рублей

Скорость. Время. Расстояние

Скорость

Вы наблюдали, что вокруг нас постоянно что-то или кто-то движется. Некоторые объекты – быстро, а некоторые – совсем медленно. Например, по лесной тропе прогуливается человек, по шоссе едет автомобиль, по воздуху летит вертолет. Все они движутся. Но автомобиль движется быстрее, чем человек, а вертолет – быстрее автомобиля.

В математике, величиной характеризующей быстроту движения объектов называют скоростью.

Скорость движения – это расстояние, пройденное за единицу времени. Единицей времени может быть:  1 секунда, 1 минута, 1 час.

Давайте вместе разберем две простые задачи.

Легковая машина прошла 120 км за 2 часа. В течение каждого часа она проходила одинаковое расстояние. Сколько км прошла машина за 1 час?

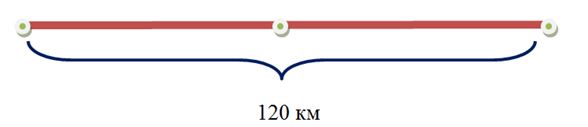
120 : 2 = 60 (км) – пройдет машина за 1 час.

Таким образом, скорость движения машины 60 км в час. Сокращенно запишем так:

60 км/ч.

Космический корабль пролетает 8 000 м за 1 секунду. Как по-другому записать его скорость?

Его скорость можно записать так: 8 000 м/с. Мы знаем, что 1 км = 1000 м, поэтому скорость корабля можно записать по-другому: 8 км/с.

Посмотрите скорость движения некоторых  животных. Какое животное самое медленное, самое быстрое? Обратите внимание, что скорость можно записать по-разному: в зависимости от того, сколько сантиметров, метров, километров кто-то пролетает, проползает или пробегает за секунду, минуту, час.

Время

С единицами времени вы уже знакомы. Это: секунда, минута, час, сутки, неделя, месяц, год, век.

Расстояние

Расстояние – это длина дороги, соединяющая начало и конец пути.

Расстояние измеряется в следующих единицах:

Миллиметр

Сантиметр

Дециметр

Метр

Километр

Взаимосвязь между скоростью, временем и расстоянием

Как же связаны между собой эти величины?

Давайте запомним условные обозначения, принятые в математике:

Скорость – v,

Время – t,

Расстояние – S.

Ребята, это три ключевых формулы для решения задач на движение, которые нужно знать назубок!

Задачи на движение

С задачами на движение мы встречаемся каждый день в обычной жизни.

Расстояние – самое большое из трех величин в задачах на движение. То есть, скорость и время всегда меньше расстояния.

Запомнили формулы, которые являются ключами к правильному решению задач?

Заполните пустые окошки в формулах:

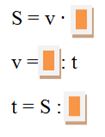
Решим задачи на движение.

Плот двигался по реке со скоростью 5 км/ч, а катер – со скоростью 20 км/ч. Какое расстояние преодолеет плот, и какое катер за 3 часа?

Выделяем величины, чертим таблицу. Читаем задачу по частям и записываем каждую величину в нужную ячейку таблицы.

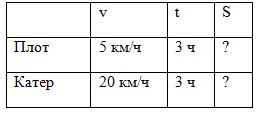
Какую из трех величин нужно найти? Верно, расстояние. Вспомним формулу: S = v ∙ t

5 ∙ 3 + 15 (км) – пройдет плот.

20 ∙ 3 = 60 (км) – пройдет катер.

Ответ: 15 км, 60 км.

Ребята участвовали в соревнованиях по бегу. Максим пробежал 200 м за 40 с, а Артем это же расстояние пробежал за 50 с. С какой скоростью бежал каждый из мальчиков?

Начертите  таблицу, как в предыдущей задаче. Запишите величины в нужные ячейки. Поставьте знак вопроса. Пользуясь формулой, решите задачу самостоятельно.

Проверь себя.

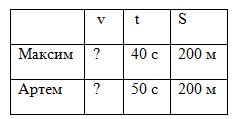
v = S : t

200 : 40 = 5 (м/с) – скорость движения Максима.

200 : 5 = 4 (м/с) – скорость движения Артема.

Ответ: 5 м/с, 4 м/с.

Решим еще одну задачу.

Два всадника отправились на прогулку на лошадях Рада и Снежка. Лошади преодолели одинаковое расстояние 30 км. Но двигались с разной скоростью. Рада бежала со скоростью 10 км/ч, а Снежка – 15 км/ч. Сколько времени длилась прогулка на Раде, и сколько времени – на Снежке?

Начертите таблицу, заполните ее ячейки. Пользуясь формулой, запишите решение.

Проверь себя.

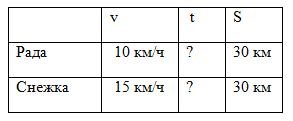
t = S : v

30 : 10 = 3 (ч) – прогулка на Раде.

30 : 15 = 2 (ч) – прогулка на Снежке.

Ответ: 3 ч, 2 ч.

Сегодня на уроке мы запомнили формулы-ключи для решения задач на движение, узнали о скорости самых медленных и самых быстрых животных, научились находить среднее арифметическое. До скорых встреч, ребята!

Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.

1. Половина пути

Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?

Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.

Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.

Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.

Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.

Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.

Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.

Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.

Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.

Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.

2. Средняя скорость по графику пути

Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.

По графику видно, что движение состоит из четырех этапов:

1. Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
2. Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
3. Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
4. Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.

Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!

Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.

3. Средняя скорость по графику скорости

Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.

Читаем график. Движение состоит из трёх этапов

1. С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
2. От 2 до 6 с тело движется со скоростью 6 м/с
3. В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.

Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.

Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.

Общие рекомендации для решения задач на среднюю скорость

1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.

2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.

3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.

Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!

Как найти среднее значение чисел?

Среднее значение Это арифметическое и вычисляется путем с добавления группы чисел и деления на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6. Медиана Среднее число числа.

Что такое среднее значение в физике?

В теории вероятностей и статистике

среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.

Как рассчитать среднее значение между двумя числами?

Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.

Как рассчитать среднее значение в Excel?

Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула.

Как найти среднее значение за месяц?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

1. x – среднее арифметическое;
2. xn – конкретное значение;
3. n – количество значений .

Как найти среднее значение в ворде?

Чтобы вычислить среднее арифметическое в строке или столбце, ставим курсор в их последнюю ячейку, открываем окно «Формула» («Работа с таблицами» — вкладка «Макет» — раздел «Данные» — кнопка «Формула»).

Как посчитать медиану?

Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.

Как вывести среднее значение?

Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.

Как найти среднее значение показателя?

В математике среднее арифметическое — это среднее число, которое получается, если сложить несколько чисел и разделить результат на количество этих чисел. Это не единственный способ вычисления среднего числа, но именно о нем большинство людей думает, когда речь идет о среднем.

Как найти среднее значение скорости?

Чтобы найти среднюю скорость, нужно разделить весь путь, пройденный объектом, на все время его движения.

Что такое среднее значение величины?

Среднее значение — Среднее значение числовая характеристика множества чисел или функций; некоторое число, заключённое между наименьшим и наибольшим из их значений.

Что такое среднее значение в математике пример?

Среднее арифметическое – это частное от деления суммы чисел на их количество. Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.

Что такое среднее арифметическое значение?

Средним арифметическим нескольких чисел называют сумму этих чисел, делённую на количество слагаемых. Среднее арифметическое = сумма всех чисел количество слагаемых .