Как найти среднее время в квадрате

Исследование переключения внимания в условиях активного выбора полезной информации (по таблице Шульте).

Исследовать скорость переключения внимания, работоспособность и упражняемость в условиях активного выбора полезной информации.

• Определить время (в с) выбора испытуемым по порядку цифр от 1 до 25 в 5 квадратах.
• Определить среднее время поиска цифр в квадрате.
• Начертить график, на котором по оси абсцисс отложить номера квадратов (1, 2, 3, 4, 5), а по оси ординат — время поиска всех цифр в соответствующем квадрате.

Ход работы. Испытуемому исследователь дает инструкцию — работать максимально быстро и внимательно. Затем исследователь замечает время по секундомеру, а испытуемый показывает числа от 1 до 25, называя их вслух. Исследователь определяет время, потраченное испытуемым для поиска 25 цифр по порядку сначала в первом, а затем во 2, 3, 4 и 5 квадратах. Исследователь отмечает в тетради время для каждого квадрата. Затем вычисляют среднее время для одного квадрата (поиска цифр в одном квадрате) и выражают графически. Делают вывод о переключаемости внимания, работоспособности и упражняемости.

СТИМУЛЬНЫЙ МАТЕРИАЛ (таблица Шульте)

Покажите по порядку числа от 1 до 25, называя их вслух (с максимальной скоростью)

21	12	7	1	20
6	15	17	3	18
19	4	8	25	13
24	2	22	10	5
9	14	11	23	16

14	18	7	24	21
22	1	10	9	6
16	5	8	20	11
23	2	25	3	15
19	13	17	12	4

22	25	7	21	11
6	2	10	3	23
17	12	16	5	18
1	15	20	9	24
19	13	4	14	8

9	9	11	23	20
14	25	17	1	6
3	21	7	19	13
18	12	24	16	4
8	15	2	10	22

5	14	12	23	2
18	25	7	24	13
11	3	20	4	18
8	10	19	22	1
21	15	9	17	6

Похожие материалы в разделе Психологический практикум:

• Деловая игра «Кадровый вопрос»
• Тест «Особенности творческого воображения»
• Скрининг-тест на злоупотребление наркотиками Dast (Drug abuse screening test)
• Методика измерения уровня тревожности Тейлора
  адаптация Т. А. Немчинова
• Беседа – интервью для изучения психологических особенностей личности «трудных» школьников
• Методика «Лесенка»
• Тест структуры интеллекта (TSI) Р. Амтхауэра (продолжение)
• Тест «Ваш стиль работы с документами»
• Нормы профессиональной этики для разработчиков и пользователей психодиагностических методик
• Изучение уровня притязаний детей в разных видах деятельности

Средняя квадратическая

Используется в тех случаях, когда при
замене индивидуальных значений признака
на среднюю величину необходимо сохранить
неизменной сумму квадратов исходных
величин.

Главная сфера её использования –
измерение степени колеблемости
индивидуальных значений признака
относительно средней арифметической
(среднее квадратическое отклонение).
Кроме этого, средняя квадратическая
применяется в тех случаях, когда
необходимо вычислить средний величину
признака, выраженного в квадратных или
кубических единицах измерения (при
вычислении средней величины квадратных
участков, средних диаметров труб, стволов
и т. д.).

Средняя квадратическая рассчитывается
в двух формах:

– как простая

(4.21)

как взвешенная

(4.22)

Все степенные средние различаются
между собой значениями показателя
степени.При этом, чем выше
показатель степени, тем большеколичественное значение среднего
показателя:

(4.23)

Это свойство степенных средних называется
свойством мажорантности средних.

Таким образом, выбор вида среднего
показателя оказывает существенное
влияние на его численную величину. Выбор
вида средней определяется в каждом
отдельном случае путем анализа исследуемой
совокупности, изучения содержания
явления. Степенная средняя выбрана
правильно, если на всех этапах
вычислений не меняется её логическая
формула, т.е. реально сохраняется
социально-экономическое содержание
усредняемого признака.

Особый вид средних показателей –
структурные средние. Они
используются при изучении внутреннего
строения рядов распределения значений
признака. К ним относятся мода и медиана.

Мода и медиана характеризуют значение
признака у статистической единицы,
занимающей определенное положение в
вариационном ряду.

Мода (Mo)
– наиболее часто встречаемое значение
признака в совокупности. Мода
широко используется в статистической
практике при изучении
покупательского спроса, регистрации
цен и др.

Медиана (Me)
– значение
признака у статистической единицы,
стоящей в середине ранжированного ряда
и делящей совокупность на две равные
по численности части.

Для дискретных вариационных
рядов Mo
и Me
выбираются в
соответствии с определениями: мода –
как значение признака с наибольшей
частотой
n_i
; положение медианы
при нечетном объеме совокупности
определяется ее номером
,
гдеN
– объем статистической совокупности.
При четном объеме ряда медиана равна
средней из двух вариантов, находящихся
в середине ряда.

Медиану используют как
наиболее надежный показатель типичного
значения неоднородной
совокупности, так как она нечувствительна
к крайним
значениям признака, которые могут
значительно отличаться от
основного массива
его значений. Кроме этого, медиана
находит практическое
применение вследствие особого
математического свойства:
.

Рассмотрим определение
моды и медианы на следующем примере:

Имеется ряд распределения
рабочих участка по уровню квалификации.
Данные приведены в таблице 4.4.

Таблица 4.4 – Распределения рабочих
участка по уровню квалификации

№ группы	Разряд рабочих	Число рабочих	Накопленная частота
1	1	3	3
2	2	5	8
3	3	9	17
4	4	14	31
5	5	10	41
6	6	9	50
Всего	–	50	–

Мода выбирается по
максимальному значению частоты: при
n_max
= 14,
Mo
= 4, т.е. чаще всего
встречается 4-ый разряд. Для нахождения
медианы Me
определяются
центральные единицы (N
+1)/2
. Это 25 и 26-ая единицы.
По накопленным частотам определяется
группа, в которую попадают эти единицы.
Это 4-ая группа, в которой значение
признака равно 4. Таким образом, Me
= 4, это означает,
что у половины рабочих разряд ниже 4-го,
а у другой – выше четвертого.

В интервальном ряду значения
Mo
и Me
вычисляются более
сложным путем.

Мода определяется следующим образом:

• По
максимальному значению частоты
определяется интервал, в котором
находится значение моды. Он называется
модальным.

• Внутри
модального интервала значение моды
вычисляется по формуле:

(4.24)

где
–
нижняя граница модального интервала;

a_Мо
– ширина модального
интервала;

n_Мо
,
n_Мо-1,

n_Мо+1
– соответственно
частоты модального, предмодального
(предшествующего модальному) и
постмодального (следующего за модальным)
интервалов.

Для расчета медианы в интервальных
рядах используется следующий подход:

• По
накопленным частотам находится медианный
интервал.

Медианным называется интервал, содержащий
центральную единицу.

• Внутри
медианного интервала значение Me
определяется по
формуле:

(4.25)

где
–
нижняя граница медианного интервала;

a_Ме
-ширина медианного
интервала;

N – объем статистической совокупности;

N
_Ме-1–
накопленная частота предмедианного
интервала;

n
_Ме
– частота медианного
интервала.

Расчет моды и медианы для
интервального ряда распределения
рассмотрим на примере ряда распределения
рабочих по стажу (табл. 4.5).

Таблица 4.5 – Распределение рабочих
участка по стажу

№ группы	Интервал	аi	ni	Ni
1	0	4	4	6	6
2	4	8	4	8	14
3	8	12	4	11	25
4	12	16	4	13	28
5	16	20	4	6	44
6	20	24	4	4	48
7	24	28	4	2	50
Всего	0	28	28	50	–

Расчет Mo:

• Максимальная частота
n_max
= 13, она
соответствует четвертой группе,
следовательно, модальным является
интервал с границами 12 – 16 лет.

• Моду рассчитаем по формуле:

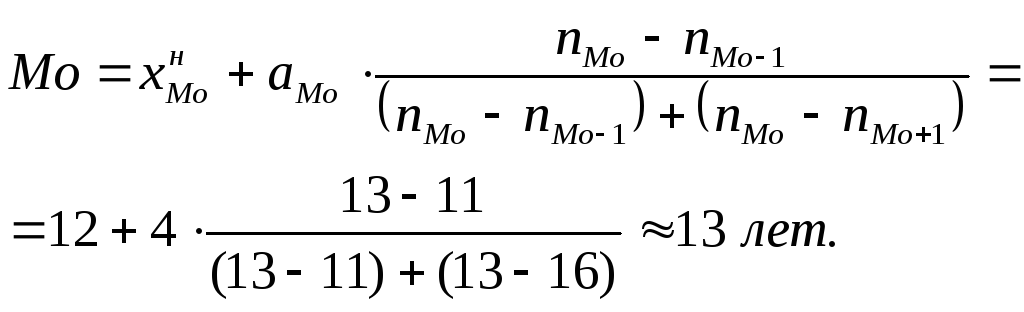
Чаще всего встречаются рабочие со стажем
работы около 13 лет.

Мода не находится в середине модального
интервала, она смещена к его нижней
границе, связано это со структурой
данного ряда распределения (частота
предмодального интервала значительно
больше частоты постмодального интервала).

Расчет медианы:

• По графе накопленных частот определяется
медианный интервал. Он содержит 25 и
26-ую статистические единицы, которые
находятся в разных группах – в 3-ей и
4-ой. Для нахождения Me
можно использовать любую из них.
Расчет проведем по 3-ей группе:

Такое же значение Me
можно получить при её расчете по
4-ой группе:

При сдвоенном центре Me
всегда находится на стыке
интервалов, содержащих центральные
единицы. Вычисленное значениеMe
показывает, что у первых 25 рабочих
стаж работы – менее 12 лет, а у оставшихся
25-ти, следовательно, – более 12 лет.

Моду можно определить графически по
полигону распределения в дискретных
рядах, по гистограмме распределения –
в интервальных, а медиану – по кумуляте.

Для нахождения моды в интервальном ряду
правую вершину модального прямоугольника
нужно соединить с правым верхним углом
предыдущего прямоугольника, а левую
вершину – с левым верхним углом
последующего прямоугольника. Абсцисса
точки пересечения этих прямых и будет
модой распределения.

Для определение медианы высоту наибольшей
ординаты кумуляты, соответствующей
общей численности совокупности, делят
пополам. Через полученную точку проводят
прямую, параллельную оси абсцисс, до
пересечения ее с кумулятой. Абсцисса
точки пересечения является медианой.

Кроме Mo иMe в вариантных
рядах могут быть определены и другие
структурные характеристики – квантили.
Квантили предназначены для более
глубокого изучения структуры ряда
распределения.Квантиль – это
значение признака, занимающее определенное
место в упорядоченной по данному признаку
совокупности. Различают следующие виды
квантилей:

– квартили – значения признака,
делящие упорядоченную совокупность на
4 равные части;

– децили – значения признака, делящие
совокупность на 10 равных частей;

– перцентели – значения признака,
делящие совокупность на 100 равных частей.

Таким образом, для характеристики
положения центра ряда распределения
можно использовать 3 показателя: среднее
значениепризнака,мода, медиана.

При выборе вида и формы конкретного
показателя центра распределения
необходимо исходить из следующих
рекомендаций:

– для устойчивых социально-экономических
процессов в качестве показателя центра
используют среднюю арифметическую.
Такие процессы характеризуются
симметричными распределениями, в которых

= Me
= Mo;

– для неустойчивых процессов положение
центра распределения характеризуется
с помощью Mo илиMe. Для
асимметричных процессов предпочтительной
характеристикой центра распределения
является медиана, поскольку она занимает
положение между средней арифметической
и модой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вычисление разницы во времени

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).

Предположим, вам нужно узнать, сколько времени требуется для сотрудника, чтобы завершить операцию сборки, или Быстрый заказ на питание, который будет обрабатываться в часы пик. Существует несколько способов расчета разницы между двумя значениями.

Представление результата в стандартном формате времени

Для представления результатов в стандартном формате времени (часы: минуты: секунды) можно использовать два подхода. Оператор вычитания (—) используется для определения разницы между временем, а затем выполните одно из указанных ниже действий.

Примените пользовательский код формата к ячейке, выполнив указанные ниже действия.

На вкладке Главная в группе число щелкните стрелку рядом с полем Общие и выберите пункт другие числовые форматы.

В диалоговом окне Формат ячеек в списке Категория выберите пункт другой , а затем в поле тип выберите настраиваемый формат.

Чтобы отформатировать значения параметров, используйте функцию текст .Если вы используете коды форматов времени, часы не всегда превышают 60, а секунды не предельной, а в секундах — 60.

Пример таблицы 1: результат представлен в стандартном формате времени

Скопируйте приведенную ниже таблицу на пустой лист, а затем при необходимости измените ее.

Как найти среднее арифметическое число в Excel

Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.

Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.

Как найти среднее арифметическое чисел?

Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.

Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:

1. Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:H1 и нажимаем ВВОД.
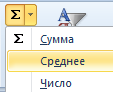
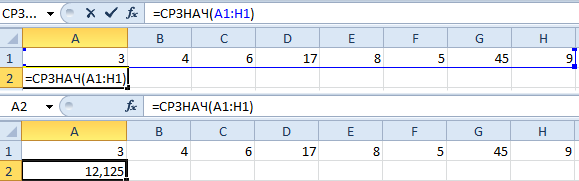
2. В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
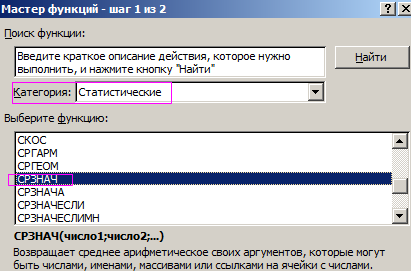
3. Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».

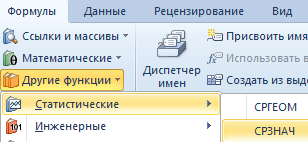
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).

Теперь посмотрим, что еще умеет функция СРЗНАЧ.

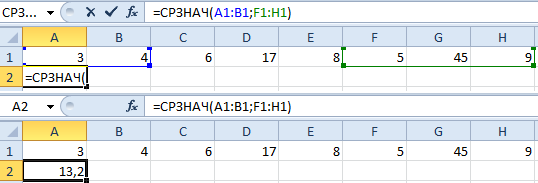
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:

Среднее значение по условию

Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().

Найти среднее арифметическое чисел, которые больше или равны 10.

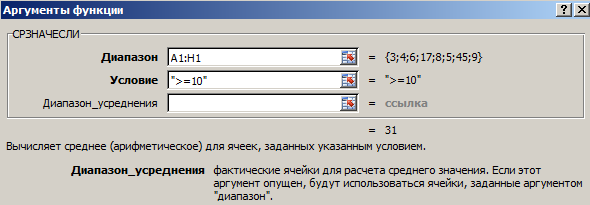Результат использования функции СРЗНАЧЕСЛИ по условию «>=10»:

Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.

Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.

Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».

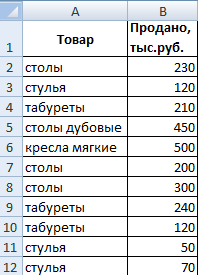
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.

В результате вычисления функции получаем следующее значение:

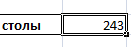
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.

Как посчитать средневзвешенную цену в Excel?

Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:

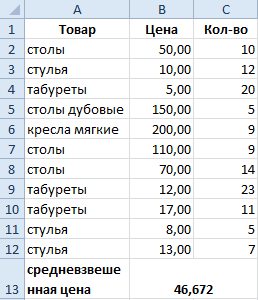
Как мы узнали средневзвешенную цену?

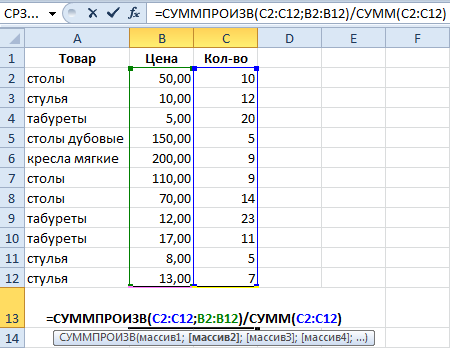
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.

Среднее квадратическое отклонение: формула в Excel

Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.

Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.

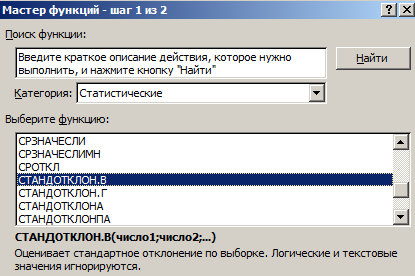
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:

среднеквадратическое отклонение / среднее арифметическое значение

Формула в Excel выглядит следующим образом:

СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).

Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.

Как в Excel посчитать время

Достаточно большой популярностью обладает табличный редактор Microsoft Office Excel. Это программа способна производить различные вычисления не только со стандартными числами. Она также способна работать с временными данными, такими как: часы, минуты и секунды. Для временных вычислений нужно использовать специальные формулы.

Инструкция

1. Если вам потребовалось вычислить определенный интервал времени в программе Excel, не спишите применять сложные математические формулы. Большинство подсчетов можно произвести при помощи простейших математических действий, таких как сложение и вычитание. Главное установить нужный формат ячеек.
2. Для начала вам нужно выделить группу ячеек, в которой будут расположены временные значения. Кликните по выделенной группе или одной ячейке правой клавишей мыши и в открывшемся меню нажмите на команду «Формат ячеек».
3. Будет запущенно новое диалоговое окно, в нем нужно перейти на вкладку «Число». В левой части этого окна укажите пункт «Время», в правой части окна появятся настройки данного формата. 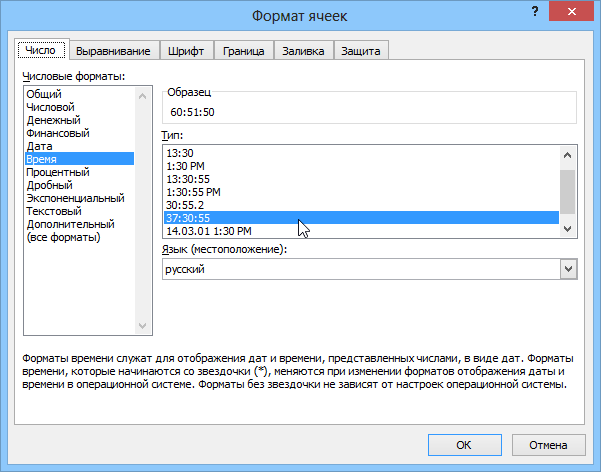Функция «Формат ячеек»

Выберите подходящий вид временного результата и нажмите кнопку ОК.

После присвоения ячейкам временного формата, введите в нужные ячейки значения время в формате XX:XX или XX:XX:XX. Теперь выберите ячейку для вывода результата, в поле для ввода формулы впишите знак «Равно» и кликните по ячейке с конечным значением. Теперь впишите знак «минус» и нажмите на ячейку с начальным значением. Нажмите ввод.

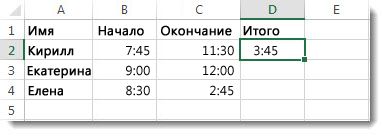Пример: если вам нужно вычислить интервал времени от 11:20:20 до 13:30:00, эти данные должны быть вписаны в ячейки А1 и В1 соответственно, а в ячейке с результатом (например, С1) должна быть формула: =В1-А1. Если формат ячеек указан верно, то должен быть выведен результат 2:9:40. Вычисление интервала времени

В том случае, если вам необходимо подсчитать несколько временных значений, то просто растяните маркер автоматического заполнения от ячейки С1 на нужную группу результатов.

Для того, чтобы вычислить сумму всех полученных результатов воспользуйтесь стандартной функцией сложения. Укажите ячейку, в которой должен быть выведен общий результат, и выберите команду Fx, в загрузившемся окне укажите опцию СУММ. Обозначьте все ячейки, результат из которых нужно подсчитать. Нажмите клавишу Enter, в ячейке с итоговым значением должна быть формула: =СУММ(С1:С5), если вы выбрали ячейки от С1 до С5. Обратите внимание, что всем этим ячейкам должен быть присвоен временной формат.

Советуем использовать в работе только лицензионную версию Microsoft Excel, которая входит в пакет программ Microsoft Office 2016. Купить данную программу вы можете у нас в нашем интернет-магазине.

Видео: Сложение значений времени в Excel

Как рассчитать среднее время в Excel (если сумма часов больше, чем 24)

У меня есть такие значения времени, как 10:00, 8:50, 9:45 и т.д. (Формат 24 часа). Я хочу знать, как я могу вычислить среднее значение этих 3 пунктов, если сумма часов больше 24 (если меньше, то нет проблем)?

Спасибо всем. Он работает, если просто введите значения в ячейках и попытайтесь найти среднее значение, но оно работает странно, если я использую время, которое уже является результатом моего расчета. Вот скриншот:

Как и любые другие числовые значения (например, с помощью функции AVERAGE()).

Используйте маску форматирования:

если вы хотите отобразить более 24 часов (например, для функции SUM()).

Вы пытались использовать функцию AVERAGE ?

Я тестировал его в соответствии с вашими значениями, и это дает мне правильное среднее время.

Вычисление среднего числа раз или списка направлений ветра можно было бы сравнить с вычислением среднего числа векторов (значений, содержащих как направление, так и величину). Поэтому необходимо приравнивать значения времени к их соответствующим положениям на единичном круге, выводить их значения перпендикулярных компонент и суммировать их так же, как в случае принятия «среднего» любой такой формы циклической группы.

Скажем, у вас есть два раза, 23:00 и 01:00, тогда обычный средний расчет (sumproduct/count) оставит вас с неправильным значением 12:00 [(23 + 1)/2] вместо правильного 24: 00/00:00. Если вы, однако, считаете 23:00 равным вектору 1 12 янв. ’15 в 7:00

Один из методов — преобразование каждого времени ячейки в секунды, затем среднее значение этих секунд и, наконец, преобразование в формат hh: mm: ss

Как в excel посчитать среднее время

Excel предсталяет собой табличный процессор. Его можно использовать для создания разнообразных отчетов. В данной программе очень удобно производить разные вычисления. Многие не используют и половину возможностей Excel.

Найти средние значение чисел может понадобиться в школе, а также во время работы. Классическим способ определения среднего арифметического без использования программ заключается в складывании всех чисел, а затем полученную сумму нужно разделить на количество слагаемых. Если числа достаточно крупные или для отчетности необходимо выполнить операцию много раз, вычисления могут занять много времени. Это нерациональная трата сил и времени, намного лучше воспользоваться возможностями Excel.

Поиск среднего арифметического

Многие данные уже изначально фиксируются в Excel, если же этого не происходит необходимо перенести данные в таблицу. Каждая цифра для расчета должна находится в отдельной ячейке.

Способ 1: Рассчитать среднее значение через «Мастер функций»

В этом способе необходимо прописать формулу для расчета среднего арифметического и применить ее для указанных ячеек.

Выделить любую ячейку в таблице нажать кнопку «Вставить функция».

В новом открывшемся окне необходимо найти поле «Категория», указать «Статические» с помощью которого задается конкретная функция для расчета.

В данной ситуации необходимо найти среднее арифметическое. Подходящей функцией будет «СРЗНАЧ», найти ее можно легко в середине списка, он располагается по алфавиту.

Перед применением функции открывается еще одно окно, в нем необходимо указать ячейки, в которых располагаются слагаемые для высчитывания результата.

Последним действием будет нажатие на кнопку «ОК», результат появляется в выбранной в первом шаге ячейке.

Основное неудобство этого способа в том, что приходится вручную вводить ячейки для каждого слагаемого. При наличии большого количества чисел это не слишком удобно.

Способ 2: Автоматический подсчет результата в выделенных ячейках

В этом способе расчет среднего арифметического осуществляется буквально за пару кликов мышью. Очень удобно для любого количества чисел.

Выделить ячейки, в которых имеются слагаемые будущей формулы. Лучше оставить одну клетку внизу пустой, в ней будет высвечиваться результат.

Перейти в меню во вкладку «Формулы», там выбрать в левом верхнем углу «Автосумма». При нажатии на стрелку, чтобы раскрыть все функции рядом с этой кнопкой, открываются несколько функций быстрого набора. Там следует выбрать «Среднее».

Недостатком этого способа является расчет среднего значения только лишь для чисел, расположенных рядом. Если необходимые слагаемые разрознены, то их не получится выделить для расчета. Невозможно даже выделить два столбца, в таком случае результаты будут представлены отдельно для каждого из них.

Способ 3: Использование панели формул

Еще один способ перейти в окно функции:

Выбрать вкладку «Формулы», навести курсор мыши на «Другие функции», выбрать «Статические» и «СРЗНАЧ».

Открывается окно функции, в которой можно указать ячейки просто выделив их в таблице или же вписав каждую отдельно.

Нажать «ОК» и увидеть результат в свободной ячейке.

Самый быстрый способ, при котором не нужно долго искать в меню необходимы пункты.

Способ 4: Ручной ввод

Не обязательно для высчитывания среднего значения использовать инструменты в меню Excel, можно вручную прописать необходимую функцию.

Найти строку для ввода разнообразных формул.

Ввести необходимые числа согласно шаблону:
=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число))

Быстрый и удобный способ для тех, кто предпочитает создавать формулы своими руками, а не искать готовые в меню программы.

Благодаря этим возможностям очень легко рассчитать среднее значение любых чисел, вне зависимости от их количества, можно также составлять статистические данные без подсчетов вручную. С помощью инструментов программы Excel любые расчеты сделать намного легче, чем в уме или же с помощью калькулятора.