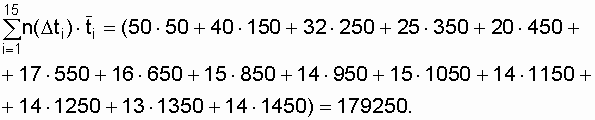Среднее
время восстановления – это математическое
ожидание времени восстановления
работоспособного состояния объекта
после отказа . Из определения следует,
что
,
(2.17)
где
n
–
число восстановлений, равное числу
отказов;
– время, затраченное на восстановление
(обнаружение, поиск причины и устранение
отказа), в часах.
Показатель
можно определить и на основании
статистических данных, полученных для
М
однотипных
восстанавливаемых объектов. Структура
расчетной формулы остается той же:
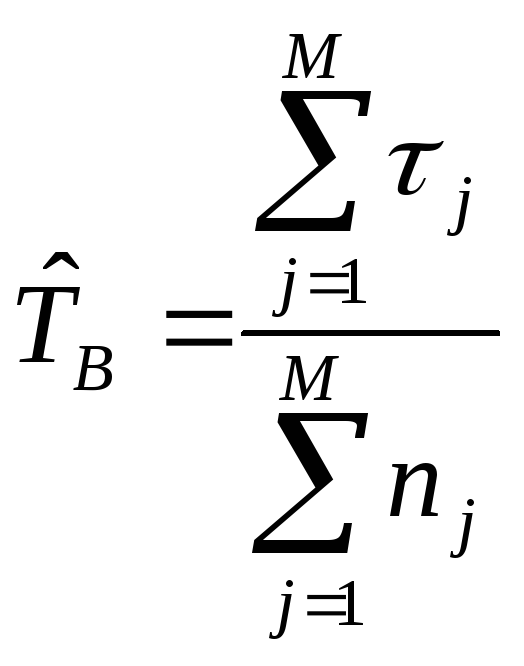
где
М
– количество однотипных объектов, для
каждого из которых определено общее
время
восстановления
за заданное время наблюдений;
,
где
– время восстановления j-го
объекта после i-го
отказа; nj
–
количество восстановлений j-го
объекта за время наблюдений, причем
1≤j≤M.
-
2.3.2. Интенсивность восстановления
Интенсивность
восстановления – это отношение условной
плотности вероятности восстановления
работоспособного состояния объекта,
определенной для рассматриваемого
момента времени при условии, что до
этого момента восстановление не было
завершено, к продолжительности этого
интервала.
Статистическая
оценка этого показателя находится как
,
(2.19)
где
nв(t)
– количество восстановлений однотипных
объектов за интервал t;
– среднее количество объектов, находящихся
в не восстановленном состоянии на
интервале t.
В
частном случае, когда интенсивность
восстановления постоянна, то есть (t)
==
const,
вероятность восстановления за заданное
время t
подчиняется экспоненциальному закону
[3, 13, 21] и определяется по выражению
.
(2.20)
Этот
частный случай имеет наибольшее
практическое значение, поскольку
реальный закон распределения времени
восстановления большинства
электроэнергетических объектов (поток
восстановлений) близок к экспоненциальному
[10, 14]. Используя свойства этого
распределения, запишем очень важную
зависимость:
,
а также
. (2.21)
В
дальнейшем эта взаимосвязь между Тв
и
будет часто использоваться при анализе
восстанавливаемых систем.
При
более детальных расчетах показателей
надежности ремонтируемых (восстанавливаемых)
объектов определяется такой показатель
ремонтопригодности, как процентное
время восстановления .
Это время в течение которого восстановление
работоспособности объекта будет
осуществлено с вероятностью
, выраженной в процентах [7].
-
2.4. Комплексные показатели надежности
-
2.4.1. Коэффициент готовности
-
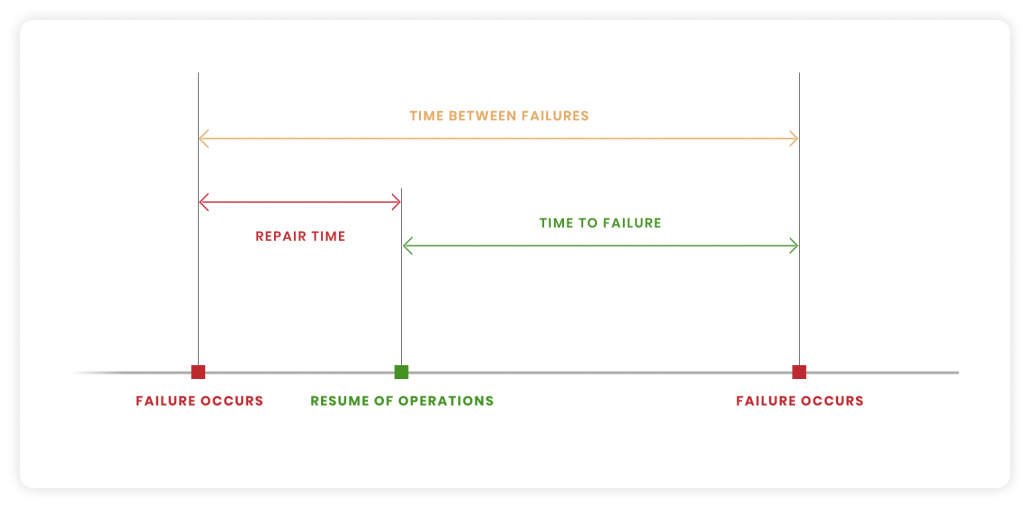
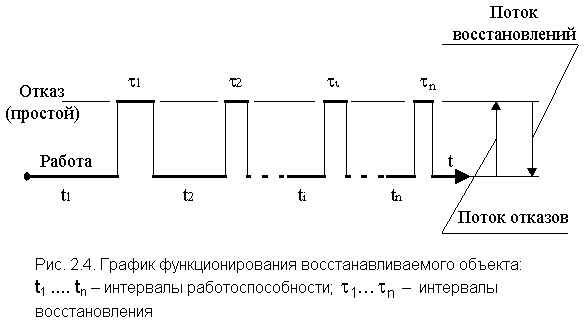
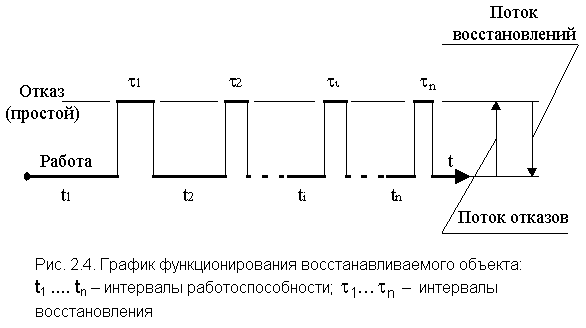
Процесс
функционирования восстанавливаемого
объекта можно представить как
последовательность чередующихся
интервалов работоспособности и
восстановления (простоя).
Коэффициент
готовности – это вероятность того, что
объект окажется в работоспособном
состоянии в произвольный момент времени,
кроме планируемых периодов, в течение
которых применение объекта по назначению
не предусматривается [7]. Математическое
определение этого показателя дано ниже
(разд. 7) при анализе надежности
восстанавливаемых систем.
Этот
показатель одновременно оценивает
свойства работоспособности и
ремонтопригодности объекта.
Для
одного ремонтируемого объекта коэффициент
готовности
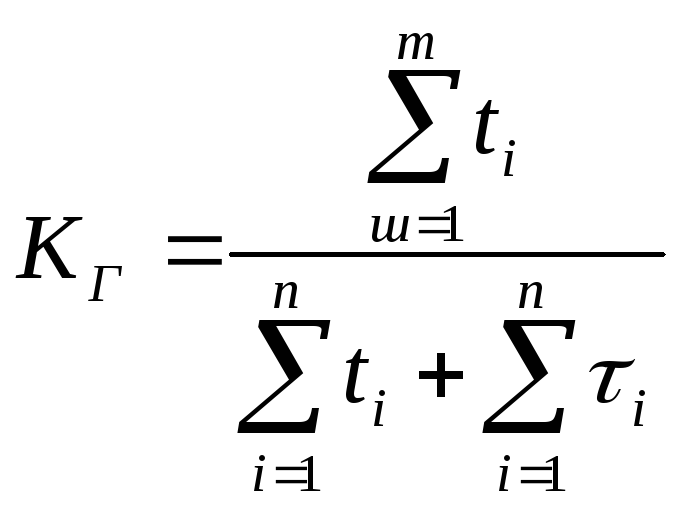
,
.
(2.23)
Из
выражения 2.23 видно, что коэффициент
готовности объекта может быть повышен
за счет увеличения наработки на отказ
и уменьшения среднего времени
восстановления. Для определения
коэффициента готовности необходим
достаточно длительный календарный
срок функционирования объекта.
Зависимость
коэффициента готовности от времени
восстановления затрудняет оценку
надежности объекта, так как по КГ
нельзя судить о времени непрерывной
работы до отказа. К примеру, для одного
и того же численного значения КГ
можно иметь малые интервалы
и ti
(см. рис. 2.4) и значительно большие. Таким
образом можно доказать, что на конкретном
интервале работоспособности вероятность
безотказной работы будет больше там,
где больше ti,
хотя за этим интервалом может последовать
длительный интервал простоя .
Коэффициент готовности является удобной
характеристикой для объектов, которые
предназначены для длительного
функционирования, а решают поставленную
задачу в течение короткого промежутка
времени (находятся в ждущем режиме),
например, релейная защита, контактная
сеть (особенно при относительно малых
размерах движения), сложная контрольная
аппаратура и т.д.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1.3.2. Показатели ремонтопригодности.
Свойство ремонтопригодности выше
определено как свойство объекта, характеризующее его приспособленность к
поддержанию и восстановлению работоспособного состояния путем технического
обслуживания и ремонта и реализуется в течение некоторого времени, которое
называется временем восстановления.
Время становления – |
продолжительность восстановления работоспособного состояния |
Время становления
складывается из времен, затрачиваемых на отыскание и устранение отказа,
проведение необходимых отладок и проверок, что бы убедиться в восстановлении
работоспособности объекта. Время восстановления отсчитывается от момента начала
проявления отказа (при условии, что в этот момент начинается устранение отказа)
до момента восстановления работоспособности объекта.
Время восстановления является
случайной величиной и обозначается h
.
Основными показателями
ремонтопригодности являются вероятность восстановления (), среднее время восстановления (
) и интенсивность восстановления (
).
Вероятность восстановления – |
вероятность того, что время восстановления работоспособного |
|
|
(1.2.17) |
Вероятность восстановления является
функцией распределения случайной величины времени восстановления.
Среднее время восстановления – |
математическое ожидание времени восстановления работоспособного |
|
|
(1.2.18) |
где –
плотность распределения времени восстановления.
Интенсивность восстановления – |
плотность условной вероятности восстановления работоспособного |
|
|
(1.2.19) |
Следует отметить, что интенсивность восстановления в
определенном смысле аналогична интенсивности отказов (слово «отказ» заменяется
словом «восстановление».
1.2.3. Комплексные показатели надежности, характеризующие одновременно безотказность
и ремонтопригодность.
Комплексный показатель надежности – |
показатель, характеризующий несколько свойств, составляющих |
Основными комплексными
показателями данной группы являются следующие.
|
Коэффициент готовности – |
вероятность того, что объект окажется в работоспособном |
Существует нестационарный
коэффициент готовности, который зависит от произвольного, но фиксированного
момента времени t (. Есть и стационарный коэффициент
готовности, который равен
|
|
(1.2.20) |
Физический смысл коэффициента готовности – это доля
времени на достаточно большом интервале времени, когда объект был
работоспособен. Далее будет показано, что коэффициент готовности равен
|
|
(1.2.21) |
где – средняя наработка до
отказа, а – среднее время восстановления.
Коэффициент оперативной готовности – |
вероятность того, что объект окажется в работоспособном |
Существуют стационарный и
нестационарный коэффициенты оперативной готовности.
Первый зависит от произвольного но фиксированного момента времени t, и от заданного интервала времени t, в течение которого объект должен работать (). Стационарный коэффициент
готовности равен
|
|
При некоторых определенных условиях и когда момент, от
которого откладывается интересующий нас интервал времени t,
достаточно удален от 0, будет справедливо
|
|
где – стационарный коэффициент
готовности, а – вероятность безотказной
работы объекта в течение времени t, отложенного
от некоторого, достаточно удаленного от 0, момента.
Коэффициент технического использования – |
это отношение математического ожидания суммарного времени |
Коэффициент готовности и
коэффициент оперативной готовности в [18] определены только для того случая,
когда объект в любой момент времени может находиться в одном из двух состояний:
либо работоспособен, либо неработоспособен (находится на восстановлении).
Коэффициент технического использования следует рассматривать в предположении,
что объект может быть в любой момент в одном из трех состояний: либо работоспособен,
либо неработоспособен (восстанавливается), либо находится на техническом
обслуживании.
1.2.4. Показатели долговечности.
Свойство долговечности и
связанное с ним понятие предельного состояния определены в главе 1. Это
свойство может быть реализовываться как в течение некоторой наработки (тогда
говорят о ресурсе), так ив течение календарного времени (тогда говорят о сроке
службы). В любом случае время (наработка или календарное время) от начала работы
объекта до его попадания в предельное состояние является непрерывной случайной
величиной.
Основными показателями ресурса и срока
службы являются.
|
Средний ресурс – |
математическое ожидание ресурса. |
|
Гамма-процентный ресурс – |
календарная продолжительность эксплуатации, в течение |
|
Назначенный ресурс – |
суммарная наработка, при достижении которой эксплуатация |
|
Средний срок службы – |
математическое ожидание срока службы. |
|
Гамма-процентный срок службы – |
календарная продолжительность эксплуатации, в течение |
|
Назначенный срок службы – |
календарная продолжительность эксплуатации, при достижении |
Можно рассматривать назначенный ресурс (срок службы)
до первого капитального ремонта, между капитальными ремонтами, до списания и
т.п.
1.2.5. Показатели сохраняемости.
Определение свойства
сохраняемости приведено в главе 1. С позиции надежности предполагается,
что объект становится на хранение или начинает транспортироваться в исправном
состоянии. Свойства сохраняемости также реализуется в течение некоторого
времени, которое называется сроком сохраняемости. (электроэнергия)
|
Срок сохраняемости – |
календарная продолжительность хранения и (или) транспортирования |
Срок сохраняемости в теории надежности
рассматривается как случайная величина.
Сохраняемость характеризуется следующими основными
показателями.
|
Средний срок сохраняемости – |
математическое ожидание срока сохраняемости. |
|
Гамма-процентный срок сохраняемости – |
срок сохраняемости, достигаемый объектом с заданной вероятностью |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
А сколько проработает ваша система? Это можно посчитать!
Уважаемые читатели Low-voltage Blog! В первой статье о создании систем видеонаблюдения я утверждал, что у проектировщика есть возможность посчитать вероятность работы системы за заданный промежуток времени. Сегодня мы обсудим этот вопрос подробней: с объяснениями «на пальцах» и страшными формулами 🙂 .
Содержание:
1. Термины
1.1 Коэффициент готовности
1.2 Средняя наработка на отказ
1.3 Среднее время восстановления
2 Метод расчёта коэффициента готовности
2.1 Система без резервирования элементов
2.2 Система со 100% резервированием элементов
2.3 Система с частичным резервированием
3 Рекомендации по выбору оборудования и общие выводы
3.1 Рекомендации при проектировании
3.2 Выводы для заказчиков и подрядчиков
Кому адресован этот блог и почему моему мнению можно доверять.
Мои контакты — пишите по любым интересующим вопросам, в том числе предложения о сотрудничестве.
Почему важно понимать вероятность работоспособности системы безопасности и других слаботочных систем в заданный промежуток времени? Очень просто — системы созданы, чтобы решить совершенно конкретную задачу заказчика (это в идеале 🙂 ). Если система не работает — она не решает эту задачу, проблему и т.п. Заказчик терпит убытки, вынужден принимать дополнительные меры безопасности и т.п. При заказе систем часто возникает вопрос — какого класса оборудование нужно взять? Нужно ли резервировать оборудование, и если нужно — то какое именно? Как обосновать перед заказчиком выбор оборудования и степень резервирования?
Ответом на все эти вопросы мы сегодня и займемся.
Статья основана на моей ранее изданной публикации на портале sec.ru. По уже озвучиваемым причинам сейчас она не доступна, как и весь портал. Поэтому публикую её в чуть измененном виде в Low-voltage Blog.
Существует класс заказчиков, для которых цена не является основополагающим фактором при согласовании технических решений. Как правило речь в таких случаях идет о крупных системах. Заказчик может руководствоваться различными соображениями. Чаще всего — стоимостью владения системой и рисками / убытками от неработоспособности системы. В таком случае в ТЗ прописывается желаемый коэффициент готовности системы (Instantaneous availability function) по ГОСТ 27.002-2015 Надежность в технике (ССНТ). Термины и определения.
Данная статья — попытка кратко описать методику обоснования выбора технических решений, особенности проектирования систем с учетом заданного коэффициент готовности, а так же преимущества данного подхода для заказчика перед стандартными подходами (использовать проверенное оборудование; оборудование, на которое есть максимальная скидка; самое дешёвое и т.п.).
1. Термины
Для начала необходимо определиться с терминами.
1.1 Коэффициент готовности
Коэффициент готовности (Instantaneous availability function) — вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени. Кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Практически коэффициент готовности определяется через среднее суммарное время простоя за заданный интервал времени. Коэффициент готовности Kг =(T – tпΣ) /T, где tпΣ — суммарное время простоя, а T — заданный интервал времени.
К примеру, если заказчик хочет получить систему, суммарное время простоя (неработоспособности) которой в год не должно превышать 1 день, то в задании на проектирование указывается Kг=(365-1)/365 = 0,9973. Можно убедится, что для заказчика в использовании коэффициента готовности нет особой сложности. Он интуитивно понятен, и при этом является комплексным показателем надежности системы. И пожалуй самое важное для заказчика — заявленные данные подрядчика легко проверяются на практике. Для этого достаточно скрупулезно записывать время простоя при эксплуатации, за исключением времени технического обслуживания и т.п., как видно из определения. Проверяемость данных — хорошая гарантия для заказчика, что подрядчик будет максимально тщательно относится ко всем заявляемым характеристикам оборудования.
1.2 Средняя наработка на отказ
Средняя наработка на отказ Mean operating time between failures (MTBF) — отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Фактически речь идет среднем времени нормального функционирования изделия. Оно вычисляется как отношение общего времени, в течение которого изделие находилось в эксплуатации (t), к общему количеству учитываемых отказов, F, которые возникли в течение времени t. MTBF= t / F(t) = 1 / λ, где λ — интенсивность отказов. Есть правда нюанс — отказ отказу рознь, надо различать учитываемые и не учитываемые отказы. Учитываемый отказ изделия является отдельным отказом, который влечёт потерю способности изделия выполнять требуемую функцию в связи с одним из нижеследующих событий:
- ошибка или поломка изделия, когда оно эксплуатируется в пределах установленных проектом предельных рабочих характеристик и условий окружающей среды;
- неправильная эксплуатация, обслуживание или испытание изделия, по причине предоставленной Подрядчиком документации.
Не учитываемый отказ изделия — любая ситуация отказа изделия, которая не входит в определение «учитываемого отказа», представленного выше, например:
- отказ, вызванный неправильным функционированием другого оборудования;
- отказ, вызванный человеческой ошибкой, за исключением случаев, когда он подпадает под определение «учитываемый отказ»;
- отказ, вызванный функционированием изделия за пределами своих проектных рабочих характеристик или условий окружающей среды.
На сегодняшний день данные по MTBF оборудования предоставляются большинством зарубежных и многими отечественными производителями. Так что особо останавливаться на данном параметре не будем. Отмечу только, что для центрального и периферийного оборудования величина MTBF может существенно отличаться, и это нормально. Безотказность работы центрального оборудования важнее для работоспособности системы в целом, нежели периферийного. Естественно, данные рассуждения перестают работать, если подрядчик начинает “кроить” систему. Экономить на компонентах (например вместо стоечных серверов использует обычные ПК).
Так же отмечу, что есть прямая связь между классом оборудования и величиной MTBF (естественно, чем выше класс — тем больше MTBF). Нередко заказчик помимо требования о значении коэффициента готовности указывает в задании на проектирование минимальные требования на MTBF оборудования, используемого в проекте. На мой взгляд это гораздо лучше и профессиональней, чем требование о использовании конкретного бренда и тем более конкретной марки оборудования. С одной стороны это ограничивает возможности участников тендера заниматься демпингом, используя некачественное дешевое оборудование. С другой стороны оставляет профессионалам возможность заниматься собственно проектной работой — подбирать оборудование в соответствии с задачей и техническим заданием).
1.3 Среднее время восстановления
Среднее время восстановления Mean time to repair (MTTR) — математическое ожидание времени восстановления работоспособного состояния объекта после отказа. Фактически речь идет о продолжительности корректирующего технического обслуживания – сумме периодов времени, которые были затрачены на обнаружение и локализацию отказа, демонтаж или ремонт дефектов оборудования, и выполнение необходимых проверок для восстановления нормальной работы оборудования. На мой взгляд сюда же нужно включать время заказа и доставки отказавшего оборудования (при отсутствии его в ЗИПе), если ремонт не возможен. На практике MTTR вычисляют как отношение общего времени, затраченного на оперативное корректирующее техническое обслуживание Tmc, которое было потрачено в течение заданного периода времени (t) для множества идентичных элементов, к общему числу учитываемых отказов F, которые потребовали корректирующего техобслуживания для этого множества элементов в рассматриваемом интервале времени.
MTTR= Tmc(t) / F(t) = 1 / µ, где µ: интенсивность восстановления.
К сожалению, с MTTR ситуация значительно хуже, чем с MTBF. Мне данные по MTTR оборудования попадались крайне редко. Поэтому зачастую данный параметр приходится прикидывать самостоятельно. Для этого общее время MTTR разбивается на следующий составляющие:
- обнаружение
- локализация
- демонтаж неисправного оборудования
- монтаж аналогичного из ЗИПа
- регулировка / настройка.
При отсутствии для данного типа оборудования ЗИПа, на мой взгляд, к предыдущим составляющим MTTR необходимо добавлять время заказа и поставки оборудования. Только так мы получим объективный коэффициент готовности системы (и соответственно правильное понимание надежности системы).
Как и в случае с MTBF, MTTR коррелирует с классом оборудования, хотя уже и в меньшей степени. Только зависимость для MTTR обратная — чем выше класс оборудования, тем MTTR меньше. За счёт чего это достигается? Есть разные факторы: системы высокого класса обычно имеют функции:
- диспетчеризации (что положительно сказывается на времени обнаружения)
- само-диагностики (уменьшает время локализации неисправности)
- центрального управления (что зачастую позволяет просто загружать все настройки вышедшего из строя оборудования без необходимости производить пусконаладочные работы)
- оборудование — свойствами модульности (например, возможность легкой замены блоков питания стоечного сервера — что ускоряет демонтаж неисправного модуля и монтаж запасного).
Но, как я уже неоднократно отмечал, на MTTR сильно влияют и чисто организационные моменты:
- наличие квалифицированного и обученного персонала у заказчика (или привлечение аутсорсинга подрядчика), желательно периодически тренируемого на действия при тех или иных нештатных ситуациях в системе
- наличие правильно сформированного ЗИПа
- и др.
Поэтому при написании задания на проектирование важно учитывать не только как систему реализовать, но и как её в дальнейшем успешно эксплуатировать.
2 Метод расчёта коэффициента готовности
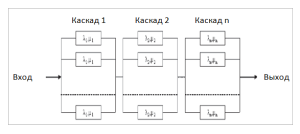
Любые системы можно условно разделить на последовательные, параллельные и последовательно-параллельные.
2.1 Система без резервирования элементов
Если отказ одного элемента оборудования приводит к отказу всей системы, и, если отказы не зависят друг от друга, то вся система называется последовательной. Фактически, речь идет о системе, в которой полностью отсутствует резервирование элементов.
Для наглядности представим центральную часть системы видеонаблюдения, состоящую из:
- энкодеров, осуществляющих запись с видеокамер
- декодеров, выводящих нужные видеопотоки на видеостену
- сетевого менеджера, управляющего всем этим оборудованием.
Для такой системы коэффициент готовности будет вычисляться следующим образом:
Коэффициент готовности для последовательных систем (без резервирования)
Т.е., к примеру, если система состоит из 1-го сетевого менеджера, 10 энкодеров и 10 декодеров, то Kг сист.= Kг сет.мен.* Kг энк.10 * Kг дек.10. Из приведенной формулы можно уже сделать первые очевидные выводы: надежность тем выше, чем больше MTBF и меньше MTTR, и тем меньше, чем больше элементов в последовательной системе, поскольку Kг всегда меньше 1. Соответственно чем система сложнее (больше элементов), тем труднее добиться высокой надежности.
2.2 Система со 100% резервированием элементов
Если функционирование 1-го из n элементов системы достаточно для функционирования всей системы, то вся система называется параллельной. Фактически, речь идет о системе со 100% резервированием. Для такой системы коэффициент готовности будет вычисляться следующим образом:
Коэффициент готовности для параллельной системы (полное резервирование элементов)
Останавливаться на параллельной системе долго не будем, потому как чисто параллельные системы встречаются не часто. Пример — система передачи извещений на пульт центральной охраны по нескольким независимым каналам связи отдельными устройствами.
2.3 Система с частичным резервированием
Для системы с резервированием элементов, которая представлена последовательно-параллельной системой, средний коэффициент готовности будет равен:
Коэффициент готовности для последовательно-параллельной системы (частичное резервирование)
где: Ki — количество компонентов с резервированием в подсистеме i, S — количество подсистем в полной системе.
Блок схема надёжности последовательно-параллельной системы (MTBF — µ, MTTR — λ).
Блок-схема последовательно-параллельной системы
Для нашего примера с системой видеонаблюдения, мы должны будем резервировать элементы общей системы. Например, сетевой менеджер, энкодеры, декодеры. Допустим, мы остановились на системе с кратностью резервирования n+1, в таком случае коэффициент готовности будет равен:
Kг сист. = (1-(1-Kг сет.мен.)2) * (1-(1-Kг энк.)2) * Kг энк.9 * (1-(1-Kг дек.)2 * Kг дек.9.
Но тут нужно учесть один момент: данная формула применима, если для заказчика важна надежность как функции записи видеопотоков, так и функция отображения их на видеостене. Если, к примеру, отображение видео на видеостене — функция второстепенная, то для расчета коэффициента готовности декодеры вполне можно не учитывать, величина коэффициента готовности при этом возрастёт:
Kг сист. = (1-(1-Kг сет.мен.)2) * (1-(1-Kг энк.)2) * Kг энк..
Данный факт ещё раз подчёркивает, что только заказчик может правильно расставить приоритеты по надёжности для своей системы. Задача подрядчика учесть пожелания заказчика и грамотно рассчитать коэффициент готовности и подобрать оборудование с учётом этого.
3 Рекомендации по выбору оборудования и общие выводы
3.1 Рекомендации при проектировании
Алгоритм проектирования для достижения заданного коэффициента готовности может быть, например, такой.
- Если система достаточно крупная (сотни элементов), то имеет смысл отдельно рассчитывать коэффициент готовности для центральной части системы и периферии. Иначе влияние ваших технических решений на общую надежность системы будет не заметно на фоне большого количества не резервируемых элементов периферии. К тому же, как я уже отмечал выше, для большой части заказчиков надежность работы центральной части системы приоритетней, нежели периферии. Для примера с видео наблюдением работа энкодера и сетевого менеджера значительно важнее и приоритетней, чем одной случайно взятой видеокамеры, когда счет идет на сотни видеокамер и десятки энкодеров. Самой критичной частью системы этом случае будет сетевой менеджер. Именно его функции важно резервировать.
- После того, как принято решение рассчитывать ли отдельно коэффициент готовности для центральной и периферийной части системы, необходимо для каждого типа оборудования (для видео наблюдения это энкодеры, декодеры, сетевые менеджеры, и т.д.) найти сведения о MTBF и MTTR данного типа оборудования. Подсчитать его общее количество. Вычислить коэффициент готовности единичного оборудования каждого типа и для каждого типа оборудования — общий коэффициент готовности с учетом наличия или отсутствия резервирования по перечисленным выше формулам для последовательной (если нет резервирования), параллельной (если 100% резервирование) или последовательно-параллельной (для частичного уровня резервирования) системы.
- Коэффициент готовности всей системы в целом будет равен произведению общих коэффициентов готовности всех типов оборудования.
- Далее начинается процесс оптимизации технических решений для получения нужного коэффициента готовности системы.
Важно отметить, что сделав небольшую и не сложную таблицу в офисной программе мы получаем возможность практически мгновенно вычислять влияние принимаемых проектировщиком подрядчика решений на надежность системы в целом, приходя к нужной конкретному заказчику заданной надежности быстро и эффективно.
3.2 Выводы для заказчиков и подрядчиков
Итак, подведем итоги.
Коэффициент готовности является комплексных показателем надежности системы. Его можно вычислить двумя способами: теоретически через MTBF и MTTR оборудования системы при проектировании (вычисляется подрядчиком) и при эксплуатации системы практически через среднее суммарное время простоя (вычисляется заказчиком). Таким образом, коэффициент готовности обладает свойством проверяемости. Данный коэффициент позволяет подрядчику обосновывать принимаемые технические решения исходя из требуемой заказчиком надежности, а заказчику эффективно инвестировать собственные средства учитывая риски неработоспособности системы в течении n-го времени.
Для того, чтобы подрядчик смог грамотно рассчитать коэффициент готовности, заказчику необходимо оценить какое максимальное время простоя допустимо для той или иной функции системы на достаточно большом промежутке времени (обычно в течении года, но не обязательно, можно и любой другой период). К примеру заказчик владеет торгово-развлекательным центром (ТРЦ) и сдает имеющиеся помещения арендаторам. Чтобы грамотно составить задание на проектирование на систему автоматики жизнеобеспечения здания (ИТП, холодоснабжение, энергоснабжение и т.п.), нужно рассчитать допустимые убытки от неработоспособности или не полной работоспособности данных систем из-за недоступности соответствующих функций системы автоматики. Например, холодоснабжение актуально летом. Заказчик может прописать в задании на проектирование, что система автоматики для данной функции не должна находиться в отключенном состоянии дольше 1 дня в течении 3-х месяцев. А отсутствие автоматического управления отоплением заказчик готов терпеть не больше 3-х дней в течении 8-ми месяцев отопительного сезона. Отсутствие же управления и диспетчеризации системы электроснабжения допустимо не более 5-ти дней в течении года. Такие формулировки вполне достаточны для расчета надежности системы автоматики для ТРЦ. Думаю очевидно, что подобные рассуждения не сложно привести любому собственнику, заказчику систем у подрядчика.
Проектировщику подрядчика необходимо иметь в виду следующие соображения. Чем крупнее система, тем сложнее добиться надежности ее работы и, соответственно, высокого коэффициента готовности. Поэтому для крупных систем необходимо выбирать оборудование с высоким MTBF и низким MTTR. Находить в системе «узкие» места и резервировать оборудование. Рассчитать и включить в смету необходимый для надежной работы системы ЗИП, дать рекомендации к численности и квалификации обслуживающего персонала, периодичности технического обслуживания. Если система очень крупная (сотни единиц оборудования), то оправдано раздельное вычисление коэффициента готовности для центральной части системы и для периферии.
На сегодня эта вся информация, которой я хотел с вами поделиться, спасибо за уделенное время!
Уважаемые читатели блога, если Вы заметили в статье неточность, сложность в изложении материала либо некорректность используемых терминов — прошу написать в комментариях либо в личном сообщении, все замечания будут обязательно учтены и по-возможности исправлены все недочёты.
Жду ваших вопросов, комментариев и предложений.
Жмите кнопки социальных сетей, подписывайтесь на email рассылку, добавляйте блог в свою RSS-ленту, вступайте в группы блога в социальных сетях!
Все материалы данного блога принадлежат его автору. Использование без ссылки на данный блог с указанием авторства не допускается!
ЛЕКЦИЯ
2.
Основные показатели ремонтопригодности
Среднее время восстановления
Интенсивность восстановления
Комплексные показатели надежности
Коэффициент готовности
Коэффициент оперативной готовности
Коэффициент технического использования
Основные математические модели, наиболее часто используемые в расчетах
надежности
Распределение Вейбулла
Экспоненциальное распределение
Распределение Рэлея
Нормальное распределение (распределение Гаусса)
Примеры использования законов распределения в расчетах надежности
Определение показателей надежности при экспоненциальном законе распределения
Определение показателей надежности при распределении Рэлея
Определение показателей схемы при распределении Гаусса
3.5.4.
Пример определения показателей надежности неремонтируемого объекта по опытным
данным
2.3.
Основные показатели ремонтопригодности
При количественном описании этого свойства,
которое присуще только восстанавливаемому объекту, время восстановления
является случайной величиной, зависящей от целого ряда факторов: характера
возникшего отказа; приспособленности объекта (устройства, установки и др.)
к быстрому обнаружению отказа; квалификации обслуживающего персонала; наличия
технических средств; быстроты замены отказавшего элемента в объекте и др.
Время восстановления – это время, затраченное на обнаружение, поиск причины
отказа и устранения последствий отказа. Опыт показывает, что в сложных
электроустановках (системах) 70-90% времени восстановления приходится на
поиск отказавшего элемента [2, 15, 16, 17].
2.3.1.
Среднее время восстановления
Среднее время восстановления – это
математическое ожидание времени восстановления работоспособного состояния
объекта после отказа . Из определения следует, что
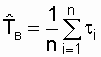
(2.17)
где n – число восстановлений, равное
числу отказов; – время,
затраченное на восстановление (обнаружение, поиск причины и устранение
отказа), в часах.
Показатель можно
определить и на основании статистических данных, полученных для М однотипных
восстанавливаемых объектов. Структура расчетной формулы остается той же:
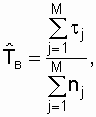
где М – количество однотипных объектов,
для каждого из которых определено общее время восстановления за
заданное время наблюдений;
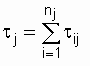
где – время восстановления
j-го объекта после i-го отказа; nj – количество восстановлений
j-го объекта за время наблюдений, причем .
2.3.2.
Интенсивность восстановления
Интенсивность восстановления – это
отношение условной плотности вероятности восстановления работоспособного
состояния объекта, определенной для рассматриваемого момента времени при
условии, что до этого момента восстановление не было завершено, к продолжительности
этого интервала.
Статистическая оценка этого показателя
находится как
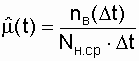
(2.19)
где nв(Dt)
– количество восстановлений однотипных объектов за интервал Dt; –
среднее количество объектов, находящихся в невосстановленном состоянии
на интервале Dt.
В частном случае, когда интенсивность
восстановления постоянна, то есть m(t)
=m= const, вероятность
восстановления за заданное время t подчиняется экспоненциальному закону
[3, 13, 21] и определяется по выражению
.
(2.20)
Этот частный случай имеет наибольшее
практическое значение, поскольку реальный закон распределения времени восстановления
большинства электроэнергетических объектов (поток восстановлений) близок
к экспоненциальному [10, 14]. Используя свойства этого распределения, запишем
очень важную зависимость:
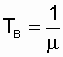
а также 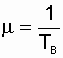
В дальнейшем эта взаимосвязь между
Тв и m
будет часто использоваться при анализе восстанавливаемых систем.
При более детальных расчетах показателей
надежности ремонтируемых (восстанавливаемых) объектов определяется такой
показатель ремонтопригодности, как процентное время восстановления g.
Это время в течение которого восстановление работоспособности объекта будет
осуществлено с вероятностью g
, выраженной в процентах [7].
2.4.
Комплексные показатели надежности
2.4.1.
Коэффициент готовности
Процесс функционирования восстанавливаемого
объекта можно представить как последовательность чередующихся интервалов
работоспособности и восстановления (простоя).
Коэффициент готовности – это вероятность
того, что объект окажется в работоспособном состоянии в произвольный момент
времени, кроме планируемых периодов, в течение которых применение объекта
по назначению не предусматривается [7]. Математическое определение этого
показателя дано ниже (разд. 7) при анализе надежности восстанавливаемых
систем.
Этот показатель одновременно оценивает
свойства работоспособности и ремонтопригодности объекта.
Для одного ремонтируемого объекта коэффициент
готовности
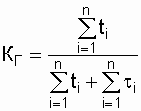
; 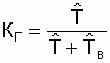
=
1. (2.23)
Из выражения 2.23 видно, что коэффициент
готовности объекта может быть повышен за счет увеличения наработки на отказ
и уменьшения среднего времени восстановления. Для определения коэффициента
готовности необходим достаточно длительный календарный срок функционирования
объекта.
Зависимость коэффициента готовности
от времени восстановления затрудняет оценку надежности объекта, так как
по КГ нельзя судить о времени непрерывной работы до отказа.
К примеру, для одного и того же численного значения КГ можно
иметь малые интервалы и
ti (см. рис. 2.4) и значительно большие. Таким образом можно
доказать, что на конкретном интервале работоспособности вероятность безотказной
работы будет больше там, где больше ti, хотя за этим интервалом
может последовать длительный интервал простоя .
Коэффициент готовности является удобной характеристикой для объектов, которые
предназначены для длительного функционирования, а решают поставленную задачу
в течение короткого промежутка времени (находятся в ждущем режиме), например,
релейная защита, контактная сеть (особенно при относительно малых размерах
движения), сложная контрольная аппаратура и т.д.
2.4.2.
Коэффициент оперативной готовности
Коэффициент оперативной готовности
КОГопределяется как вероятность того, что объект окажется в
работоспособном состоянии в произвольный момент времени (кроме планируемых
периодов, в течение которых применение объекта по назначению не предусматривается)
и, начиная с этого момента, будет работать безотказно в течение заданного
интервала времени.
Из вероятностного определения следует,
что
,
(2.23)
где КГ – коэффициент готовности;
Р(tр) – вероятность безотказной работы объекта в течение времени
(tр), необходимого для безотказного использования по назначению.
Для часто используемого в расчетной
практике простейшего потока отказов, когда
l =
w
,Р(tр) соответственно определяется по выражению
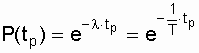
2.4.3.
Коэффициент технического использования
Коэффициент технического использования
КТИравен отношению математического ожидания суммарного времени
пребывания объекта в работоспособном состоянии за некоторый период эксплуатации
к математическому ожиданию суммарного времени пребывания объекта в работоспособном
состоянии и простоев, обусловленных техническим обслуживанием и ремонтом
за тот же период эксплуатации:
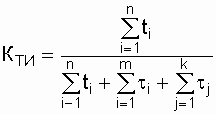
(2.25)
где ti – время сохранения
работоспособности в i-м цикле функционирования объекта; –
время восстановления (ремонта) после i-го отказа объекта; –
длительность выполнения j-й профилактики, требующей вывода объекта из работающего
состояния (использования по назначению); n – число рабочих циклов за рассматриваемый
период эксплуатации; m – число отказов (восстановлений) за рассматриваемый
период; k – число профилактик, требующих отключения объекта в рассматриваемый
период.
Как видно из выражения (2.25), коэффициент
технического использования характеризует долю времени нахождения объекта
в работоспособном состоянии относительно общей (календарной) продолжительности
эксплуатации. Следовательно, КТИотличается от КГтем,
что при его определении учитывается все время вынужденных простоев, тогда
как при определении КГвремя простоя, связанное с проведением
профилактических работ, не учитывается.
Суммарное время вынужденного простоя
объекта обычно включает время:
- – на поиск и устранение отказа;
-
– на регулировку и настройку объекта после
устранения отказа; -
– для простоя из-за отсутствия запасных
элементов; - – для профилактических работ.
В электроэнергетических объектах, к примеру,
в трансформаторах, линиях электропередачи, шинах распределительных устройств
и т.п., предусмотрены плановые отключения для проведения плановых ремонтов
и технического обслуживания. Эти интервалы времени так же как и интервалы,
связанные с отключением по причине отказа, учитываются при определении
анализируемых коэффициентов надежности.
В условиях эксплуатации на уровень
надежности объектов большое влияние оказывают техническое обслуживание
и ремонт. Подробно техническое обслуживание и ремонт, стратегии их организации
и их решающее влияние на надежность рассматриваются в [1, 16].
ГОСТ 27.002-89 содержит кроме проанализированных
в
данном пособии наиболее употребляемых
показателей надежности и другие показатели: среднюю трудоемкость восстановления,
средний срок сохраняемости, гамма-процентный ресурс, гамма-процентное время
восстановления, гамма-процентный срок сохраняемости и др. При необходимости
определения указанных показателей используются специальные методики, где
процедура расчета основывается на тех же законах математической статистики
и теории вероятностей, по которым определяются и более широко используемые
показатели надежности.
3.
ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ, НАИБОЛЕЕ ЧАСТО ИСПОЛЬЗУЕМЫЕ
В РАСЧЕТАХ НАДЕЖНОСТИ
3.1.
Распределение Вейбулла
Опыт эксплуатации очень многих электронных
приборов и значительного количества электромеханической аппаратуры показывает,
что для них характерны три вида зависимостей интенсивности отказов от времени
(рис. 3.1), соответствующих трем периодам жизни этих устройств [3, 8, 10,
19].
Нетрудно увидеть, что этот рисунок
аналогичен рис. 2.3, так как график функции l
(t) соответствует закону Вейбулла. Указанные три вида зависимостей интенсивности
отказов от времени можно получить, используя для вероятностного описания
случайной наработки до отказа двухпараметрическое распределение Вейбулла
[12, 13, 15]. Согласно этому распределению плотность вероятности момента
отказа
,
(3.1)
где d
– параметр формы (определяется подбором в результате обработки экспериментальных
данных, d > 0); l
– параметр масштаба,
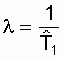
Интенсивность отказов определяется
по выражению
(3.2)
Вероятность безотказной работы
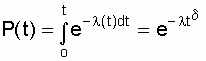
(3.3)
а средняя наработки до отказа
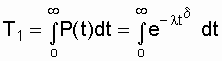
(3.4)
Отметим, что при параметре d=
1 распределение Вейбулла переходит в экспоненциальное, а при d=
2 – в распределение Рэлея.
При d<1
интенсивность отказов монотонно убывает (период приработки), а при монотонно
возрастает (период износа), см. рис. 3.1. Следовательно, путем подбора
параметра d можно
получить, на каждом из трех участков, такую теоретическую кривую l
(t), которая достаточно близко совпадает с экспериментальной кривой, и
тогда расчет требуемых показателей надежности можно производить на основе
известной закономерности.
Распределение Вейбулла достаточно близко
подходит для ряда механических объектов (к примеру, шарикоподшипников),
оно может быть использовано при ускоренных испытаниях объектов в форсированном
режиме [12].
3.2.
Экспоненциальное распределение
Как было отмечено в подразд. 3.1 экспоненциальное
распределение вероятности безотказной работы является частным случаем распределения
Вейбулла, когда параметр формы d
= 1. Это распределение однопараметрическое, то есть для записи расчетного
выражения достаточно одного параметра l
= const . Для этого закона верно и обратное утверждение: если интенсивность
отказов постоянна, то вероятность безотказной работы как функция времени
подчиняется экспоненциальному закону:
.
(3.5)
Среднее время безотказной работы при
экспоненциальном законе распределения интервала безотказной работы выражается
формулой:
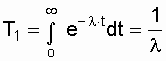
(3.6)
Заменив в выражении (3.5)
величину
l величиной
1 / Т1, получим 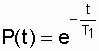
(3.7)
Таким образом, зная среднее время безотказной
работы Т1 (или постоянную интенсивность отказов l
), можно в случае экспоненциального распределения найти вероятность безотказной
работы для интервала времени от момента включения объекта до любого заданного
момента t.
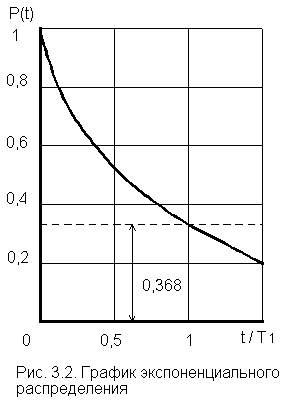
Отметим, что вероятность безотказной
работы на интервале, превышающем среднее время Т1, при экспоненциальном
распределении будет менее 0,368:
Р(Т1)
==
0,368 (рис. 3.2).
Длительность периода нормальной эксплуатации
до наступления старения может оказаться существенно меньше Т1,
то есть интервал времени на котором допустимо пользование экспоненциальной
моделью, часто бывает меньшим среднего времени безотказной работы, вычисленного
для этой модели. Это легко обосновать, воспользовавшись дисперсией времени
безотказной работы. Как известно [4, 13], если для случайной величины t
задана плотность вероятности f(t) и определено среднее значение (математическое
ожидание) Т1, то дисперсия времени безотказной работы находится
по выражению:
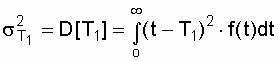
и для экспоненциального распределения
соответственно равна:
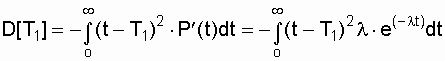
(3.9)
После некоторых преобразований получим:
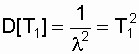
(3.10)
-
Таким образом, наиболее вероятные значения
наработки, группирующиеся в окрестности Т1, лежат в диапазоне,
то есть в диапазоне от t = 0 до t = 2Т1. Как видим, объект может
отработать и малый отрезок времени и время -
t = 2Т1, сохранив l
= const. Но вероятность безотказной работы на интервале 2Т1
крайне
низка:
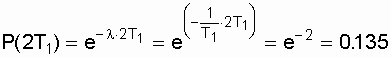
Важно отметить, что если объект отработал
предположим, время t
без отказа, сохранив l
= соnst, то дальнейшее распределение времени безотказной работы будет таким,
как в момент первого включения l
= соnst.
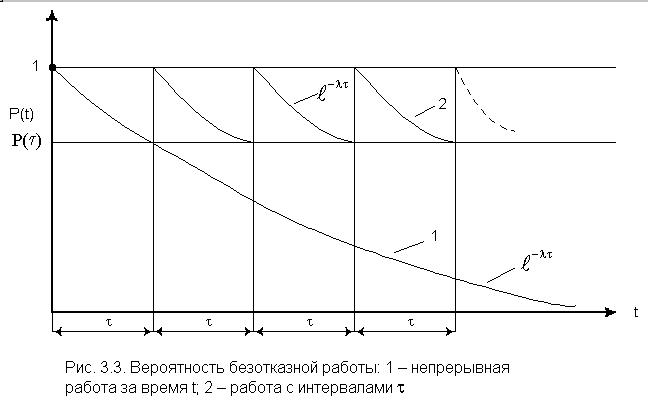
Таким образом, отключение работоспособного
объекта в конце интервала и
новое его включение на такой же интервал множество раз приведет к пилообразной
кривой (см. рис. 3.3).
Другие распределения не имеют указанного
свойства. Из рассмотренного следует на первый взгляд парадоксальный вывод:
поскольку за все время t устройство не стареет (не меняет своих свойств),
то нецелесообразно проводить профилактику или замену устройств для предупреждения
внезапных отказов, подчиняющихся экспоненциальному закону. Конечно, никакой
парадоксальности этот вывод не содержит, так как предположение об экспоненциальном
распределении интервала безотказной работы означает, что устройство не
стареет. С другой стороны, очевидно, что чем больше время, на которое включается
устройство, тем больше всевозможных случайных причин, которые могут вызвать
отказ устройства. Это весьма важно для эксплуатации устройств, когда приходится
выбирать интервалы, через которые следует производить профилактические
работы с тем, чтобы сохранить высокую надежность работы устройства. Этот
вопрос подробно рассматривается в работе [1].
Модель экспоненциального распределения
часто используется для априорного анализа, так как позволяет не очень сложными
расчетами получить простые соотношения для различных вариантов создаваемой
системы. На стадии апостериорного анализа (опытных данных) должна проводиться
проверка соответствия экспоненциальной модели результатам испытаний. В
частности, если при обработке результатов испытаний окажется, что ,
то это является доказательством экспоненциальности анализируемой зависимости.
На практике часто бывает, что l№const,однако,
и в этом случае его можно применять для ограниченных отрезков времени.
Это допущение оправдывается тем, что при ограниченном периоде времени переменную
интенсивность отказов без большой ошибки можно заменить [12, 15] средним
значением:
l (t) “lcр(t)
= const.
3.3.
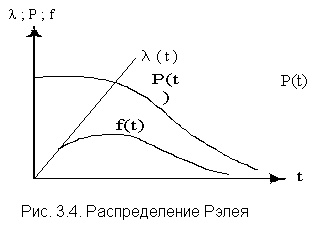
Распределение Рэлея
Плотность вероятности в законе Рэлея
(см. рис. 3.4) имеет следующий вид
¦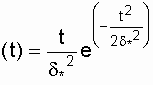
(3.11)
где d*
– параметр распределения Рэлея (равен моде этого распределения [13]). Его
не нужно смешивать со среднеквадратическим отклонением:
.
Интенсивность отказов равна:
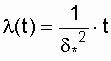
Характерным признаком распределения
Рэлея является прямая линия графика l(t),
начинающаяся с начала координат.
Вероятность безотказной работы объекта
в этом случае определится по выражению
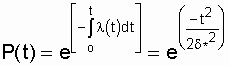
(3.12)
Средняя наработка до отказа
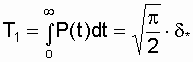
(3.13)
3.4.
Нормальное распределение (распределение Гаусса)
Нормальный закон распределения характеризуется
плотностью вероятности вида
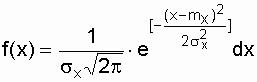
(3.14)
где mx,
sx
– соответственно математическое ожидание и среднеквадратическое отклонение
случайной величины х.
При анализе надежности электроустановок
в виде случайной величины, кроме времени, часто выступают значения тока,
электрического напряжения и других аргументов. Нормальный закон – это двухпараметрический
закон, для записи которого нужно знать mx и sx.
Вероятность безотказной работы определяется
по формуле
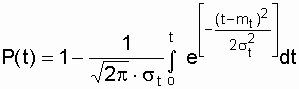
(3.15)
а интенсивность отказов – по формуле
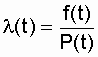
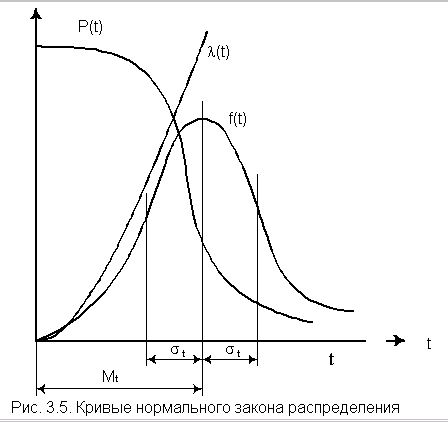
На рис. 3.5 изображены кривые l(t),
Р(t) и¦ (t) для случая
st<<
mt, характерного для элементов, используемых в системах автоматического
управления [3].
В данном пособии показаны только наиболее
распространенные законы распределения случайной величины. Известен целый
ряд законов, так же используемых в расчетах надежности [4, 9, 11, 13, 15,
21]: гамма-распределение, -распределение,
распределение Максвелла, Эрланга и др.
Следует отметить, что если неравенство
st<<
mt не соблюдается, то следует использовать усеченное нормальное
распределение [19].
Для обоснованного выбора типа практического
распределения наработки до отказа необходимо большое количество отказов
с объяснением физических процессов, происходящих в объектах перед отказом.
В высоконадежных элементах электроустановок,
во время эксплуатации или испытаний на надежность, отказывает лишь незначительная
часть первоначально имеющихся объектов. Поэтому значение числовых характеристик,
найденное в результате обработки опытных данных, сильно зависит от типа
предполагаемого распределения наработки до отказа. Как показано в [13,15],
при различных законах наработки до отказа, значения средней наработки до
отказа, вычисленные по одним и тем же исходным данным, могут отличаться
в сотни раз. Поэтому вопросу выбора теоретической модели распределения
наработки до отказа необходимо уделять особое внимание с соответствующим
доказательством приближения теоретического и экспериментального распределений
(см. разд. 8).
3.5.
Примеры использования законов распределения в расчетах надежности
Определим показатели надежности для
наиболее часто используемых законов распределения времени возникновения
отказов.
3.5.1.
Определение показателей надежности при экспоненциальном законе распределения
Пример. Пусть объект
имеет экспоненциальное распределение времени возникновения отказов с интенсивностью
отказов l = 2,5 Ч
10-5 1/ч.
Требуется вычислить основные показатели
надежности невосстанавливаемого объекта за t = 2000 ч.
Решение.
-
Вероятность безотказной работы за время
t = 2000 ч равна - Вероятность отказа за t = 2000 ч равна
q (2000)
= 1 – Р (2000) = 1 – 0,9512 = 0,0488.
-
Используя выражение (2.5), вероятность
безотказной работы в интервале времени от 500 ч до 2500 ч при условии,
что объект проработал безотказно 500 ч равна
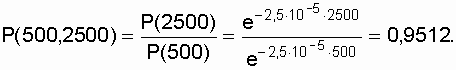
- Средняя наработка до отказа
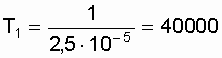
3.5.2.
Определение показателей надежности при распределении Рэлея
Пример. Параметр распределения d*
= 100 ч.
Требуется определить для t = 50 ч величины
P(t), Q(t), l (t),Т1.
Решение.
Воспользовавшись формулами (3.11),
(3.12), (3.13), получим
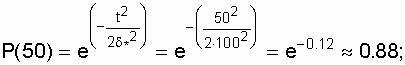
;
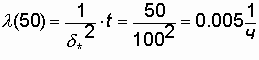
3.5.3.
Определение показателей схемы при распределении Гаусса
Пример. Электрическая схема собрана
из трех последовательно включенных типовых резисторов: ;
(в
% задано значение отклонения сопротивлений от номинального).
Требуется определить суммарное сопротивление
схемы с учетом отклонений параметров резисторов.
Решение.
Известно, что при массовом производстве
однотипных элементов плотность распределения их параметров подчиняется
нормальному закону [15]. Используя правило 3s
(трех сигм), определим по исходным данным диапазоны, в которых лежат значения
сопротивлений резисторов: ;
Следовательно,
Когда значения параметров элементов
имеют нормальное распределение, и элементы при создании схемы выбираются
случайным образом, результирующее значение Rеявляется
функциональной переменной, распределенной так же по нормальному закону
[12, 15], причем дисперсия результирующего значения, в нашем случае ,
определяется по выражению
.
Поскольку результирующее значение Rераспределено
по нормальному закону, то, воспользовавшись правилом 3s
, запишем
,
где –
номинальные паспортные параметры резисторов.
Таким образом
,
или
.
Данный пример показывает, что при увеличении
количества последовательно соединенных элементов результирующая погрешность
уменьшается. В частности, если суммарная погрешность всех отдельных элементов
равна ± 600 Ом, то
суммарная результирующая погрешность равна ±
374 Ом. В более сложных схемах, например в колебательных контурах, состоящих
из индуктивностей и емкостей, отклонение индуктивности или емкости от заданных
параметров сопряжено с изменением резонансной частоты, и возможный диапазон
ее изменения можно предусмотреть методом, аналогичным с расчетом резисторов
[15].
3.5.4.
Пример определения показателей надежности неремонтируемого объекта по опытным
данным
Пример. На испытании находилось Nо
= 1000 образцов однотипной невосстанавливаемой аппаратуры, отказы фиксировались
через каждые 100 часов.
Требуется определить в
интервале времени от 0 до 1500 часов. Число отказов на
соответствующем интервале представлено
в табл. 3.1.
Таблица 3.1
Исходные данные и результаты расчетов
|
|
|
|
|
| 1 | 0 -100 | 50 | 0,950 |
|
| 2 | 100 -200 | 40 | 0,910 | 0,430 |
| 3 | 200 -300 | 32 | 0,878 | 0,358 |
| 4 | 300 – 400 | 25 | 0,853 | 0,284 |
| 5 | 400 – 500 | 20 | 0,833 | 0,238 |
| 6 | 500 – 600 | 17 | 0,816 | 0,206 |
| 7 | 600 -700 | 16 | 0,800 | 0,198 |
| 8 | 700 – 800 | 16 | 0,784 | 0,202 |
| 9 | 800 – 900 | 15 | 0,769 | 0,193 |
| 10 | 900 -1000 | 14 | 0,755 | 0,184 |
| 11 | 1000 -1100 | 15 | 0,740 | 0,200 |
| 12 | 1100 -1200 | 14 | 0,726 | 0,191 |
| 13 | 1200 -1300 | 14 | 0,712 | 0,195 |
| 14 | 1300 -1400 | 13 | 0,699 | 0,184 |
| 15 | 1400 -1500 | 14 | 0,685 |
0,202 Ч |
Решение.
Согласно формуле (2.1) для любого отрезка
времени, отсчитываемого от t = 0,
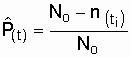
– по формуле Гаусса
где ti – время от начала
испытаний до момента, когда зафиксировано n(ti) отказов.
Подставляя исходные данные из табл.
3.1, получим:
Воспользовавшись формулой (2.9), получим
значение , 1/ч:
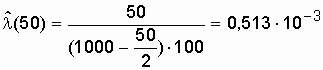
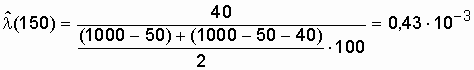
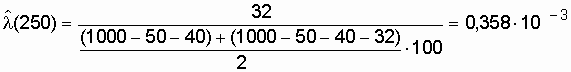
…………………………………………………………………………………………………..
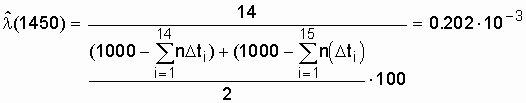
Средняя наработка до отказа, при условии
отказов всех No объектов, определяется по выражению
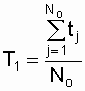
-
где tj – время отказа j-го объекта ( j
принимает значения от 0 до Nо). -
В данном эксперименте из Nо
=
1000 объектам отказало всегообъектов.
Поэтому по полученным опытным данным можно найти только приближенное значение
средней наработки до отказа. В соответствии с поставленной задачей воспользуемся
формулой из [13]:
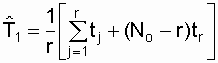
r
Ј
Nо , (3.16)
где tj – наработка до отказа j-го объекта
( j принимает значения
от 1 до r);
r – количество зафиксированных
отказов (в нашем случае r = 315);
tr – наработка до r-го (последнего) отказа.
Полагаем, что последний отказ зафиксирован
в момент окончания эксперимента (tr = 1500).
На основе экспериментальных данных
суммарная наработка объектов до отказа равна
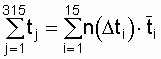
где –
среднее время наработки до отказа объектов, отказавших на интервале .
В результате
ч.
Примечание: обоснование расчетов ,
по ограниченному объему опытных данных, изложено в разд. 8.
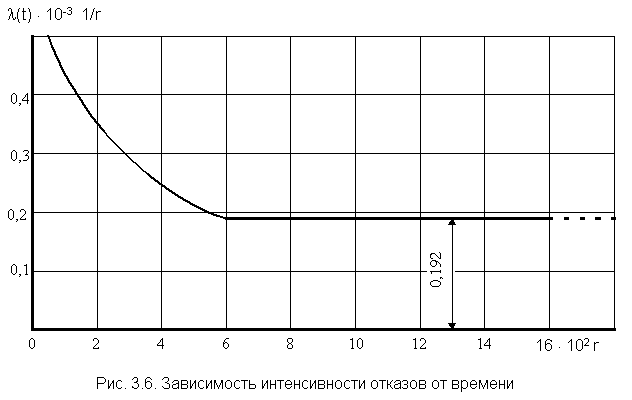
По полученным данным (см. табл. 3.1)
построим график l(t).
Из графика видно, что после периода
приработки t і 600
ч интенсивность отказов приобретает постоянную величину. Если предположить,
что и в дальнейшем l
будет постоянной, то период нормальной эксплуатации связан с экспоненциальной
моделью наработки до отказа испытанного типа объектов. Тогда средняя наработка
до отказа
ч.
Таким образом, из двух оценок средней
наработки до отказа
=
3831 ч и T1 = 5208 ч надо выбрать ту, которая более соответствует
фактическому распределению отказов. В данном случае можно предполагать,
что если бы провести испытания до отказа всех объектов, то есть r =
Nо,
достроить график рис. 3.6 и выявить время, когда l
начнет увеличиваться, то для интервала нормальной эксплуатации (l
= const) следует брать среднюю наработку до отказа T1 = 5208
ч.
В заключение по данному примеру отметим,
что определение средней наработки до отказа по формуле (2.7), когда r <<
Nо, дает грубую ошибку. В нашем примере
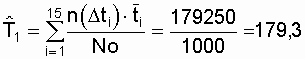
Если вместо Nо поставим
количество отказавших объектов
r = 315, то получим
ч.
В последнем случае не отказавшие за
время испытания объекты в количестве Nо –
r = 1000-315 = 685
шт. вообще в оценку не попали, то есть была определена средняя наработка
до отказа только 315 объектов. Эти ошибки достаточно распространены в практических
расчетах.
ВВЕРХ
Для компаний стало критически важным измерять и отслеживать эффективность предоставления услуг в быстро меняющемся цифровом мире. Однако, когда программное обеспечение для управления инцидентами измеряет различные показатели и отслеживает время безотказной работы и время простоя, небольшой сбой в системе может нарушить бизнес-процессы, что обходится в миллионы долларов.
MTTR, MTBF, MTTF и MTTA — это сокращения некоторых наиболее важных показателей управления инцидентами. В области Управление ИТ-услугами, эти аббревиатуры помогают организациям планировать свои ресурсы, чтобы гарантировать, что они могут позаботиться о проблемах, вызванных сбоями аппаратного и программного обеспечения. Полные формы следующие:
- Среднее время ремонта
- Среднее время между сбоями
- Среднее время до отказа
- Среднее время подтверждения
Давайте углубимся в каждую метрику.
Среднее время восстановления (MTTR) – это среднее время, необходимое для восстановления системы и восстановления ее полной функциональности. Расчет MTTR начинается после начала ремонта и продолжается до полного восстановления нарушенных служб, включая любое необходимое время тестирования.
В сфере управления ИТ-услугами буква R в слове MTTR не всегда означает ремонт. Это также может означать восстановление, ответ или решение. Хотя все эти показатели соответствуют друг другу, они имеют свои собственные значения, поэтому всегда рекомендуется уточнять, какой MTTR следует использовать. Кратко рассмотрим, что означает каждый из них.
- Среднее время восстановления (MTTR) – это среднее время, необходимое для восстановления после поломки устройства или системы. Это охватывает весь процесс от отключения из-за простоя до момента, когда система снова станет полностью работоспособной. MTTR – хороший индикатор для измерения скорости общего процесса восстановления.
- Среднее время ответа (MTTR) – это среднее время, необходимое для восстановления после сбоя системы с момента получения первого предупреждения о сбое, не включая задержку в системе предупреждений. Этот MTTR обычно используется в сфере кибербезопасности для измерения эффективности команды в отражении системных атак.
- Среднее время решения (MTTR) представляет собой среднее время, затрачиваемое на полное устранение неисправности системы, включая время, необходимое для обнаружения неисправности, диагностики проблемы и решения проблемы, убедившись, что неисправность больше не повторится. Этот показатель MTTR в основном используется для измерения процесса разрешения непредвиденных инцидентов, а не запросов на обслуживание.
Как вы рассчитываете MTTR?
Поскольку MTTR – это показатель управления инцидентами, который ИТ-команды используют для отслеживания ремонта, предприятиям следует стремиться к тому, чтобы значение MTTR было как можно ниже. Это достижимо за счет повышения производительности бригад, выполняющих ремонтные работы. MTTR можно рассчитать следующим образом:
MTTR = общее время, затраченное на ремонт в течение заданного периода/количество ремонтов
Предположим, что в системе было 6 сбоев, и обслуживание, необходимое для восстановления системы до полной функциональности, заняло 3 часа, что составляет 180 минут. Итак, MTTR будет,
MTTR = 180/6 = 30 минут
Это означает, что MTTR организации составляет 30 минут, то есть время, которое в среднем организация тратит на каждый простой.
Ускорьте цифровую трансформацию с помощью службы поддержки Motadata с поддержкой искусственного интеллекта, которая помогает сократить MTTR примерно на 80%. Хотите узнать больше? Свяжитесь с нашим экспертным отделом продаж по адресу sales@motadata.com or Попробуйте 30 бесплатных пробных версий сегодня.
Что такое среднее время наработки на отказ (MTBF)?
Среднее время наработки на отказ (MTBF) – это среднее время, прошедшее между ремонтируемым отказом оборудования и его следующим возникновением. Среднее время безотказной работы измеряет доступность и надежность, поэтому чем выше значение MTBF, тем надежнее система.
Среднее время безотказной работы – это показатель, который помогает клиентам принимать обоснованные решения о том, когда обновлять систему или вводить оборудование в эксплуатацию. Если после фазы профилактического обслуживания среднее время безотказной работы улучшилось, это говорит о повышении надежности оборудования. Увеличение MTBF также демонстрирует эффективность процессов обслуживания.
Как вы рассчитываете MTBF?
MTBF – это время, прошедшее от одного отказа до следующего. Математически это можно рассчитать следующим образом:
Среднее время безотказной работы = общее время безотказной работы между отказами / общее количество отказов
Предположим, система отлично работает 13 часов. В течение этого периода произошло 3 отказа, в результате чего общее время простоя составило 1 час. Итак, MTBF будет,
Среднее время безотказной работы = (13-1) / 3 = 4 часа
Эта цифра означает, что сбой в системе происходит каждые 4 часа, что приводит к отключению системы и убыткам для организации. Отслеживание этого показателя может помочь спланировать стратегии, которые могут сократить время простоя.
Поскольку MTBF используется для отслеживания надежности, оно отражает только непредвиденные простои и не учитывает возможные простои во время планового обслуживания.
Как мы упоминали ранее, MTBF используется для отслеживания отказов в ремонтируемых системах. Для отслеживания отказов, требующих замены системы, используется показатель, называемый «Среднее время до отказа» (MTTF).
Что такое среднее время до отказа (MTTF)?
Средняя наработка до отказа (MTTF) – это среднее время, прошедшее между неисправимыми отказами оборудования. MTTF измеряет надежность неремонтопригодных систем и показывает время, в течение которого система, как ожидается, будет функционировать до полного отказа.
MTTF – важный показатель, используемый для измерения срока службы заменяемого или неремонтопригодного оборудования, такого как клавиатуры, батареи, настольные телефоны, мыши и т. Д. Исторические данные о MTTF каждого типа оборудования позволяют ИТ-специалистам поэтапно планировать устаревание.
Поскольку метрика используется для определения того, как долго обычно прослужит система, определение того, превосходит ли новая версия системы старую, также поможет понять ожидаемый срок службы и время планирования проверок системы.
Как вы рассчитываете MTTF?
Среднее время безотказной работы является основным показателем надежности оборудования, не подлежащего ремонту, поэтому цель состоит в том, чтобы увеличить срок службы актива. Более короткий MTTF приводит к частым простоям и сбоям. Для расчета MTTF используйте следующую формулу:
MTTF = общее количество часов работы / общее количество отказов
Предполагая, что мы должны исследовать три идентичные системы, пока все они не откажутся. Первая система проработала 14 часов, вторая – 16 часов, а третья – 12 часов. MTTF в этом случае будет,
MTTF = (14 + 16 + 12) / 3 = 14 часов.
Это означает, что данный тип системы в среднем необходимо заменять каждые 14 часов, чтобы предотвратить более длительные простои и последующие повреждения.
Что такое среднее время подтверждения (MTTA)?
Среднее время подтверждения (MTTA) — это среднее время, необходимое организации для ответа на жалобы, сбои или инциденты во всех отделах. Метрика управления инцидентами MTTA используется для отслеживания реакции группы поддержки и эффективности системы оповещения.
Медленное реагирование может снизить эффективность сотрудников, когда внутренние системы сталкиваются с проблемами и стоит организациям денег. Отслеживая и минимизируя MTTA, организации могут оптимизировать свои процессы, повысить удовлетворенность клиентов и увеличить прибыль.
Как вы рассчитываете MTTA?
MTTA – полезная мера для контроля скорости отклика. Если команда слишком долго отвечает и страдает от усталости от предупреждений, этот показатель поможет выявить проблему. Для расчета MTTA используйте следующее математическое представление:
MTTA = общее время, прошедшее между предупреждением и подтверждением / общее количество инцидентов
Допустим, в организации произошло 5 инцидентов, и между предупреждением и подтверждением для всех инцидентов прошло в общей сложности 30 минут, тогда MTTA будет
MTTA = 30/5 = 6 минут
Это означает, что MTTA для организации составляет 6 минут, и организация должна работать над сокращением этого времени, чтобы оптимизировать процесс разрешения проблем.
Заключение
Подводя итог, можно сказать, что среднее время восстановления (MTTR) – это мера, с помощью которой вы можете увидеть, как быстро вы можете вернуть неисправное оборудование в рабочее состояние. Среднее время наработки на отказ (MTBF) дает вам представление о том, насколько эффективна ваша группа поддержки в минимизации или предотвращении надвигающихся инцидентов. Используя метрическую среднюю наработку до отказа (MTTF), вы можете определить срок службы системы или оборудования. Наконец, среднее время для подтверждения (MTTA) – ценный показатель, с помощью которого вы можете отслеживать реакцию вашей группы ИТ-поддержки.
Теперь, когда вы понимаете эти метрики инцидентов в деталях, вы поймете, что каждая метрика предлагает разные точки зрения. При одновременном использовании эти мощные показатели могут дать более глубокое представление о том, как ваша группа поддержки управляет перебоями в обслуживании, и помочь вам снизить потери из-за неэффективности и проблем с качеством. Чтобы узнать больше о том, какие другие показатели управления услугами вы должны отслеживать, прочитайте нашу статью 7 важных показателей службы поддержки для измерения.
Избавьтесь от проблем, вызванных сбоями аппаратного и программного обеспечения, с помощью унифицированного решения Motadata для управления ИТ-инцидентами ServiceOps. Повышайте рентабельность инвестиций за счет сокращения количества ошибок. Хотите узнать больше о наших решениях? Контакты прямо сейчас
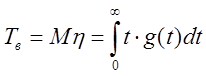 ,
,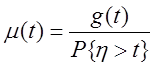
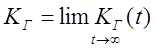
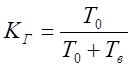 ,
,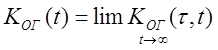 .
.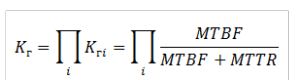
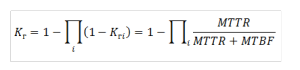


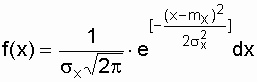
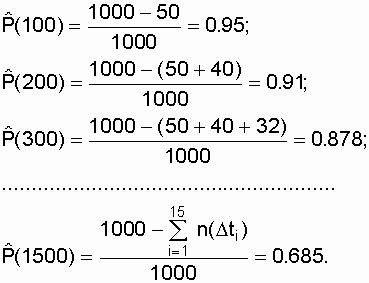
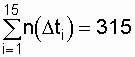 объектов.
объектов.