Как найти среднее значение амплитуды

Под
средним
значением,
синусоидально изменяющейся величины
понимают ее среднее значение за
полпериода. Так, среднее значение тока

(3.4)

т.
е. среднее значение синусоидального
тока составляет 2/=
0,638 от амплитудного. Аналогично, Е_ср=2Е_т/;
U_ср=2U_m/.

Широко применяют
понятие действующего значения
синусоидально изменяющейся величины
(его называют также эффективным или
средне­квадратичным). Действующее
значение тока

(3.5)

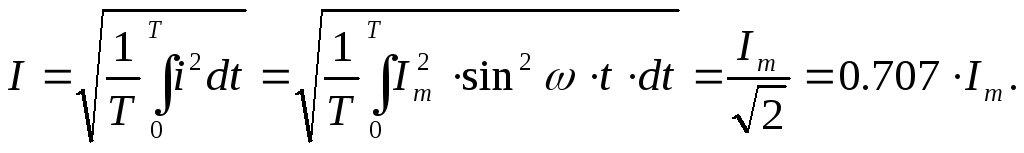
Следовательно,
действующее значение синусоидального
тока равно 0,707 от амплитуды. Аналогично,

Можно
сопоставить тепловое действие
синусоидального тока с теп­ловым
действием постоянного тока , текущего
то же время по тому же сопротивлению.

Количество теплоты,
выделенное за один период синусоидальным
током,

Выделенная
за то же время постоянным током теплота
равна R
I²
_пост
T.
Приравняем их:

или

Таким
образом, действующее
значение
синусоидального тока I
численно равно значению такого постоянного
тока, который за время, равное периоду
синусоидального тока, выделяет такое
же количество теплоты, что и синусоидальный
ток.

Большинство
измерительных приборов показывает
действующее значение измеряемой величины
.

3.3. Коэффициент амплитуды и коэффициент формы.

Коэффи­циент
амплитуды k_a
— это
отношение амплитуды периодически
изменяющейся функции к ее действующему
значению.

Так,
для синусоидального тока

(3.6)

Под
коэффициентом формы k_Ф
понимают от­ношение действующего
значения периодически изменяющейся
функции к ее среднему за пол­периода
значению. Для синусоидального тока

(3.7)

Иногда
пользуются понятием коэффициента формы
несинусоидаль­ной функции, определенного
следующим образом:

по модулю

где
I_ср
–среднее
по модулю
значение тока.

3.4. Изображение синусоидально изменяющихся величин векто­рами на комплексной плоскости. Комплексная амплитуда. Комплекс действующего значения.

На
рис. дана комплексная плоскость, на
которой можно изобразить комплексные
числа. Комплексное число имеет
действительную (вещественную) и мнимую
части. По оси абсцисс комплексной
плоскости откладывают действительную
часть комплекс­ного числа, а по оси
ординат—мнимую часть. На оси действительных
значений ставим +1. а на оси мнимых
значений
.

И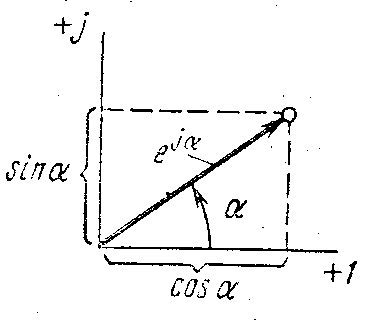з
курса математики известна формула
Эйлера

(3.8)

Комплексное
число e
^ja
изображают на комплексной плоскости
вектором, численно равным единице и
составляющим угол к с осью вещественных
значений (осью +1). Угол а
отсчитываем против часо­вой стрелки
от оси + 1. Модуль функции

П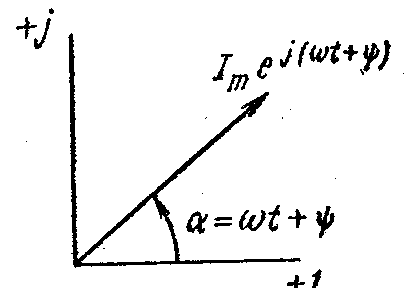роекция
функцииe
^ja
на ось +1 равна cos
a,
а на ось +j
равна sin
а. Если вместо
функции e
^ja
взять функцию Im
e
^ja,
то

I_m
e
^ja=I_mcosa+jI_msina.

На
комплексной плоскости эта функция, так
же как и функция e
^ja,
изобразится под углом a
к оси

+
1, но величина вектора будет в I_m
раз больше.

Угол
a
в формуле (3.8) может быть любым. Положим,
что a=t+
изменяется прямо пропорционально
времени. Тогда

I_me
^{j(t+)}=I_mcos(t+)+jI_msin(t+).
(3.9)

Слагаемое
I_mcos(t+)
представляет
собой действительную часть (Re)
выражения I_me
^{j(t+)}

I_mcos(t+)=Re
I_me^{j(t+)}
(3.10)

а
функция
I_msin(t+)
есть
коэффициент при мнимой части (Im)
выражения I_me^{j(t+)}

i=
I_msin(t+)=Im
I_me^{j(t+)}

(3.10a)

Таким
образом синусоидально изменяющийся
ток i
ср.
(3.1) и (3.10а)
можно представить как Im
I_me
^{j(t+)}
или, что то
же самое, как проекцию вращаю­щегося
вектора I_me
^{j(t+)}на
ось +j
(рис.3.3).

Исторически
сложилось так, что в радиотехниче­ской
литературе за основу обычно принимают
не сину­соиду, а косинусоиду и потому
пользуются формулой (3.10).

С
целью единообразия принято на комплекс­ной
плоскости изображать векторы синусоидально
изменяющихся во времени величин
для момента времени t=0.
При этом вектор равен

I_me
^{j(t+)}=
I_me
^j=İ_m
,
(3.11)

где
İ_m
— комплексная величина, модуль которой
равен I_m;

– угол, под которым вектор İ_m
проведен к оси + 1 на комплексной
плоскости, равен начальной фазе .

Величину
1_т
называют комплексной
амплитудой
тока i.
Комп­лексная амплитуда изображает
ток i
на комплексной плоскости для момента
времени t=0.

Рассмотрим
два числовых примера на переход от
мгновенного значения тока к комплексной
амплитуде и от комплексной амплитуды
и мгновенному значению.

Соседние файлы в папке Новая папка

• #

  12.04.2015140.29 Кб21выключRC.avi

• #

  12.04.2015134.66 Кб22выключRL.avi

• #
• #
• #
• #
• #
• #
• #
• #
• #

The largest deviation of a variable from its mean value is referred to as amplitude. It is the largest displacement from a particle’s mean location in to and fro motion around a mean position. Periodic pressure variations, periodic current or voltage variations, periodic variations in electric or magnetic fields, and so on all have amplitudes.

Amplitude does not have a specific formula. It can be obtained by equations or graphical representations of such variations.

What is an Amplitude?

The highest displacement of the waves is referred to as amplitude. In addition, you will learn about amplitude, amplitude formula, formula derivation, and a solved example in this course. Furthermore, you will be able to comprehend amplitude after completing the topic.

Amplitude refers to the greatest deviation from equilibrium that an item in periodic motion might display. A pendulum, for example, swings past its equilibrium point (straight down) before reaching its maximum distance from the centre.

Furthermore, the amplitude’s distance is A. Furthermore, the pendulum’s complete range has a magnitude of 2A. Waves and springs, for example, follow a periodic motion. Furthermore, because the sine function oscillates between +1 and -1, it may be used to depict periodic motion.

SI Unit: The metre is the most notable amplitude unit (m).

Formula for Amplitude

The amplitude of a variable is the biggest variation from its mean value. The amplitude formula can be used to calculate the sine and cosine functions. Amplitude is represented by the letter A. The sine (or cosine) function has the following formula:

x = A sin (ωt + ϕ)   

or   

x = A cos (ωt + ϕ)

where,

• x = displacement of wave (meter)
• A = amplitude
• ω = angular frequency (rad/s)
• t = time period
• ϕ = phase angle

The amplitude formula is also known as the average of the maximum and minimum values of a sine or cosine function. The absolute amplitude value is always used.

Sample Problems

Problem 1: Consider a pendulum that swings back and forth. In addition, the phase shift is 0 radians. Furthermore, the pendulum is 14.0 cm or x = 0.140 m, and the time is t = 8.50 s. So, what is the oscillation’s amplitude?

Solution:

Given that,

x = 0.140 m

ω = π radians/s

ϕ = 0

t = 8.50 s

So, we can find the value of amplitude by rearranging the formula:

x = A sin (ωt+ϕ) → A = xsin(ωt+ϕ)

A = xsin(ωt+ϕ)

So, A = 0.14msin[(πradians/s)(8.50s)+0]

A = 0.140msin(8.50π)

Moreover, the sine of 8.50 π can be solved (by keeping in mind that the values is in radians) with a calculator:

Sin(8.50 π) = 1

So, the amplitude at time t is 8.50s is:

A = 0.140msin(8.50π)

A = 0.140m1

A = 0.140 m

Therefore, the amplitude of the pendulum’s oscillation is A =0.140 m = 14.0 cm.

Problem 2: Assume a spring is bouncing the head of a jack-in-the-box toy upward and downward. In addition, the oscillation’s angular frequency is π/6 radians/s, with a phase shift (ϕ) of 0 radians. The bouncing also has a 5.00 cm amplitude. Where does the Jack-in-the-head stand in relation to the equilibrium position in 6 s?

Solution:

Since, as we know that:

x = A sin (ωt+ϕ)

x = (0.500 m) sin [(π/6radians/s)(6.00s) + 0]

x = (0.500 m) sin (π/6radians/s)

x = (0.500 m) (0.00)

x = 0.00 m

So, at time t =6.00 s, the head of the-jack-in-the-box is at position 0.00 m that is the equilibrium position.

Problem 3: If y = 6 cos (7t + 1) is a wave. Find its amplitude.

Solution:

Given: equation of wave y = 6cos(7t + 1)

Using amplitude formula,

x= A cos (ωt + ϕ)

On comparing it with the wave equation:

A = 6

ω = 7

ϕ = 1

Therefore, the amplitude of the wave = 6 units. 

Problem 4: A wave is y = 2sin(4t). Find out its amplitude.

Solution:

The wave equation y = 2sin(4t)

Using the formula for amplitude,

x = A sin(ωt + ϕ)

When comparing the wave equation to the equation of motion,

A = 2

ω = 4

ϕ = 0

As a result, the amplitude of the wave is 2 units.

Problem 5: Consider a jack-in-the-box toy with its head bouncing up and down on a spring. Furthermore, the oscillation’s angular frequency is = π/6radians/s, and the phase shift is ϕ= 0 radians. Furthermore, the bouncing has a 5.00 cm amplitude. So, where does the Jack-in-the-head stand in relation to the equilibrium position in 1s.

Answer:

x = A sin (ωt+ϕ)

x = (0.500 m) sin [(π/6radians/s)(1.00s) + 0]

x = (0.500 m) sin (π/6radians/s)

x = (0.500 m) (0.500)

x = 0.250 m

x = 2.50 cm

So, at time 1.00 s the head of the jack-in-the-box is 2.5 cm above the equilibrium position.

Last Updated :
01 Feb, 2022

Like Article

Save Article

Переменный электрический ток

Переменный ток (AC – Alternating Current) – электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC – Direct Current – постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.

Величина тока будет равна квадратному корню из суммы квадратов двух величин – значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.

Термины AC и DC применимы как для тока, так и для напряжения.

Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.

Частота  f – величина, обратная периоду, равная количеству периодов за одну секунду.

Один период в секунду это один герц (1 Hz). Частота f = 1/T

Циклическая частота  ω – угловая частота, равная количеству периодов за 2π секунд.

ω = 2πf = 2π/T

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°

Начальная фаза  ψ – величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.

Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.

i = i(t);   u = u(t)

Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:

i = I_ampsin(ωt);   u = U_ampsin(ωt)

С учётом начальной фазы:

i = I_ampsin(ωt + ψ);   u = U_ampsin(ωt + ψ)

Здесь I_amp и U_amp – амплитудные значения тока и напряжения.

Амплитудное значение – максимальное по модулю мгновенное значение за период.

I_amp = max|i(t)|;   U_amp = max|u(t)|

Может быть положительным и отрицательным в зависимости от положения относительно нуля.

Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.

Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.

Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой I_amp (U_amp)
среднеквадратичное значение определится из расчёта:

---

Коэффициент амплитуды и коэффициент формы

---

Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже  простым графиком не отделаешься. Среднеквадратичное значение —  это значение постоянного напряжения, который, проходя через  нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение  обозначается так: RMS (rms) — root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

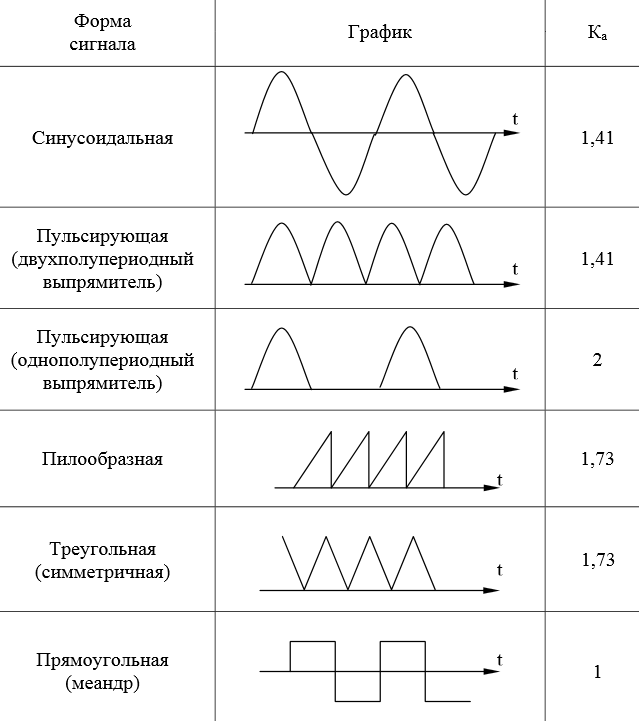
Вот некоторые значения коэффициента амплитуды K_a для некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.

Так вот, T-RMS  расшифровывается как True RMS —  «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».

Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

• Сред.  — средневыпрямленное значение сигнала. Это и есть площадь под кривой
• СКЗ — среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
• Пик. — амплитудное значение сигнала
• Пик-пик. — размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее  и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

• амплитуда,
• период,
• частота,
• циклическая частота,
• фаза,
• начальная фаза.

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

( large T left( c right) ) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» ( large nu ).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

( large nu left( frac{1}{c} right) ).

Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large  displaystyle frac{1}{c} = c^{-1} ).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

[ large boxed{ nu = frac{1}{T} }]

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

( large displaystyle omega left( frac{text{рад}}{c} right) )

Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».

Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:

[ large boxed{ omega = 2pi cdot nu }]

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.

Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).

И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).

(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.

Определим угол (large varphi_{0} ) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

• Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
• Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

[large T = 5 – 1 = 4 left( text{сек} right)]

Из графика следует, что период T = 4 сек.

• Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):

[large frac{Delta t }{T} = frac{1}{4} ]

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

• Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.

Для этого используем формулу:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )

Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.

• В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

[large varphi_{0} = — frac{pi }{2} ]

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».

Примечания:

1. Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
2. На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

Обозначим их:

( large varphi_{01}) – для первого процесса и,

( large varphi_{02}) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

[large boxed{ Delta varphi = varphi_{01} —  varphi_{02} }]

Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

• Связь между периодом, количеством колебаний и общим временем колебательного процесса:

[large boxed{ T cdot N = t }]

( large T left( c right) ) – время одного полного колебания (период колебаний);

( large N left( text{шт} right) ) – количество полных колебаний;

( large t left( c right) ) – общее время для нескольких колебаний;

• Период и частота колебаний связаны так:

[large boxed{ T = frac{1}{nu} }]

(large nu left( text{Гц} right) ) – частота колебаний.

• Количество и частота колебаний связаны формулой:

[large boxed{ N = nu cdot t}]

• Связь между частотой и циклической частотой колебаний:

[large boxed{ nu cdot 2pi = omega }]

(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.

• Фаза и циклическая частота колебаний связаны так:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

(large varphi_{0} left( text{рад} right) ) — начальная фаза;

(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;

• Между фазой и количеством колебаний связь описана так:

[large boxed{ varphi = N cdot 2pi }]

• Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.