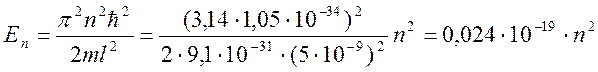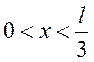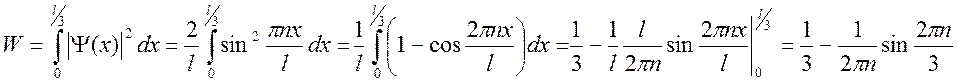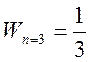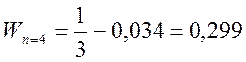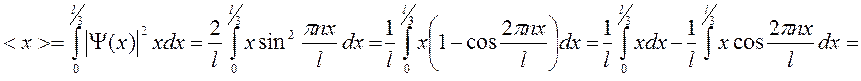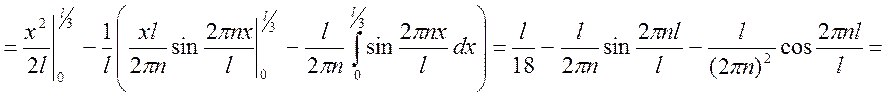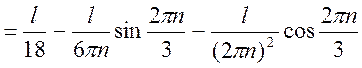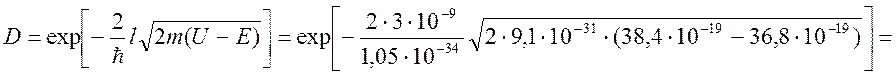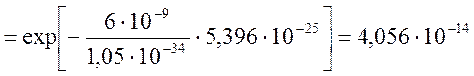Как найти среднее значение частицы

Лекция 8

Бесконечно
глубокая прямоугольная потенциальная
яма. Спектр, стационарные состояния,
разложения по собственным функциям
гамильтониана, средние

Пусть
потенциальная энергия частицы равна

(бесконечно
глубокая потенциальная яма шириной
,
см. рисунок). Найдем собственные значения
и собственные функции оператора
Гамильтона этой частицы.

Так
как в областях

потенциальная энергия обращается в
бесконечность, потребуем, чтобы при
этих значениях координат волновая
функция обращалась бы в нуль (в противном
случае средняя потенциальная энергия
частицы равнялась бы бесконечности).
Далее, так как согласно постулатам
квантовой механики волновая функция
непрерывна, то в точках

и

волновая функция также равна нулю.
Поэтому для нахождения волновых функций
и энергий стационарных состояний
необходимо решить уравнение

(1)

в
области

с граничными условиями

и
.

Как
было доказано на предыдущей лекции, все
собственные значения должны быть больше
минимального значения потенциала,
поэтому будем решать уравнение (1) при

.

Линейно
независимыми частными решениями
уравнения (1) при

являются функции

и
,
где
.
Поэтому общее решение уравнения (1) имеет
вид

(2)

Из
граничного условия при

находим
.
Из второго граничного условия получаем

,
то есть либо
,
либо

,

.
(3)

Первое
условие приводит к нулевому решению.
Таким образом, ненулевые непрерывные
решения уравнения (1), удовлетворяющие
граничным условиям, существуют только
при значениях
,
при которых выполнено условие (3), из
которого находим

,

(5)

Энергии
(5) и являются собственными значениями
оператора Гамильтона и согласно
постулатам квантовой механики являются
возможными наблюдаемыми значениями
энергии частицы, находящейся в бесконечно
глубокой потенциальной яме. Собственной
функцией, отвечающей собственному
значению
,
является функция

(6)

где

Как
и должно быть, постоянная

осталась неопределенной. Она может быть
определена из условия нормировки. Легко
проверить, что функции

(7)

нормированы
на единицу. Отметим, что эти функции не
обладают определенной четностью,
несмотря на то, что
,
поскольку при значениях координат,
лежащих вне ямы, все собственные функции
равны нулю. Однако если бы яма была
расположена симметрично относительно
начала координат, то волновые функции
стационарных состояний обладали бы
определенной четностью. Действительно,
в этом случае собственные функции можно
получить из (7) с помощью сдвига их
аргумента на

Знание
спектра собственных значений и собственных
функций частицы в потенциальной яме
позволяет согласно постулатам квантовой
механики отвечать на вопросы о возможных
значениях энергии частицы в тех или
иных состояниях и их вероятностях.
Рассмотрим несколько примеров.

Пусть,
например, частица в яме в момент времени

имеет волновую функцию

(8)

(где

– постоянная). Что можно сказать о
результатах измерения энергии частицы
в момент времени
?
Какой будет средняя энергия частицы
как функция времени?

Согласно
основным принципам квантовой механики
для ответа на вопросы такого рода нужно
разложить волновую функцию частицы по
собственным функциям оператора
Гамильтона. Пользуясь известной
тригонометрической формулой, представим
начальную волновую функцию частицы в
виде

(9)

Формула
(9) представляет собой разложение
начальной волновой функции по собственным
функциям оператора Гамильтона, в котором,
таким образом, с равными весами
представлены только третья и тринадцатая
собственные функции; коэффициенты перед
остальными собственными функциями
равны нулю. Это значит, что измерения
энергии в момент времени

с равными вероятностями

дадут третье и тринадцатое

(10)

собственные
значения. Отсюда легко найти среднюю
энергию частицы в этот момент

(11)

Так
как гамильтониан не зависит от времени,
то вероятности различных значений
энергии и средняя энергия от времени
не зависят, и, следовательно, останутся
такими же в любой момент времени.

Можно решать и обратные задачи – т.е.
по результатам измерения энергий
восстанавливать волновую функцию, а по
ней находить вероятности возможных
значений различных наблюдаемых и их
средние значения. Например.

Энергия
частицы, находящейся в бесконечно
глубокой потенциальной яме, может
принимать два значения

и

(12)

с
вероятностями

и

соответственно. Будет ли среднее значение
координаты частицы

в этом состоянии зависеть от времени?

Будем рассуждать так. Поскольку
гамильтониан
частицы не зависит от времени, общее
решение временного уравнения Шредингера
имеет вид

(13)

где

и

– собственные значения и собственные
функции оператора Гамильтона,

– произвольные постоянные. Поскольку в
рассматриваемом состоянии энергия
частицы может принимать два значения

и
,
то в сумме (1) присутствуют два слагаемых,
отвечающие первому и третьему собственным
состояниям, а остальные коэффициенты

равны нулю. То есть волновая функция
частицы в любые моменты времени имеет
вид

(14)

где

,

.
(Отметим, что по данным условия волновая
функция восстанавливается неоднозначно,
поскольку не определяется фазовые
множители у коэффициентов

и
.
Тем не менее, эта неоднозначность не
помешает однозначно ответить на вопрос
задачи). Состояние (14) не является
стационарным, поэтому средние значения
физических величин в этом состоянии,
вообще говоря, зависят от времени.
Среднее значение координаты частицы в
состоянии (14) можно найти по
квантовомеханической формуле для
средних

(15)

(в
(15) использована действительность
собственных функций). Интегралы в первом
и втором слагаемом определяют среднее
значение координаты в первом и третьем
стационарных состояниях и, следовательно,
равны

(это утверждение проверяется с помощью
непосредственного вычисления интегралов
с использованием собственных функций

).
Так как волновые функции стационарных
состояний

и

четны относительно середины ямы и
ортогональны, то интегралы в третьем и
четвертом слагаемом равны нулю. Учитывая,
что
,
получим из (3)

(16)

То
есть среднее значение координаты в
данном нестационарном состоянии не
зависит от времени. Однако, если бы в
разложении начальной волновой функции
частицы по собственным функциям
гамильтониана содержались бы слагаемые,
отвечающие как четным, так и нечетным
стационарным состояниям, перекрестные
слагаемые в равенстве (15) не обращались
бы в нуль и среднее значение координаты
частицы зависело бы от времени.

Рассмотрим
еще один пример. Пусть волновая функция
частица в яме в момент времени

имеет вид

(17)

Какие
значения энергии можно получить при
измерениях?

Разложим
волновую функцию (17) по собственным
функциям Гамильтониана

(18)

где

– коэффициенты разложения, которые
согласно основным принципам квантовой
механики и определяют вероятности
различных значений энергии. Поскольку
собственные функции

– ортонормированны, коэффициенты

можно найти, умножая равенство (18) на
собственную функцию и интегрируя

(19)

Поскольку
волновая функция частицы – четна
относительно центра ямы (это парабола,
обращающаяся в нуль на границах ямы),
функции

– четны для нечетных номеров, и нечетны
для четных, то интеграл (19) будет отличен
от нуля только для нечетных номеров.
Следовательно, при измерении энергии
в рассматриваемом состоянии можно
обнаружить первое (отвечающее основному
состоянию), третье, пятое, седьмое и т.д.
собственные значения. Второе, четвертое,
шестое и т.д. собственные значения при
измерениях в рассматриваемом состоянии
невозможно.

6

Теоретическая часть

Определение физических величин

Для того, чтобы описать распределение вероятности нахождения
частицы в данный момент времени в некоторой точке пространства, вводят функцию , называемую волновой функцией.

Физический смысл имеет не сама функция , а квадрат ее модуля , где  –
функция, комплексно сопряженная с . Величина  имеет смысл плотности вероятности, т.
е. определяет вероятность пребывания частицы в данной точке пространства.

Функции , удовлетворяющие
уравнению Шредингера при данном значении U
(потенциальная энергия частицы в силовом поле), называются собственными
функциями. Значения Е (полной энергии частиц), при которых
существуют решения уравнения Шредингера, называются собственными значениями.

Уравнение Шредингера: .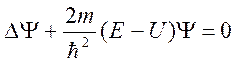

Отношение квантов модулей амплитуд отраженной и падающей
волн определяет вероятность отражения частицы от потенциального барьера и
называется коэффициентом отражения.

Отношение квантов модулей амплитуд прошедшей и падающей волн
определяет вероятность прохождения частицей потенциального барьера и называется
коэффициентом отражения.

Основные расчетные формулы

Собственное значение энергии
частицы: ,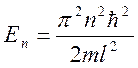

где       n – главное квантовое число, n = 1, 2, 3…;

             – постоянная Планка, ;

            m – масса электрона, ;

            l – ширина потенциальной ямы, м.

Волновая функция: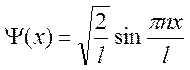, где х – координата частицы, м.

Вероятность пребывания частицы в
области (0, l): .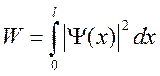

Среднее значение координаты частицы
в области (0, l): .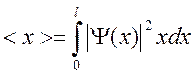

Коэффициент отражения (при ): ,

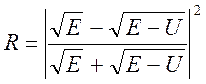
            где       Е –
энергия частицы, эВ.

                        U – высота потенциального барьера, эВ.

Коэффициент прозрачности (при ):,

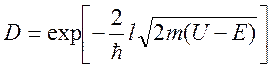
            где       l – ширина потенциального барьера, м.

Связь между R
и D:

Задание I

Исходные данные – Вариант №3:
; ; .

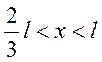
Электрон находится в потенциальной яме с бесконечно высокими
стенками и шириной l. При заданных n:

1)  построить
графики собственных функций;

2)  построить
графики плотности вероятности обнаружения частицы в интервале [0; l];

3)  найти
собственные значения энергии частицы. Изобразить схематически в удобном
масштабе энергетические уровни с указанием полученных значений энергии;

4)  найти
вероятность пребывания частицы в указанной области;

5)  найти среднее
значение координаты частицы в указанной области квантовой ямы.

1) 
Графики собственных функций              2)  Графики плотности
вероятности

 

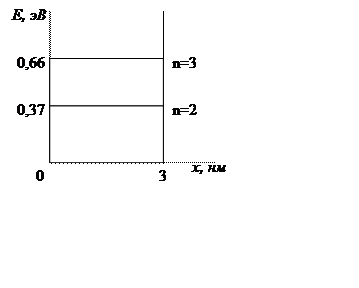
3)  Собственные значения энергии частицы

            Энергетические
уровни:

 

4)  Вероятность пребывания частицы в области

5)  Среднее значение координаты частицы в области

Анализ результатов

На каждом энергетическом уровне число полуволн соответствует
значению главного квантового числа.

Плотность вероятности представляет собой квадрат (по модулю)
волновой функции. Она не может иметь отрицательное значение.

Из пункта 3) можем видеть, что энергия частицы на четвертом
уровне почти в два раза больше, чем на третьем.

Так как на четвертом уровне в точке 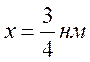 плотность
вероятности равна нулю, то уменьшается вероятность нахождения частицы в области
 по сравнению с третьим уровнем.

При расчете средней координаты можно было ожидать, что ее
значение будет находиться в пределах . Результаты
соответствуют этому. Причем на четвертом уровне средняя координата находится
левее, т. к. имеется нулевая плотность вероятности в точке .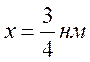

Задание II

Исходные данные – Вариант №3: ; ; .

Электрон с энергией Е проходит сквозь потенциальный
барьер высотой U. Определить вероятность:

1)  прохождения
частицы сквозь потенциальный барьер;

2)  отражения
частицы от потенциального барьера.

1)  Вероятность прохождения частицы сквозь барьер

Т. к. ,
то расчитываем D:

2)  Вероятность отражения частицы от барьера

Т. к. , то

.

Анализ результатов

Так как энергия частицы меньше потенциального барьера, то
вероятность ее отражения должна быть больше вероятности прохождения. Судя по
найденным коэффициентам, частица скорее всего отразится.

Основной целью компьютерного моделирования упаковок дискретных сред является получение статистически адекватных закономерностей, численно описывающих процесс структурообразования реальных сыпучих материалов. Следовательно, для построения компьютерной модели дискретной среды необходимо знать морфологические и размерные параметры частиц, из которых состоит дискретная среда.

В таблице 1 перечислены основные методы определения размеров частиц в зависимости от диапазона измеряемых частиц.

Таблица 1 – Экспериментальные методы определения размеров частиц в зависимости от диапазона измеряемых частиц

Результаты дисперсионных анализов могут быть изображены графически в виде интегральных и дифференциальных кривых распределения частиц по размерам. На гранулометрическом графике по оси абсцисс откладывается линейный размер (d) измеряемых частиц. В случае интегрального графика распределения (рисунок 1) размеров частиц по оси ординат откладываются объемные доли (Q) частиц, размер которых меньше текущего. Таким образом, интегральная кривая распределения представляет собой некую функцию Q=f(d).

Рисунок 1 – Интегральная кривая распределения частиц по размерам

Рисунок 2 – Разбивка интегральной кривой распределения размеров частиц на интервалы

Интервалы объемных долей можно представить в виде столбиков с высотой Fi=ΔQi, в таком случае мы получим дифференциальную гистограмму распределения частиц по размерам (рисунок 3).

Рисунок 3 – Дифференциальная гистограмма распределения частиц по размерам

Соединив середины верхних оснований столбиков дифференциальной гистограммы распределения, мы получим плавную дифференциальную кривую. Она означает, что частицы со средними размерами, заключенными между правым и левым краем одного столбика (diср), занимают Fi, % по объему в измеряемом материале.

Часто при построении дифференциальной кривой распределения, на оси ординат  откладывают  не  интервалы  объемных  долей  Fi,  а  отношения   ΔQi/Δdi. В полученной гистограмме площадь каждого прямоугольника представляет собой содержание фракции материала в пределах выбранного интервала размеров Δdi. Соединив плавной кривой середины верхних оснований прямоугольников, также получают дифференциальную кривую распределения, по которой можно определить dн.в. – наиболее вероятный диаметр частиц в данной дисперсной системе (рисунок 4).

Рисунок 4 – Дифференциальная кривая распределения частиц по размерам и наиболее вероятный диаметр частиц

Основными статистическими характеристиками дифференциальных кри-вых распределения частиц по размерам являются: среднее значение, медиана и мода распределения (рисунок 5).

Рисунок 5 – Основные статистические характеристики при нормальном или гауссовом распределении (а) и бимодальном распределении (б) частиц по размерам

Библиографические ссылки:

[1] – Роул, А. Основные принципы анализа размеров частиц / А. Роул // Техническая аннотация Malvern Instruments Limited. 2009. 12 c.