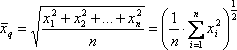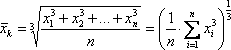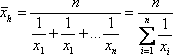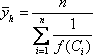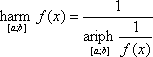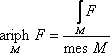Как найти среднее значение функции на отрезке

Пусть

интегрируема и ограничена на

и

,

— соответственно, верхняя и нижняя
грани

на отрезке

.
Тогда, существует такое число

,
что:

и

.

Число

называется средним значением функции

на отрезке

.

Примеры:

4.1. Вычислить
среднее значение функции

на отрезке

.

 По формуле
среднего значения функции на интервале,
получаем

.◄

4.2. Вычислить
среднее значение функции

на отрезке

.

 По формуле
среднего значения функции на интервале,
получаем

.◄

4.3. Вычислить
среднее значение функции

на отрезке

.

 По формуле
среднего значения функции на интервале,
получаем

.◄

5. Несобственные интегралы

5. 1. Интегралы с бесконечными пределами

Если

непрерывна на интервале

,
то интеграл

называется
несобственным интегралом от

.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если

при

,
то при

интеграл сходится, при

интеграл расходится.

Отметим важные
примеры несобственных интегралов:

– интеграл Пуассона,

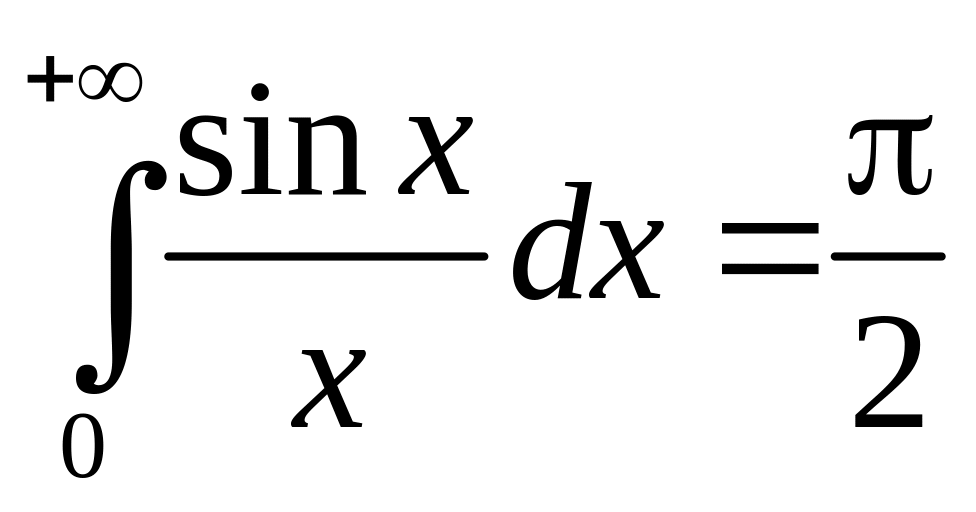
– интеграл Дирихле,

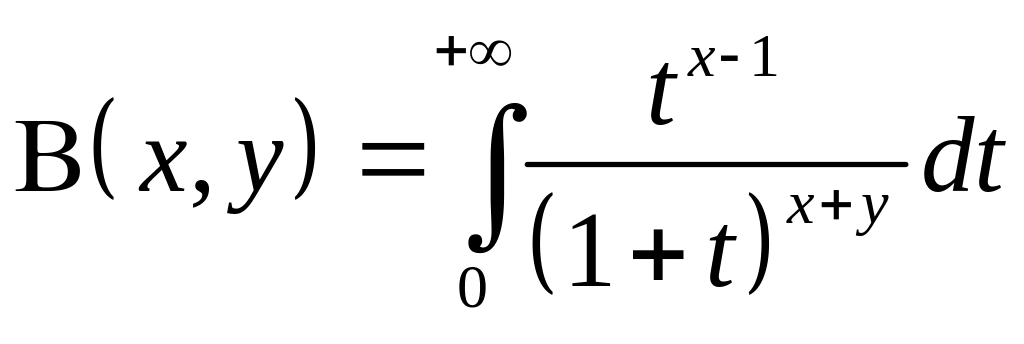
– Бета-функция
(эйлеров интеграл 1 рода),

– Гамма-функция
(эйлеров интеграл 2 рода).

Примеры:

5.1.1. Вычислить
интеграл

 Найдём

.

Предел существует
и конечен. Значит, интеграл сходится. ◄

5.1.2. Вычислить
интеграл

 Найдём

.

Предел не существует.
Несобственный интеграл расходится. ◄

5.1.3. Вычислить
интеграл
.

 Подынтегральная
функция чётная, поэтому

.

Вычислим интеграл:

.

Получили

.
Интеграл сходится. ◄

5.1.4. Доказать
расходимость интеграла
.

 Так как при

,

,
то вычисляя
интеграл

.

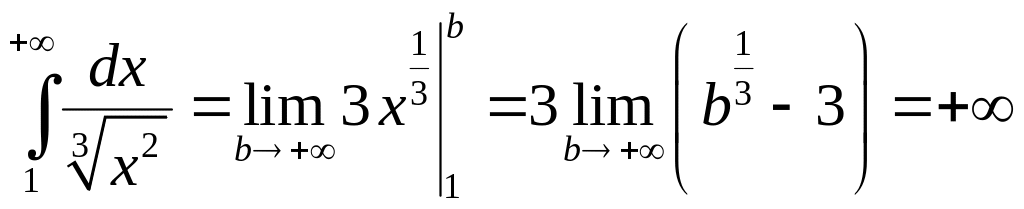
Этот интеграл
расходится. Следовательно, по признаку
сравнения исходный интеграл

тоже расходится.


5.2. Интегралы от функций с бесконечными разрывами

Если

непрерывна на

и неограниченна в любой окрестности
точки

,
то интеграл

называется
несобственным интегралом от

.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если

при

,
то при

интеграл сходится, при

интеграл расходится.

Примеры:

5.2.1. Исследовать
на сходимость интеграл
.

 Так как
подынтегральная функция

терпит
разрыв в точке

,
то получим:

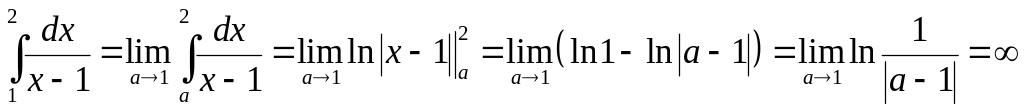
Конечного предела
не существует, значит, интеграл расходится.
◄

5.2.2.
Исследовать на сходимость интеграл

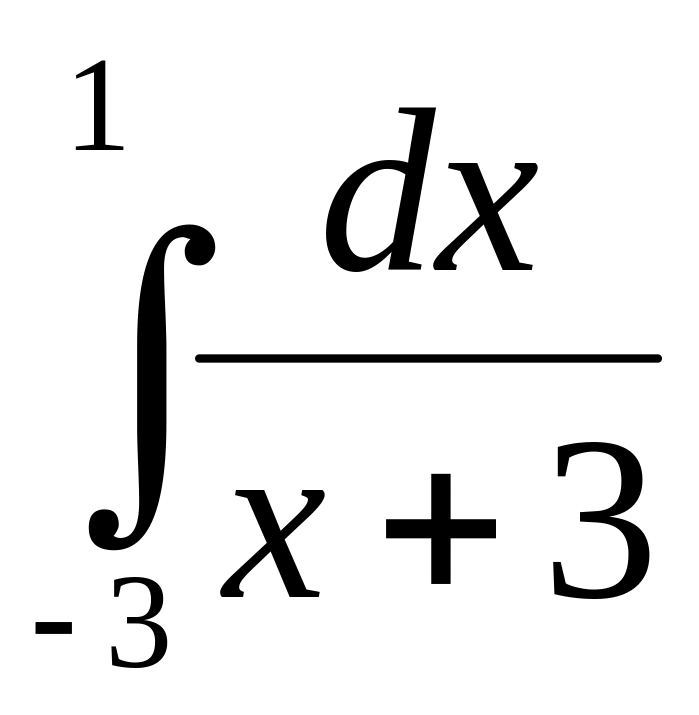
 Так как
подынтегральная функция

терпит
разрыв в точке

,
то получим:

.

Конечный предел
равен бесконечности. Значит, интеграл
расходится. ◄

5.2.3. Исследовать
на сходимость интеграл

 Так как
подынтегральная функция

терпит
разрыв в точке
,
получим:

.

Применим
интегрирование по частям. Пусть

Тогда

.

И первоначальный
интеграл примет вид:

.

Предел конечен.
Поэтому интеграл сходится.
◄

5.2.4. Исследовать
на сходимость интеграл

 Имеем

.

Предел бесконечен.
Следовательно, интеграл расходится.
◄

6. Геометрические и физические приложения определенного интеграла

6.1. Вычисление площади криволинейной трапеции

Площадь плоской
области

стандартной относительно оси

,
ограниченной прямыми

и

и кривыми

,

такими, что для любых

выполнено

(т.е.
)
вычисляется

.

Аналогично площадь
плоской области стандартной относительно
оси

,
ограниченной прямыми

и

и кривыми

,

такими, что для любых

выполнено

(т.е.
)
вычисляется

.

Если область

ограничена непрерывной замкнутой
кривой, заданной параметрически

,

то её площадь можно
вычислить по одной из трёх формул

,

,

.

Какую из них удобнее
применять, зависит от конкретного вида
функций

и

.

Площадь области

:

,

называемой
криволинейным сектором, ограниченной
графиком

и двумя лучами, составляющими с полярной
осью углы

и

имеет площадь

.

Примеры:

6.1.1.
Вычислить площадь области, ограниченной
линиями:

и

.

 Изобразим фигуру
в декартовой системе координат:

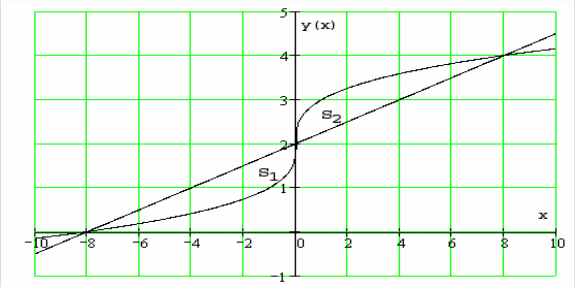
Из условия симметрии
фигуры относительно точки с координатами

,
площади

и

равны. Так как данная область является
стандартной как относительно оси

так и относительно оси

,
то ее площадь можно вычислить одним из
двух способов.

1) Выразим зависимости
в явном виде:

и
,

а стандартная
относительно оси

область

.

Тогда получаем

.

2) Заметим, что для
вычисления площади можно было
воспользоваться исходным видом
зависимостей:

.

6.1.2.
Вычислить площадь области, ограниченной
параболами

и

.

 Изобразим фигуру
в декартовой системе координат

Очевидно, область
симметрична относительно оси

,
кроме того, она не является стандартной
относительно оси

и стандартной относительно оси

,
а ее площадь можно вычислить одним из
двух способов.

1. Данная область
   не является стандартной относительно
   оси

   .
   Её можно разбить на две стандартные
   относительно оси

   области:

,

.

Из симметрии
областей

и

относительно оси

следует, что

.

1. Относительно оси

   данная область
   является стандартной:

.

Снова, используя
симметрию области, получаем

.

6.1.3.
Вычислить площадь эллипса, заданного
уравнением

(
,

).

 Искомую площадь
можно вычислить, используя как явное
представление линии, так и параметрическое.

1. Выразив уравнение
   в явном виде

,

получим,
применив подстановку

,

,
приходим к

.

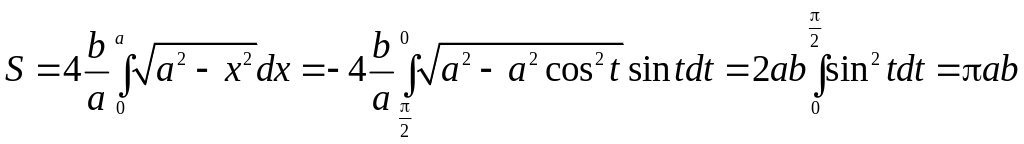
2) С другой стороны,
используя параметрическое представление

,

при изменении параметра

в пределах от

до

,
получаем:

.

6.1.4.
Вычислить площадь астроиды, заданной
уравнением

(
,
)

 Изобразим кривую
в декартовых координатах:

Используя
параметрическое представление

,

при изменении параметра

в пределах от

до

,
получаем:

.

6.1.5.
Найти площадь фигуры, ограниченной
кардиоидой

,

.

 Изобразим кривую
в декартовых координатах:

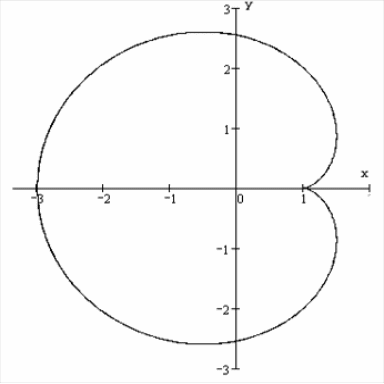
Так как кардиоида
симметрична относительно оси

,
то, используя параметрическое
представление, будем менять параметр

в пределах от

до

.
Так как

и
,

получаем по любой
из трех формул

,

,

.

Отметим, что площадь
кардиоиды задаваемой уравнением в
полярных координатах

равна

.

6.1.6.
Найти площадь области, ограниченной
кривой

.

 Кривая образует
три симметричные петли, каждая из которых
ограничивает криволинейный сектор.
Изобразим ее в полярных координатах.

Рассмотрим сектор,
лежащий в первой четверти:

.

Площадь его,
очевидно, равна 1/3 площади всей области,
ограниченной данной кривой. Следовательно,

.


Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как известно, среднее значение функции f(x), заданной на отрезке [a, b] равно:

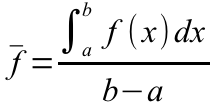
Но это только теория, вас же интересует скорее всего практическая сторона, а именно, вам задана какая-то конкретная функция и для неё необходимо найти среднее значение.

Лучше всего рассмотреть как получить среднее значение функции с помощью примера.

Например, вам дана функция:

f(x) = x*sin(x) и надо найти её среднее значение на отрезке [0, π/2]

Для того, чтобы найти ср. значение функции f(x) онлайн, надо воспользоваться тремя двумя шагами:

1. Получить подробное решение определённого интеграла (который стоит в числителе) здесь

Ввести, x*sin(x) как на рисунке ниже:

После этого нажать на кнопку “Найти интеграл”.

Тем самым вы вычислите числитель дроби, который входит в формулу для среднего значения функции.

В нашем примере это значение интеграла будет равно 1, значит числитель будет равен 1.

2. Вычисляем знаменатель. Он равен b — a = π/2 — 0 = π/2

3. Делим числитель на знаменатель и получим необходимое нам среднее значение функции:

22. Оценка интеграла. Теорема о среднем. Среднее значение функции

I. ОцеНКа интеграла. Укажем граНИцы, между которыми наверняка заключено значение интеграла.

Теорема VI (об оценке определенного интеграла). Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т. Е.

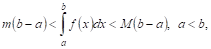
Где Т и М — Соответственно наименьшее и наибольшее значения функции 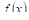интервале :

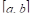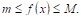
Доказательство. Возьмем две функци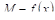и и 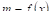. Первая из них в интервале 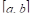неотрицательна, вторая неположительна. Значит, по теореме V

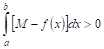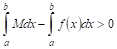и

и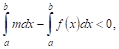

Откуда в силу того, что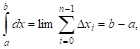

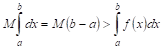
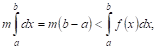
Что и требовалось доказать.

Геометрический смысл этих неравенств таков: площадь КриволиНейной трапеции больше площади прямоугольника с основанием, РавНой оснОваНИЮ трапеции, и высотой, равной наименьшей ординате ТрапециИ, и меньше площади прямоугольника с тем же основанием и Высотой, равной наибольшей ординате Трапеции (рис. 6).

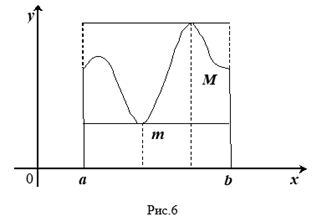
Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или дажЕ невозможно найти точное значение Интеграла, а оценивая его, мы узнаем, ХотЯ бы грубо, приближенное его Значение. С такого, рода оценками приходится Довольно часто встречаться в математике.

УказаННые в теореме VI границы для Интеграла тем более точны, чем короче Интервал интегрирования и чем меньше линия 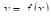отличается По положению от прямой, параллельной оси Ох.

Пример. Оценим интеграл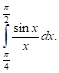

Легко проверить, что подынтегральная функция в интервале 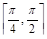убывает и, следовательно,

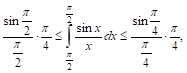
Т. е.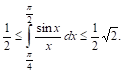

Таким образом, интеграл заключен между 0,5 и 0,71, что дает нам право считать его равным 0,6 с точностью до 0,1. Более точные приемы показывают, что приближенно он равен 0,62.

II. Обобщение теоремы об оценке интеграла. Интегрирование неравенств.

Справедлива следующая более общая теорема, чем теорема VI:

Теорема VII. Если в каждой точке Х интервала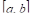

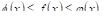
То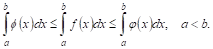

Это значит, что неравенство между функциями влечет неравенство того же смысла между их определенными интегралами, или, говоря коротко, Неравенства можно интегрировать..

На доказательстве и геометрическом смысле теоремы останавливаться не будем, так как они вполне подобны предыдущим.

В частном случае, когда 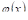тождественно равно М, а 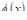тождественно равно Т, получаем теорему VI.

III. Теорема о среднем.

Определенный интеграл обладает следующим важным свойством:

Теорема VIII (о среднем). Внутри интервала интегрирования 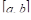существует, по меньшей мере, одно значение 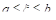для которого

. (*)

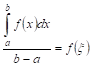Доказательство. В силу теоремы VI имеем:

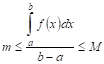
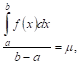
Где M — некоторое число, заключенное между наименьшим (Т) и наибольшим (М) значениями функции 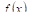в интервале 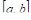, Т. Е. 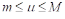. Но 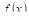, будучи непрерывной функцией, обязательно принимает, по меньшей мере, один раз каждое значение, лежащее между Т и М. Следовательно, при некотором 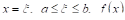получит значение, равное M, т. е. 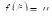(см. рис. 6), что и требовалось доказать.

Из равенства (*) находим:

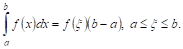
Эта формула позволяет теорему о среднем высказать в такой форме:

ОпредЕЛенный интеграл от непрерывной функции, равен произведению значения этой функции в некоторой промежуточной точке интервала интегрирования, на длину интервала.

Дадим наглядное пояснение теоремы. При движении прямой, параллельной оси Ох (рис. 6), вверх от положения ВС площадь прямоугольника АВСК будет непрерывно возрастать от величины, меньшей площади трапеции, до величины, большей ее. Очевидно, при некотором промежуточном положении прямой — обозначим его через FG — Площадь прямоугольника AFGK окажется в точности равной площади трапеции S. Так как при ЭТом движении прямая постоянно пересекает линию, ограничивающую трапецию, то и в положении FG найдется одна или несколько (на рис.

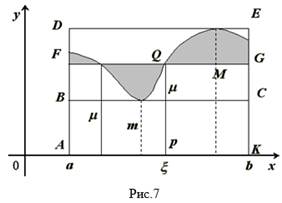
Точек пересечения Q; абсцисса любой точки пересечения и будет требуемым по теореме значением X.

Если трапецию ограничивает прямая линия, то 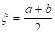; отрезок PQ будет при этом средней линией прямолинейной трапеции.

IV. Среднее арифметическое значение функции. Значение 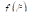, находимое по теореме о среднем, называется средним арифметическим значением функции 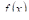в интервале .

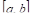Определение. Средним арифметическИМ значением 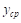непрерывной функции 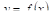в интервале 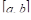называется отношение определенного интеграла от этой функции к длиНЕ интервала:

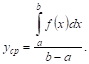
Приведем некоторые соображения в обоснование этого определения.

Пусть некоторая величина У принимает П значений: 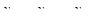Средним арифметическим значением этой величины называется частное 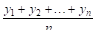. ТаК если температура воздуха в течение суток измеряется через каждый час, то средней температурой будет частное от деления суммы всех наблюденных температур на 24.

Но представим себе теперь, что величина изменяется непрерывно (например, температура воздуха известна в любой момент суток) и мы хотим как-то в среднем охарактеризовать всю совокупность ее значений. Как в этом случае следует определить среднюю температуру воздуха, принимая во внимание всю известную совокупность знАЧений температуры? Вообще, ЧтО следует принять в качестве среднего значения неПРерывной фуНКции 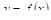в некотором интервале ?

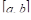Разобьем интервал 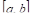на П равных частей с помощью точек 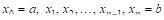и возьмем значения функции в этих N точках:

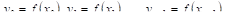
Значениями нашей функции во всех остальных точках интервала пока пренебрежем. Возьмем среднее арифметическое 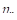указанных значений:

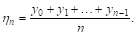
Ясно, что чем больше П, тем больше значений функции учитывается при отыскании среднего значения, и поэтому естественно за среднее значение 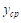функции принять предел, к которому стремится При . Найдем этот предел.

Умножив и разделив выражение для 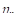на 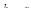, получим:

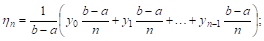
Но так как 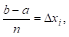То

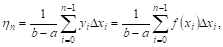
ОТкуда, переходя к пределу, получаем указанное нами выше выражение для среднего значения:

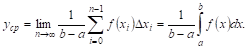
На основании теоремы о среднем (теорема VIII) мы заключаем, ЧТо 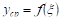, где 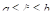, т. Е. что среднее значение непрерывной функции в интервале всегда (если только функция не постоянная) меньше некоторых ее значений, больше других ее значений и равно по меньшей мере одному ее значению.

Понятие среднего значения функции очень употребительно в техНИке. Многие величины часто характеризуются своими средними значениями; таковы, например, давление пара, сила и напряжение переменного тока, скорость химической реакции и т. п.

Среднее значение функции на отрезке

Здравствуйте!
Как найти среднее значение функции на отрезке? Может формулы есть?
Спасибо!

Рассмотрим вопрос о том, как находить среднее значение функции на отрезке.
По этому поводу существует теорема, которая называется теоремой о среднем. В ней говорится, что если на определенном отрезке заданная функция непрерывна, то на этом промежутке найдется такая точка, для которой будет выполняться условие:

Здесь a и b — концы отрезка, f(x) — заданная функция, а с — выше упоминаемая точка.
Значение функции в точке с называют средним ее значением на отрезке от а до b и находят по формуле:

Формулой очень удобно пользоваться, если функция на отрезке задана не линейная, а квадратичная, логарифмическая, тригонометрическая или какая-либо еще.
Рассмотрим пример.

Задание.
Найти среднее значение функции на отрезке [2; 13].

Решение.
Воспользуемся выше упомянутой формулой и подставим в нее известные значения:

Используем формулу Ньютона-Лейбница и найдем значение полученного выражения:

Упростим выражение и вычислим его результат:

Получили среднее значение функции на отрезке [2; 13] равным 35,8.

«Вы, профессор, воля ваша, что-то нескладное придумали! Оно, может, и умно, но больно непонятно. Над вами потешаться будут» «Мастер и Маргарита», Булгаков М. А.

Жизнь у всех разная и проявляется это ещё и в том, что источники информации, с которыми мы имеем дело, тоже у всех различны. Кроме этого, далеко не каждые сведения оставляют нас равнодушными, не вызывая совершенно никаких эмоций или мыслей. При этом иногда сочетание данных из двух источников может побуждать к весьма своеобразным умозаключениям.

Есть у меня одна книга – пособие для учителя информатики ^[1]. Не помню, как она у меня появилась – может купил, а может мне её кто-то подарил – однако в школе она мне как-то пригодилась в освоении языка Basic, программы на котором мы тогда собственноручно набивали на болгарских машинах «Правец 8A». Именно из этой книги я когда-то впервые узнал, что помимо так называемого среднего арифметического для нескольких чисел бывает, например, ещё и среднее квадратическое.

На первом курсе (1999-2000 гг.) университета, на лекциях по высшей математике, когда мы проходили определённые интегралы, была упомянута так называемая «теорема о среднем» ^{[2, с. 353]}. И вот это-то, в комбинации с сидящими в памяти сведениями из упомянутой книги, почему-то отозвалось в мозгах вопросом: «А какое именно среднее имеется в виду в теореме: арифметическое, кубическое или какое-нибудь другое?». Ну а раз возник вопрос – можно попытаться найти и ответ. Поиск сей вскоре привёл меня к тому, что, собственно, и составляет основу материала данной заметки. Свои измышления я условно назвал «теорией средних» и достаточно долгое время они хранились у меня в виде конспекта. Теперь же результаты этой «мозговой гимнастики» я выложил в сеть по следующим соображениям. Во-первых, если на этот материал наткнётся математик, то, думается, это сможет его повеселить. Во-вторых, мне слабо верится, что никто из профессиональных математиков в своих работах не додумался до чего-то подобному тому, что изложено здесь. В связи с этим мне особенно интересно было бы узнать, чьи это результаты мной, вероятно, «переоткрыты» – к сожалению, я не располагаю возможностью и временем это выяснить самостоятельно, но буду очень благодарен за сведения об этом.

---

I. Типы средних (введение)

Пусть у нас имеется множество из n чисел x₁, x₂,…x_n.

а) Среднее арифметическое этих чисел:

(1)

б) Среднее квадратическое:

(2)

в) Среднее кубическое:

(3)

г) Если ни одно из чисел рассматриваемого множества не равно нулю, то для них можно вычислить среднее гармоническое ^{[1, с. 132]}:

(4)

II. Средние значения функции на замкнутом числовом промежутке

Рассмотрим непрерывную функцию y=f(x), определённую на отрезке [a; b]. Разобьём [a; b] на n равных частей величиной Δx_i=(b–a)/n. Теперь внутри каждого отрезка разбиения Δx_i произвольно выберем точку C_i () и вычислим значение функции y=f(x) в точке C_i: y_i=f(C_i) (Рисунок 1).

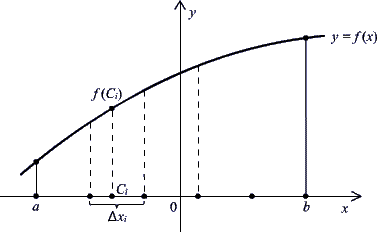
Рисунок 1.

Для полученного таким образом множества значений по формулам (1), (2), (3) можно вычислить средние арифметическое, квадратическое и кубическое:

В случае, если f(x) на [a; b] ни в одной точке не обращается в ноль, то по (4) можно вычислить и среднее гармоническое:

(8)

Будем теперь увеличивать неограниченно n и найдём пределы выражений (5), (6), (7) и (8) при n→∞. Если эти пределы существуют для рассматриваемой функции y=f(x) на отрезке [a; b], то назовём их, соответственно, средним арифметическим, средним квадратическим, средним кубическим и средним гармоническим значениями функции y=f(x) на отрезке [a; b]. Введём обозначения:

Для удобства операторы

, , ,

назовём арифией, квадрией, кубинией и гармонией соответственно.

III. Вычисление арифии функции на замкнутом числовом промежутке

Вернёмся к Рисунку 1. Составим для функции f(x) интегральную сумму Римана:

Эта сумма при неограниченном возрастании n имеет предел, равный интегралу:

Величина (b – a) – длина отрезка [a; b] – число постоянное, поэтому

(13)

Подставим (9) в (13):

или

(14)

Из (14) как раз и следует ответ на возникший у меня вопрос: в теореме о среднем фигурирует именно среднее арифметическое значение функции на отрезке (придуманная мной “арифия”).

IV. Свойства арифии функции на отрезке

Свойство 1 (свойство линейности оператора арифии):

(15)

(C₁ и C₂ – постоянные числа, f(x) и g(x) – непрерывные и определённые на [a; b] функции).

Доказательство:

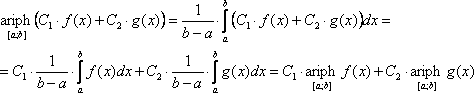
Свойство 2. Если C=const, то

(16)

Доказательство:

Свойство 3. Если a < c < b, то

(17)

Доказательство:

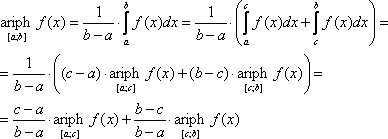
Свойство 4. Если f(x) – чётная функция и a > 0, то

(18)

Доказательство:

Так как f(x) – чётная, то

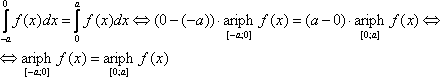
Далее:

,   .

Отсюда:

Свойство 5. Если f(x) – нечётная функция, то

	(19)
	(20)

Доказательство:

Так как f(x) – нечётная, то

,

отсюда

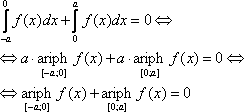
Свойство 6.

(21)

Доказательство:

Известно, что

Домножим обе части этого неравенства на (b – a) (b – a > 0):

V. Вычисление квадрии, кубинии и гармонии функции на отрезке

Пусть g₁(x)=[f(x)]², тогда

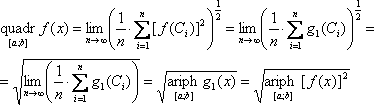
Итак:

(22)

Пусть теперь g₂(x)=[f(x)]³, тогда

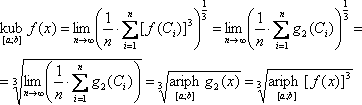
или

(23)

Пусть теперь функция y=f(x) на [a; b] ни в одной точке не принимает нулевого значения. Обозначим .

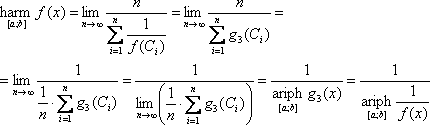
Окончательно:

(24)

VI. Свойства квадрии, кубинии и гармонии функции на отрезке

Свойство 7. Если C=const:

(25)

Доказательство:

Свойство 8.

(26)

Доказательство:

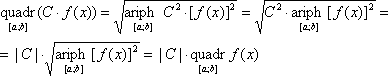
Аналогично доказываются следующие соотношения:

	(27)
	(28)

и (если C ≠ 0)

	(29)
	(30)

Свойство 9.

(31)

Доказательство:

Свойство 10.

(32)

Доказательство:

Из (22):

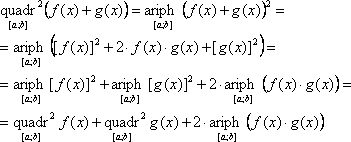
VII. Среднее значение функции нескольких переменных

По аналогии со средним значением функции на замкнутом числовом промежутке можно рассмотреть вопрос о среднем значении функции нескольких переменных в некоторой области значений её аргументов. Рассмотрим это на примере непрерывной функции двух независимых переменных z=f(x, y), определённой в некоторой области прямоугольной формы D. Разобьём эту область на k=n·m (n, m – целые числа) одинаковых площадок, внутри каждой из них произвольно выберем точку C_i () и вычислим значение функции z_i в каждой из них (Рисунок 2).

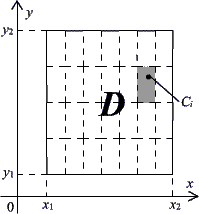
Рисунок 2.

Далее, по аналогии с (5) можно вычислить среднее полученных значений функции (например, среднее арифметическое):

(33)

Теперь можно начать неограниченно увеличивать n и m (и, соответственно, k) и найти предел выражения (33) при n → ∞, m → ∞ (k → ∞). Если этот предел существует для рассматриваемой функции, то его можно назвать средним арифметическим значением функции f(x, y) в области D. По аналогии с (9) можно ввести обозначение:

(34)

В соответствии с Рисунком 2 площадь каждого из k участков разбиения области D равна (S_D – площадь области D):

Составим для функции f(x, y) интегральную сумму Римана:

Эта сумма при неограниченном возрастании k имеет предел, равный следующему интегралу:

Так как S_D – число постоянное, то

Из полученного равенства следует формула для вычисления арифии функции двух переменных в области D:

(35)

Используя похожие рассуждения, можно также ввести определения для квадрии, кубинии и гармонии и получить формулы для их вычисления. Например:

(36)

Для функции трёх переменных t=f(x, y, z) формула для вычисления арифии в области v, имеющей форму прямоугольного параллелепипеда объёмом V_v, выглядит следующим образом:

(37)

При желании можно исследовать и свойства таких «средних». Так, оператор арифии обладает свойством линейности для функций одного, двух и трёх независимых переменных. Кроме этого, нетрудно заметить, что арифия во всех рассматриваемых случаях вычисляется сходным образом. Это позволяет написать условную обобщённую формулу для её вычисления: если мы имеем некоторую функцию F, то её среднее арифметическое значение в некоторой области M будет равно частному соответствующего интеграла функции по этой области и меры области (длины, площади или объёма):

(38)

---

В той книге по информатике была приведена ещё одна формула для среднего геометрического, определявшегося как корень степени n из произведения n чисел (надо полагать, неотрицательных). В принципе, ничто не мешает (с соответствующими оговорками и ограничениями) придумать «среднее геометрическое значение функции» и способ его вычисления (оно через логарифмирование фактически сводится к вычислению арифии логарифма исходной функции).

Литература:

[1]. Касаткин В.Н. Информация, алгоритмы, ЭВМ: Пособие для учителя. – М.: Просвещение, 1991. – 192 с.: ил.

[2]. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб.: в 2-х т. Т. 1 – СПб.: Мифрил. Гл. ред. Физ.-мат. лит., 1996. – 416 с.

Добавлено: 02.10.2011

Изменено: 02.10.2011

Скачать в pdf