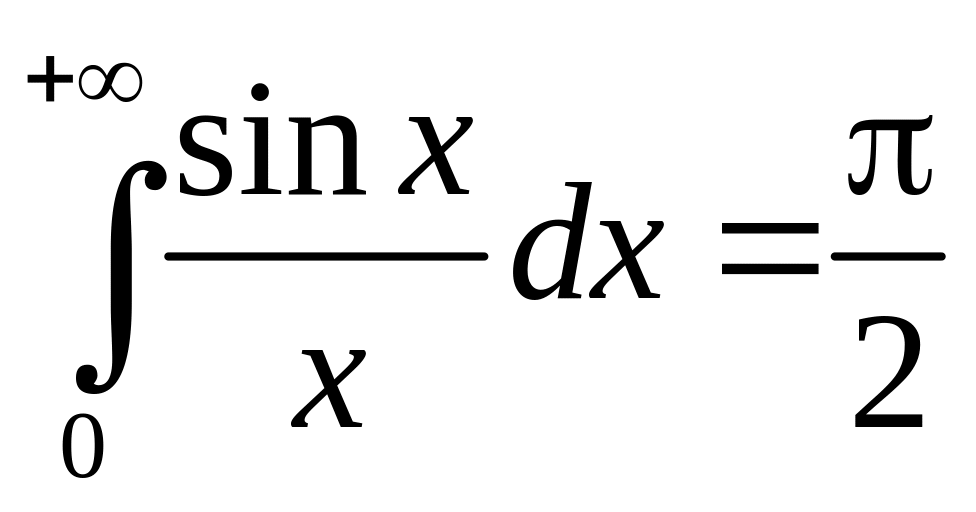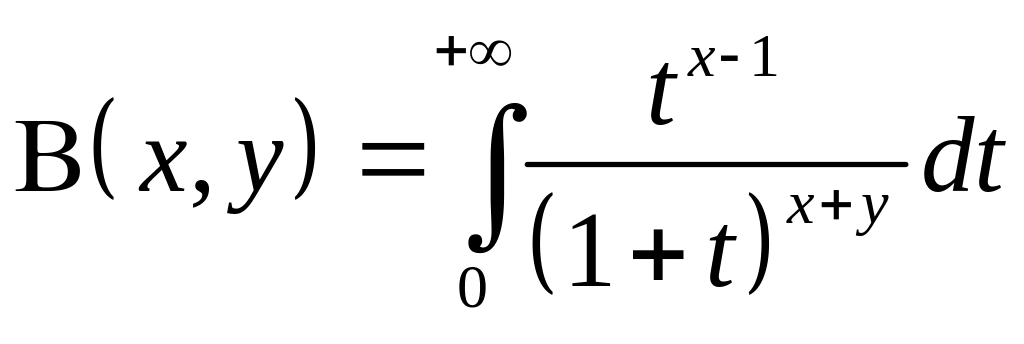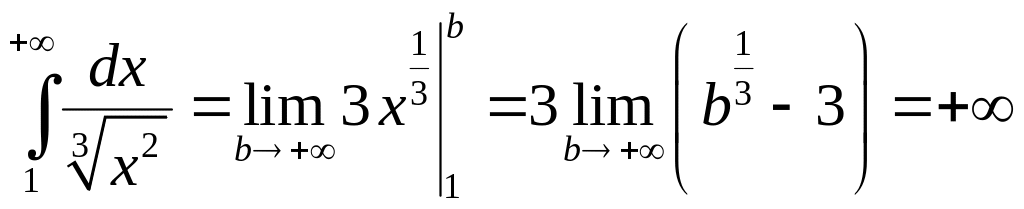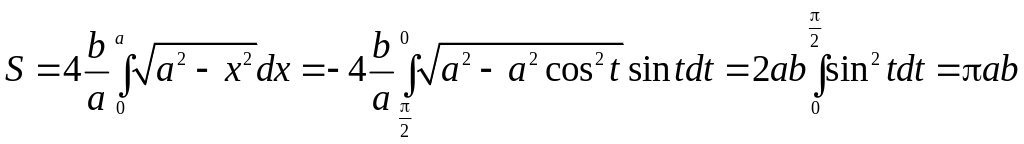Как найти среднее значение функции в области

Пусть

интегрируема и ограничена на

и

,

— соответственно, верхняя и нижняя
грани

на отрезке

.
Тогда, существует такое число

,
что:

и

.

Число

называется средним значением функции

на отрезке

.

Примеры:

4.1. Вычислить
среднее значение функции

на отрезке

.

 По формуле
среднего значения функции на интервале,
получаем

.◄

4.2. Вычислить
среднее значение функции

на отрезке

.

 По формуле
среднего значения функции на интервале,
получаем

.◄

4.3. Вычислить
среднее значение функции

на отрезке

.

 По формуле
среднего значения функции на интервале,
получаем

.◄

5. Несобственные интегралы

5. 1. Интегралы с бесконечными пределами

Если

непрерывна на интервале

,
то интеграл

называется
несобственным интегралом от

.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если

при

,
то при

интеграл сходится, при

интеграл расходится.

Отметим важные
примеры несобственных интегралов:

– интеграл Пуассона,

– интеграл Дирихле,

– Бета-функция
(эйлеров интеграл 1 рода),

– Гамма-функция
(эйлеров интеграл 2 рода).

Примеры:

5.1.1. Вычислить
интеграл

 Найдём

.

Предел существует
и конечен. Значит, интеграл сходится. ◄

5.1.2. Вычислить
интеграл

 Найдём

.

Предел не существует.
Несобственный интеграл расходится. ◄

5.1.3. Вычислить
интеграл
.

 Подынтегральная
функция чётная, поэтому

.

Вычислим интеграл:

.

Получили

.
Интеграл сходится. ◄

5.1.4. Доказать
расходимость интеграла
.

 Так как при

,

,
то вычисляя
интеграл

.

Этот интеграл
расходится. Следовательно, по признаку
сравнения исходный интеграл

тоже расходится.


5.2. Интегралы от функций с бесконечными разрывами

Если

непрерывна на

и неограниченна в любой окрестности
точки

,
то интеграл

называется
несобственным интегралом от

.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если

при

,
то при

интеграл сходится, при

интеграл расходится.

Примеры:

5.2.1. Исследовать
на сходимость интеграл
.

 Так как
подынтегральная функция

терпит
разрыв в точке

,
то получим:

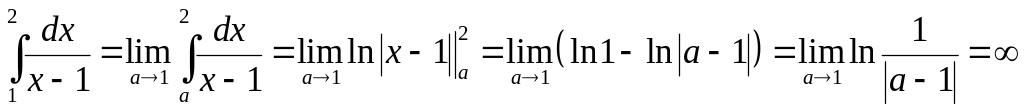
Конечного предела
не существует, значит, интеграл расходится.
◄

5.2.2.
Исследовать на сходимость интеграл

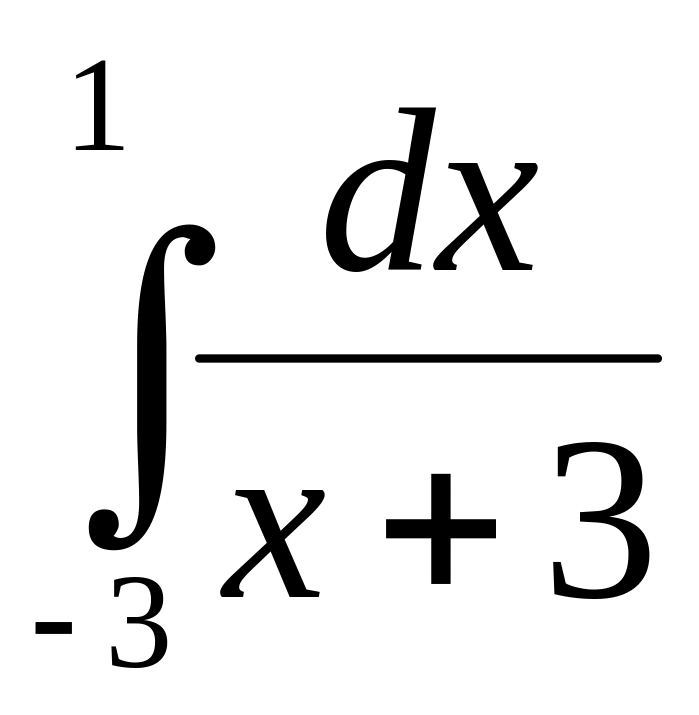
 Так как
подынтегральная функция

терпит
разрыв в точке

,
то получим:

.

Конечный предел
равен бесконечности. Значит, интеграл
расходится. ◄

5.2.3. Исследовать
на сходимость интеграл

 Так как
подынтегральная функция

терпит
разрыв в точке
,
получим:

.

Применим
интегрирование по частям. Пусть

Тогда

.

И первоначальный
интеграл примет вид:

.

Предел конечен.
Поэтому интеграл сходится.
◄

5.2.4. Исследовать
на сходимость интеграл

 Имеем

.

Предел бесконечен.
Следовательно, интеграл расходится.
◄

6. Геометрические и физические приложения определенного интеграла

6.1. Вычисление площади криволинейной трапеции

Площадь плоской
области

стандартной относительно оси

,
ограниченной прямыми

и

и кривыми

,

такими, что для любых

выполнено

(т.е.
)
вычисляется

.

Аналогично площадь
плоской области стандартной относительно
оси

,
ограниченной прямыми

и

и кривыми

,

такими, что для любых

выполнено

(т.е.
)
вычисляется

.

Если область

ограничена непрерывной замкнутой
кривой, заданной параметрически

,

то её площадь можно
вычислить по одной из трёх формул

,

,

.

Какую из них удобнее
применять, зависит от конкретного вида
функций

и

.

Площадь области

:

,

называемой
криволинейным сектором, ограниченной
графиком

и двумя лучами, составляющими с полярной
осью углы

и

имеет площадь

.

Примеры:

6.1.1.
Вычислить площадь области, ограниченной
линиями:

и

.

 Изобразим фигуру
в декартовой системе координат:

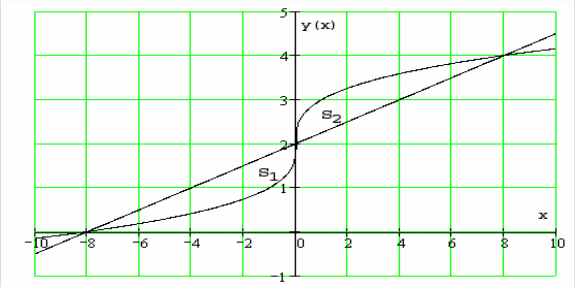
Из условия симметрии
фигуры относительно точки с координатами

,
площади

и

равны. Так как данная область является
стандартной как относительно оси

так и относительно оси

,
то ее площадь можно вычислить одним из
двух способов.

1) Выразим зависимости
в явном виде:

и
,

а стандартная
относительно оси

область

.

Тогда получаем

.

2) Заметим, что для
вычисления площади можно было
воспользоваться исходным видом
зависимостей:

.

6.1.2.
Вычислить площадь области, ограниченной
параболами

и

.

 Изобразим фигуру
в декартовой системе координат

Очевидно, область
симметрична относительно оси

,
кроме того, она не является стандартной
относительно оси

и стандартной относительно оси

,
а ее площадь можно вычислить одним из
двух способов.

1. Данная область
   не является стандартной относительно
   оси

   .
   Её можно разбить на две стандартные
   относительно оси

   области:

,

.

Из симметрии
областей

и

относительно оси

следует, что

.

1. Относительно оси

   данная область
   является стандартной:

.

Снова, используя
симметрию области, получаем

.

6.1.3.
Вычислить площадь эллипса, заданного
уравнением

(
,

).

 Искомую площадь
можно вычислить, используя как явное
представление линии, так и параметрическое.

1. Выразив уравнение
   в явном виде

,

получим,
применив подстановку

,

,
приходим к

.

2) С другой стороны,
используя параметрическое представление

,

при изменении параметра

в пределах от

до

,
получаем:

.

6.1.4.
Вычислить площадь астроиды, заданной
уравнением

(
,
)

 Изобразим кривую
в декартовых координатах:

Используя
параметрическое представление

,

при изменении параметра

в пределах от

до

,
получаем:

.

6.1.5.
Найти площадь фигуры, ограниченной
кардиоидой

,

.

 Изобразим кривую
в декартовых координатах:

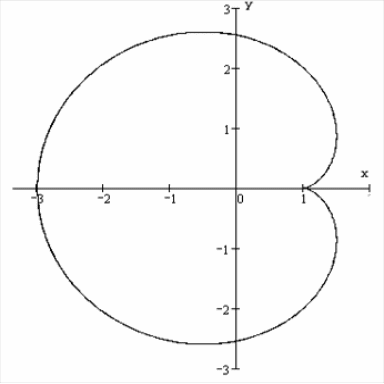
Так как кардиоида
симметрична относительно оси

,
то, используя параметрическое
представление, будем менять параметр

в пределах от

до

.
Так как

и
,

получаем по любой
из трех формул

,

,

.

Отметим, что площадь
кардиоиды задаваемой уравнением в
полярных координатах

равна

.

6.1.6.
Найти площадь области, ограниченной
кривой

.

 Кривая образует
три симметричные петли, каждая из которых
ограничивает криволинейный сектор.
Изобразим ее в полярных координатах.

Рассмотрим сектор,
лежащий в первой четверти:

.

Площадь его,
очевидно, равна 1/3 площади всей области,
ограниченной данной кривой. Следовательно,

.


Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

     Оценка интеграла. Теорема о среднем. Среднее значение функции. Продолжение. Начало здесь

     Среднее арифметическое значение функции. Значение (f(xi)), находимое по теореме о среднем, называется средним арифметическим значением функции (f(x)) в интервале ([a,b]).

     Определение. Средним арифметическим значением (y_{cp}) непрерывной функции (y=f(x)) в интервале ([a,b]) называется отношение определенного интеграла от этой функции к длине интервала: $$y_{cp}=frac{int_{a}^{b}{f(x)dx}}{b-a}.$$

Приведем некоторые соображения в обоснование этого определения.

     Пусть некоторая величина (y) принимает (n) значений (y_{1},y_{2},…,y_{n}.) Средним арифметическим значением этой величины называется частное (frac{y_{1}+y_{2}+…+y_{n}}{n},)

     Но что следует принять в качестве среднего значения непрерывной функции (y=f(x)) в некотором интервале ([a,b])?

     Разобьем интервал ([a,b]) на (n) равных частичных интервалов и возьмем значения функции в серединах этих интервалов – точках (xi _{i}): $$f(xi _{1}), f(xi _{2}), … , f(xi _{n}).$$

При таком выборе точек (xi _{i}) значения функции берутся через равные промежутки; именно так обычно поступают при всякого рода измерениях. Возьмем среднее арифметическое (eta _{n}) указанных значений: $$eta _{n}=frac{f(xi _{1})+f(xi _{2})+…+f(xi _{n})}{n}.$$

Ясно, что чем больше (n), тем больше, значений функции учитывается при отыскании среднего значения, и поэтому естественно за среднее значение (y_{cp}) функции принять предел, к которому стремится (eta _{n}) при (nrightarrowpropto). Найдем этот предел.

     Умножив и разделив выражение (eta _{n}) на (b-a), получим $$eta _{n}=frac{1}{b-a}[f(xi _{1})Delta x_{1}+f(xi _{2})+Delta x_{2}+…+f(xi _{n})Delta x_{n}],$$

где (Delta x_{1}=Delta x_{2}=…=Delta x_{n}=frac{b-a}{n}.) Преходя к переделу при (nrightarrowpropto) (при этом (Delta xrightarrow 0), поучаем указанное выше выражение для среднего значения $$y_{cp}=lim frac{1}{b-a}sum_{i=1}^{n}{f(xi _{i})Delta x_{i}}=frac{1}{b-a}int_{a}^{b}{f(x)dx}.$$

     На основании теоремы о среднем заключаем, что (y_{cp}=f(xi)), где (xi in (a,b)). Среднее значение непрерывной функции в интервале всегда (если только функция не постоянная) меньше некоторых ее значений, больше других ее значений и равно хотя бы одному ее значению

     Понятие среднего значения функции очень употребительно в технике. Многие величины часто характеризуются своими средними значениями; таковы, например, давление пара, мощность переменного тока, скорость химической реакции и т.п.

---

2012-11-06 • Просмотров [ 4385 ]

From Wikipedia, the free encyclopedia

In calculus, and especially multivariable calculus, the mean of a function is loosely defined as the average value of the function over its domain. In one variable, the mean of a function f(x) over the interval (a,b) is defined by:^[1]

Recall that a defining property of the average value of finitely many numbers
is that . In other words, is the constant value which when
added to itself times equals the result of adding the terms . By analogy, a
defining property of the average value of a function over the interval is that

In other words, is the constant value which when integrated over equals the result of
integrating over . But the integral of a constant is just

See also the first mean value theorem for integration, which guarantees
that if is continuous then there exists a point such that

The point is called the mean value of on . So we write
and rearrange the preceding equation to get the above definition.

In several variables, the mean over a relatively compact domain U in a Euclidean space is defined by

This generalizes the arithmetic mean. On the other hand, it is also possible to generalize the geometric mean to functions by defining the geometric mean of f to be

More generally, in measure theory and probability theory, either sort of mean plays an important role. In this context, Jensen’s inequality places sharp estimates on the relationship between these two different notions of the mean of a function.

There is also a harmonic average of functions and a quadratic average (or root mean square) of functions.

See also[edit]

• Mean

References[edit]