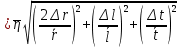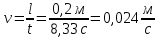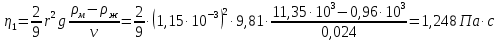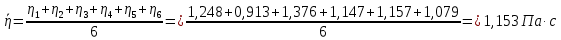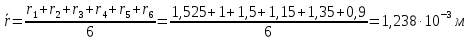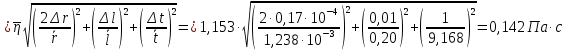Федеральное
агентство по образованию
Российской федерации
Государственное
образовательное учреждение высшего
профессионального обучения
Санкт-Петербургский
Государственный Горный Институт им.
Г.В. Плеханова
(технический
университет)
Отчёт
по лабораторной работе № 21
По дисциплине: Физика
Тема:
Определение
коэффициента вязкости жидкости
Выполнил: студент
гр. НГ-04___ _____________ Гладков
П.Д.
(подпись)
(Ф.И.О.)
П роверил:
роверил:
ассистент
____________ Чернобай
В.И.
(должность)
(подпись)
(Ф.И.О.)
Санкт-Петербург
2005
Цель работы:
определить
коэффициент вязкости жидкости методом
Стокса.
Краткое
теоретическое обоснование.
Я
внутреннего трения (вязкости) называется
появление сил трения между слоями
жидкости (или газа) движущимися друг
относительно друга параллельно и с
разными по величине скоростями.
При движении
плоских слоев сила трения между ними
согласно закону Ньютона равна:
где
– коэффициент пропорциональности,
называемый коэффициентом вязкости или
динамической вязкостью; S
– площадь соприкосновения слоев,
–
разница в скорости между соседними
слоями,
–
расстояние между соседними слоями.
Отсюда η численно
равен тангенциальной силе, приходящейся
на единицу площади соприкосновения
слоев, необходимой для поддержания
разности скоростей, равной единице,
между двумя параллельными слоями
вещества, расстояние между которыми
равно единице. В СИ единица вязкости –
паскаль·секунда.
Пусть в заполненном
жидкостью сосуде движется шарик, размеры
которого значительно меньше размеров
сосуда. На шарик действуют три силы:
сила тяжести Р, направленная вниз;
сила внутреннего трения
и выталкивающая сила Fв,
направленные вверх. Шарик сначала падает
ускоренно, но затем очень быстро наступает
равновесие, так как с увеличением
скорости растет и сила трения. Стокс же
показал, что эта сила при малых значениях
скорости пропорциональна скорости
движения шарика v и его
радиусу r:
,
где
– коэффициент вязкости.
Схема
установки.
Основные
расчетные формулы.
-
,
где
–
коэффициент вязкости, r-
радиус шарика,
–
скорость движения шарика;
-
,
где Р- сила
тяжести, действующая на шарик, FА–
сила Архимеда, Fтр–
сила внутреннего трения;
-
,
где м
– плотность материала шарика; V
– объем шарика;
-
,
где–
плотность жидкости;
-
.
Формула
расчета средней квадратичной погрешности.
,
г
–
среднее значение коэффициента вязкости,
–
значение коэффициента вязкости в каждом
отдельном опыте, n–
количество
опытов.
Таблица
измерений и вычислений.
Таблица 1
|
№ опыта |
Т |
ж |
|
d |
r |
t |
l |
v |
|
|
|
Единицы измерений |
К |
кг/м3 |
кг/м3 |
м |
м |
с |
м |
м/с |
Па·с |
Па·с |
|
1 |
298 |
0,97· 103 |
7,8· 103 |
3·10– |
1,5·10-3 |
12,11 |
0,4 |
0,033 |
1,015 |
0,07 |
|
2 |
298 |
0,97· 103 |
7,8· 103 |
3·10-3 |
1,5·10-3 |
11,88 |
0,4 |
0,034 |
0,985 |
0,07 |
|
3 |
298 |
0,97· 103 |
7,8· 103 |
3·10– |
1,5·10-3 |
12,00 |
0,4 |
0,033 |
1,015 |
0,07 |
|
4 |
298 |
0,97· 103 |
7,8· 103 |
3·10– |
1,5·10-3 |
11,91 |
0,4 |
0,034 |
0,985 |
0,07 |
|
5 |
298 |
0,97· 103 |
7,8· 103 |
3·10-3 |
1,5·10-3 |
11,88 |
0,4 |
0,034 |
0,985 |
0,07 |
|
6 |
298 |
0,97· 103 |
11,35·103 |
2,4·10-3 |
1,2·10-3 |
13,72 |
0,4 |
0,029 |
1,124 |
0,07 |
|
7 |
298 |
0,97· 103 |
11,35·103 |
2,2·10-3 |
1,1·10-3 |
16,76 |
0,4 |
0,024 |
1,140 |
0,07 |
|
8 |
298 |
0,97· 103 |
11,35·103 |
2,5·10-3 |
1,25·10-3 |
12,41 |
0,4 |
0,032 |
1,105 |
0,07 |
|
9 |
298 |
0,97· 103 |
11,35·103 |
2,1·10-3 |
1,05·10-3 |
16,93 |
0,4 |
0,024 |
1,039 |
0,07 |
|
10 |
298 |
0,97· 103 |
11,35·103 |
2,6·10-3 |
1,3·10-3 |
12,08 |
0,4 |
0,033 |
1,159 |
0,07 |
Погрешности
прямых измерений.
=0,1К;
=5·10-5м;
=
5·10-5м;
=
5·10-5м;
=0,01с.
Расчет
результатов эксперимента.
-
Рассчитываем
коэффициент вязкости жидкости для
каждого опыта:
;
Расчет для опыта
№1
η1
= (2·2,25·10-6·9,81·(7,8·103-0,97·103))/(9·0,033)
= 1,015 Па·с
η2
= 0,985 Па·с
η3
= 1,015 Па·с
η4
= 0,985 Па·с
η5
= 0,985 Па·с
η6
= 1,124 Па·с
η7
= 1,140 Па·с
η8
= 1,105 Па·с
η9
= 1,039 Па·с
η10
= 1,159 Па·с
2) η =
;
Вычисляем
среднее значение коэффициента вязкости
жидкости:
=
(η1+
η2+
η3+
η4+
η5+
η6+
η7+
η8+
η9+
η10)/10;
=(1,015+0,985+1,015+0,985+0,985+1,124+1,140+1,105+1,039+1,159)/10=1,055
Па·с.
3)
Вычисляем среднюю квадратичную
погрешность:
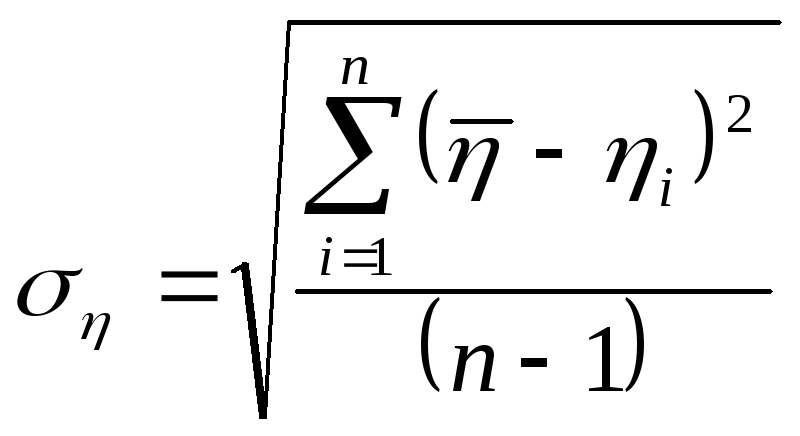
=0,07
Па·с.
Окончательный
ответ.
η =
= 1,0550,07
Па·с.
Вывод.
В данной работе
экспериментально был определен
коэффициент вязкости жидкости. Путем
постановки 10 опытов (для наибольшей
точности) со стальными и свинцовыми
шариками, удалось установить, что
скорость шарика, движущегося в сосуде
с жидкостью, зависит от размеров и
плотности шарика. В результате получили
среднее значение вязкости жидкости
(касторового масла) η=1,0550,07
Па·с. Полученный результат имеет
небольшую погрешность, что позволяет
говорить о точности расчетной формулы
и о незначительных погрешностях при
измерениях и вычислениях.
Соседние файлы в папке №21
- #
02.04.2015207.36 Кб5021.doc
- #
- #
5. измерения, указанные в пунктах 2-5,
повторяем еще для девяти шариков;
6. по расчетной формуле находим
коэффициент вязкости жидкости для каждого шарика и берем hср .
Все измеренные и
вычисленные величины записываем в таблицу.
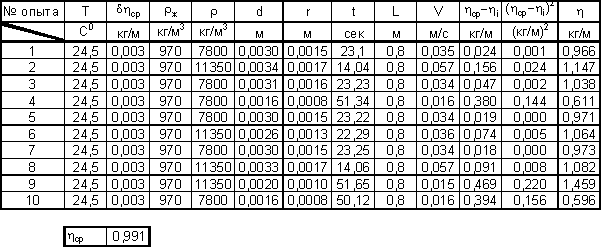
Рассчитываем среднюю квадратическую
погрешность по формуле
где
–
среднее значение коэффициента вязкости жидкости;
n – число измерений.(10 измерений)
Вывод:
Проведя данную лабораторную работу я
получил коэффициент вязкости исследуемой жидкости 0,991 кг/м, что при условии
погрешности в пределах
кг/м
не противоречит справочным данным. Исходя из этого можно сказать что
лабораторная работа была проведена успешно, с выполнением всех необходимых
условий.
Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.
Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.
Коэффициент динамической вязкости
Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.
Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:
Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.
Вязкость жидкости
Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:
-
τ – касательное напряжение;
-
µ – показатель пропорциональности, который является динамическим индексом вещества.
Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.
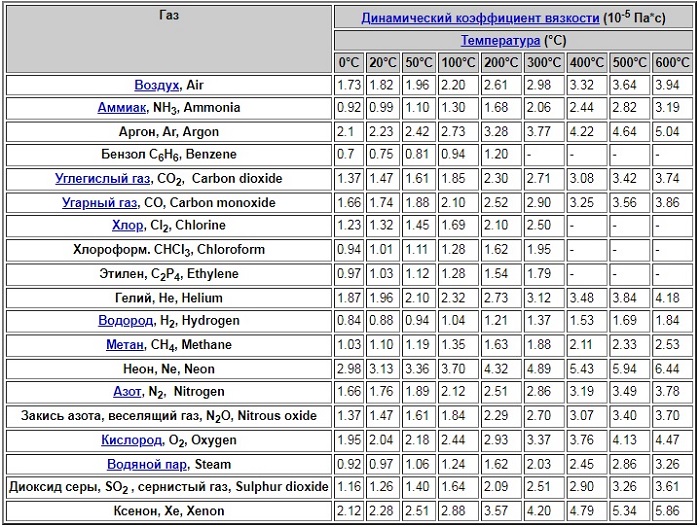
Коэффициент динамической вязкости газа
Для основных газов величины коэффициента при температуре 0 – 600 градусов Цельсия представлены в таблице:
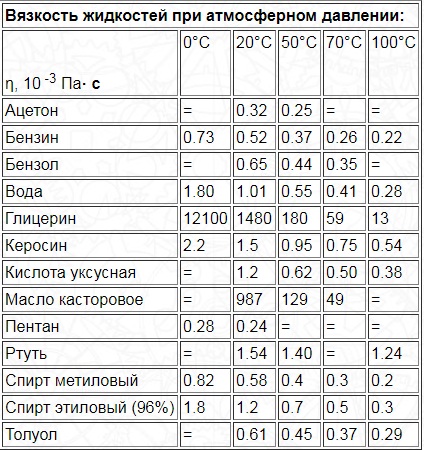
Коэффициент вязкости жидкостей
Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.
Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.
Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.
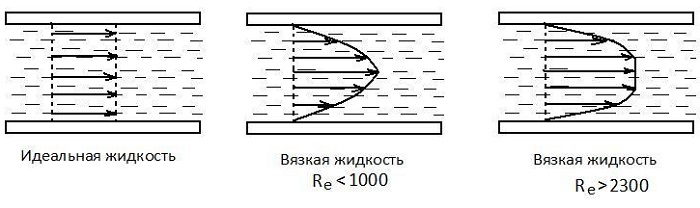
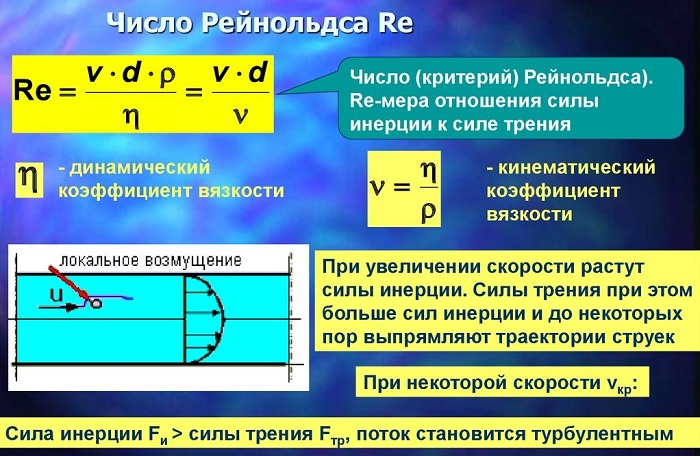
Связь коэффициента вязкости с числами Рейнольдса и силой трения
Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.
Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.
Примеры решения задач
Попробуем решить следующую задачу.
Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м3. Абсолютный индекс составляет 1•10-3 Па*с.
Действие 1.
Следует узнать эквивалентный диаметр сечения межтрубного пространства:
Действие 2.
Определение скорости воды на основе уравнения расхода:
Действие 3.
По формуле Рейнольдса найти число Re:
Подставляя значения, получаем:
Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.
Коэффициент кинематической вязкости
Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.
Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:
Действие 4. Вычисление кинематического показателя, исходя из формулы:
Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.
Заключение
Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.
Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке:
Подборка по базе: оригинал отчет 5 лаба.docx, Коржов. Отчет по учебной праткике.doc, 2022 отчет по практике.docx, 196103. Отчет.docx, Рекомендации по работе с пожилыми людьми.docx, мет рек к сам работе.docx, 3. Отчёт Асамединова.docx, Рекомендации по написанию отчета по УППП 01.docx, Лекция 7 Этические нормы и принципы в работе психолога(1).doc, Московское областное РО РКК Итоговый отчет по ПП 2022г..PDF
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей и технической физики
Отчет
по лабораторной работе №13
«Определение коэффициента вязкости жидкости»
Выполнил: студент _____________ (подпись)
Проверил: _____________
(подпись)
Дата выполнения работы:
Санкт-Петербург
2022
- Цель работы
- Определить коэффициент вязкости жидкости методом Стокса.
- Краткое теоретическое содержание
- Процесс, изучаемый в работе
- В работе производится измерение вязкости жидкости по измерению скорости установившегося равномерного движения маленьких твердых шариков при их падении в исследуемой жидкости.
- Основные определения явлений, процессов, величин
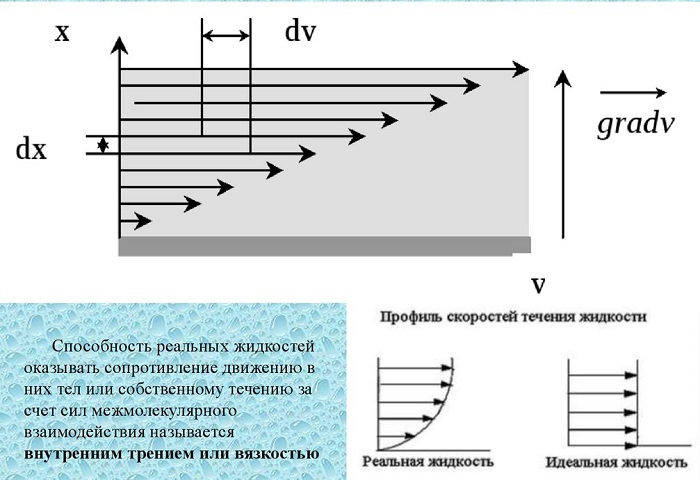
Вязкость (внутреннее трение) – есть свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одного слоя вещества относительно другого.
Градиент скорости – отношение /у, характеризующее быстроту изменения скорости, где и у – разница в скорости и расстояние между соседними слоями соответственно.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.
Скорость – это физическая векторная величина, равная отношению пути ко времени.
Ускорение – это физическая величина, численно равная изменению скорости в единицу времени.
- Основные законы и соотношения, лежащие в основе вывода расчетных формул
- При движении плоских слоев сила трения между ними согласно закону Ньютона, Н:

где 
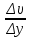
- Выталкивающая сила по закону Архимеда для шарика, Н

Где 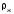


- Закон Стокса, Н

Где – коэффициент вязкости; r- радиус шарика; 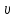
- Второй закон Ньютона, Н

Где 
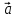
- Схема экспериментальной установки
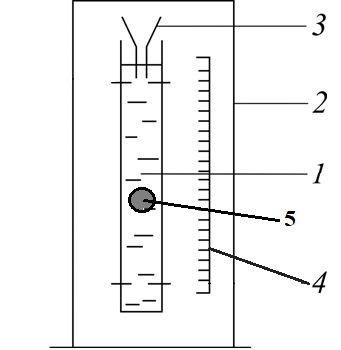
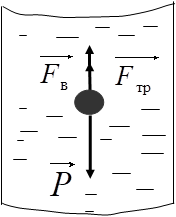
1 – Жидкость 
2 – Установка 
3 – Воронка 
4 – Линейка
5 – Шарик
- Основные расчетные формулы
- Сила внутреннего трения между слоями жидкости (закон Стокса), Н :
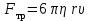
где 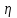
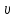
,
где Р- сила тяжести; действующая на шарик; FА– сила Архимеда; Fтр– сила внутреннего трения;
- Сила тяжести, Н
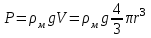
где м – плотность материала шарика; V – объем шарика;
- Выталкивающая сила, Н

где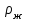


- Коэффициент вязкости жидкости,

Где 

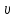

- Скорость,
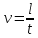
Где 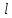
- Радиус, м

Где d – диаметр шарика.
Формулы для расчёта погрешности косвенных измерений
где 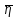
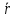

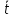
- Таблицы
«Технические данные прибора» Таблица 1
| №
п.п. |
Название прибора | Пределы измерений | Число делений | Цена деления | Класс точности | Абсолютная приборная погрешность |
| 1 | Гигрометр Психрометрический | 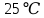 |
125 |  |
– |  |
| 2 | Микроскоп | 21,25 мм | 125 | 0,17 мм | – | 1 дел(0,17мм) |
| 3 | Цилиндрический сосуд | 1000 мм | 1000 | 1 мм | – | 1 см |
| 4 | Секундомер | 99,99 с | – | 0,01 с | – | 1 с |
«Результаты измерений» Таблица 2
| Физ. величина |
Т |
ж | | d | r | t | l | | |  |
| Ед. измер.
Номер опыта |
 |
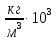 |
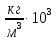 |
мм | мм | С | м | 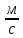 |
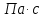 |
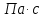 |
| 1 | 23,6 | 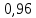 |
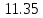 |
2,3 | 1,15 | 8,33 | 0,2 | 0,024 | 1,248 | 0,119 |
| 2 | 23,6 | 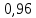 |
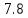 |
3,05 | 1,525 | 5,24 | 0,2 | 0,038 | 0,913 | 0,119 |
| 3 | 23,6 | 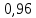 |
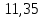 |
2,7 | 1,35 | 6,60 | 0,2 | 0,030 | 1,376 | 0,119 |
| 4 | 23,6 | 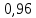 |
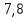 |
2 | 1 | 16,04 | 0,2 | 0,013 | 1,147 | 0,119 |
| 5 | 23,6 | 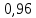 |
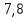 |
3 | 1,5 | 6,83 | 0,2 | 0,029 | 1,157 | 0,119 |
| 6 | 23,6 | 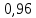 |
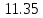 |
1,8 | 0,9 | 11,97 | 0,2 | 0,017 | 1,079 | 0,119 |
- Исходные данные:

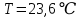
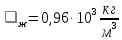

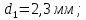
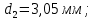




Погрешности прямых измерений:



- Вычисления
Пример вычислений для таблицы 2, опыта 1:
Радиус, м:
Скорость, 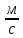
Коэффициент вязкости, 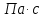
Вычисляем погрешность косвенных измерений 
Среднее значение коэффициента вязкости
Среднее значение радиуса шарика
Среднее значение времени
Погрешность косвенных измерений
- Результаты
Вывод: В данной работе экспериментально был определен коэффициент вязкости жидкости. Получили: 
Путем постановки 6 опытов со стальными и свинцовыми шариками, удалось установить, что скорость шарика, движущегося в сосуде с жидкостью, зависит от размеров и плотности шарика. Полученные результаты имеют небольшую погрешность, что позволяет говорить о точности расчетной формулы и о незначительных погрешностях при измерениях и вычислениях. Коэффициент вязкости при 
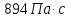
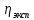

| Механика сплошных сред |
|---|
 |
| Сплошная среда |
|
Классическая механика Закон сохранения массы · Закон сохранения импульса |
|
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость |
|
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение |
|
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука |
| См. также: Портал:Физика |
Поведение жидкости с малой (сверху) и с большой (снизу) вязкостью
Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате макроскопическая работа, затрачиваемая на это перемещение, рассеивается в виде тепла. Твёрдые тела (стекло, металлы, полупроводники, диэлектрики, ферромагнетики)[1] также могут обладать вязкостью, но внутреннее трение в твёрдых телах в силу специфики явления обычно рассматривается отдельно в теории упругости и пластичности.
Механизм внутреннего трения в жидкостях и газах заключается в том, что движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Вязкость газов и жидкостей характеризуют динамическим коэффициентом вязкости (единица измерения в Международной системе единиц (СИ) — паскаль-секунда, Па·с, в системе СГС — пуаз, П; 1 Па·с = 10 П, 1 сП = 10−3 Па·с = 1 мПа·с) или кинематическим коэффициентом вязкости (единица измерения в СИ — м2/c, в СГС — стокс, Ст; 1 Ст = см2/с = 10−4 м2/с, 1 сСт = 1 мм2/с = 10−6 м2/с; внесистемная единица — градус Энглера). Кинематический коэффициент вязкости — отношение динамического коэффициента к плотности вещества. Классические методы измерения вязкости включают, например, измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром.
Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 1011—1012 Па·с.
Сила вязкого трения[править | править код]
Если параллельные плоские тела площадью S каждое, находящиеся на малом расстоянии h, движутся в той же плоскости со скоростью 

Коэффициент пропорциональности, зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости. Этот закон был предложен Исааком Ньютоном в 1687 году и носит его имя (закон вязкости Ньютона). Экспериментальное подтверждение закона было получено в начале XIX века в опытах Кулона с крутильными весами и в экспериментах Хагена и Пуазёйля с течением воды в капиллярах[2].
Эта сила называется силой вязкого трения. Её качественное отличие от сухого трения, кроме прочего, в том, что она пропорциональна скорости. Следовательно, при наличии только вязкого трения и сколь угодно малой внешней силы тело обязательно придёт в движение, то есть для вязкого трения не существует трения покоя.
Вторая вязкость[править | править код]
Вторая вязкость, или объёмная вязкость, — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и (или) при учёте неоднородности коэффициента второй вязкости по пространству.
Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.
Объёмная вязкость играет большую роль в затухании звука и ударных волн и экспериментально определяется путём измерения этого затухания.
Вязкость газов[править | править код]
В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле
где 



С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа 

Влияние температуры на вязкость газов[править | править код]
В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).
Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:[3]
где
— динамическая вязкость (в Па·с) при заданной температуре
;
— контрольная вязкость (в Па·с) при некоторой контрольной температуре
;
— заданная температура в кельвинах;
— контрольная температура в кельвинах;
— постоянная Сазерленда для того газа, вязкость которого требуется определить.
Эту формулу можно применять для температур в диапазоне 0 < 
Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже:
| Газ |  , K , K
|
 , K , K
|
 , мкПа·с , мкПа·с
|
|---|---|---|---|
| Воздух | 120 | 291,15 | 18,27 |
| Азот | 111 | 300,55 | 17,81 |
| Кислород | 127 | 292,25 | 20,18 |
| Углекислый газ | 240 | 293,15 | 14,8 |
| Угарный газ | 118 | 288,15 | 17,2 |
| Водород | 72 | 293,85 | 8,76 |
| Аммиак | 370 | 293,15 | 9,82 |
| Оксид серы(IV) | 416 | 293,65 | 12,54 |
| Гелий | 79,4[4] | 273 | 19[5] |
Вязкость жидкостей[править | править код]
Динамическая вязкость[править | править код]
Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Для так называемых ньютоновских жидкостей (которых вокруг нас большинство) справедлив общий закон внутреннего трения — закон Ньютона:
Коэффициент вязкости 

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским[6]. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества 
где:
— константа, характерная для определённой жидкости;
— собственный объём, занимаемый частицами жидкости.
Динамическая вязкость жидкостей уменьшается с увеличением температуры и растёт с увеличением давления.
Кинематическая вязкость[править | править код]
В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной
и эта величина получила название кинематической вязкости[7].
Здесь 

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом: 1 сСт = 1 мм2/c = 10−6 м2/c.
Условная вязкость[править | править код]
Условная вязкость — величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма раствора через вертикальную трубку (определённого диаметра). Измеряют в градусах Энглера (по имени немецкого химика К. О. Энглера), обозначают — °ВУ. Определяется отношением времени истечения 200 мл испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 мл дистиллированной воды из того же прибора при 20 °С. Условную вязкость до 16 °ВУ переводят в кинематическую по таблице ГОСТ, а условную вязкость, превышающую 16 °ВУ, по формуле
где 

Ньютоновские и неньютоновские жидкости[править | править код]
Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье — Стокса[8]):
где 
Среди неньютоновских жидкостей по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.
С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.[источник не указан 1003 дня]
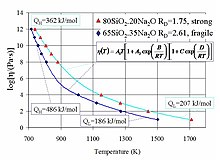
Вязкость аморфных материалов[править | править код]
Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс[9]:
где
— энергия активации вязкости (Дж/моль);
— температура (К);
— универсальная газовая постоянная (8,31 Дж/моль·К);
— некоторая постоянная.
Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости 







Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением[10]
с постоянными 




В узких температурных интервалах недалеко от температуры стеклования 
Если температура существенно ниже температуры стеклования, 
с высокой энергией активации 



При 
но с низкой энергией активации 

Относительная вязкость[править | править код]
В технических науках часто пользуются понятием относительной вязкости, под которой понимают отношение коэффициента динамической вязкости (см. выше) раствора к коэффициенту динамической вязкости чистого растворителя:
где
- μ — динамическая вязкость раствора;
- μ0 — динамическая вязкость растворителя.
Вязкость некоторых веществ[править | править код]
Для авиастроения и судостроения наиболее важно знать вязкости воздуха и воды.
Вязкость воздуха[править | править код]
Зависимость вязкости сухого воздуха от давления при температурах 300, 400 и 500 K
Вязкость воздуха зависит в основном от температуры.
При 15,0 °C вязкость воздуха составляет 1,78⋅10−5 кг/(м·с) = 17,8 мкПа·с = 1,78⋅10−5 Па·с. Можно найти вязкость воздуха как функцию температуры с помощью программ расчёта вязкостей газов[11].
Вязкость воды[править | править код]
Зависимость динамической вязкости воды от температуры в жидком состоянии (Liquid Water) и в виде пара (Vapor)
Динамическая вязкость воды составляет 8,90·10−4 Па·с при температуре около 25 °C. Как функция температуры: T = A × 10B/(T−C), где A = 2,414·10−5 Па·с, B = 247,8 K, C = 140 K.
Значения динамической вязкости жидкой воды при разных температурах вплоть до точки кипения приведены в таблице:
| Температура, °C | Вязкость, мПа·с |
|---|---|
| 10 | 1,308 |
| 20 | 1,002 |
| 30 | 0,7978 |
| 40 | 0,6531 |
| 50 | 0,5471 |
| 60 | 0,4668 |
| 70 | 0,4044 |
| 80 | 0,3550 |
| 90 | 0,3150 |
| 100 | 0,2822 |
Динамическая вязкость разных веществ[править | править код]
Ниже приведены значения коэффициента динамической вязкости некоторых ньютоновских жидкостей:
| Газ | при 0 °C (273 K), мкПа·с | при 27 °C (300 K), мкПа·с |
|---|---|---|
| воздух | 17,4 | 18,6 |
| водород | 8,4 | 9,0 |
| гелий | 20,0 | |
| аргон | 22,9 | |
| ксенон | 21,2 | 23,2 |
| углекислый газ | 15,0 | |
| метан | 11,2 | |
| этан | 9,5 |
| Жидкость | Вязкость, Па·с | Вязкость, мПа·с |
|---|---|---|
| ацетон | 3,06·10−4 | 0,306 |
| бензол | 6,04·10−4 | 0,604 |
| кровь (при 37 °C) | (3—4)·10−3 | 3—4 |
| касторовое масло | 0,985 | 985 |
| кукурузный сироп | 1,3806 | 1380,6 |
| этиловый спирт | 1.074·10−3 | 1.074 |
| этиленгликоль | 1,61·10−2 | 16,1 |
| глицерин (при 20 °C) | 1,49 | 1490 |
| мазут | 2,022 | 2022 |
| ртуть | 1,526·10−3 | 1,526 |
| метиловый спирт | 5,44·10−4 | 0,544 |
| моторное масло SAE 10 (при 20 °C) | 0,065 | 65 |
| моторное масло SAE 40 (при 20 °C) | 0,319 | 319 |
| нитробензол | 1,863·10−3 | 1,863 |
| жидкий азот (при 77K) | 1,58·10−4 | 0,158 |
| пропанол | 1,945·10−3 | 1,945 |
| оливковое масло | 0,081 | 81 |
| пек | 2,3·108 | 2,3·1011 |
| серная кислота | 2,42·10−2 | 24,2 |
| вода | 8,94·10−4 | 0,894 |
Примечания[править | править код]
- ↑ Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках: Сб. статей / Под ред. Ф. Н. Тавадзе. — М.: Наука, 1978. — 235 с.
- ↑ О некоторых ошибках в курсах гидродинамики Архивная копия от 22 декабря 2015 на Wayback Machine, с. 3—4.
- ↑ Alexander J. Smits, Jean-Paul Dussauge Turbulent shear layers in supersonic flow Архивная копия от 17 июля 2017 на Wayback Machine. — Birkhäuser, 2006. — P. 46. — ISBN 0-387-26140-0.
- ↑ Data constants for Sutherland’s formula Архивная копия от 6 марта 2018 на Wayback Machine.
- ↑ Viscosity of liquids and gases Архивная копия от 3 октября 2017 на Wayback Machine.
- ↑ Хмельницкий Р. А. Физическая и коллоидная химия: Учебних для сельскохозяйственных спец. вузов. — М.: Высшая школа, 1988. — С. 40. — 400 с. — ISBN 5-06-001257-3.
- ↑ Попов Д. Н. Динамика и регулирование гидро- и превмосистем : Учеб. для машиностроительных вузов. — М. : Машиностроение, 176. — С. 175. — 424 с.
- ↑ Седов Л. И. Механика сплошной среды Архивная копия от 28 ноября 2014 на Wayback Machine. Т. 1. — М.: Наука, 1970. — С. 166.
- ↑ Френкель Я. И. Кинетическая теория жидкостей. — Ленинград, Наука, 1975. — с. 226.
- ↑ Ojovan M. Viscous flow and the viscosity of melts and glasses. Physics and Chemistry of Glasses, 53 (4) 143—150 (2012).
- ↑ Gas Viscosity Calculator Архивная копия от 21 июля 2011 на Wayback Machine.
Литература[править | править код]
- R. H. Doremus. J. Appl. Phys., 92, 7619—7629 (2002).
- M. I. Ojovan, W. E. Lee. J. Appl. Phys., 95, 3803—3810 (2004).
- M. I. Ojovan, K. P. Travis, R. J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
- Л. И. Седов. Механика сплошной среды. Т. 1. — М.: Наука, 1970. — 492 с.
- П. Н. Гедык, М. И. Калашникова. Смазка металлургического оборудования. — М.: Металлургия, 1976. — 380 с.
- И. Ф. Голубев. Вязкость газов и газовых смесей. — М.: Физматлит, 1959.
- Ред. Ф. Н. Тавадзе Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках. — М., Наука, 1978. — 235 c.
Ссылки[править | править код]
- Аринштейн А. Сравнительный вискозиметр Жуковского // Квант, № 9, 1983.
- Измерение вязкости нефтепродуктов
- Булкин П. С. Попова И. И., Общий физический практикум. Молекулярная физика
- Градус условной вязкости // Большой энциклопедический политехнический словарь. — 2004.
- Вязкость воды



 роверил:
роверил:
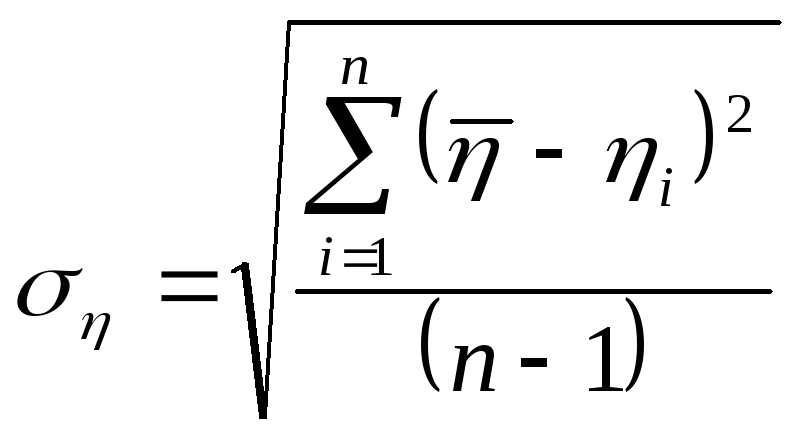
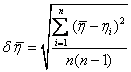
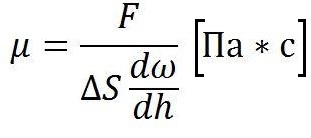
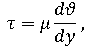

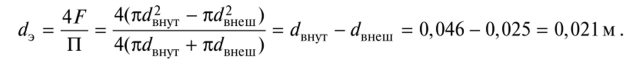
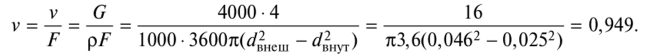
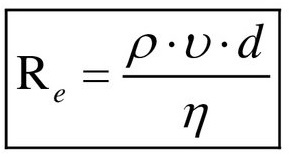
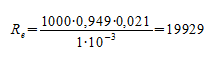
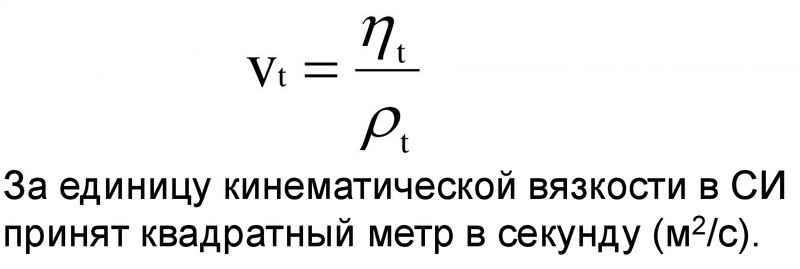
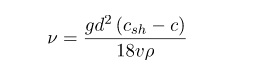


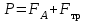 ,
,