Идеальный газ в МКТ. Среднее значение квадрата скорости молекул
- Подробности
- Обновлено 13.08.2018 12:38
- Просмотров: 734
«Физика – 10 класс»
Вспомните, что такое физическая модель.
Можно ли определить скорость одной молекулы?
Идеальный газ.
У газа при обычных давлениях расстояние между молекулами во много раз превышает их размеры. В этом случае силы взаимодействия молекул пренебрежимо малы и кинетическая энергия молекул много больше потенциальной энергии взаимодействия. Молекулы газа можно рассматривать как материальные точки или очень маленькие твёрдые шарики. Вместо реального газа, между молекулами которого действуют силы взаимодействия, мы будем рассматривать его модель — идеальный газ.
Идеальный газ — это теоретическая модель газа, в которой не учитываются размеры молекул (они считаются материальными точками) и их взаимодействие между собой (за исключением случаев непосредственного столкновения).
Естественно, при столкновении молекул идеального газа на них действует сила отталкивания. Так как молекулы газа мы можем согласно модели считать материальными точками, то размерами молекул мы пренебрегаем, считая, что объём, который они занимают, гораздо меньше объёма сосуда.
В физической модели принимают во внимание лишь те свойства реальной системы, учёт которых совершенно необходим для объяснения исследуемых закономерностей поведения этой системы.
Ни одна модель не может передать все свойства системы. Сейчас нам предстоит решить задачу: вычислить с помощью молекулярно-кинетической теории давление идеального газа на стенки сосуда. Для этой задачи модель идеального газа оказывается вполне удовлетворительной. Она приводит к результатам, которые подтверждаются опытом.
Давление газа в молекулярно-кинетической теории.
Пусть газ находится в закрытом сосуде. Манометр показывает давление газа р0. Как возникает это давление?
Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на неё с некоторой силой. В результате беспорядочных ударов о стенку давление быстро меняется со временем примерно так, как показано на рисунке 9.1. Однако действия, вызванные ударами отдельных молекул, настолько слабы, что манометром они не регистрируются. Манометр фиксирует среднюю по времени силу, действующую на каждую единицу площади поверхности его чувствительного элемента — мембраны. Несмотря на небольшие изменения давления, среднее значение давления р0 практически оказывается вполне определённой величиной, так как ударов о стенку очень много, а массы молекул очень малы.
Среднее давление имеет определённое значение как в газе, так и в жидкости. Но всегда происходят незначительные случайные отклонения от этого среднего значения. Чем меньше площадь поверхности тела, тем заметнее относительные изменения силы давления, действующей на данную площадь. Так, например, если участок поверхности тела имеет размер порядка нескольких диаметров молекулы, то действующая на неё сила давления меняется скачкообразно от нуля до некоторого значения при попадании молекулы на этот участок.
Среднее значение квадрата скорости молекул.
Для вычисления среднего давления надо знать значение средней скорости молекул (точнее, среднее значение квадрата скорости). Это не простой вопрос. Вы привыкли к тому, что скорость имеет каждая частица. Средняя же скорость молекул зависит от того, каковы скорости движения всех молекул.
Чем отличается определение средней скорости тела в механике от определения средней скорости молекул газа?
С самого начала нужно отказаться от попыток проследить за движением всех молекул, из которых состоит газ. Их слишком много, и движутся они очень сложно. Нам и не нужно знать, как движется каждая молекула. Мы должны выяснить, к какому результату приводит движение всех молекул газа.
Характер движения всей совокупности молекул газа известен из опыта. Молекулы участвуют в беспорядочном (тепловом) движении. Это означает, что скорость любой молекулы может оказаться как очень большой, так и очень малой. Направление движения молекул беспрестанно меняется при их столкновениях друг с другом.
Скорости отдельных молекул могут быть любыми, однако среднее значение модуля этих скоростей вполне определённое.
В дальнейшем нам понадобится среднее значение не самой скорости, а квадрата скорости — средняя квадратичная скорость. От этой величины зависит средняя кинетическая энергия молекул. А средняя кинетическая энергия молекул, как мы вскоре убедимся, имеет очень большое значение во всей молекулярно-кинетической теории. Обозначим модули скоростей отдельных молекул газа через υ1, υ2, υ3, … , υN. Среднее значение квадрата скорости определяется следующей формулой:
где N — число молекул в газе.
Но квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат OX, OY, OZ.
Из курса механики известно, что при движении на плоскости υ2 = υ2x + υ2y. В случае, когда тело движется в пространстве, квадрат скорости равен:
υ2 = υ2x + υ2y + υ2z. (9.2)
Средние значения величин υ2x, υ2y и υ2z можно определить с помощью формул, подобных формуле (9.1). Между средним значением 
Действительно, для каждой молекулы справедливо равенство (9.2). Сложив такие равенства для отдельных молекул и разделив обе части полученного уравнения на число молекул N, мы придём к формуле (9.3).
>Внимание! Так как направления трёх осей OX, OY и OZ вследствие беспорядочного движения молекул равноправны, средние значения квадратов проекций скорости равны друг другу:
Учитывая соотношение (9.4), подставим в формулу (9.3) 


т. е. средний квадрат проекции скорости равен 

Скорости молекул беспорядочно меняются, но средний квадрат скорости вполне определённая величина.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основные положения МКТ. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика
Почему тепловые явления изучаются в молекулярной физике —
Основные положения молекулярно-кинетической теории. Размеры молекул —
Примеры решения задач по теме «Основные положения МКТ» —
Броуновское движение —
Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел —
Идеальный газ в МКТ. Среднее значение квадрата скорости молекул —
Основное уравнение молекулярно-кинетической теории газов —
Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» —
Температура и тепловое равновесие —
Определение температуры. Энергия теплового движения молекул —
Абсолютная температура. Температура — мера средней кинетической энергии молекул —
Измерение скоростей молекул газа —
Примеры решения задач по теме «Энергия теплового движения молекул» —
Уравнение состояния идеального газа —
Примеры решения задач по теме «Уравнение состояния идеального газа» —
Газовые законы —
Примеры решения задач по теме «Газовые законы» —
Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»
Газов в природе
существует великое множество, и все они имеют определенные отличительные свойства.
Но для исследований необходимо ввести некую идеализированную модель, которая
так и называется: идеальный газ. Впервые ввести модель идеального газа
предложил Михаил Ломоносов. Большой вклад в создание такой модели, как
идеальный газ, внес Джеймс Джоуль, но все же, основной труд принадлежит
Рудольфу Клаузиусу. Именно Клаузиус ввел модель идеального газа в 1857 году.
Итак, идеальный газ — это
модель реального газа, взаимодействие между молекулами которого, пренебрежимо
мало.
Упоминая об идеальном
газе, мы предполагаем следующее:
·
Молекулы
газа очень малы и представляют собой упругие шарики.
·
Молекулы
этого газа двигаются беспорядочно.
·
Взаимодействия
между молекулами газа происходят только при соударениях, а соударения считаются
абсолютно упругими.
Конечно, такого газа в
природе не существует. Однако данная модель очень хорошо подходит для
исследования тех свойств газов, которые мы будем рассматривать в дальнейшем.
Надо сказать, что разряжённый водород, практически полностью соответствует
модели идеального газа. Впрочем, при привычных нам температурах, таких, как
комнатная температура, например, модель идеального газа достаточно хорошо
описывает реальные газы, такие, как воздух.
Рассмотрим давление газа
на стенки закрытого сосуда. Как вы знаете, давление газа возникает в результате
соударений молекул газа со стенками сосуда. Прибор, измеряющий давление,
называется манометр.
Манометр
Конечно, манометр не
может улавливать силу удара отдельных молекул. Манометр регистрирует среднюю
по времени силу, которая действует на единицу площади поверхности. Если мы
построим график зависимости давления от времени, то убедимся, что давление
постоянно меняется.
Однако наблюдаются не
хаотичные скачки давления, а сравнительно небольшие колебания вокруг какого-то
среднего значения. Поэтому, давление оказывается вполне определенной величиной.
В одном из предыдущих уроков мы убедились, что газы легко сжимаются, но при
этом повышается давление. Теперь мы можем в этом ещё раз убедиться: очевидно,
что если газ поместить в меньший объём, то количество соударений в единицу
времени увеличится. Это увеличит среднюю силу, а, значит, давление тоже
увеличится.
Но, чтобы вычислить
среднее давление, необходимо знать среднюю скорость молекул. Точнее, как мы
убедимся чуть позже, нам нужно знать значение не самой средней скорости, а
квадрата средней скорости. Конечно же, проследить за всеми молекулами газа
просто невозможно. Их очень много, все они движутся по хаотичной траектории,
преодолевая несколько сотен метров в секунду. Но нас не интересует скорость
отдельной молекулы. Нас интересует, к какому результату приводит движение всех
молекул газа.
Приведем простой пример.
Когда повар готовит ужин для большого количества людей, он не знает, кто
сколько съест.
Но повар знает какое-то
среднее количество еды, которое может съесть за ужином среднестатистический
человек, и, исходя из этого, рассчитывает количество еды, которое необходимо
приготовить.
Точно также, нам не надо
знать скорости отдельных молекул. Нам необходимо знать какое-то среднее
значение скорости, и, исходя из него, производить те или иные расчеты.
Обозначим скорости
молекул за 𝑣1,𝑣2,…,𝑣𝑛.
Тогда среднее значение квадрата скорости будет вычисляться по формуле:
Напомним, что скорость —
это векторная величина, а квадрат любого вектора равен сумме квадратов его
проекций. Значит, среднее значение квадрата скорости будет равно сумме
квадратов средних значений проекций скорости на координатные оси:
Разумеется, средние
значения квадратов проекций на оси можно определить тем же способом:
Конечно, молекулы
двигаются абсолютно беспорядочно, поэтому мы можем считать проекции на все три
оси равноправными. То есть, мы справедливо можем предположить, что проекция на
ось х равна проекциям на оси у и z.
Таким образом, мы можем заключить, что среднее значение квадрата проекции
скорости на любую ось равно одной третьей среднего значения квадрата самой
скорости:
Напомним, что каждое
тело, в частности газ, обладает макроскопическими и микроскопическими
параметрами. К макроскопическим параметрам относятся давление, температура и
объём. Как правило, именно с помощью макроскопических параметров мы
характеризуем то или иное тело. Но макроскопические параметры зависят от
микроскопических, таких, как масса, размеры и скорости молекул. В ближайшее
время мы будем заниматься изучением того, как макроскопические параметры газа
зависят от микроскопических.
Среднее значение квадрата скорости
Нас будет интересовать
средний квадрат проекции скорости. Он
находится так же, как квадрат модуля
скорости (см. выражение (4.1.2)):
(4.3.2)
Скорости
молекул принимают непрерывный ряд
значений. Определить точные значения
скоростей и вычислить среднее значение
(статистическое среднее) с помощью
формулы (4.3.2) практически невозможно.
Определим
несколько иначе, более реалистично.
Обозначим черезп1
число
молекул в объеме 1 см3,
имеющих проекции скоростей, близкие к
v1х;
через
п2
—
число молекул в том же объеме, но со
скоростями, близкими к vkx,
и
т. д.* Число молекул со скоростями,
близкими к максимальной vkx,
обозначим
через nk
(скорость
vkx
может
быть сколь угодно велика). При этом
должно выполняться условие: п1
+ п2
+ …
+ ni
+
… + nk
= п, где
п
— концентрация
молекул. Тогда для среднего значения
квадрата проекции скорости вместо
формулы (4.3.2) можно написать следующую
эквивалентную формулу:
* О том, как эти
числа могут быть определены, будет
рассказано в §4.6.
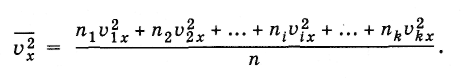
(4.3.3)
Так
как направление X
ничем
не отличается от направлений Y
и Z
(опять-таки
из-за хаоса в движении молекул), справедливы
равенства:
(4.3.4)
Для каждой молекулы
квадрат скорости равен:
Значение среднего
квадрата скорости, определяемое так
же, как средний квадрат проекции скорости
(см. формулы (4.3.2) и (4.3.3)), равно сумме
средних квадратов ее проекций:
(4.3.5)
Из выражений
(4.3.4) и (4.3.5) следует, что
(4.3.6)
т.
е. средний квадрат проекции скорости
равен
среднего квадрата самой скорости.
Множительпоявляется вследствие трехмерности
пространства и, значит, существования
трех проекций у любого вектора.
Скорости
молекул беспорядочно меняются, но
среднее значение проекций скорости на
любое направление и средний квадрат
скорости —
вполне
определенные величины.
§ 4.4. Основное уравнение молекулярно-кинетической теории
Вычислим с помощью
молекулярно-кинетической теории давление
газа. На основе проделанных расчетов
можно будет сделать очень важный вывод
о связи температуры газа со средней
кинетической энергией молекул.
Пусть газ находится
в прямоугольном сосуде с твердыми
стенками. Газ и сосуд имеют одинаковые
температуры, т. е. находятся в состоянии
теплового равновесия. Будем считать
столкновения молекул со стенками
абсолютно упругими. При этом условии
кинетическая энергия молекул в результате
столкновения не меняется.
Требование того,
чтобы столкновения были абсолютно
упругими, не является строго обязательным.
В точности оно и не реализуется. Молекулы
могут отражаться от стенки под разными
углами и со скоростями, не равными по
модулю скоростям до соударения. Но в
среднем кинетическая энергия отраженных
стенкой молекул будет равна кинетической
энергии падающих молекул, если только
существует тепловое равновесие.
Результаты расчета не зависят от
детальной картины столкновений молекул
со стенкой. Поэтому вполне допустимо
считать столкновения молекул подобными
столкновениям упругих шаров с абсолютно
гладкой твердой стенкой.
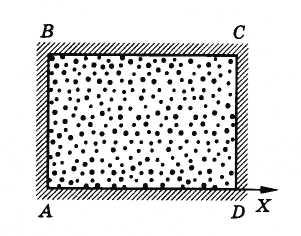
Вычислим
давление газа на стенку сосуда CD,
имеющую
площадь S
и расположенную перпендикулярно оси X
(рис.
4.3).
Рис. 4.3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Средняя скорость молекул
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
υotn=28kTπm0=2υ.
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
υkυ=1N∑i=1Nυi2
Формулу средней квадратичной скорости можно переписать так:
υkυ2=∫0∞υ2Fυdυ.
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
υkυ=3kTm0=3RTμ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
p=13nm0υkυ,
где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
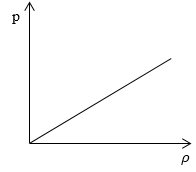
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).
Рисунок 1
Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
υ=8kTπm0
Из графика видно, что p~ρ или p=Cρ, где C – это некоторая константа.
m0=ρn, p=nkT=Cρ→kT=Cρn
Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:
υ=8kTπm0=8Cρπnnρ=8Cπ
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?
Решение
Применим выражение для υkυ:
υkυ=3RTμ
Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:
pV=mμRT=NNART.
Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:
p=nNART→RT=pNAn
Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:
υkυ=3pNAμn
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.
Средняя квадратичная скорость — среднее квадратическое значение скоростей всех молекул данного количества газа. Измеряется в (м^2/с^2.)
Что оказывает влияние на скорость молекул
На быстроту движения молекул в газе оказывают влияние следующие параметры:
- Давление (возникает в результате ударов частиц о стенки сосуда).
- Концентрация частиц (количество частиц в единице объема).
- Температура (с увеличением температуры, частицы начинают двигаться быстрее, с уменьшением — замедляются).
- Масса молекул.
Эта взаимозависимость выражается главным уравнением молекулярно-кинетической теории идеального газа:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(P=frac13times m_0times ntimes V^2)
Где P — давление газа в Паскалях, (m_0) — масса молекулы в килограммах, n — концентрация частиц в (м^3), V — скорость движения молекул в м/с.
Расчет по формуле
Для определения средней квадратичной скорости (обозначение — v) всех молекул в газе, нужно вычислить квадратный корень из средней арифметической величины квадратов скоростей каждой частицы.
В виде формулы это выглядит так:
(v=sqrt{frac{v_1^2+v_2^2+…v_n^2}N})
Где (v_1) — (v_n) — это скорости молекул, N — их число в газе.
Расчет значения по такой формуле очень громоздок и сложен, поэтому для определения значения средней квадратичной скорости используют следующее уравнение:
(v=sqrt{frac{3times Rtimes T}M})
Где R — универсальная газовая постоянная, равная примерно 8,31 Дж/Кхмоль, T — температура в Кельвинах, M — молярная масса в кг/моль.
Получается такое уравнение путем преобразования основного уравнения кинетической теории газов.