Подборка по базе: ТИТУЛ_ПП_содержание отчета_образец заполнения.docx, астанин практика отчет.docx, Методические указания по рейтинговой работе дисциплина Государс, Титул отчета 2022-2023.docx, бух учет и фин отчетность СКИНУТЬ!.docx, годовой отчет воспитателя (сред гр.docx, 193428. Отчет.docx, положение о работе с одаренными детьми.docx, 3. Отчет..docx, Титульный лист отчета о прохождении практики (2).docx
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧСЕКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ 
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей и технической физики
Отчет по лабораторной работе №10
По дисциплине Физика (наименование учебной дисциплины согласно учебному плану)Тема: Определение модуля упругости (модуль Юнга) по деформации изгиба
Выполнил: студент гр.
МЦ-21-2 Пашнина Ю.Е
(группа) (подпись) (Ф.И.О.)
ОЦЕНКА:
Дата:
Проверил: (должность) (подпись) (Ф.И.О.)
Санкт-Петербург 2022 год
Лабораторная работа №10
«Определение модуля упругости (модуль Юнга) по деформации изгиба»
Цель работы: определить модуль Юнга материала путём измерения прогиба стержня при максимальной нагрузке.
Явление, изучаемое в работе: деформация изгиба.
Краткое теоретическое содержание.
Деформация называется упругой, если она исчезает после прекращения действия силы. При упругой деформации, по закону, экспериментально установленному Гуком, величина абсолютной деформации Δlпропорциональна приложенной силе F:
| 𝐹 = 𝑘∆𝑙 | (1) |
Где k– постоянная величина для данного образца.
Модуль Юнга – физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации.
Физический смыл модуля юнга – модуль Юнга численно равен нормальному напряжению, при котором длина деформируемого стержня изменилась бы в два раза.
Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчётные формулы.

| ∆𝑙 1 𝐹 𝜎
𝑙 = 𝐸 𝑆 или 𝜀 = 𝐸 |
(2) |

𝑙

𝑆
S– площадь поперечного сечения, [S] = м2;
F– приложенная сила, [F] = Н;
l– первоначальная длина тела, [l] = м;
Δl – абсолютное удлинение стержня, [Δl] = м;
E–коэффициент пропорциональности (модуль Юнга), [E] = Н/м2.

Основные расчётные формулы.

где F−приложенная в центре стержня сила, [F] = Н;
ω, h – размеры поперечного сечения стержня, [ω] = м, [h] = м;
Y– стрела прогиба стержня под нагрузкой, [Y] = м;
L– расстояние между опорами балки, [L] = м;
E–модуль Юнга, [E] = Н/м2.
Формула для расчёта погрешности косвенных измерений.

где Е – среднее значение модуля Юнга, [E] = H/м2
ω, h – размеры поперечного сечения стержня, [ω] = м, [h] = м;
L– расстояние между опорами балки, [l] = м;
E–модуль Юнга, [E] = Н/м2;
Δω,Δh– погрешность прямых измерений размеров поперечного сечения стержня, [Δω] = м, [Δh] = м;
Δl – погрешность прямых измерений расстояния между опорами балки, [Δl] = м;
– среднее значение, [F] = Н/м; [] = H/м;
𝛥
– погрешность измерений величины, [𝛥] = H/м;
Относительная погрешность измерений модуля Юнга.

Где 
Ē – среднее значение модуля Юнга, [ Ē ] = Н/м2.
Погрешность прямых измерений.
Погрешность измерения массы грузов, Δm = 0,1 кг;
Погрешность измерения стрелы прогиба, ΔY= 0,01 мм;
Погрешность измерения размеров поперечного сечения стержня, Δω=Δh=0,05 мм
Погрешность измерения расстояния между опорами балки, ΔL= 1 мм.
Таблица 1
Измерение размеров поперечного сечения бруска
| № | h | hср | 𝛥h | w | wср | 𝛥w |
| Ед. изм. Номер опыта |
мм | мм | мм | мм | мм | мм |
| 1 | 3 |
3 |
0,05 |
10,5 |
10,47 |
0,05 |
| 2 | 2,9 | 10,4 | ||||
| 3 | 3,1 | 10,5 |
Таблица 2
Результаты измерений и вычислений
| № | масса груза | F | n | Y | F/Y | E | |
| Ед. изм. Номер опыта |
кг |
Н |
делений |
м |
Н/м |
Н/м |
Н/м2 |
| 1 | 0,1 | 0,981 | 20 | 0,2*10-3 | 4905,00 |
4019,24 |
144,41*109 |
| 2 | 0,2 | 1,962 | 46 | 0,46*10-3 | 4265,22 | 125,57*109 | |
| 3 | 0,4 | 3,924 | 100 | 1*10-3 | 3924,00 | 115,53*109 | |
| 4 | 0,65 | 6,377 | 164 | 1,64*10-3 | 3888,11 | 114,47*109 | |
| 5 | 0,95 | 9,319 | 243 | 2,43*10-3 | 3835,19 | 112,91*109 | |
| 6 | 1 | 9,810 | 255 | 2,55*10-3 | 3847,06 | 113,26*109 | |
| 7 | 0,95 | 9,319 | 244 | 2,44*10-3 | 3819,47 | 112,45*109 | |
| 8 | 0,65 | 6,377 | 170 | 1,7*10-3 | 3750,88 | 110,43*109 | |
| 9 | 0,4 | 3,924 | 101 | 1,01*10-3 | 3885,15 | 114,38*109 | |
| 10 | 0,2 | 1,962 | 49 | 0,49*10-3 | 4004,08 | 117,88*109 | |
| 11 | 0,1 | 0,981 | 24 | 0,24*10-3 | 4087,50 | 120,34*109 |
Расчёты.
Исходные данные:
- Металлический стержень (балка);
- Расстояние между опорами балки L = 322 мм;
- Погрешность прямых измерений 𝛥m = 0,1 г; 𝛥Y = 0,01 мм; 𝛥w = 𝛥h = 0,05 мм; 𝛥L = 1мм
Вычисления:
Таблица 1. Расчёт средних значений поперечного сечения стержня.
n = 3
Таблица 2. Пример вычисления для опыта №1.
- Сила, которая действует на балку.

- Стрела прогиба балки.

- Значение F/Y.

- Модуль Юнга для стержня.

- Среднее значение F/Y.
n = 11
- Среднее значение модуля Юнга для стержня.

- Квадратичная погрешность измерений модуля Юнга.

- Относительная погрешность.

График 1.
Зависимость стрелы прогиба от силы тяжести при увеличении нагрузки стержня.
Y=Y(F)
График 2.
Зависимость стрелы прогиба от силы тяжести при уменьшении нагрузки стержня.
Y=Y(F)
Результат
Модуль Юнга с учетом абсолютной погрешности косвенных измерений.
E = Ē
Сравнительная оценка результата
Полученное значение модуля Юнга наиболее приближено к модулю Юнга цинка (Ец = 120
Сравнительная оценка.
Вывод.
В ходе лабораторной работы удалось установить модуль Юнга для металлического стержня методом прогиба балки под нагрузкой. Наиболее приближенным теоретическим значением к экспериментальному значению оказался модуль Юнга цинка. Расхождение экспериментального результата с теоретическим составило 1,11%.
Данная погрешность косвенных измерений объясняется тем, что мы пользовались механическим стрелочным манометром. В данном приборе присутствует трение механизмов, которое иногда не позволяет точно определить стрелу прогиба. Также мы не можем утверждать, что работали со стержнем, у которого нет внутренних дефектов, которые могут влиять на значение модуля Юнга материала.
Лабораторная
работа №2
Определение
модуля Юнга методом растяжения струны
группа
Р-02
Выполнил:
Еремеев Е.Е.
Проверил:
Савельев Н.П.
Цель
Работы:
Определение модуля Юнга, обучение работы
с катетометром, микрометром, научиться
обрабатывать эксперементальные данные.
Измерение
диаметра струны
|
W |
1 |
2 |
3 |
4 |
5 |
<d> |
|
D, |
0,35 |
0,35 |
0,34 |
0,35 |
0,35 |
0,35 |
Измерение
абсолютного удлинения струны
|
№ измерения |
X0, |
Х1,мм |
Х0-Х1,мм |
X2, |
X0-X2, |
X3, |
X0-X3 |
|
1 |
45.625 |
45.268 |
0.357 |
45.019 |
0.606 |
44.539 |
1.086 |
|
2 |
45.835 |
45.246 |
0.589 |
45.018 |
0.817 |
44.535 |
1,300 |
|
3 |
45.771 |
45.300 |
0.471 |
45.019 |
0.752 |
44.434 |
1.337 |
|
4 |
45.705 |
45,373 |
0.332 |
44.935 |
0.470 |
44.594 |
0.811 |
|
5 |
45.836 |
45.509 |
0.327 |
44.995 |
0.847 |
44.243 |
1.593 |
|
<X-Xi> |
——— |
——— |
0.415 |
——— |
0.697 |
——— |
1.225 |
<
x
>=(1/n)∙
– вычисление
среднего арифметического.
<
Х0-Х1
>=0.415
<
Х0-Х2
>=0.697
<
Х0-Х3
>=1.225
<d>=0.35
Sn=
– вычисление
средней квадратичной погрешности.
(1)Sn=0.112
(2)Sn=0.156
(3)Sn=0.277
(d)Sn=0.05
S=
– вычисление
средней квадратичной погрешности
среднего арифметического.
(1)S=0.050
(2)S=0.069
(3)S=0.124
(d)
S=0.022
∆(x)cл=tα,n∙S
– вычисление
случайной погрешности;
α=0,95;
n=5,
значит
из таблицы коэффициентов Стьюдента
следует, что tα,n=2,8
∆ (Х0-Х1)
сл=0.14
∆(Х0-Х2)
сл=0.19
∆(Х0-Х3)
сл=0.34
∆(d)
сл=0.022
∆(x)=
– абсолютная
погрешность;
∆xсист
– систематическая погрешность.
∆(Х0-Х1)
=0.14
∆(Х0-Х2)
=0.19
∆(Х0-Х2)
=0.34
∆(d)
=0.02
δ=∆(x)
/<
x
> – относительная
погрешность.
δ1=0.33
δ2=0.27
δ3=0.25
δd=0.06
∆l=kF
S=
F=mg
(Х0-Хi)
=(4l0mg)/
(
E)
E=(4l0mg)/
((Х0-Хi)
E1=9.016
E2=
E3=9.200
<E>=
(E1+E2+E3)/3
<E>=9.4
δ=
– относительная
погрешность.
δE=
δE1=0.356
δE2=0.295
δE3=0.300
∆E=1/3
среднего значения модуля Юнга.
∆E=0.184
E=9.4
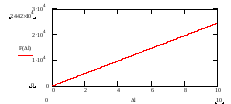
График
зависимости абсолютного удлинения
струны от приложенной силы.
По
построенному графику F(
можно найти модуль Юнга.
Для
этого вычислим tg
угла наклона графика к оси F.

Вывод:
Согласно
полученным данным и визуальным наблюдениям
пришли к выводу, что струна сделана из
меди.
Ответы
на контрольные вопросы:
-
Сила
упругости прямо пропорциональна
деформации пружины. -
Число
измерений следует выбирать из соображения
проведения максимального количества
измерений за время выделенное на их
снятие, т.к. при большем количестве
измерений можно добиться более маленькой
погрешности (большей точности), чем при
меньшем количестве этих измерений.
Число измерений должно быть больше
одного. -
Инструмент
измерения выбирается из соображения
удобности измерения этим прибором и
требуемой точности измерения. -
Величину
нагрузки не следует учитывать, т.к.
модуль Юнга не зависит от массы груза,
а зависит от рода веществ и его упругих
свойств. -
Длинна
струны
l0
дана
с
точностью =
0.5
см;
масса груза m
дана
с точностью =
60
мг. -
Для
вычисления погрешности косвенных
измерений воспользуемся формулой: δ=
E=
Находим
частную производную:
δE=
-
Систематическая
погрешность микрометра =
0.001
мм; систематическая погрешность
катетометра =0.03
мм.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Модуль Юнга
Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела.
Это свойство любого материала, и оно зависит от температуры и оказываемого давления.
В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации.
Другими словами: когда тело деформируется, то появляется сила, которая стремится восстановить первоначальную форму и размер тела. Сила упругости является этой проявляющейся силой. Также она представляет собой следствие электромагнитного взаимодействия между частицами.
Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным.
Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.
Примеры значений модуля Юнга (упругости) для:
(т.е. для резины он в 5 раз меньше стали)
Таблица
Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи “гигапаскалей” ([ГПа]; ).
| Материал | Модуль Юнга E, [ГПа] |
|---|---|
| Алмаз | 1220 |
| Алюминий | 69 |
| Дерево | 10 |
| Кадмий | 50 |
| Латунь | 97 |
| Медь | 110 |
| Никель | 207 |
| Резина | 0,9 (≈ 1 МПа, мегапаскаль) |
| Сталь | 200 |
| Титан | 107 |
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):
Где:
- σ — механическое напряжение
- E — модуль Юнга (модуль упругости)
- ε — относительное удлинение
Закон Гука (этот описывает явления в теле)
Где:
- Fупр — сила упругости
- k × Δl — удлинение тела
Где:
- Fупр — сила упругости
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина тела
- Δl — удлинение тела
Где:
- Fупр/S — механическое напряжение, обозначается как σ
- Δl/l — относительное удлинение, обозначается как ε
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.
Другие формулы вычисления модуля Юнга (модуля упругости)
Где:
- E — модуль Юнга (модуль упругости)
- k — жёсткость тела
- l — первоначальная длина стержня
- S — площадь поперечного сечения
Либо можно выразить k (жёсткость тела):
Где:
- k — жёсткость тела
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина стержня/тела
Пример решения задачи (через закон Гука):
Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.
Дано:
Будем искать через закон Гука (σ = E × ε).
Помним из закона Гука:
σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)
ε = Δl/l (а это относительное удлинение, обозначается как ε)
Подставляем в формулу (σ = E × ε):
Например, в нашей таблице такой модуль Юнга имеет кадмий.
Узнайте также про:
- Напряжённость электрического поля
- Законы Ньютона
- Закон сохранения энергии
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Закон Гука формула. Модуль Юнга
Для большинства конструкционных материалов между напряжением (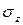
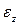
Закон Гука: Напряжение пропорционально деформации.
Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила».
К такому же заключению в 1680 г., независимо от Гука, пришел французский ученый Эдмон Мариотт.
Коэффициент пропорциональности (E) в формуле закона Гука 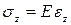
Необходимо отметить, что некоторые материалы не подчиняются закону Гука, например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения.
Из закона Гука видно: чем больше модуль Юнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модуль Юнга измеряется в тех же единицах, что и нормальное напряжение (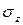
Так, например, для всех марок сталей 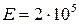








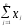




















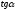
 0.5
0.5 60
60

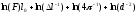



 0.001
0.001 0.03
0.03
