Теорема о среднем.
Если f(x) непрерывна на отрезке [a,b], то
существует точка
,
такая что
Док-во. Функция, непрерывная на отрезке,
принимает на этом отрезке своё наименьшее
m и наибольшее M значения. Тогда
Число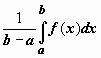
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между m и M. Таким образом, существует
точка,
такая что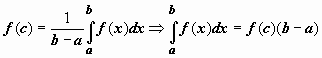
Это свойство имеет простую геометрическую
интерпретацию: еслинепрерывна
на отрезке [a,b], то существует точкатакая,
что площадь криволинейной трапеции
ABCD равна площади прямоугольника с
основанием [a,b] и высотой f(c) (на рисунке
выделен цветом).
7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
Рассмотрим функцию
f (x), интегрируемую по Риману на отрезке
[a, b]. Раз она интегрируема на [a, b], то она
также интегрируема на [a, x] ∀x
∈
[a, b]. Тогда при каждом x ∈
[a, b] имеет смысл выражение
,
и при каждом x оно равно некоторому
числу.
Таким образом,
каждому x ∈
[a, b] поставлено в соответствие некоторое
число
,
т.е. на [a, b] задана
функция:
(3.1)
Определение:
Функция F (x), заданная
в (3.1), а также само выражение
называется
интегралом с
переменным верхним пределом. Она
определена на всем отрезке [a, b]
интегрируемости
функции f (x).
Теорема:
Условие: f (t)
непрерывна на [a, b], а функция F (x) задана
формулой (3.1).
Утверждение: Функция
F(x) дифференцируема на [a, b], причем F (x)
= f (x).
(В точке a она
дифференцируема справа, а в точке b –
слева.)
Доказательство:
Поскольку для
функции одной переменной F (x)
дифференцируемость равносильна
существованию производной во всех
точках (в точке a справа, а в точке b –
слева), то мы найдем производную F (x).
Рассмотрим разность
Таким образом,
,
при этом точка ξ
лежит на отрезке [x, x + ∆x] (или [x + ∆x, x]
если ∆x < 0).
Теперь вспомним,
что производная функции F(x) в заданной
точке x ∈
[a, b] равна пределу разностного отношения:
.
Из равенства имеем:
,
Устремляя теперь
∆x →
0, в левой части данного равенства получим
F’(x), a в правой
Вспомним определение
непрерывности функции f (t) в точке x:
Пусть x1 в этом
определении равен ξ. Поскольку ξ ∈
[x + ∆x, x] (ξ ∈
[x, x + ∆x]), а
∆x →
0, то |x − ξ| →
0, и по определению непрерывности, f (ξ)
→
f (x). Отсюда имеем:
F’(x) = f (x).
Следствие:
Условие: f (x)
непрерывна на [a, b].
Утверждение: Любая
первообразная функции f (x) имеет вид
где C
∈
R – некоторая константа.
Доказательство.
По теореме 3.1 функция
является
первообразной для
f(x). Предположим,
что G(x) – другая первообразная f (x).
Тогда G’(x) = f(x) и для функции F(x) − G(x)
имеем: (F
(x) + G(x))’ = F’(x)−G’(x) = f (x)−f(x) ≡
0. Значит, производная функции F (x)−G(x)
равна нулю,
следовательно, эта функция есть
постоянная: F(x) − G(x) = const.
8. Формула Ньютона-Лейбница для определенного интеграла.
Теорема:
Условие:
f(t) непрерывна на [a, b], а F(x) ее любая
первообразная.
Утверждение:
Доказательство:
Рассмотрим некоторую первообразную F
(x) функции f (x). По Следствию из Теоремы
«О дифференцируемости интеграла с
переменным верхним пределом» (см.
предыдущий вопрос) она имеет вид
.
Отсюда
=>
c=F(a),
и
.
Перенесем F(a) в
последнем равенстве в левую часть,
переобозначим переменную интегрирования
снова через x и получим формулу Ньютона
– Лейбница:
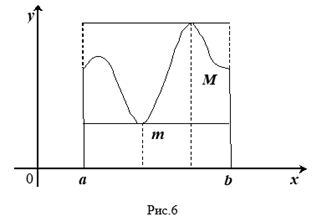
I. ОцеНКа интеграла. Укажем граНИцы, между которыми наверняка заключено значение интеграла.
Теорема VI (об оценке определенного интеграла). Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т. Е.
Где Т и М — Соответственно наименьшее и наибольшее значения функции интервале
:
Доказательство. Возьмем две функции и
. Первая из них в интервале
неотрицательна, вторая неположительна. Значит, по теореме V
и
А по теореме I
и
Откуда в силу того, что
И
Что и требовалось доказать.
Геометрический смысл этих неравенств таков: площадь КриволиНейной трапеции больше площади прямоугольника с основанием, РавНой оснОваНИЮ трапеции, и высотой, равной наименьшей ординате ТрапециИ, и меньше площади прямоугольника с тем же основанием и Высотой, равной наибольшей ординате Трапеции (рис. 6).
Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или дажЕ невозможно найти точное значение Интеграла, а оценивая его, мы узнаем, ХотЯ бы грубо, приближенное его Значение. С такого, рода оценками приходится Довольно часто встречаться в математике.
УказаННые в теореме VI границы для Интеграла тем более точны, чем короче Интервал интегрирования и чем меньше линия отличается По положению от прямой, параллельной оси Ох.
Пример. Оценим интеграл
Легко проверить, что подынтегральная функция в интервале убывает и, следовательно,
Т. е.
Таким образом, интеграл заключен между 0,5 и 0,71, что дает нам право считать его равным 0,6 с точностью до 0,1. Более точные приемы показывают, что приближенно он равен 0,62.
II. Обобщение теоремы об оценке интеграла. Интегрирование неравенств.
Справедлива следующая более общая теорема, чем теорема VI:
Теорема VII. Если в каждой точке Х интервала
То
Это значит, что неравенство между функциями влечет неравенство того же смысла между их определенными интегралами, или, говоря коротко, Неравенства можно интегрировать..
На доказательстве и геометрическом смысле теоремы останавливаться не будем, так как они вполне подобны предыдущим.
В частном случае, когда тождественно равно М, а
тождественно равно Т, получаем теорему VI.
III. Теорема о среднем.
Определенный интеграл обладает следующим важным свойством:
Теорема VIII (о среднем). Внутри интервала интегрирования существует, по меньшей мере, одно значение
для которого
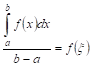
Доказательство. В силу теоремы VI имеем:
И, значит,
Где M — некоторое число, заключенное между наименьшим (Т) и наибольшим (М) значениями функции в интервале
, Т. Е.
. Но
, будучи непрерывной функцией, обязательно принимает, по меньшей мере, один раз каждое значение, лежащее между Т и М. Следовательно, при некотором
получит значение, равное M, т. е.
(см. рис. 6), что и требовалось доказать.
Из равенства (*) находим:
Эта формула позволяет теорему о среднем высказать в такой форме:
ОпредЕЛенный интеграл от непрерывной функции, равен произведению значения этой функции в некоторой промежуточной точке интервала интегрирования, на длину интервала.
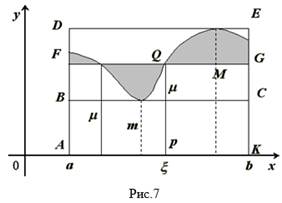
Дадим наглядное пояснение теоремы. При движении прямой, параллельной оси Ох (рис. 6), вверх от положения ВС площадь прямоугольника АВСК будет непрерывно возрастать от величины, меньшей площади трапеции, до величины, большей ее. Очевидно, при некотором промежуточном положении прямой — обозначим его через FG — Площадь прямоугольника AFGK окажется в точности равной площади трапеции S. Так как при ЭТом движении прямая постоянно пересекает линию, ограничивающую трапецию, то и в положении FG найдется одна или несколько (на рис.
7 две)
Точек пересечения Q; абсцисса любой точки пересечения и будет требуемым по теореме значением X.
Если трапецию ограничивает прямая линия, то ; отрезок PQ будет при этом средней линией прямолинейной трапеции.
IV. Среднее арифметическое значение функции. Значение , находимое по теореме о среднем, называется средним арифметическим значением функции
в интервале
.
Определение. Средним арифметическИМ значением непрерывной функции
в интервале
называется отношение определенного интеграла от этой функции к длиНЕ интервала:
Приведем некоторые соображения в обоснование этого определения.
Пусть некоторая величина У принимает П значений: Средним арифметическим значением этой величины называется частное
. ТаК если температура воздуха в течение суток измеряется через каждый час, то средней температурой будет частное от деления суммы всех наблюденных температур на 24.
Но представим себе теперь, что величина изменяется непрерывно (например, температура воздуха известна в любой момент суток) и мы хотим как-то в среднем охарактеризовать всю совокупность ее значений. Как в этом случае следует определить среднюю температуру воздуха, принимая во внимание всю известную совокупность знАЧений температуры? Вообще, ЧтО следует принять в качестве среднего значения неПРерывной фуНКции в некотором интервале
?
Разобьем интервал на П равных частей с помощью точек
и возьмем значения функции в этих N точках:
Значениями нашей функции во всех остальных точках интервала пока пренебрежем. Возьмем среднее арифметическое указанных значений:
Ясно, что чем больше П, тем больше значений функции учитывается при отыскании среднего значения, и поэтому естественно за среднее значение функции принять предел, к которому стремится
При
. Найдем этот предел.
Умножив и разделив выражение для на
, получим:
Но так как То
ОТкуда, переходя к пределу, получаем указанное нами выше выражение для среднего значения:
На основании теоремы о среднем (теорема VIII) мы заключаем, ЧТо , где
, т. Е. что среднее значение непрерывной функции в интервале всегда (если только функция не постоянная) меньше некоторых ее значений, больше других ее значений и равно по меньшей мере одному ее значению.
Понятие среднего значения функции очень употребительно в техНИке. Многие величины часто характеризуются своими средними значениями; таковы, например, давление пара, сила и напряжение переменного тока, скорость химической реакции и т. п.
| < Предыдущая | Следующая > |
|---|
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 мая 2018 года; проверки требует 1 правка.
Первая теорема о среднем значении — одна из теорем об определённом интеграле.
Формулировка[править | править код]
Пусть функция 
![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)



Тогда существует такое число 

.
Доказательство[править | править код]
Из неравенства 
.
Обозначив 
Так определённое число 

![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
Замечание[править | править код]
Если функция 
![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)

можно взять её наибольшее и наименьшее значения (которые, по теореме Вейерштрасса, достигаются),
тогда по теореме о промежуточном значении существует такая точка ![cin [a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b8df5ba00bbc02820be401c0dbc93d73392da8)

поэтому утверждение теоремы можно переписать в виде
.
Если воспользоваться формулой Ньютона-Лейбница, то это равенство запишется как
,
где 


Обобщение[править | править код]
Пусть функции 

![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)

а вторая из них не меняет знак (то есть либо всюду неотрицательна: 

Тогда существует такое число 

.
Доказательство[править | править код]
Пусть 
,
откуда, ввиду монотонности интеграла
.
Если 

и утверждение теоремы выполняется при любом 
В противном случае положим
.
Обобщение доказано. Если функция 
![cin [a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b8df5ba00bbc02820be401c0dbc93d73392da8)
(аналогично предыдущему).
Литература[править | править код]
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: Наука, 1969. — Т. II.
- Зорич В. А. Математический анализ. Ч. I. — М.: Наука, 1981.
5.
Оценка интеграла. Теорема о среднем
Укажем границы, между которыми наверняка заключено значение интеграла.
Теорема 7. (об
оценке
определенного
интеграла).
Значение
определенного
интеграла заключено между произведениями наименьшего и наибольшего значений
подынтегральной функции на длину интервала интегрирования, т. е.
Z b
m(b − a) ≤
f (x)dx ≤ M (b − a), a < b,
a
где m и M — соответственно наименьшее и наибольшее значения функции f (x) в
интервале [а,b]:
m ≤ f (x) ≤ M.
Доказательство. Возьмем две функции M − f (x) и m − f (x) . Первая из них в
интервале [a, b] неотрицательна, вторая неположительна. Значит, по теореме 6
Z b
Z b
[M − f (x)]dx ≥ 0,
[m − f ()]dx ≤ 0.
a
a
Применяя теоремы п. 3 и формулу
Rb
dx = b − a , получим
a
Z
Z
b
M (b − a) ≥
b
f (x)dx и m(b − a) ≤
a
f (x)dx.
a
что и требовалось доказать. Из доказательства теоремы 6 следует, что если только
функция f (x) не постоянная, то нестрогие неравенства можно заменить на строгие:
Z b
m(b − a) <
f (x)dx < M (b − a).
a
Находя границы для интеграла, мы, как говорят, производим его оценку. Может
случиться, что весьма трудно или даже невозможно найти точное значение интеграла,
а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода
оценками приходится довольно часто встречаться в математике.
Указанные в теореме 7 границы для интеграла тем более точны, чем короче интервал
интегрирования и чем меньше линия y = f (x) отличается по положению от прямой,
параллельной оси Ox .
Пример 1. Оценим интеграл
Z 2
5−x
dx.
2
0 9−x
Известными методами дифференциального исчисления находим, что наибольшее и
наименьшее значения подынтегральной функции в интервале [0,2] равны соответственно
y(2) = 0, 6 и y(2) = 0, 5 . Значит,
Z 2
5−x
dx < 0, 6(2 − 0),
0, 5(2 − 0) <
2
0 9−x
1
т. е. интеграл заключен между 1 и 1,2. Если считать, что он равен 1,1, то предельная
абсолютная ошибка равна 0,1, а относительная — 9%. Позже мы сумеем найти точное
значение приведенного интеграла. Оно равно 4/3 · ln 5 − ln 3 ≈ 1, 047 .
Пример 2. Оценим интеграл
Z π/2
sin x
dx.
x
π/4
Легко проверить, что подынтегральная функция в интервале [π/4, π/2] убывает и,
следовательно,
Z π/2
sin(π/2) π
sin x
sin(π/4) π
<
dx <
π/2 4
x
π/4 4
π/4
т. е.
√
Z π/2
1
sin x
2
<
dx <
.
2
x
2
π/4
Таким образом, интеграл заключен между 0,5 и 0,71, что дает нам право считать его
равным 0,6 с точностью до 0,1. Более точные приемы показывают, что приближенно он
равен 0,62.
Обобщение теоремы об оценке интеграла.
Интегрирование неравенств
Справедлива следующая более общая теорема, чем теорема 7.
Теорема 8. Если в каждой точке x интервала [a, b]
ψ(x) ≤ f (x) ≤ φ(x),
то
Z
Z
b
ψ(x)dx ≤
a
Z
b
b
f (x)dx ≤
a
φ(x)dx.
a
Это значит, что неравенство между функциями влечет неравенство того же
смысла между их определенными интегралами, или, говоря коротко, неравенства
можно интегрировать. Понятно хотя бы из простых геометрических соображений, что
дифференцирование неравенства может привести к нелепым результатам.
Доказательство теоремы немедленно следует из применения к неравенствам f (x) −
φ() ≤ 0 и f (x)−ψ(x) ≥ 0 теоремы 7 о знаке интеграла. Опять-таки знак равенства между
интегралами возможен только тогда, когда функции тождественно равны между собой.
В частном случае, когда φ(x) тождественно равно M , а ψ(x) тождественно равно
m , получаем теорему 7.
С помощью теоремы 8 легко получается важное неравенство, которым мы
воспользуемся в дальнейшем. При любом x
−|f (x)| ≤ f (x) ≤ |f (x)|.
(Если f (x) > 0 , то правая часть неравенства превращается в равенство, а левая часть
очевидна; если f (x) < 0 , то наоборот.) Тогда
Z b
Z b
Z b
−
|f (x)|dx ≤
f (x)dx ≤
|f (x)|dx,
a
a
a
2
или
Z
Z
b
|
b
f (x)dx| ≤
a
|f (x)|dx.
a
Модуль интеграла не превосходит интеграла от модуля функции. Предоставляем
читателю выяснить геометрический смысл этого неравенства. Напомним еще, что
аналогичное неравенство имеет место и для сумм: модуль суммы не превосходит суммы
модулей.
Теорема о среднем
Определенный интеграл обладает следующим важным свойством.
Теорема 9. (о среднем). Пусть функция f (x) непрерывна в замкнутом интервале [а,b].
Тогда внутри этого интервала существует хотя бы одно значение x = ξ , для которого
Rb
f (x)dx
a
= f (ξ).
(1)
b−a
Доказательство. Если функция f (x) постоянная, то формула (1) очевидна, причем
ξ — любая точка интервала [а,b]. Пусть теперь f (x) не постоянная, тогда в силу теоремы 7
имеем
Rb
f (x)dx
m< a
< M,
b−a
и, значит,
Rb
f (x)dx
a
= µ,
b−a
где µ — некоторое число, заключенное между наименьшим (m) и наибольшим (M )
значениями функции f (x) в интервале [a, b] .
В силу свойств непрерывных функций функция f (x) в каких-то двух точках
интервала [a, b] принимает значения m и и в какой-то точке, лежащей между ними,
принимает промежуточное значение µ . Значит, существует точка ξ ∈ (a, b) , в которой
f (ξ) = µ . Теорема доказана.
Из равенства (1) находим
Z
b
f (x)dx = f (ξ)(b − a), ξ ∈ (a, b).
a
Эта формула позволяет теорему о среднем сформулировать в такой форме:
Определенный интеграл от непрерывной функции равен произведению значения этой
функции в некоторой промежуточной точке интервала интегрирования на длину
интервала.
Среднее арифметическое значение функции
Определение 1. Средним арифметическим значением непрерывной функции y =
f (x) в интервале [а,b] называется отношение определенного интеграла от этой
функции к длине интервала:
Rb
f (x)dx
.
yc = a
b−a
3
На основании теоремы о среднем заключаем, что yc = f (ξ) , где ξ ∈ (a, b) . Среднее
значение непрерывной функции в замкнутом интервале всегда (если только функция не
постоянная) меньше некоторых ее значений, больше других ее значений и равно хотя бы
одному ее значению.
Понятие среднего значения функции очень употребительно в технике. Многие
величины часто характеризуются своими средними значениями, например: давление пара,
мощность переменного тока, скорость химической реакции и т. п.
4
In mathematics, the mean value theorem (or Lagrange theorem) states, roughly, that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints. It is one of the most important results in real analysis. This theorem is used to prove statements about a function on an interval starting from local hypotheses about derivatives at points of the interval.
More precisely, the theorem states that if 
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)






History[edit]
A special case of this theorem for inverse interpolation of the sine was first described by Parameshvara (1380–1460), from the Kerala School of Astronomy and Mathematics in India, in his commentaries on Govindasvāmi and Bhāskara II.[1] A restricted form of the theorem was proved by Michel Rolle in 1691; the result was what is now known as Rolle’s theorem, and was proved only for polynomials, without the techniques of calculus. The mean value theorem in its modern form was stated and proved by Augustin Louis Cauchy in 1823.[2] Many variations of this theorem have been proved since then.[3][4]
Formal statement[edit]
The function 



It is also possible that there are multiple tangents parallel to the secant.
Let ![{displaystyle f:[a,b]to mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




The mean value theorem is a generalization of Rolle’s theorem, which assumes 
The mean value theorem is still valid in a slightly more general setting. One only needs to assume that ![{displaystyle f:[a,b]to mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


exists as a finite number or equals 



Note that the theorem, as stated, is false if a differentiable function is complex-valued instead of real-valued. For example, define 

while 

These formal statements are also known as Lagrange’s Mean Value Theorem.[5]
Proof[edit]
The expression 





Define 


![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




By Rolle’s theorem, since 





Implications[edit]
Theorem 1: Assume that f is a continuous, real-valued function, defined on an arbitrary interval I of the real line. If the derivative of f at every interior point of the interval I exists and is zero, then f is constant in the interior.
Proof: Assume the derivative of f at every interior point of the interval I exists and is zero. Let (a, b) be an arbitrary open interval in I. By the mean value theorem,[6] there exists a point c in (a, b) such that
This implies that f(a) = f(b). Thus, f is constant on the interior of I and thus is constant on I by continuity. (See below for a multivariable version of this result.)
Remarks:
- Only continuity of f, not differentiability, is needed at the endpoints of the interval I. No hypothesis of continuity needs to be stated if I is an open interval, since the existence of a derivative at a point implies the continuity at this point. (See the section continuity and differentiability of the article derivative.)
- The differentiability of f can be relaxed to one-sided differentiability, a proof given in the article on semi-differentiability.
Theorem 2: If f’ (x) = g’ (x) for all x in an interval (a, b) of the domain of these functions, then f – g is constant, i.e. f = g + c where c is a constant on (a, b).
Proof: Let F = f − g, then F’ = f’ − g’ = 0 on the interval (a, b), so the above theorem 1 tells that F = f − g is a constant c or f = g + c.
Theorem 3: If F is an antiderivative of f on an interval I, then the most general antiderivative of f on I is F(x) + c where c is a constant.
Proof: It directly follows from the theorem 2 above.
Cauchy’s mean value theorem[edit]
Cauchy’s mean value theorem, also known as the extended mean value theorem,[7] is a generalization of the mean value theorem. It states: if the functions 

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


Geometrical meaning of Cauchy’s theorem
Of course, if 

Geometrically, this means that there is some tangent to the graph of the curve[8]
which is parallel to the line defined by the points 





which on the interval ![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)



Cauchy’s mean value theorem can be used to prove L’Hôpital’s rule. The mean value theorem is the special case of Cauchy’s mean value theorem when 
Proof of Cauchy’s mean value theorem[edit]
The proof of Cauchy’s mean value theorem is based on the same idea as the proof of the mean value theorem.
Generalization for determinants[edit]
Assume that 


![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
-
The mean value theorem displayed on a bridge in Beijing
There exists 

Notice that
and if we place 


The proof of the generalization is quite simple: each of 




Mean value theorem in several variables[edit]
The mean value theorem generalizes to real functions of multiple variables. The trick is to use parametrization to create a real function of one variable, and then apply the one-variable theorem.
Let 







for some 



where 


In particular, when the partial derivatives of 

As an application of the above, we prove that 








for every 





The above arguments are made in a coordinate-free manner; hence, they generalize to the case when 
Mean value theorem for vector-valued functions[edit]
There is no exact analog of the mean value theorem for vector-valued functions (see below). However, there is an inequality which can be applied to many of the same situations to which the mean value theorem is applicable in the one dimensional case:[9]
The theorem follows from the mean value theorem. Indeed, take 

for some 


If 


Jean Dieudonné in his classic treatise Foundations of Modern Analysis discards the mean value theorem and replaces it by mean inequality (which is given below) as the proof is not constructive and one cannot find the mean value and in applications one only needs mean inequality. Serge Lang in Analysis I uses the mean value theorem, in integral form, as an instant reflex but this use requires the continuity of the derivative. If one uses the Henstock–Kurzweil integral one can have the mean value theorem in integral form without the additional assumption that derivative should be continuous as every derivative is Henstock–Kurzweil integrable.
The reason why there is no analog of mean value equality is the following: If f : U → Rm is a differentiable function (where U ⊂ Rn is open) and if x + th, x, h ∈ Rn, t ∈ [0, 1] is the line segment in question (lying inside U), then one can apply the above parametrization procedure to each of the component functions fi (i = 1, …, m) of f (in the above notation set y = x + h). In doing so one finds points x + tih on the line segment satisfying
But generally there will not be a single point x + t*h on the line segment satisfying
for all i simultaneously. For example, define:
Then 



![{displaystyle left[0,2pi right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecbccc3195ac7ed59d31ec366dbd75739b85e1d3)
The above theorem implies the following:
In fact, the above statement suffices for many applications and can be proved directly as follows. (We shall write 







We want to show 








Let 












Since 




![{displaystyle [a',b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2199a20ce14a38267ad303f042837644e8feb46)
since 


For some applications of mean value inequality to establish basic results in calculus, see also Calculus on Euclidean space#Basic notions.
A certain type of generalization of the mean value theorem to vector-valued functions is obtained as follows: Let f be a continuously differentiable real-valued function defined on an open interval I, and let x as well as x + h be points of I. The mean value theorem in one variable tells us that there exists some t* between 0 and 1 such that
On the other hand, we have, by the fundamental theorem of calculus followed by a change of variables,
Thus, the value f′(x + t*h) at the particular point t* has been replaced by the mean value
This last version can be generalized to vector valued functions:
Proposition — Let U ⊂ Rn be open, f : U → Rm continuously differentiable, and x ∈ U, h ∈ Rn vectors such that the line segment x + th, 0 ≤ t ≤ 1 remains in U. Then we have:
where Df denotes the Jacobian matrix of f and the integral of a matrix is to be understood componentwise.
Proof. Let f1, …, fm denote the components of f and define:
Then we have
The claim follows since Df is the matrix consisting of the components 

The mean value inequality can then be obtained as a corollary of the above proposition (though under the assumption the derivatives are continuous).[11]
Cases where the theorem cannot be applied[edit]
Both conditions for the mean value theorem are necessary:
- f(x) is differentiable on (a,b)
- f(x) is continuous on [a,b]
Where one of the above conditions is not satisfied, the mean value theorem is not valid in general, and so it cannot be applied.
Function is differentiable on open interval a,b[edit]
The necessity of the first condition can be seen by the counterexample where the function 
Function is continuous on closed interval a,b[edit]
The necessity of the second condition can be seen by the counterexample where the function ![{displaystyle f(x)={begin{cases}1,&{text{at }}x=0\0,&{text{if }}xin (0,1]end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cb6e79196b3cfc68f23749dc33e5c9d7c878cfe)



But not criteria 2 since 



Mean value theorems for definite integrals[edit]
First mean value theorem for definite integrals[edit]
Geometrically: interpreting f(c) as the height of a rectangle and b–a as the width, this rectangle has the same area as the region below the curve from a to b[12]
Let f : [a, b] → R be a continuous function. Then there exists c in (a, b) such that
Since the mean value of f on [a, b] is defined as
we can interpret the conclusion as f achieves its mean value at some c in (a, b).[13]
In general, if f : [a, b] → R is continuous and g is an integrable function that does not change sign on [a, b], then there exists c in (a, b) such that
Proof that there is some c in [a, b][14][edit]
Suppose f : [a, b] → R is continuous and g is a nonnegative integrable function on [a, b]. By the extreme value theorem, there exists m and M such that for each x in [a, b], 
![{displaystyle f[a,b]=[m,M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e3c8c0b2601b0d35f20941e21d0d3812086e54b)
Now let
If 
means
so for any c in (a, b),
If I ≠ 0, then
By the intermediate value theorem, f attains every value of the interval [m, M], so for some c in [a, b]
that is,
Finally, if g is negative on [a, b], then
and we still get the same result as above.
QED
Second mean value theorem for definite integrals[edit]
There are various slightly different theorems called the second mean value theorem for definite integrals. A commonly found version is as follows:
- If G : [a, b] → R is a positive monotonically decreasing function and φ : [a, b] → R is an integrable function, then there exists a number x in (a, b] such that
Here 

- If G : [a, b] → R is a monotonic (not necessarily decreasing and positive) function and φ : [a, b] → R is an integrable function, then there exists a number x in (a, b) such that
Mean value theorem for integration fails for vector-valued functions[edit]
If the function 

For example, consider the following 2-dimensional function defined on an 
Then, by symmetry it is easy to see that the mean value of 
However, there is no point in which 

A probabilistic analogue of the mean value theorem[edit]
Let X and Y be non-negative random variables such that E[X] < E[Y] < ∞ and 
Let g be a measurable and differentiable function such that E[g(X)], E[g(Y)] < ∞, and let its derivative g′ be measurable and Riemann-integrable on the interval [x, y] for all y ≥ x ≥ 0. Then, E[g′(Z)] is finite and[16]
Mean value theorem in complex variables[edit]
As noted above, the theorem does not hold for differentiable complex-valued functions. Instead, a generalization of the theorem is stated such:[17]
Let f : Ω → C be a holomorphic function on the open convex set Ω, and let a and b be distinct points in Ω. Then there exist points u, v on the interior of the line segment from a to b such that
Where Re() is the real part and Im() is the imaginary part of a complex-valued function.
See also: Voorhoeve index.
See also[edit]
- Newmark-beta method
- Mean value theorem (divided differences)
- Racetrack principle
- Stolarsky mean
Notes[edit]
- ^ J. J. O’Connor and E. F. Robertson (2000). Paramesvara, MacTutor History of Mathematics archive.
- ^ Ádám Besenyei. “Historical development of the mean value theorem” (PDF).
- ^ Lozada-Cruz, German (2020-10-02). “Some variants of Cauchy’s mean value theorem”. International Journal of Mathematical Education in Science and Technology. 51 (7): 1155–1163. Bibcode:2020IJMES..51.1155L. doi:10.1080/0020739X.2019.1703150. ISSN 0020-739X. S2CID 213335491.
- ^ Sahoo, Prasanna. (1998). Mean value theorems and functional equations. Riedel, T. (Thomas), 1962-. Singapore: World Scientific. ISBN 981-02-3544-5. OCLC 40951137.
- ^ a b c Kirshna’s Real Analysis: (General). Krishna Prakashan Media.
- ^ “Mean Value Theorem”. keepnotes.com.
- ^ W., Weisstein, Eric. “Extended Mean-Value Theorem”. mathworld.wolfram.com. Retrieved 2018-10-08.
- ^ “Cauchy’s Mean Value Theorem”. Math24. Retrieved 2018-10-08.
- ^ Rudin, Walter (1976). Principles of Mathematical Analysis (3rd ed.). New York: McGraw-Hill. p. 113. ISBN 978-0-07-054235-8. Theorem 5.19.
- ^ Hörmander 2015, Theorem 1.1.1. and remark following it.
- ^
Lemma — Let v : [a, b] → Rm be a continuous function defined on the interval [a, b] ⊂ R. Then we have
Proof. Let u in Rm denote the value of the integral
Now we have (using the Cauchy–Schwarz inequality):
Now cancelling the norm of u from both ends gives us the desired inequality.
Mean Value Inequality — If the norm of Df(x + th) is bounded by some constant M for t in [0, 1], then
Proof.
- ^ “Mathwords: Mean Value Theorem for Integrals”. www.mathwords.com.
- ^ Michael Comenetz (2002). Calculus: The Elements. World Scientific. p. 159. ISBN 978-981-02-4904-5.
- ^ Editorial note: the proof needs to be modified to show there is a c in (a, b)
- ^ Hobson, E. W. (1909). “On the Second Mean-Value Theorem of the Integral Calculus”. Proc. London Math. Soc. S2–7 (1): 14–23. Bibcode:1909PLMS…27…14H. doi:10.1112/plms/s2-7.1.14. MR 1575669.
- ^ Di Crescenzo, A. (1999). “A Probabilistic Analogue of the Mean Value Theorem and Its Applications to Reliability Theory”. J. Appl. Probab. 36 (3): 706–719. doi:10.1239/jap/1032374628. JSTOR 3215435. S2CID 250351233.
- ^ 1 J.-Cl. Evard, F. Jafari, A Complex Rolle’s Theorem, American Mathematical Monthly, Vol. 99, Issue 9, (Nov. 1992), pp. 858-861.
References[edit]
- Hörmander, Lars (2015), The Analysis of Linear Partial Differential Operators I: Distribution Theory and Fourier Analysis, Classics in Mathematics (2nd ed.), Springer, ISBN 9783642614972
External links[edit]
- “Cauchy theorem”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- PlanetMath: Mean-Value Theorem
- Weisstein, Eric W. “Mean value theorem”. MathWorld.
- Weisstein, Eric W. “Cauchy’s Mean-Value Theorem”. MathWorld.
- “Mean Value Theorem: Intuition behind the Mean Value Theorem” at the Khan Academy
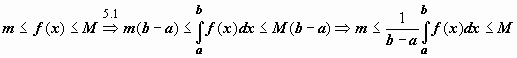
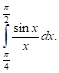
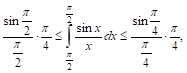
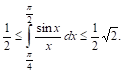
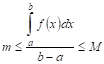
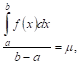
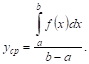





















![{displaystyle {begin{cases}[a,b]to mathbb {R} ^{2}\tmapsto (f(t),g(t))end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/035d912ebe2e72e28cf8922a39d1b07ee8afe321)












![{displaystyle {begin{cases}f:[0,2pi ]to mathbb {R} ^{2}\f(x)=(cos(x),sin(x))end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/537a6776144419319a90c743f3bfa85384551b8e)








![{displaystyle {begin{cases}g_{i}:[0,1]to mathbb {R} \g_{i}(t)=f_{i}(x+th)end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3578b3a55c366cbcab9cd1677a9f4e5720009492)
















![{displaystyle {begin{cases}G:[0,2pi ]^{n}to mathbb {R} ^{2}\G(x_{1},dots ,x_{n})=left(sin(x_{1}+cdots +x_{n}),cos(x_{1}+cdots +x_{n})right)end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313681274f21ab3d719858b7eee2f8fed7307df7)
![{displaystyle int _{[0,2pi ]^{n}}G(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}=(0,0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/800b9da34869b8de54b9e67e50211354ff1230c9)
![{displaystyle f_{Z}(x)={Pr(Y>x)-Pr(X>x) over {rm {E}}[Y]-{rm {E}}[X]},,qquad xgeqslant 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98380bb043d37ca11885348245ab1f1e05019170)
![{rm {E}}[g(Y)]-{rm {E}}[g(X)]={rm {E}}[g'(Z)],[{rm {E}}(Y)-{rm {E}}(X)].](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d3a485925f91f6271a2201cc6cc46b4d5d381f6)







