Как найти среднее значение по стажу

Средней
величиной
называется обобщенный показатель,
характеризующий типичный уровень
варьирующего количественного признака
на единицу совокупности в определенных
условиях места и времени. Средний
показатель отражает то общее,
что характерно (типично) для всех единиц
изучаемой совокупности, в то же время
он игнорирует различия отдельных единиц
совокупности.

Замена
множества различных индивидуальных
значений признака средним
показателем позволяет выявить
закономерности, присущие массовым
явлениям, которые незаметны в единичных.
Объективность и типичность статистической
средней обеспечивается соблюдением
условий:

• средняя
  должна вычисляться для качественно
  однородной совокупности, для чего
  необходима группировка данных;

• для
  исчисления средних должны быть
  использованы массовые данные.

Средняя
величина всегда именованная, она имеет
ту же размерность, что и признак у
отдельных единиц совокупности. В
экономических исследованиях и плановых
расчетах применяются 2 категории средних:

• степенные
  средние: средняя гармоническая, средняя
  геометрическая, средняя арифметическая,
  средняя квадратическая;

• структурные
  средние:
  мода, медиана.

Степенные
средние связаны неравенством:
.

Средняя
арифметическая (простая)
определяется формулой:
.

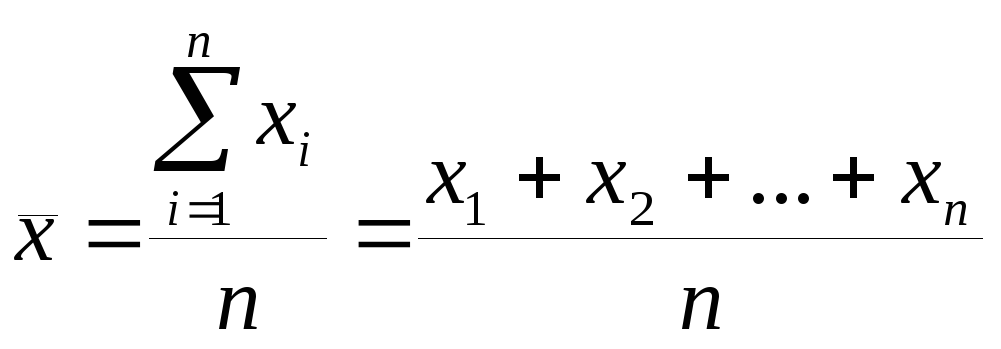Для
сгруппированных величин используется
средняя арифметическая взвешенная:

.

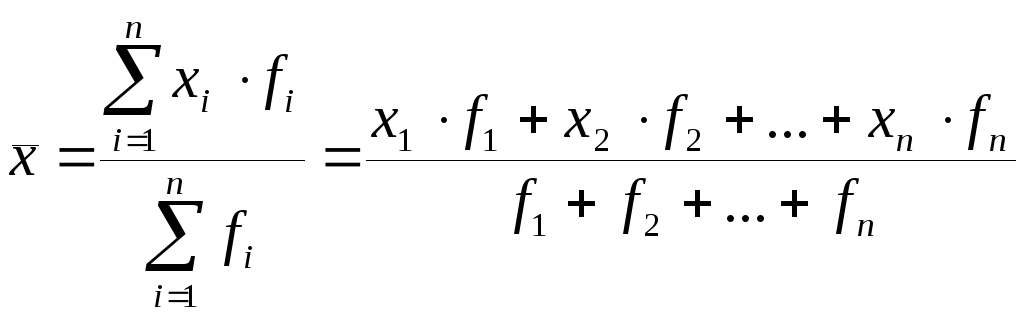Дано:
имеется распределение рабочих участка
по стажу работы:

Таблица
7

Стаж работы, лет	до 5 лет	5 – 10	10 – 15	15 – 20
Количество рабочих	2	6	15	7

Найти:
средний
стаж рабочих участка.

Решение:

• Для
  каждого интервала рассчитывается
  среднее значение признака как полусумма
  нижнего и верхнего значений интервала:

• для
  1 интервала:
  ,

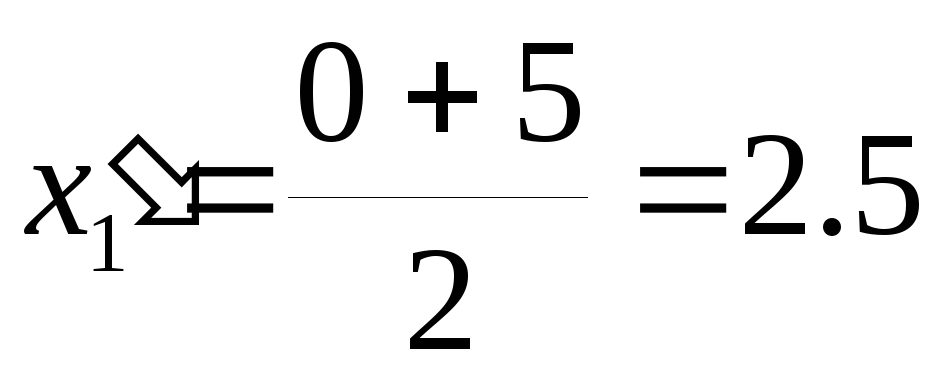• для
  2 интервала:
  ,

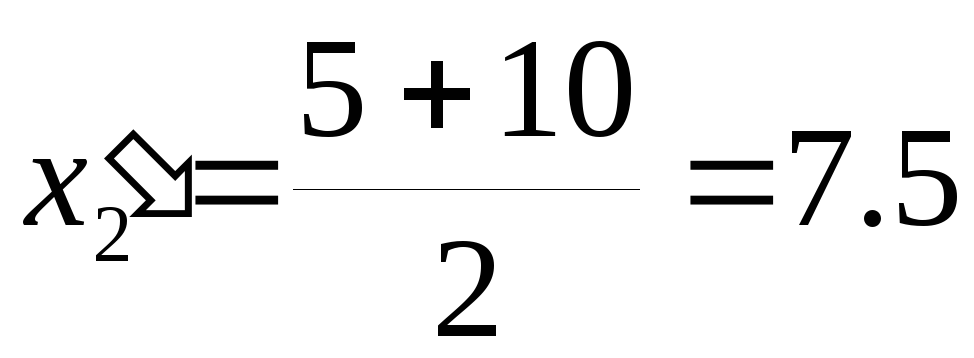• для
  3 интервала:
  ,

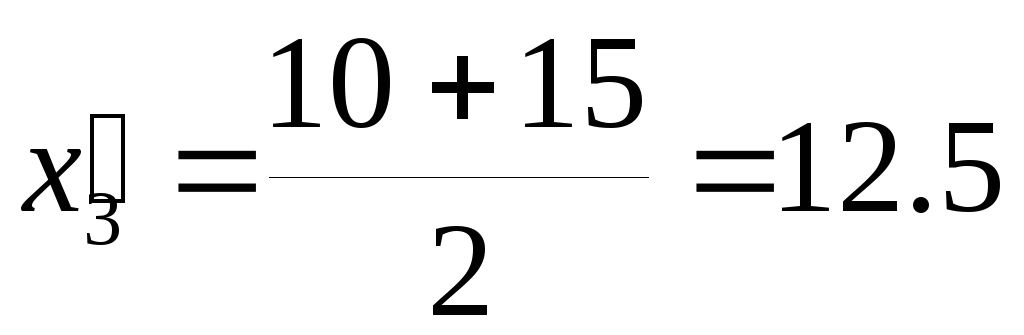• для
  4 интервала:
  .

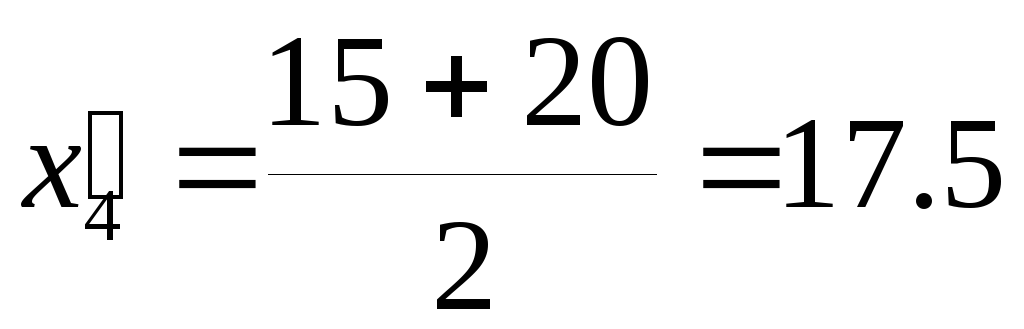• По
  формуле средней взвешенной рассчитывается
  средний стаж работы:

(лет)
[4].

1. Перейти
   на чистый лист.

2. Для
   автоматизированного расчета результатов
   решения задачи в ячейки А1:А3
   соответственно
   ввести: Стаж,
   работы,
   Количество.
   В ячейки В1:В2
   соответственно
   ввести:
   0,
   5;
   в ячейки С1:С2
   числа:
   5,
   10;
   в ячейки D1:D2
   ввести: 10,
   15
   и в ячейки E1:E2
   ввести: 15,
   20.
   В ячейки B3:E3
   ввести
   числа, соответствующие количеству
   рабочих в интервалах по стажу: 2,
   6,
   15,
   7
   и
   выделить их цветом и границами обрамления.

3. В
   ячейку А5
   ввести Полусумма,
   в ячейку В5
   (используя мастер функций) ввести
   формулу, подсчитывающую полусумму
   значений интервала по стажу =СРЗНАЧ(B1:B2).

4. Установить
   курсор в правый нижний угол ячейки В5,
   когда
   он примет крестообразный вид, нажать
   и, удерживая нажатой левую кнопку мыши,
   протянуть его в ячейку Е5
   (тем самым копируя формулу для подсчета
   среднего значения для других интервалов).
   Выделить ячейки цветом и границами
   обрамления.

5. В
   ячейки G1
   и G2
   соответственно
   ввести Средний
   и
   Стаж.
   В ячейку G3
   (используя мастер функций) ввести
   формулу, рассчитывающую средний стаж
   работы в целом по участку,
   =СУММПРОИЗВ(B3:E3;B5:E5)/СУММ(B3:E3).
   Выделить ячейки цветом и границами
   обрамления.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задача 1. По следующим данным определите средний стаж рабочего (табл.4.5):

Общий стаж работы, лет	до 5	5-10	10-15	15-20	20-25	25 и более	Итого
Число рабочих

Решение. Признаком в данной задаче является общий стаж рабочего, а частотами соответственно количество рабочих, имеющих тот или иной стаж. Ряд распределения — интервальный, причем первый и последний интервал — открытые.

Если интервалы открыты, то по правилам принимаем величину первого интервала равной второму, а последнего предпоследнему. Так как имеются и значения признака и частоты, то средний стаж находим по формуле средней арифметической взвешенной. А так как ряд интервальный, то в качестве значения признака в каждой группе берём середины интервала

.

Задача 2. Все частоты уменьшились в два раза, а все варианты увеличились на две единицы. Что произойдет со средней?

Решение. Согласно свойствам средней арифметической, если все частоты ряда уменьшить или увеличить в одинаковое количество раз, то средняя не изменится, т.е. с точки зрения частот — средняя не изменится. Если все варианты увеличить или уменьшить на одно и то же число, то и средняя изменится на это же число. В нашем случае средняя увеличится на две единицы.

Задача 3. Двое рабочих в течение 8-часового рабочего дня изготовляют одни и те же детали. Первый из них тратит на изготовление детали 30 мин., второй — 40 мин. Вычислите среднюю затрату времени на изготовление одной детали.

Решение. В этой задаче явно даны только значения признака — затраты времени, а частоты, которыми является количество изготовленных каждым рабочим деталей, в явном виде не присутствуют. Однако произведения значений признака на частоты дает количество проработанного времени — 8 час. Так как произведения признака на частоту равны, то средняя определяется по формуле средней гармонической простой:

мин.

Задача 4. Автомобиль проехал 1000 км, из них 480 км он прошел со скоростью 60 км/час, 320 — со скоростью 80 км/час и 200 км — со скоростью 50 км/час. Определите среднюю скорость, с которой совершался рейс.

Решение. В этой задаче опять известны только значения признака, а значения частот (время) не даны, однако имеются данные о пройденном расстоянии, которое является произведением признака на частоту. В этом случае средняя рассчитывается по формуле средней гармонической взвешенной:

км/ч.

Задача 5. Определите среднегодовой темп роста выпуска продукции на заводе, если в 1990 г. было произведено продукции на 21,15 у.д.е., а в 1995 г. было запланировано произвести продукции на 35 у.д.е.

Решение. Для определения средних темпов роста применяется средняя геометрическая. Когда имеются данные о первом периоде (в нашем случае — выпуск продукции в 1990 г. на сумму 21,15 у.д.е.) и в последнем периоде (в задаче — выпуск продукции по плану в 1995 г. на сумму 35 у.д.е.), среднегодовой темп роста определяется по формуле:

Задача 6. Определить моду и медиану по следующим данным (табл. 4.6):

Распределение студентов заочного отделения по возрасту

Возрастные группы	Число студентов	Накопленные частоты
до 20 лет
20-25
25-30
30-35
35-40
40-45
45 лет и выше
Итого:

Решение. Для определения моды определяем модальный интервал. Им является интервал 25-30 лет, так как его частота наибольшая (1054), тогда

Мо лет.

Для определения медианы тоже необходимо определить медианный интервал. Медианным интервалом является интервал 25-30, так как он является первым интервалом, накопленная частота которого превышает полусумму частот (3462: 2=1731). Тогда медиана определится как:

Ме года.

РАЗДЕЛ 5. ПОКАЗАТЕЛИ ВАРИАЦИИ И ДРУГИЕ ХАРАКТЕРИСТИКИ РЯДОВ РАСПРЕДЕЛЕНИЯ

5.1. Понятие о вариации

При изучении процессов и явлений общественной жизни статистика встречается с разнообразной вариацией признаков, характеризующей отдельные единицы совокупности. Величина признака изменяется, колеблется под влиянием различных причин и условий. Чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация.

Дневная выработка рабочих двух бригад

Номер бригады	Число рабочих	Дневная выработка деталей отдельных рабочих, шт.	Средняя дневная выработка
75 90 78 82 93 86
65 122 84 70 105 58

Одна и та же средняя может характеризовать совокупность, в которой размеры вариации признака существенно отличаются друг от друга (табл.5.1). Как видно, средняя дневная выработка в обеих бригадах одинакова, хотя в первой бригаде средняя значительно меньше отличается от индивидуальных значений признака, чем во второй.

Следовательно, для всесторонней характеристики рядов распределения необходимы показатели, определяющие меру, степень колеблемости отдельных значений признака от средней, т.е. степень вариации, а также форму (тип) распределения, характеризующую ее закономерности.

5.2. Показатели вариации и способы их расчета

а) Размах вариации является наиболее простой мерой колеблемости значений признака и представляет собой разность между максимальным и минимальным значением признака: R = Х_max — Х_min.

Размах вариации имеет недостаток, проявляющийся в том, что при вычислении R используется только крайние значения ряда распределения, и он не всегда правильно характеризует колеблемость признака.

В связи с тем, что каждое индивидуальное значение признака отклоняется от средней на определенную величину, мерой вариации может служить средняя из отклонений каждой отдельной варианты от их средней.

Такими показателями являются среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

б)Среднее линейное отклонение представляет собой среднюю из абсолютных значений отклонений индивидуальных значений признаков от их средней:

; .

Недостаток среднего линейного отклонения в том, что оно берется без учета знака. Поэтому в статистике чаще используют дисперсию и среднее квадратическое отклонение.

в) Дисперсия и среднее квадратическое отклонение. Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины

; .

Дисперсия имеет очень большое значение в анализе. Однако ее применение как меры вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. Поэтому вычисляют среднее квадратическое отклонение, равное корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии

.

Сопоставление линейных или средних квадратических отклонений по нескольким совокупностям дает возможность определять степень их однородности в отношении того или иного признака. Чем меньше:R, d, σ 2 ,σ, тем совокупность более однородна, тем более типичной будет средняя величина.

г) Коэффициент вариации. Так как дисперсия и среднее квадратическое отклонение характеризуют абсолютный размер отклонений, то представляет интерес сопоставить среднее квадратическое отклонение с его средней величиной. Такой показатель называется коэффициентом вариации

.

Если взять отношение среднего линейного отклонения к средней арифметической, то получим линейный коэффициент вариации .

Отношение размаха вариации к средней арифметической называется коэффициентом осцилляции: .

Не нашли то, что искали? Воспользуйтесь поиском:

Понятие и виды средних величин

Средняя величина — это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.

Существует 2 класса средних величин: степенные и структурные.

К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.

Степенные средние величины

Степенные средние могут быть простыми и взвешенными.

Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:

Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:

где X – значения отдельных статистических величин или середин группировочных интервалов;
m — показатель степени, от значения которого зависят следующие виды степенных средних величин:
при m = -1 средняя гармоническая;
при m = 0 средняя геометрическая;
при m = 1 средняя арифметическая;
при m = 2 средняя квадратическая;
при m = 3 средняя кубическая.

Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.

Средняя арифметическая

Средняя арифметическая — это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

где X — значения величин, для которых необходимо рассчитать среднее значение; N — общее количество значений X (число единиц в изучаемой совокупности).

Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.

Средняя арифметическая взвешенная имеет следующий вид:

где f — количество величин с одинаковым значением X (частота).

Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.

Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.

Например, на предприятии 10 работников со стажем работы до 3 лет, 20 — со стажем от 3 до 5 лет, 5 работников — со стажем более 5 лет. Тогда рассчитаем средний стаж работников по формуле средней арифметической взвешенной, приняв в качестве X середины интервалов стажа (2, 4 и 6 лет):
(2*10+4*20+6*5)/(10+20+5) = 3,71 года.

Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.

Средняя гармоническая

Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:

Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:

Например, автомобиль ехал из пункта А в пункт Б со скоростью 90 км/ч, а обратно — со скоростью 110 км/ч. Для определения средней скорости применим формулу средней гармонической простой, так как в примере дано расстояние w₁=w₂ (расстояние из пункта А в пункт Б такое, же как и из Б в А), которое равно произведению скорости (X) на время (f). Средняя скорость = (1+1)/(1/90+1/110) = 99 км/ч.

Средняя геометрическая

Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.

Например, в период с 2005 по 2008 годы индекс инфляции в России составлял: в 2005 году — 1,109; в 2006 — 1,090; в 2007 — 1,119; в 2008 — 1,133. Так как индекс инфляции — это относительное изменение (индекс динамики), то рассчитывать среднее значение нужно по средней геометрической: (1,109*1,090*1,119*1,133)^(1/4) = 1,1126, то есть за период с 2005 по 2008 ежегодно цены росли в среднем на 11,26%. Ошибочный расчет по средней арифметической дал бы неверный результат 11,28%.

Средняя квадратическая

Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.

Главной сферой применения квадратической средней является измерение вариации значений X, о чем пойдет речь позднее в этой лекции.

Средняя кубическая

Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.

Структурные средние величины

К наиболее часто используемым структурным средним относятся статистическая мода и статистическая медиана.

Статистическая мода

Статистическая мода — это наиболее часто повторяющееся значение величины X в статистической совокупности.

Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) или мультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.

Например, на предприятии работает 16 человек: 4 из них — со стажем 1 год, 3 человека — со стажем 2 года, 5 — со стажем 3 года и 4 человека — со стажем 4 года. Таким образом, модальный стаж Мо=3 года, поскольку частота этого значения максимальна (f=5).

Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:

где Мо – мода;
Х_НМо – нижняя граница модального интервала;
h_Мо – размах модального интервала (разность между его верхней и нижней границей);
f_Мо – частота модального интервала;
f_Мо-1 – частота интервала, предшествующего модальному;
f_Мо+1 – частота интервала, следующего за модальным.

Например, на предприятии 10 работников со стажем работы до 3 лет, 20 — со стажем от 3 до 5 лет, 5 работников — со стажем более 5 лет. Рассчитаем модальный стаж работы в модальном интервале от 3 до 5 лет: Мо = 3 + 2*(20-10)/(2*20-10-5) = 3,8 (года).

Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.

Статистическая медиана

Статистическая медиана – это значение величины X, которое делит упорядоченную по возрастанию или убыванию статистическую совокупность на 2 равных по численности части. В итоге у одной половины значение больше медианы, а у другой — меньше медианы.

Если X задан дискретно, то для определения медианы все значения нумеруются от 0 до N в порядке возрастания, тогда медиана при четном числе N будет лежать посередине между X c номерами 0,5N и (0,5N+1), а при нечетном числе N будет соответствовать значению X с номером 0,5(N+1).

Например, имеются данные о возрасте студентов-заочников в группе из 10 человек — X: 18, 19, 19, 20, 21, 23, 23, 25, 28, 30 лет. Эти данные уже упорядочены по возрастанию, а их количество N=10 — четное, поэтому медиана будет находиться между X с номерами 0,5*10=5 и (0,5*10+1)=6, которым соответствуют значения X₅=21 и X₆=23, тогда медиана: Ме = (21+23)/2 = 22 (года).

Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:

где Ме – медиана;
Х_НМе – нижняя граница медианного интервала;
h_Ме – размах медианного интервала (разность между его верхней и нижней границей);
f_Ме – частота медианного интервала;
f_Ме-1 – сумма частот интервалов, предшествующих медианному.

В ранее рассмотренном примере при расчете модального стажа (на предприятии 10 работников со стажем работы до 3 лет, 20 — со стажем от 3 до 5 лет, 5 работников — со стажем более 5 лет) рассчитаем медианный стаж. Половина общего числа работников составляет (10+20+5)/2 = 17,5 и находится в интервале от 3 до 5 лет, а в первом интервале до 3 лет — только 10 работников, а в первых двух — (10+20)=30, что больше 17,5, значит интервал от 3 до 5 лет — медианный. Внутри него определяем условное значение медианы: Ме = 3+2*(0,5*30-10)/20 = 3,5 (года).

Также как и в случае с модой, при определении медианы если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.

Показатели вариации

Вариация — это различие значений величин X у отдельных единиц статистической совокупности. Для изучения силы вариации рассчитывают следующие показатели вариации: размах вариации, среднее линейное отклонение, линейный коэффициент вариации, дисперсия, среднее квадратическое отклонение, квадратический коэффициент вариации.

Размах вариации

Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:

Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.

Cреднее линейное отклонение

Cреднее линейное отклонение — это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой — получим среднее линейное отклонение простое:

Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.

Если исходные данные X сгруппированы (имеются частоты f), то расчет среднего линейного отклонения выполняется по формуле средней арифметической взвешенной — получим среднее линейное отклонение взвешенное:

Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.

Линейный коэффициент вариации

Линейный коэффициент вариации — это отношение среднего линейного отклонение к средней арифметической:

С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.

В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, линейный коэффициент вариации составит 0,5/4 = 0,125 или 12,5%.

Дисперсия

Дисперсия — это средний квадрат отклонений значений X от среднего арифметического значения. Дисперсию можно рассчитывать по формуле средней арифметической простой — получим дисперсию простую:

В уже знакомом нам примере про студента, который сдал 4 экзамена и получил оценки: 3, 4, 4 и 5, ранее уже была рассчитана средняя арифметическая = 4. Тогда дисперсия простая Д = ((3-4) 2 +(4-4) 2 +(4-4) 2 +(5-4) 2 )/4 = 0,5.

Если исходные данные X сгруппированы (имеются частоты f), то расчет дисперсии выполняется по формуле средней арифметической взвешенной — получим дисперсию взвешенную:

В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию взвешенную: Д = ((3-4) 2 *1+(4-4) 2 *2+(5-4) 2 *1)/4 = 0,5.

Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:

В уже знакомом нам примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию методом разности средней квадратов и квадрата средней:
Д = (3 2 *1+4 2 *2+5 2 *1)/4-4 2 = 16,5-16 = 0,5.

Если значения X — это доли совокупности, то для расчета дисперсии используют частную формулу дисперсии доли:

.

Cреднее квадратическое отклонение

Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:

Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:

В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее: .

Квадратический коэффициент вариации

Квадратический коэффициент вариации — это самый популярный относительный показатель вариации:

Критериальным значением квадратического коэффициента вариации V служит 0,333 или 33,3%, то есть если V меньше или равен 0,333 — вариация считает слабой, а если больше 0,333 — сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина — нетипичной и ее нельзя использовать как обобщающий показатель этой совокупности.

В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.

• 
• 
• 

• Редизайн сайта мебели
• Разработка сайта услуг
• Редизайн сайта эвакуации

Для компаний полезно знать, как долго в среднем работают их сотрудники. Высокие значения среднего непрерывного стажа персонала обычно говорят о лояльности и уважении сотрудников к своей компании. Длительный стаж способствует снижению затрат на обучение и дополнительный наем персонала.

Ключевой вопрос, на который помогает ответить этот показатель — как долго наши сотрудники остаются лояльными по отношению к нашей компании?

Рассматриваемый ключевой показатель эффективности (КПЭ) дает понимание об уровне удовлетворенности персонала своим местом работы. Для оценки конкурентных преимуществ компании значение данного КПЭ можно сравнивать с аналогичными значениями компаний-лидеров в своей отрасли. Средний стаж непрерывной работы может рассчитываться как по отношению ко всему персоналу компании, так и по отношению к определенной категории сотрудников.

Как проводить измерения

Метод сбора информации

Данные для рассматриваемого КПЭ поступают из системы кадрового учета и включают сведения о дате поступления на работу каждого сотрудника и длительности его работы в компании.

Формула

Средний стаж непрерывной работы = Суммарный стаж всех штатных сотрудников / Общее количество штатных сотрудников

Средний стаж непрерывной работы сотрудников определенной категории = Суммарный стаж этих сотрудников / Общее количество сотрудников определенной категории

Данный показатель необходимо рассчитывать ежегодно или каждые шесть месяцев.
Источником данных служит система кадрового учета.
Так как данные предоставляются внешним поставщиком, их стоимость для вас равна нулю.

Целевые значения

Целевые значения могут быть основаны на обобщенных величинах. Последние данные (за 2010 г.), опубликованные Бюро по трудовой статистике США, показывают, что средний стаж наемных рабочих и служащих на одном месте составляет 4,4 года (4,6 года для муж чин и 4,2 года для женщин). Данные также показывают, что 29% работников в возрасте 16 лет и старше имеют стаж работы на одном месте 10 и более лет. Однако существует значительная разница и зависимости от отрасли, и, например, показатель среднего стажа работы в колл-центрах и гостиничном бизнесе заметно ниже, чем в других отраслях.

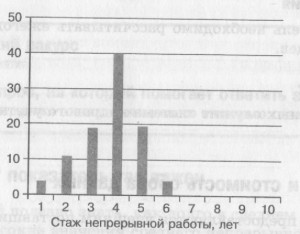
Пример. В качестве примера рассмотрим инжиниринговую компанию, чей штат насчитывает 100 человек. Распределение стажа соответствует представленному на рисунке и составляет: четыре человека со стажем в один год, 11 человек со стажем два года, 19 человек со стажем три года, 40 человек со стажем четыре года, 20 человек со стажем пять лет, четыре человека со стажем шесть лет, один человек со стажем но семь лет и один человек со стажем десять лет.

Средний непрерывный стаж = ((4 × 1)+ (11 × 2)+ (19 × 3)+ (40 × 4)+ (20 × 5)+ (4 × 6)+ (1 × 8)+ (1 × 10)) / 100 = 3,85 года

Замечания

Продолжительный средний стаж может также свидетельствовать о самоуспокоенности и расслабленности сотрудников, об отсутствии свежих идей в компании. Вот почему данный показатель необходимо анализировать совместно с показателем текучести кадров для более детального понимания ситуации.

Некоторые работники возвращаются в прежние компании после работы в других организациях. В этом случае расчет можно вести либо не учитывая предыдущий период работы, либо суммируя все периоды работы в компании. С точки зрения стратегии, последний подход более предпочтителен.

Определите средний стаж работы работников и его модальный и медианный уровни, а также квартили

---

Подборка по базе: тема 5 задача номер 1 прокурорский надзор.docx, Практическая работа_Исправлена 3 задачаповтор.docx, Оценка рисков. Задача 2..docx, Билет 5 задача 2.doc, В3 задача 4.doc, Бадмажапова П2005, задача.docx, Кейсовая задача.docx, Кейс задача №1 ПРАВО.docx, Контрольный вопрос и задача лаб-13.docx, УП МОЯ Задача 4.docx

---

Задача №22
В результате 10%-ного механического выборочного обследования работников предприятия получены данные о трудовом стаже:

Группы работников по стажу работы, лет	Число работников
До 5 5-10 10-15 15-20 20 и более	3 8 20 12 7
Итого	50

Определите:

1. средний стаж работы обследуемых работников (выборочную среднюю);
2. дисперсию и среднее квадратическое отклонение стажа работы;
3. коэффициент вариации;
4. с вероятностью 0,954 предельную ошибку выборки и интервал, в котором находится средний стаж работы всех работников предприятия.

Сделайте выводы.
Решение:

Для расчетов заменим интервалы их средними значениями. Величины первого и последнего открытых интервалов условно примем равными величинам второго и предпоследнего интервалов соответственно. Заполним вспомогательную расчетную таблицу:

Группы работников по стажу работы, лет	Число работников f	Среднее значение интервала, x	x⋅f	x2⋅f
до 5	3	2,5	7,5	18,75
5-10	8	7,5	60	450
10-15	20	12,5	250	3125
15-20	12	17,5	210	3675
20 и более	7	22,5	157,5	3543,75
Итого	50		685	10812,5

1. Рассчитаем среднее значение стажа работы по формуле средней арифметической взвешенной

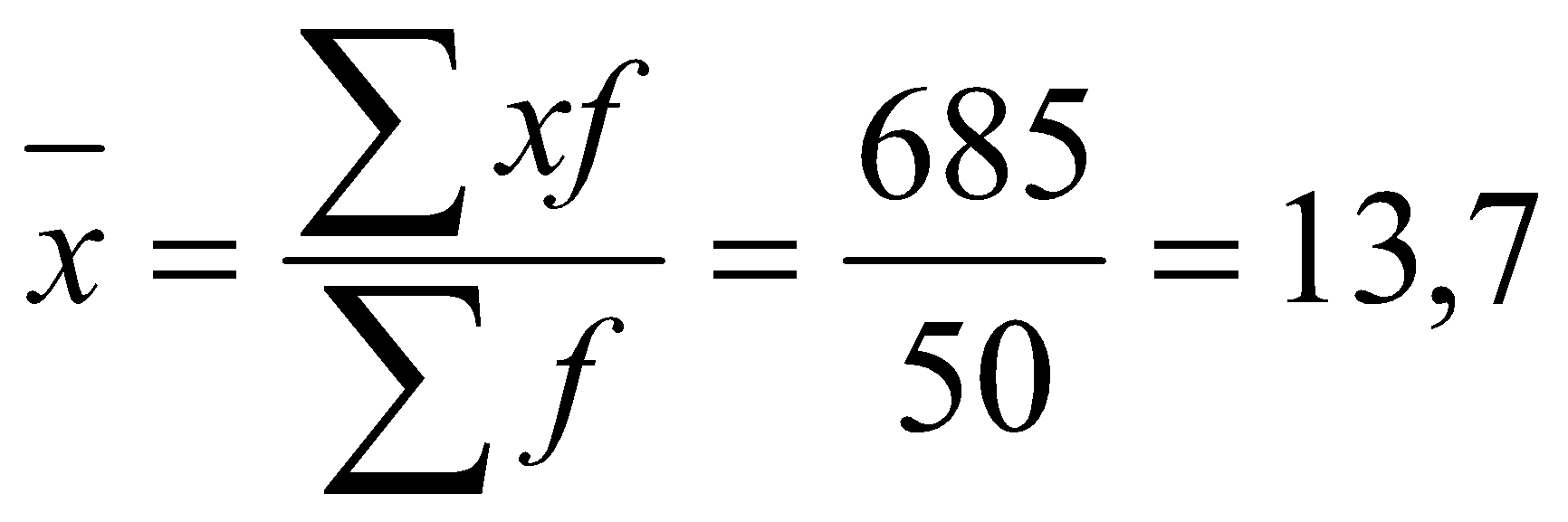лет

2. Рассчитаем дисперсию

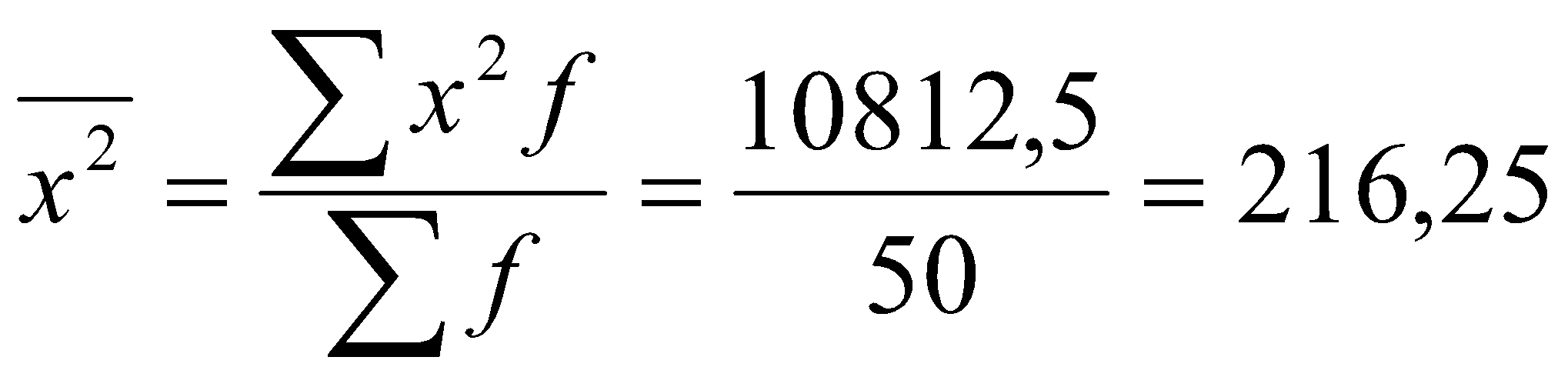
Среднее квадратическое отклонение равно лет

3. Рассчитаем коэффициент вариации:

4. Предельная ошибка для генеральной средней вычисляется по формуле:

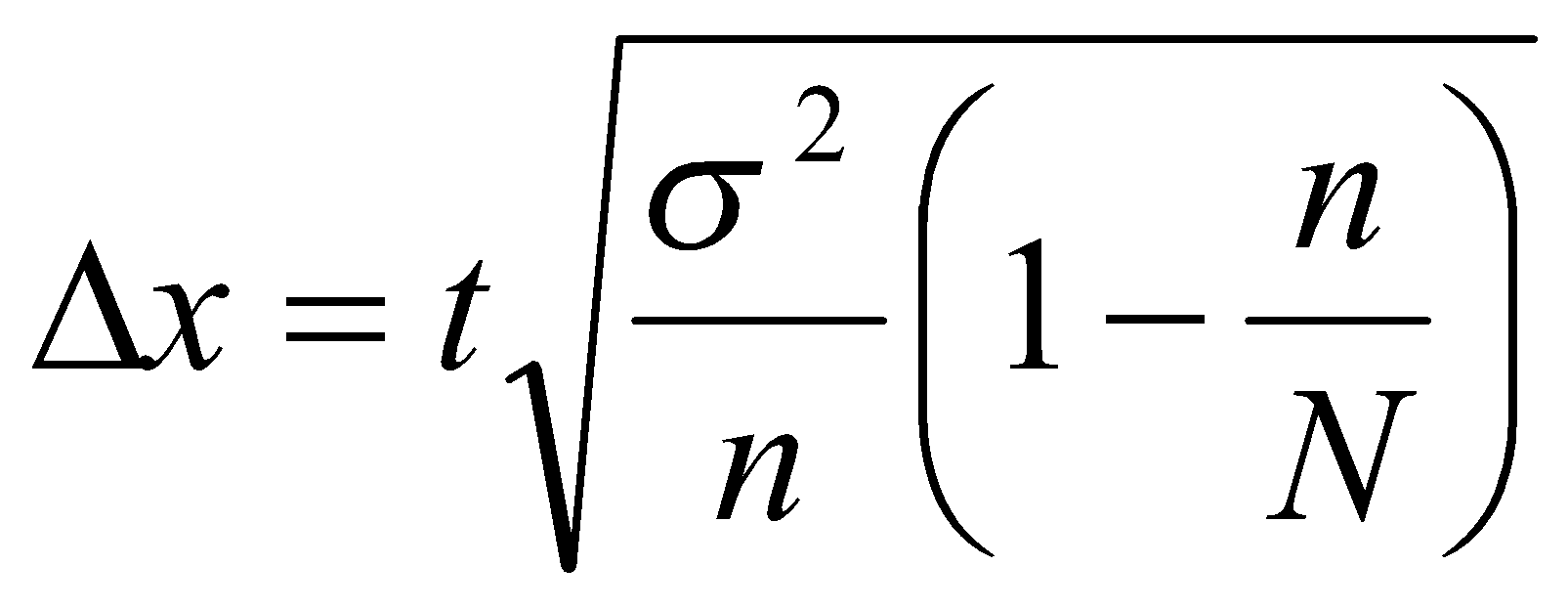, где σ² – дисперсия, n – объем выборки, N – объем генеральной совокупности, а t – коэффициент доверия, зависящий от вероятности, с которой делается утверждение (при P=0,954 t=2).

Т.к. выборка 10%-ная, то отношение . Подставим известные данные в формулу:

Пределы для генеральной средней задаются неравенствами:

Таким образом, интервал, в котором находится средний стаж работы всех работников предприятия, будет

13,7 – 1,436 ≤ ≤ 13,7 + 1,436

12,264 ≤ ≤ 15,136
Выводы: средний стаж работы работников предприятия равен 13,7 лет. Колеблемость стажа от его среднего значения, определяемая коэффициентом вариации, составляет 39%. Т.к. это значение больше 30%, то средний стаж работы нетипичен для данной совокупности. С вероятностью 0,954 можно утверждать, что средний стаж работы всех работников предприятия лежит в пределах от 12,264 до 15,136 лет.

Список литературы

1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1995.
2. Ефимова М.Р. Практикум по общей теории статистики: учебное пособие. – М.: Финансы и статистика, 2003.
3. Практикум по теории статистики: Учебное пособие / Под ред. Р.А. Шмойловой. – М: Финансы и статистика, 1999.
4. Курс социально-экономической статистики: Учебник / Под ред. проф. М.Г. Назарова. – М.: Финстатинформ, ЮНИТИ-ДАНА, 2000.