Как найти среднее значение прибыли

Для вычисления средней прибыли, используйте геометрическое среднее ([a₁·a₂·a₃]^[1/n]), а не арифметическое ([a₁+a₂+a₃]/n).

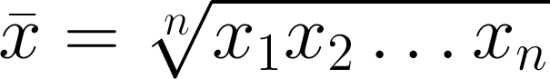
Если прибыль за 3 месяца была 1%, 2,% и 3% соответственно, то средняя месячная прибыль за весь период составляет 2%. Кажется, все правильно. Но это не так!

Для любого человека, связанного с инвестициями, важно знать, с какой скоростью растет прибыль. Будь то трейдеры, брокеры или инвесторы, каждой из групп необходимо каким-то образом измерять среднюю доходность.

Читайте такжеСложные проценты (реинвестирование, капитализация) Сложные проценты начисляют проценты на проценты; ваш вклад растет с невероятной скоростью экспоненты, превращая ваш стартовый капитал в сверхприбыльну…

Т.к. акции, сырье, и другие финансовые инструменты (кроме облигаций, депозитов и других инструментов с фикс. доходностью) не предоставляют никакую гарантию по приросту капитала, доходность их колеблется. Вполне реально получить такую картину доходности в течение 6-ти последовательных месяцев: 15%, 6%, -3%, 36%, 51% и 9%. Но как в таком случае описать прибыльность одним показателем? Какова средняя прибыльность от таких результатов? В этой статье мы порассуждаем про методы вычисления средней прибыли.

Стандартный метод вычисления средней прибыли

Простой метод вычисления средней прибыли использует среднее арифметическое значение. Для показателей доходности из примера выше, среднее арифметическое будет следующим:

(15 + 6 – 3 + 36 + 51 + 9)/6 = 19%

Итого, при стандартном вычислении средней доходности за полгода, средняя месячная доходность в течение периода составила 19%. Давайте проверим, так ли это. Предположим, что мы изначально вложили 100 грн.

1. 100+19%=119
2. 119+19%=141,61
3. 141,61+19% = 168,52
4. 168,52+19% = 200,53
5. 200,53+19% = 238,64
6. 238,64+19% = 283,98 ~ 284 грн.

Т.е., при постоянной доходности в 19% в течение 6 месяцев мы получаем в конце периода 284 грн., при том, что вложили 100. Теперь давайте сравним результат вычислений с реальными доходами помесячно:

1. 100+15% = 115
2. 115+6% = 121,9
3. 121,9-3% = 118,24
4. 118,24+36% = 160,81
5. 160,81+51% = 242,82
6. 242,82+9% = 264,68 ~ 265 грн.

В то время как реальный капитал по завершении периода составил 265 грн., согласно арифметическому методу вычисления средней доходности, капитал составил 284, т.е. почти на 7% больше. Таким образом получается, что стандартный метод вычисления средней прибыли не отражает действительности; это метод преувеличивает реальные показатели от инвестиционной деятельности.

Правильный метод вычисления средней доходности

Читайте такжеЧто такое бид, аск и спред (bid, ask, spread) «Бид» — цена, которую готов заплатить покупатель финансового инструмента. «Аск» — цена, по которой продавец готов продать. «Спред» — разница между цен…

Для того, чтоб правильно вычислить среднюю прибыль за период, необходимо использовать геометрическое среднее значение (оно же — среднее пропорциональное). При вышеупомянутых данных о месячных доходах, средняя месячная прибыль при правильном вычислении будет равна:

(1,15*1,06*0,97*1,36*1,51*1,09)^(1/6) = 17,6124%

Т.е. на самом деле, средняя месячная доходность за период составила 17,61%, что существенно меньше показателей при стандартном просчете, если номиналы измеряются в сотнях тысяч. Давайте проверим правильность этого метода:

1. 100+17,6124% = 117,61
2. 117,61+17,6124% = 138,33
3. 138,33+17,6124% = 162,69
4. 162,69+17,6124% = 191,34
5. 191,34+17,6124% = 225,04
6. 225,04+17,6124% = 264,68

Как видите, этот метод вычисления средней доходности привел в точности к реальному номинальному значению.

Практическое применение знаний

Теперь, когда вы знаете о правильном методе вычисления средней прибыльности, задайте себе и/или менеджеру ваших активов следующие вопросы:

1. какова средняя месячная прибыльность за последний год?
2. каким способом вы вычисляете среднюю доходность?

Имейте ввиду, что завышенную среднюю доходность за период могут использовать все, кому это выгодно и где это уместно: от заманчивой рекламы ПИФов, до вашего персонального брокера. Естественно, относительная разница между средней доходностью просчитанной с помощью арифметического и геометрического средних невелика, но если речь идет о миллионах, то эта «небольшая» разница имеет большое значение.

Вывод

Читайте такжеАналитика рынка ≠ обзор рынка Аналитика рынка — прогноз, вывод, напутствие к действию, а обзор или сводка — это описание текущей ситуации.
Однажды, завязав дискуссию с завистливым…

Умейте правильно оценить вашу среднюю доходность за период. Используйте геометрическое (пропорциональное) среднее, а не арифметическое. Если вам кто-то говорит о показателях средней доходности, спросите, каким способом вычислялась эта средняя доходность и не давайте себя обмануть.

Россия напала на Украину. Это не спец-операция, а настоящая война. Гибнут мирные жители и дети. Не сидите молча. Российские СМИ врут. Если бездействовать то русское общество скоро будет вообще без прав и свобод.

← Понравилась статья? Лайкни и поделись с друзьями.

Россия напала на Украину. Это не спец-операция, а настоящая война. Гибнут мирные жители и дети. Не сидите молча. Российские СМИ врут. Если бездействовать то русское общество скоро будет вообще без прав и свобод.

Федеральное агентство по образованию

Государственное образовательное
учреждение

высшего профессионального образования

«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
УПРАВЛЕНИЯ»

Домашняя работа

по
дисциплине

“Статистика”

Выполнила студентка Просенкова
Наталья

очной формы обучения

специальности

Мировая экономика

курса 2 группы 2

Преподаватель:

Агеева Наталья Константиновна

Москва 2008

№	№ предприятия	Cреднее значение стоимости активов банков за квартал (Xi), млн. руб.	Прибыль банков за квартал (Yi), млн. руб.
1	1	625,04	16,01
2	2	629,27	15,87
3	3	630,88	16,12
4	4	640,99	17,60
5	5	663,36	17,79
6	6	663,83	17,69
7	7	671,75	17,02
8	9	677,16	16,99
9	10	698,74	19,07
10	11	710,84	18,31
11	12	728,57	18,66
12	14	742,17	18,64
13	15	742,33	18,86
14	16	755,13	19,76
15	19	771,05	19,06
16	20	774,81	19,91
17	21	775,49	19,80
18	22	783,05	20,08
19	25	817,76	20,33
20	26	820,35	21,86
21	27	828,00	21,42
22	28	831,67	21,61
23	29	836,73	21,49
24	33	859,75	21,35
25	34	860,83	21,87
26	35	870,58	21,53
27	37	881,16	22,83
28	38	888,17	23,23
29	39	904,58	22,74
30	40	906,13	22,78

Проверим
однородность совокупности по величине
факторного признака (X_i),
подсчитав коэффициент вариации.

=

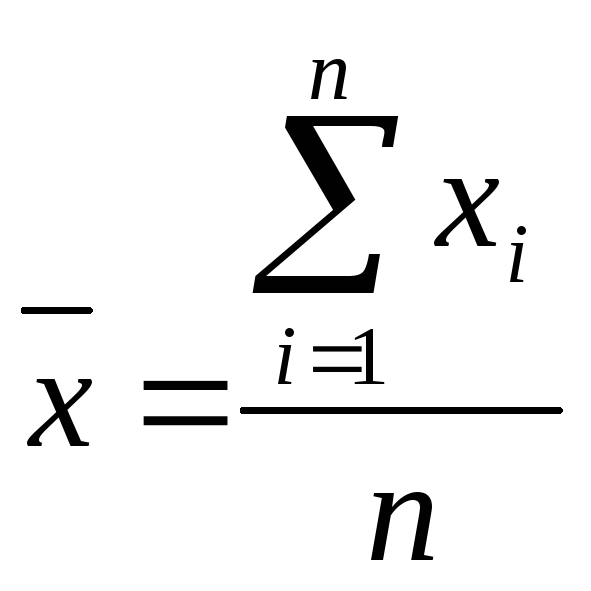
≈ 766,439

=

=

=
%

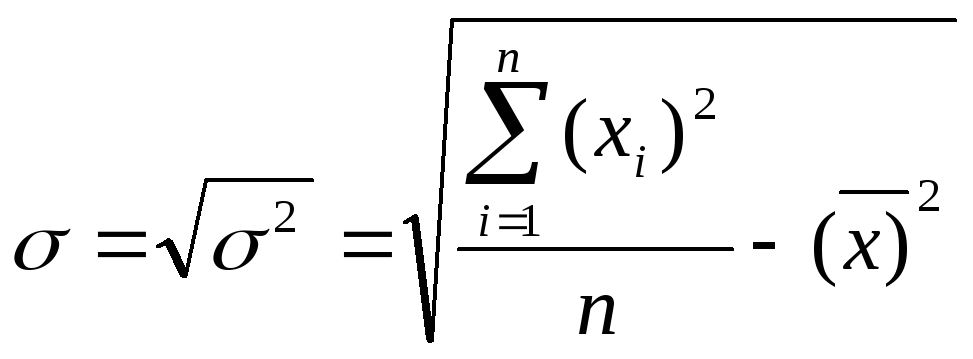
Вывод:
коэффициент вариации <33%, следовательно,
совокупность качественно однородна.

2. Произвести
группировку компаний по стоимости
активов с целью выявления зависимости
между размером компании по стоимости
активов и прибыли. Результаты представить
в виде статистической таблицы,
сформулировать выводы.

Чтобы произвести группировку,
воспользуемся формулой Стерджесса,
приняв m
равным 5:

=

Группы банков по размеру стоимости активов, млн.руб.	Число банков	Стоимость активов в группе, млн.руб.	Прибыль в группе, млн.руб.	Средняя прибыль по группе, млн.руб.	Относит. величина наглядности, %
625,04 – 681,26	8	5202,28	135,09	16,89	75,64
681,26 – 737,48	3	2138,15	56,04	18,68	83,65
737,48 – 793,7	7	5344,03	136,11	19,44	87,06
793,7 – 849,92	5	4134,51	106,71	21,34	95,57
849,92 – 906,14	7	6171,2	156,33	22,33	100
Итого	30	22990,17	590,28	–	–

Вывод:
с увеличением стоимости активов компании
прибыль увеличивается.

3. Построить
ряд распределения компаний по прибыли,
рассчитав величину интервала по формуле
Стерджесса. Для построенного ряда
определить среднюю прибыль, модальное
и медианное значение прибыли, а также
показатели вариации и формы распределения.
Сформулировать выводы.

Количество групп: m = 1 +
3,322lg(n)
=1+3,322 lg(30)=1+3,322*1,477= 5,906 ≈ 6

1)
Рассчитаем величину интервала по формуле
Стерджесса:

=

1,13
≈ 1,5

2) Построим ряд
распределения:

Группы банков по прибыли за квартал, x	Число банков, f	Накопленная частота
15 – 16,5	3	3
16,5 – 18	5	8
18 – 19,5	6	14
19,5 – 21	5	19
21 – 22,5	8	27
22,5 – 24	3	30
итого	30	–

3)
Средняя величина прибыли

=

4)
Мода:

Мода
лежит в интервале (21 – 22,5), так как на
него падает наибольшая частота 8.

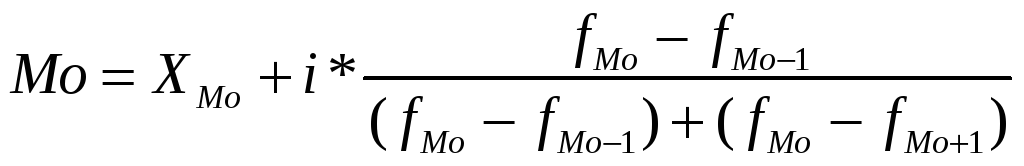=21+1,5*
=

= 21 +
1,5*0,375 = 21,56

Вывод:
наиболее часто встречающееся значение
прибыли предприятия составляет 21,56 млн.
руб.

5)
Медиана:

Найдем
интервал, в котором лежим медиана:

=
15, 5 – следовательно, медиана лежит в
интервале (19,5 – 21)

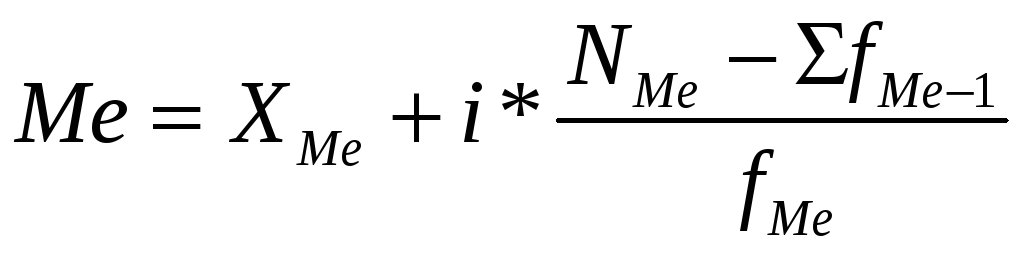
= 19,5 + 1,5*=
19,95

Вывод:
19,95 млн. руб. – это значение прибыли
банков за квартал, которое лежит в
середине ранжированного ряда и делит
его на 2 равные части.

6)
Показатели вариации.

Абсолютные:

1. Размах колебаний:

R=
Xmax-Xmin = 23,23
– 15,87 = 7,36

2.
Среднее линейное отклонение:

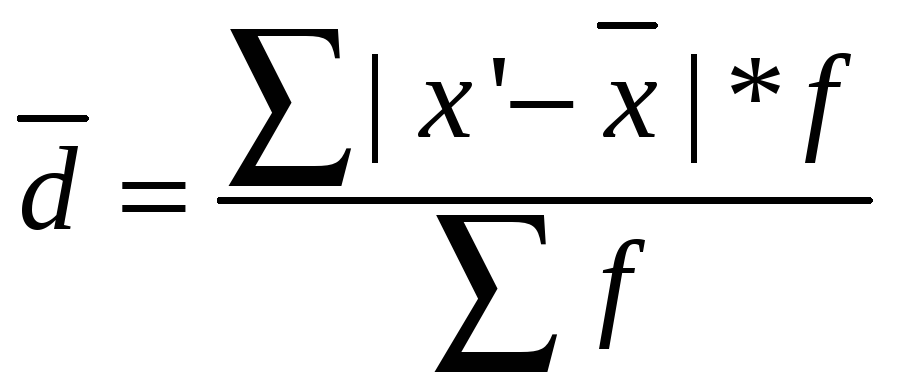
= (|15,75–19,7|*3 + |17,25–19,7|*5 + |18,75–19,7|*6 +
|20,25–19,7|*5 +

+
|21,75–19,7|*8 + |23,25–19,7|*3)/30 = (11,85 + 12,25 + 5,7 + 2,75
+ 16,4 + 10,65)/30 = 1,986

3.
Среднее квадратичное отклонение:

2,278

=
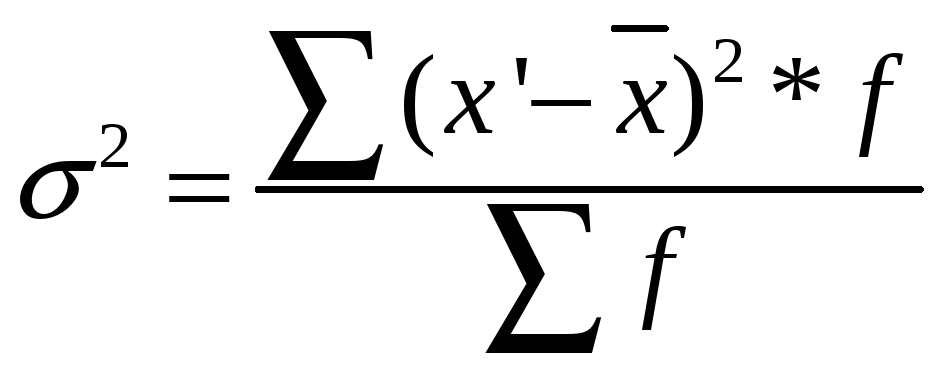(15,84*3 + 6*5 + 0,9*6 + 0,3*5 + 4,20*8 + 12,6*3)/30 = 5,19

Относительные:

1.
Относительный размах колебаний

=
%

2.
Относительное линейное отклонение

=

3.
Коэффициент вариации

=

7)
Показатели формы распределения:

1.
Показатель асимметрии

=

Вывод:
величина показателя асимметрии
положительна, следовательно, асимметрия
правосторонняя. Так как её значение по
модулю >0,25 , то асимметрия значительная.

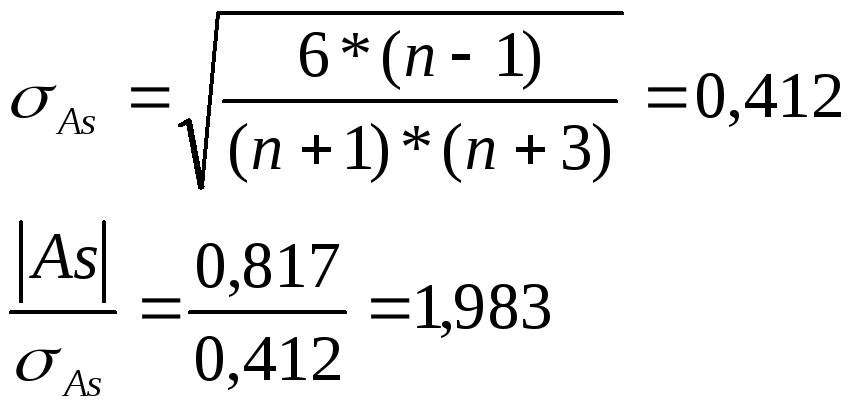
2.
Показатель эксцесса

Ex=

51,117

Ex
=

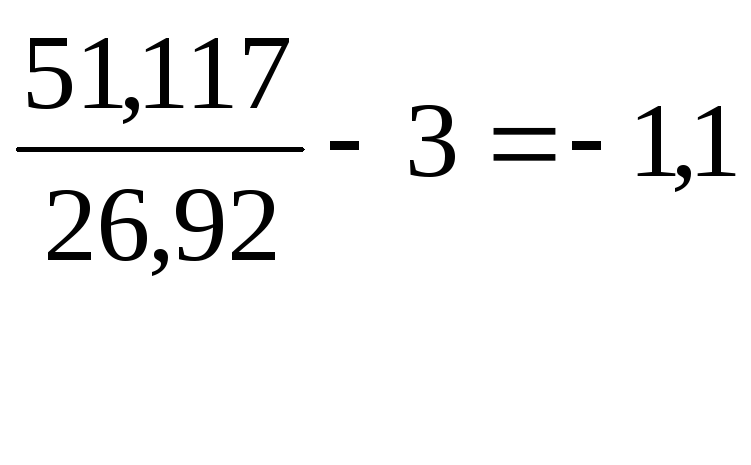
распределение туповершинно

– эксцесс не существенен, значит
распределение нормально.

4. Используя
ранее выполненную группировку
компаний по стоимости активов (пункт
2), проверить правило сложения дисперсий
по объему прибыли.

Группы банков по размеру стоимости активов, млн.руб.	Число банков	Прибыль в группе, млн.руб.	Средняя прибыль по группе, млн.руб.	Относит. величина наглядности, %
625,04 – 681,26	8	135,09	16,89	75,64
681,26 – 737,48	3	56,04	18,68	83,65
737,48 – 793,7	7	136,11	19,44	87,06
793,7 – 849,92	5	106,71	21,34	95,57
849,92 – 906,14	7	156,33	22,33	100
Итого	30	590,28	–	–

Соседние файлы в предмете Экономическая статистика

• #
• #
• #
• #
• #
• #
• #
• #
• #

Как найти среднюю прибыль

Для человека, связанного с вложениями и инвестициями, важно знать и оценивать динамику прибыли. Необходимо пользоваться таким методом определения средней прибыли, который дает наиболее четкое представление об этом показателе.

Инструкция

Понаблюдайте и проанализируйте картину доходности за последние 6 месяцев. Понятно, что акции, сырье и другие финансовые инструменты не могут гарантировать постоянного прироста капитала. Он может колебаться и быть, к примеру, таким: 17%, 5%, -3%, 37%, 51% и 7%. Исключение составляют облигации, депозиты и инструменты, имеющие фиксированную доходность.

Для описания прибыльности используется показатель средней прибыли, который вычисляется несколькими методами, порой, не всегда точно. Простой или стандартный метод определения средней прибыли предполагает использование расчета среднего арифметического значения. Для показателей доходности приведенного выше примера следует, что среднее арифметическое будет составлять:(17 + 5 – 3 + 37 + 51 + 7)/6 = 19. Т.е., средняя месячная доходность составит 19%. Убедитесь, так ли это на самом деле. Предположите, что вы вложили 100 р. Тогда в соответствии с вышеупомянутой ежемесячной доходностью вы получите сумму, равную примерно 284 р. Иными словами, при средней доходности в 19% в течение 6 месяцев вы получили в конце периода 284 р при вложенных 100 р.

Сравните результаты ваших вычислений с реальной ежемесячной прибылью. Проведя несложные вычисления, вы обнаружите, что реальный капитал на конец периода составил 263,77 р, тогда как, согласно арифметическому методу определения средней доходности, он равен 284 р, т.е. приблизительно на 7,1% больше. Так легко убедиться, что стандартный метод не отражает действительности и дает преувеличенные показатели от вашей инвестиционной деятельности.

Чтобы реально оценить среднюю прибыль за конкретный период, используйте формулу среднего геометрического или пропорционального значения, а не среднего арифметического. Для рассматриваемого примера средняя месячная прибыль в процентах при корректном вычислении будет равна: (1,17*1,05*0,97*1,37*1,51*1,07)^(1/6) = 15,8263%, а не 19%, что ниже показателей при стандартном подсчете. Проверив арифметическими расчетами достоверность этого метода, вы убедитесь, что получили реальное значение, равное 263,77 р.

Используйте на практике полученный опыт. Поинтересуйтесь о методе вычисления средней прибыльности, например, собственных активов. Имейте в виду, что заинтересованные организации (от ПИФ до персональных брокеров) могут воспользоваться ситуацией и предоставить вам неверные сведения, что особенно важно при работе с внушительными объемами денежных средств.

Правильно оценивайте вашу среднюю прибыль за определенный период и обязательно уточняйте способ определения этого показателя, не позволяя себя обманывать.

Меры центральной тенденции.

До сих пор мы обсуждали методы, которые мы можем использовать для организации и представления финансовых данных с целью того, чтобы они были более понятными.

Например, частотное распределение доходности класса активов показывает характер рисков, с которыми инвесторы могут столкнуться в конкретном классе активов. Гистограмма годовой доходности S&P 500 ясно показывает, что большие положительные и отрицательные значения годовой доходности являются обычной ситуацией.

Хотя таблицы частотных распределений и гистограммы предоставляют собой удобный способ обобщить серии наблюдений, эти методы являются лишь первым шагом к описанию финансовых данных.

В этом разделе мы обсудим использование количественных показателей, которые объясняют характеристики данных. Наше внимание сосредоточено на мерах центральной тенденции и других показателях (или параметрах), характеризующих положение данных.

Показатель или мера центральной тенденции (англ. ‘measure of central tendency’) указывает, насколько центрированы финансовые данные.

Меры центральной тенденции, вероятно, используются более широко, чем любые другие статистические показатели, потому что их легко рассчитать и применить. Меры положения (англ. ‘measures of location’) включают в себя не только меры центральной тенденции, но и другие показатели, которые иллюстрируют местоположение или распространение данных в рамках распределения.

Далее мы рассмотрим общепринятые меры центральной тенденции – среднее арифметическое, медиану, моду, взвешенное среднее и среднее геометрическое. Мы также объясняем другие полезные меры положения, включая квартили, квинтили, децили и процентили.

Среднее арифметическое.

Финансовые аналитики и портфельные менеджеры часто хотят получить одно число, которое репрезентативно описывает возможный исход инвестиционного решения. Среднее арифметическое – безусловно, наиболее часто используемая мера середины или центра данных.

Определение среднего арифметического.

Среднее арифметическое (англ. ‘arithmetic mean’) – это сумма наблюдений, деленная на количество наблюдений.

Мы можем вычислить среднее арифметическое как для совокупностей, так и для выборок. Эти показатели известны как среднее по совокупности и выборочное среднее значение соответственно.

Среднее значение для совокупности.

Среднее значение для совокупности (математическое ожидание или среднее по совокупности, от англ. ‘population mean’) – это среднее арифметическое значение, рассчитанное для совокупности.

Если мы можем адекватно определить совокупность, то мы можем рассчитать среднее значение для совокупности как среднее арифметическое всех наблюдений или значений в совокупности.

---

Например, аналитики, изучающие годовой рост продаж крупных оптовых клубов в США за 2013 финансовый год, могут определить интересующую совокупность, включив в нее только три компании: BJ’s Wholesale Club (частная компания с 2011 г.), Costco Wholesale Corporation. и Sam’s Club, входящую в группу Wal-Mart.

Оптовый клуб (англ. ‘wholesale club’) – это формат магазина, предназначенного в основном для оптовых продаж в торговых точках размером со склад для клиентов, которые платят членские взносы. По состоянию на начало 2010-х годов эти три оптовых клуба доминировали в данном сегменте в Соединенных Штатах.

В качестве другого примера можно привести портфельного менеджера, специализирующегося на индексе Nikkei 225. Интересующая его совокупность включает 225 акций из первой секции Токийской фондовой биржи, которые формируют индекс Nikkei.

Формула среднего значения для совокупности.

Среднее по совокупности, ( bf mu), является средним арифметическим значением совокупности.

Для конечной совокупности используется следующая формула среднего значения:

Среднее по совокупности является примером статистического параметра. Среднее значение для совокупности уникально; то есть, данная совокупность имеет только одно среднее значение.

---

Чтобы проиллюстрировать расчеты по приведенной формуле, мы можем найти среднее по совокупности для доли прибыли в выручке американских компаний, управляющих крупными оптовыми клубами за 2012 год.

В течение года прибыль в процентах от выручки для оптовых клубов BJ, Costco Wholesale Corporation, и Wal-Mart Stores составляли 0,9%, 1,6% и 3,5% соответственно, согласно списку Fortune 500 за 2012 год. Таким образом, среднее значение по совокупности для прибыли в процентах от выручки составило:

(mu) = (0,9 + 1,6 + 3,5)/3 = 6/3 = 2%

Выборочное среднее значение.

Среднее значение по выборке (выборочное среднее или выборочное среднее значение, от англ. ‘sample mean’) – это среднее арифметическое значение, вычисленное для выборки.

Очень часто мы не можем наблюдать каждый элемент множества данных; вместо этого мы наблюдаем подмножество или выборку из генеральной совокупности.

Концепция среднего значения может применяться к наблюдениям в выборке с небольшим изменением обозначений.

Формула выборочного среднего значения.

Выборочное среднее, ( overline{X} ) (читается как «X-bar») – это среднее арифметическое значение по выборке:

Формула 3 предписывает суммировать значения наблюдений (X_i) и делить эту сумму на количество наблюдений. Например, если выборка коэффициентов прибыли на акцию (P/E) для шести публичных компаний содержит значения 35, 30, 22, 18, 15 и 12, то среднее значение P/E для выборки будет 132/6 = 22. Среднее значение выборки также называется средним арифметическим (англ. ‘arithmetic average’).

Статистики предпочитают использовать термин «mean», а на «average» (в русском переводе это одно и то же – «среднее»). Некоторые авторы называют все меры центральной тенденции (включая медиану и моду) термином «average». Термин «mean» позволяет избежать любой путаницы.

Как отмечалось ранее, выборочное среднее значение является статистикой (то есть описательной мерой выборки).

---

Средние значения можно рассчитывать для отдельных статистических единиц или для временного отрезка.

В качестве примера можно привести рентабельность собственного капитала (ROE) за 2013 год для 100 компаний из FTSE Eurotop 100, индексе 100 крупнейших компаний Европы. В этом случае мы рассчитываем среднее значение ROE за 2013 год в среднем по 100 отдельным статистическим единицам (или элементам множества, от англ. ‘statistical unit’ или просто ‘unit’).

Когда мы изучаем характеристики некоторых статистических единиц в определенный момент времени (например, ROE для FTSE Eurotop 100), мы изучаем перекрестные данные (англ. ‘cross-sectional data’). Среднее этих наблюдений называется перекрестным средним значением (англ. ‘cross-sectional mean’).

[см. также: CFA – Временные ряды и перекрестные данные]

С другой стороны, если наша выборка состоит из исторической месячной доходности по FTSE Eurotop 100 за последние 5 лет, то мы имеем дело с данными временного ряда (англ. ‘time-series data’). Среднее значение этих наблюдений называется средним временного ряда (англ. ‘time-series mean’).

Мы рассмотрим специализированные статистические методы, связанные с поведением временных рядов в следующих разделах, посвященных анализу временных рядов.

Ниже мы покажем пример определения выборочной средней доходности для 16 европейских фондовых рынков за 2012 г. В этом случае среднее значение является перекрестным, поскольку мы усредняем доходность по отдельным странам.

Пример вычисления перекрестного среднего значения.

Индекс MSCI EAFE (Европа, Австралия и Дальний Восток) – это индекс рыночной капитализации, скорректированный с учетом свободного обращения акций, предназначенный для оценки акций в развитых странах, за исключением США и Канады.

Термин «скорректированный с учетом свободного обращения акций» (англ. ‘free float-adjusted’) означает, что веса компаний в индексе отражают стоимость акций, фактически доступных для инвестиций.

По состоянию на сентябрь 2013 года EAFE состояла из 22 индексов стран развитых рынков, включая индексы для 16 европейских рынков, 2 австралийских рынков (Австралия и Новая Зеландия), 3 дальневосточных рынков (Гонконг, Япония и Сингапур) и Израиля.

Предположим, что мы заинтересованы в показателях динамики местной валюты на 16 европейских рынках EAFE в 2012 году. Мы хотим найти примерную среднюю общую доходность за 2012 год по этим 16 рынкам.

Ряды ставок доходности, представленные в Таблице 8, приведены в местной валюте (то есть доходность указана для инвесторов, проживающих в стране). Поскольку эта доходность не указывается в валюте каждого отдельного инвестора, она не является доходностью, которую мог бы получить отдельный инвестор. Это, скорее, средняя доходность для местных валют 16 стран.

Таблица 8. Общая доходность европейских фондовых рынков, 2012 г.

Рынок	Общая доходность в местной валюте (%)
Австрия	20.72
Бельгия	33.99
Дания	28.09
Финляндия	8.27
Франция	15.90
Германия	25.24
Греция	-2.35
Ирландия	2.24
Италия	6.93
Нидерланды	15.36
Норвегия	6.05
Португалия	-2.22
Испания	-4.76
Швеция	12.66
Швейцария	14.83
Великобритания	5.93

Источник: www.msci.com.

Используя данные Таблицы 8, рассчитайте выборочную среднюю доходность для 16 фондовых рынков за 2012 год.

---

Решение:

При расчете к ставкам доходности применяется Формула 3:

(20,72 + 33,99 + 28,09 + 8,27 + 15,90 + 25,24 – 2,35 + 2,24 + 6,93 + 15,36 + 6,05 – 2,22 – 4,76 + 12,66 + 14,83 + 5,93) / 16 = 186,88 / 16 = 11,68%

Мы можем убедиться, что на 8 рынках доходность была меньше среднего, а на других 8 – выше среднего. Мы не должны ожидать, что какие-либо фактические наблюдения будут равны среднему значению, потому что выборочные средние значения предоставляют только сводку анализируемых данных.

Кроме того, хотя в этом примере число значений ниже среднего равно количеству значений выше среднего, это не обязательно так на самом деле. Как финансовому аналитику, вам часто нужно будет находить несколько показателей, которые описывают характеристики распределения.

Среднее значение – это, как правило, статистика, которую вы будете использовать как показатель типичного результата для распределения. Затем вы можете использовать среднее значение для сравнения динамики двух разных рынков.

Например, вам может быть интересно сравнить показатели фондового рынка стран Азиатско-Тихоокеанского региона с показателями фондового рынка европейских стран. Вы можете использовать среднюю доходность этих рынков, чтобы сравнить результаты инвестиций.

Свойства среднего арифметического.

Среднее арифметическое можно сравнить с центром тяжести объекта. Рисунок 5 выражает эту аналогию графически и представляет собой график девять гипотетических наблюдений.

Девять наблюдений: 2, 4, 4, 6, 10, 10, 12, 12 и 12. Среднее арифметическое составляет 72/9 = 8. Наблюдения наносятся на ось как столбцы с различной высотой в зависимости от их частоты (то есть 2 – высота в одну единицу, 4 – высота в две единицы и т. д.).

Когда ось помещается на точку опоры, она сбалансируется только тогда, когда точка опоры совпадает с отметкой на оси, соответствующей среднему арифметическому значению.

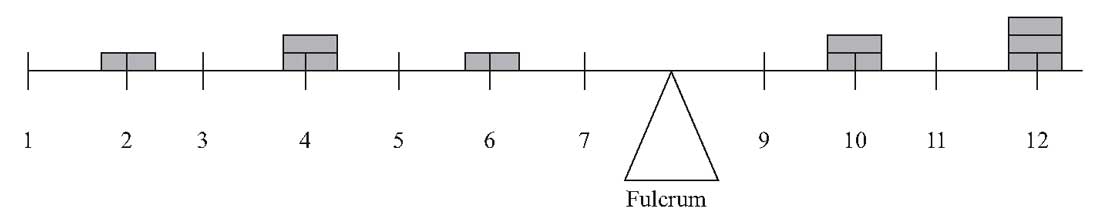Рисунок 5. Аналогия с центром тяжести для среднего арифметического.

Когда точка опоры установлена на отметку 8, ось идеально сбалансирована.

---

Как финансовые аналитики, мы часто используем среднюю доходность как меру типичного результата для актива. Однако, как и в приведенном выше примере, некоторые результаты оказываются выше среднего, а некоторые – ниже. Мы можем рассчитать расстояние между средним значением и каждым результатом и назвать его отклонением (англ. ‘deviation’).

Математически всегда верно, что сумма отклонений от среднего равна 0. Мы можем убедиться в этом, взяв среднее арифметическое, приведенное в Формуле 3, и умножив обе части уравнения на (n):

({ noverline{X} = dsum_{i=1}^{n}X_i })

Таким образом, сумма отклонений от среднего значения может быть рассчитана следующим образом:

({ begin{align} & sum_{i=1}^{n} (X_i – overline{X}) = \ & sum_{i=1}^{n}X_i – sum_{i=1}^{n} overline{X} = \ & sum_{i=1}^{n}X_i – noverline{X} = 0 end{align} })

Отклонения от среднего арифметического являются важной информацией, поскольку они указывают на риск. Концепция отклонений от среднего значения формирует основу для более сложных понятий дисперсии, асимметрии и эксцесса, которые мы обсудим в следующих разделах.

Преимущества и недостатки среднего арифметического.

Преимущество среднего арифметического над двумя другими мерами центральной тенденции, – медианой и модой, состоит в том, что среднее использует всю информацию о размере и величине наблюдений. Со средним арифметическим также легко работать математически.

Потенциальный недостаток среднего арифметического – это его чувствительность к экстремальным значениям.

Поскольку для вычисления среднего значения используются все наблюдения, среднее арифметическое может резко увеличиваться или уменьшаться за счет чрезвычайно больших или малых наблюдений, соответственно.

Например, предположим, что мы вычисляем среднее арифметическое следующих семи чисел: 1, 2, 3, 4, 5, 6 и 1000.

Среднее значение равно 1,021 / 7 = 145,86 или приблизительно 146. Поскольку величина среднего, 146, намного больше, чем величина большинства наблюдений (первые 6), мы можем задаться вопросом, насколько хорошо она представляет положение данных в распределении.

На практике, хотя экстремальное значение (или выброс, от англ. ‘outlier’) в финансовых данных может быть редким значением в совокупности, оно также может отражать ошибку, допущенную при записи значения наблюдения или ошибку при формировании выборки из совокупности.

В частности, в последних двух случаях среднее арифметическое может вводить в заблуждение. Наиболее распространенный подход в таких случаях – использовать медиану вместо или в дополнение к среднему значению.

Медиана будет рассмотрена далее.

---

Другие подходы к обработке экстремальных значений включают применение вариаций среднего арифметического.

Усеченное среднее значение (от англ. ‘trimmed mean’ или ‘truncated mean’) вычисляется путем исключения указанного небольшого процента самых низких и самых высоких значений. Затем вычисляется среднее арифметическое из оставшихся значений.

Например, среднее значение, усеченное на 5%, отбрасывает наименьшие 2,5% и наибольшие 2,5% значений и вычисляет среднее из оставшихся 95% значений.

Усеченное среднее значение часто используется в спортивных соревнованиях, когда самые низкие и самые высокие оценки судей отбрасываются при подсчете оценки участника.

Средняя расчетная прибыль

07 марта 2016 18:43

Средняя расчетная прибыль – показатель, отражающий норму прибыли на инвестиции в течение определенного периода.

Как определяется средняя расчетная прибыль?

Есть несколько факторов, которые должны учитываться при определении средней расчетной прибыли, чтобы этот показатель оказался полезным сразу с нескольких точек зрения.

1. Прежде всего в процессе вычисления средней расчетной прибыли необходимо учитывать расходы, связанные с инвестициями.

1. После того как балансовая стоимость и амортизация оказываются учтенными, следующий необходимый фактор – общий доход, который принес актив за рассматриваемый период времени. Обязательно следует вычесть все налоги, которые предприниматель выплачивает с дохода. Учет общего дохода за вычетом налогов позволит инвестору точнее спрогнозировать прибыль, которую он получит в рамках инвестиционной стратегии.

1. После того как при расчете будет учтен доход минус налог, необходимо разделить это значение на среднюю балансовую стоимость, которая была посчитана ранее. Средняя балансовая стоимость может быть скорректирована на величину износа.

Для чего нужно считать среднюю расчетную прибыль?

Есть несколько причин, по которым показатель средней расчетной прибыли может быть полезен для инвестора. Благодаря этому показателю инвестор может понять реальную ценность актива, что позволит ему сделать вывод, стоит ли покупать дополнительные единицы или лучше сократить потери и предпочесть вложения в другие объекты. Однако вычисление средней расчетной прибыли всего за один период не даст инвестору никакой ценной информации – отслеживать этот показатель следует в динамике за 3-4 периода.

Знание величины средней расчетной прибыли будет полезным для инвестора, собирающего продать имеющийся актив. Информация о том, что актив прибылен уже в течение нескольких периодов, используется для стимулирования потенциальных покупателей.