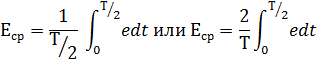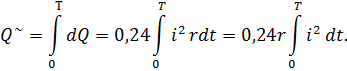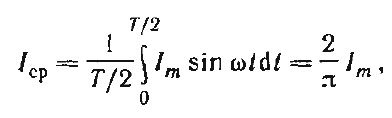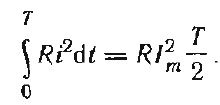Как найти среднее значение силы тока

Среднее
значение переменного напряжения, ЭДС
и тока за период равно нулю, так как
площадь отрицательных и положительных
полуволн синусоид равны по величине и
различны по знаку (рис.2.6).

е,u,i
e

u
i

0t

0

T/2

T

Рис.2.6

Поэтому,
когда говорят о среднем значении
переменного тока i,
напряжения u
или
ЭДС е,

под ним подразумевается среднее значение
за половину периода Т/2 между двумя
нулевыми значениями величины 0 и .

Например,
среднее значение переменной ЭДС любого
вида определяется так:

Если
ЭДС изменяется по синусоидальному
закону е
, то можно установить простую зависимость
между средним значением ЭДС E_ср
и
его амплитудным значением Е_m.

а
так как ,

то
=0,637.

Аналогично
получим средние значения напряжения и
тока:

2.1.4. Действующее значение переменного тока и напряжения.

В
электротехнике часто приходится иметь
дело с тепловыми и механическими
действиями переменного тока.

Механическая
сила взаимодействия двух проводников
с одинаковыми токами и тепловое действие
тока пропорциональны квадрату мгновенных
значений тока. Для переменного тока
тепловое или механическое действие
определяется средним значением квадратов
токов за период, называемым действующим
значением тока.

Иначе
говоря, действующее значение переменного
тока равняется постоянному току,
выделяющему за время, равное периоду,
в каком-либо проводнике такое же
количество тепла, что и данный переменный
ток.

Количество
теплоты, выделяемое постоянным током
в резисторе с активным сопротивлением
r
за промежуток времени Т, равный периоду
переменного тока, составляет:

=0,24

Количество
теплоты, выделяемое переменным током
в том же эелементе за промежуток времени
dt,
равно:

Количество
теплоты, выделяемое за период Т, равно:

Приравнивая
количество теплоты, выделяемое постоянным
и переменным током, получим:

=

Отсюда
получим действующее значение тока:

Аналогично
для напряжений и ЭДС переменного тока
имеем:

Выражения
для I,U
и Е определяют в общем виде действующие
периодические токи, напряжение и ЭДС
при любом законе их изменения.

Для
синусоидального переменного тока i=
будем иметь:

Второй
интеграл равен нулю, и для действующего
синусоидального тока имеем:

Аналогично
получим выражение для действующих
синусоидальных ЭДС и напряжения:

.

Градация
вольтметров и амперметров, предназначенных
для работы в цепи синусоидального тока,
обычно показывает непосредственно
действующие значения напряжения или
тока.

2.1.5.Векторные диаграммы переменного тока.

Как
было установлено, гармонически
изменяющееся напряжение в общем виде
определяется выражением:

Зная
амплитуду напряжения
и аргумент синусоидальной функции ,
можно с помощью несложных математических
операций определить мгновенные значения
напряжения u
в
любой момент времени. Наряду с аналитическим
способом расчета получить u
можно
графически, например, по временной
диаграмме гармонической переменной
(рис.2.7).

Однако
при различных расчетах бывает удобнее
пользоваться методом векторных диаграмм.
Применение векторных диаграмм при
исследовании цепей переменного тока
позволяет наглядно представить
рассматриваемые процессы и упрощать
производимые расчеты.

Y
U

u
Х u

0

u=0

Рис.2.7

Синусоидальный
ток и напряжение можно представить как
вектор, движущийся по окружности со
скоростью
Мгновенные значения будут равны проекции
этого вектора на ось Y.

Суть
данного метода заключается в следующем:
если какая-нибудь точка движется с
постоянной скоростью по окружности, то
её проекция на любой диаметр (горизонтальный-
воображаемая ось Х или вертикальная-
ось Y)
совершает гармонические(синусоидальные
колебания). Радиус-вектор ( в дальнейшем
для краткости будем называть просто
вектор) этой точки вращается с постоянной
угловой скоростью

Y
U_m

U

X
0

U_m

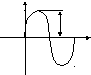
Рис.2.8

Если
этот вектор (рис.2.8) в известном, произвольно
выбранном масштабе изображающий
амплитуду напряжения (
тока и ЭДС), занимает в начальный момент
времени (t=0)
горизонтальное положение, вправо от
центра вращения 0 и вращается против
часовой стрелки с угловой скоростью
,
то в произвольный момент времени t,
когда он образует с горизонталью угол
,
проекция его на вертикальную ось Y
в том же масштабе покажет соответствующее
мгновенное напряжение:

Если
же вектор
в начальный момент расположен не
горизонтально, а образует с осью абсцисс
Х угол ,
то проекция на ось Y
покажет мгновенное значение напряжения
опережающее
предыдущее на часть периода .
Представим этот случай графически.
Расположим под углом
относительно положительной оси абсцисс
вектора ,длина
которого в заранее выбранном масштабе
равна амплитуде изображаемой гармонической
величины (рис.2.9).

Y

U

0 X

Рис.2.9

Положительные
углы ( начальные фазы напряжения ,
а так же только принято
откладывать в направлении против часовой
стрелки, а отрицательные( )-по
часовой стрелке ( рис.2.9, показана
положительная начальная фаза напряжения
).

Предположим,
что вектор
, начиная с момента времени t=0,
вращается вокруг начала координат
против часовой стрелки с постоянной
частотой вращения ,
равной угловой частоте изображаемого
напряжения.

В
момент времени t
вектор
повернется на угол
и будет расположен под углом
по отношению к оси абсцисс X.

Проекция
этого вектора на ось координат Y
в выбранном масштабе равна мгновенному
значению изображаемого напряжения .

Следовательно,
величину, изменяющуюся гармонически
во времени, можно изображать вращающимся
вектором. При начальной фазе, равной
нулю (
когда ,
вектор
для t=0.
(рис.2.8) расположен на оси абсцисс.

При

больше или меньше 0 положение вектора

для t=0
определяется знаком и величиной начальной
фазы напряжения.

Обычно
при расчете цепи используются действующие
ЭДС, напряжения и токи( или амплитуды
этих величин), а так же их сдвиг по фазе
относительно друг друга. Поэтому
рассматриваются неподвижные векторы
для некоторого момента времени, который
выбирается так, чтобы диаграмма была
наглядней. Такая диаграмма называется
векторной. Иными словами векторная
диаграмма является совокупностью
векторов, изображающих движущие
синусоидальные ЭДС, напряжение и токи
или их амплитудные значения. Углы сдвига
по фазе
откладываются в направлении вращении
векторов (против часовой стрелки), если
они положительны (например, ,
и в обратном направлении, если они
отрицательны (.
Если, например, начальный фазовый угол
ЭДС
больше начального фазового угла
(см.временную диаграмму на рис.2.10), то
соответственно сдвиг по фазе
и этот угол откладывается в положительном
направлении от вектора тока (рис.2.10).

Мгновенные
значения ЭДС и тока в начальный момент
отсчета
( для
определяются проекциями амплитудных
значений их векторов
на ось ординат Y
в заданном масштабе расчетных параметров
e
и i.

Рассмотрим
сложение ЭДС, токов и напряжений на
векторной диаграмме. При исследовании
цепи переменного тока часто приходится
складывать ЭДС, токи и напряжения одной
и той же частоты.

Y

e₀ E_m
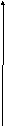
e,i

e i

I_m X

0

Рис.2.10

Предположим,
что требуется сложить две ЭДС:

Такое
сложение можно осуществить аналитически
( путем математических вычислений) и
графически с помощью векторных диаграмм.
Последний способ более нагляден и прост.
Две складываемые ЭДС е₁
и е₂
в определенном масштабе представлены
векторами
и

Y
e e₁

e₂

e
E_m

e₁
E₁

E_2m Ψ_2e E_1m

E_2m

e₂

Ψ_e

Ψ_1e

0
Ψ_1e
Ψ_e
Ψ_2e

Рис.2.11

При
вращении этих векторов с одинаковой
частотой вращения, равной угловой
частоте переменного тока ,
взаимное расположение вращающихся
векторов относительно друг друга
остается неизменным. Сумма проекций
вращающихся векторов
и
на ось ординат (е₁
и е₂)
равна проекции на ту же ось Y
вектора ,
равного геометрической сумме векторов

и :

.

Указанный
способ сложения двух ЭДС универсален,
его можно применить для сложения и
вычитания любого числа ЭДС, напряжений
и токов одной частоты. При этом операцию
вычитания можно представить в виде
сложения, проведя элементарные
преобразования.

Например,
,
то есть уменьшаемая величина складывается
с вычитаемой, взятой с обратным знаком.

На
практике векторные диаграммы, как
правило, строятся не для амплитудных
значений переменных ЭДС, напряжений и
токов, а для действующих величие E,U
и I,
пропорциональных амплитудных значениям
так
как все расчеты цепей выполняются для
действующих значений ЭДС, напряжений
и токов.

Среднее значение

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода.

Среднее значение тока:

т. е. среднее значение синусоидального тока составляет 2/π = 0,638 от амплитудного. Аналогично, Eср = 2Ем/π ; Ucp = 2Uм/π.

Действующее значение

Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным).

Действующее значение тока:

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично 

Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.

Количество теплоты, выделенное за один период синусоидальным током,

Выделенная за то же время постоянным током теплота равна RI^2_пост Т. Приравняем их:

Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

Большинство измерительных приборов показывает действующее значение измеряемой величины.

Действующее значение переменного тока. Характеристики переменного тока

К основным характеристикам переменного тока относятся:

1. Амплитуда, являющаяся максимальным значением периодически изменяющегося тока.
2. Период, который является временем, в течении которого электрическим током совершается полный цикл изменений, после чего они повторяются в той же последовательности.
3. Частота, которая обратна периоду, то есть показывает количество завершенных циклов изменений за единицу времени.
4. Мгновенное значение, являющееся значением переменного тока в конкретный момент времени.
5. Угловая скорость или угловая частота, которая характеризуется углом поворота рамки за единицу времени.

В современной литературе обычно используется математическое определение действующего значения переменного тока, которое звучит следующим образом: действующее значение переменного тока – среднеквадратичное значение переменного тока. Таким образом эта величина рассчитывается по следующей формуле:

Существует пять типичных случаев переменного электрического тока:

1. Синусоида.
2. Прямоугольная форма.
3. Треугольная форма.
4. Трапециевидная форма.
5. Дугообразная форма.

Для синусоидального тока формула для расчета действующего значения выглядит следующим образом:

«Действующее и среднее значение переменного тока» 👇

где Im – амплитудное значение тока.

Для электрического тока, который имеет форму однополярного прямоугольного импульса используется следующая формула для расчета действующего значения.

где D – коэффициент заполнения.

Если коэффициент заполнения равен 0,5, то есть ток имеет форму однополярного меандра, то формула выглядит так:

$I = Im* √0.5 = 0.707*Im$

В том случае, когда у тока форма двуxполярного меандра, то:

$I = Im$

Для токов пилообразной и треугольной формы расчет действующего значения осуществляется по формуле:

Посредством разбивки периода на отрезки действия максимального значения, положительного фронта и отрицательного фронта, получается формула для расчета действующего значения переменного тока трапециевидной формы:

где: t1, t2, t3 – соответственно продолжительность положительного фронта, действия максимального значения и отрицательного фронта; Т – длительность полного периода.

Для тока, который имеет форму дуги или половины окружности, формула для расчета действующего значения имеет следующий вид:

Для измерения тока в цепях переменного тока большинство электроизмерительных приборов, таких как вольтметры и амперметры, градуируются таким образом, чтобы показания соответствовали эффективному значению переменного тока или напряжения.

Среднее значение переменного тока. Коэффициенты амплитуды и формы

Среднее значение переменного тока эквивалентно постоянному по величине электричества, которое проходит через поперечное сечение проводника за определенный промежуток времени. если электрический ток изменяется согласно синусоидальному закону, то за пол через поперечное сечение проводника проходит определенное количество электричества и в определенном направлении. Таким образом его среднее значение за один период равно нулю:

$Iс=0$

Поэтому в данном случае среднее значение переменного синусоидального тока определяется за половину периода, и формула выглядит следующим образом:

$Ic = Q / (T/2)$

где: Q – количество электричества; Т – длительность периода.

Рассмотрим рисунок, который представлен ниже.

В общем виде значение переменного тока рассчитывается по формуле:

$i = dQ / dt$

Отсюда получается, что

$Q = idt$

Таким образом среднее значение синусоидального переменного тока за половину период и с начальной фазой равной нулю на представленном выше рисунке рассчитывается по формуле:

Где: w – угловая скорость; $Т = 1/f; w = 2*п*f; п = 3,14; f $- частота электрического тока.

Графически среднее значение синусоидального переменного тока является высотой прямоугольника, основание которого равняется половине периода, а площадь ограниченна кривой электрического тока и осью абсцисс за половину периода.

Средним значением переменной величины является постоянная составляющая данной величины. Поэтому, чтобы рассчитать среднее значение переменного напряжения и электродвижущей силы можно использовать формулы:

$Uc = (2/п )* Um$

$Ec = (2/п)*Em$

где: Um – амплитудное значение напряжения; Еm – амплитудное значение электродвижущей силы.

Отклонения кривых электрического тока от синусоиды характеризуется коэффициентами формы и амплитуды. Отношением действующего значения переменной величины к ее среднему значению определяется коэффициент формы, то есть:

$Кф = I/Ic$

Коэффициент формы должен учитываться в процессе проектирования и изучения выпрямительных устройств и электрических машин. Для синусоиды коэффициент формы рассчитывается следующим образом:

$Кф = (Im*п) / (√2*2*Im) = 1.11$

Чтобы рассчитать коэффициент амплитуды, используется формула:

$Ка = Im / I$

где I – действующее значение переменного тока.

Для синусоидальной величины формула имеет следующий вид:

$Ка = (I*√2) / I = /2 = 1,41$

Чем больше значение коэффициентов амплитуды и формы отличаются от иx значения для синусоидальных величин, тем больше кривая электрического тока отличается от синусоиды.

Решение: элементарное количество теплоты dQ, выделившееся в проводнике за время dt, равно
[ dQ=I^{2} cdot Rcdot dt, ]
Здесь I сила тока. По условию задачи, ток равномерно возрастает, т.е. линейно зависит от времени
[ begin{array}{l} {I=kcdot t+I_{0} =kcdot t,} \ {k=frac{I_{max } +I_{0} }{tau } =frac{I_{max }}{tau }.} end{array} ]
Здесь τ = 10 с, I_max – значение силы тока через время τ, I₀ = 0 – начальное значение силы тока, k – коэффициент пропорциональности. Полное количество теплоты Q найдём интегрированием
[ begin{array}{l} {Q=int dQ=int _{0}^{tau }k^{2} cdot Rcdot t^{2} dt  =k^{2} cdot Rcdot int _{0}^{tau }t^{2} dt =k^{2} cdot Rcdot frac{tau ^{3} }{3},} \ {Q=left(frac{I_{max }}{tau } right)^{2} cdot Rcdot frac{tau ^{3} }{3} =frac{1}{3} cdot I_{max }^{2} cdot Rcdot tau ,} \ {I_{max } =sqrt{frac{3cdot Q}{Rcdot tau }}.} end{array} ]
Среднее значение силы тока в проводнике при равномерном (линейном) изменении тока найдём как среднее арифметическое значение
[ begin{array}{l} {leftlangle Irightrangle =frac{I_{max } +I_{0}}{2} =frac{I_{max }}{2} ,} \ {leftlangle Irightrangle =frac{1}{2} cdot sqrt{frac{3cdot Q}{Rcdot tau }}.} end{array} ]
Ответ: 10,95 А ≈ 11 А.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 апреля 2018 года; проверки требуют 4 правки.

В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

Значения переменного напряжения (тока)[править | править код]

Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.

Мгновенное значение[править | править код]

Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является (      ).
Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.

Амплитудное значение[править | править код]

• Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение[править | править код]

Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями и совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.

В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

Среднее значение[править | править код]

Среднее значение (смещение) — постоянная составляющая напряжения или силы тока

В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения).
Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.

Средневыпрямленное значение[править | править код]

Средневыпрямленное значение — среднее значение модуля сигнала

На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

Коэффициенты пересчёта значений[править | править код]

• Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен .

• Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен .

Параметры постоянного тока[править | править код]

• Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

• Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
  • Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
  • Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Литература и документация[править | править код]

Литература[править | править код]

• Справочник по радиоэлектронным устройствам: В 2-х т.; Под ред. Д. П. Линде — М.: Энергия, 1978 (недоступная ссылка)
• Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989

Нормативно-техническая документация[править | править код]

• ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
• ГОСТ 23875-88 Качество электрической энергии. Термины и определения
• ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения

Ссылки[править | править код]

• Электрические цепи постоянного тока
• Переменный ток. Изображение синусоидальных переменных
• Амплитудное, среднее, эффективное Архивная копия от 11 июня 2008 на Wayback Machine
• Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
• Системы тока и номинальные напряжения электроустановок
• Электричество
• Проблемы высших гармоник в современных системах электропитания

См. также[править | править код]

• Электрическое напряжение
• Сила тока
• Действующее значение переменного тока
• Вольтметр
• Амперметр
• Осциллограф