Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-
1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-
2
Сосчитайте количество чисел. У нас есть три цифры.
-
3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-
1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-
2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-
1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-
2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 352 737 раз.
Была ли эта статья полезной?
Среднее арифметическое, размах, мода и медиана
- Алгебра
- Среднее арифметическое, размах, мода и медиана
Статистические характеристики
количество чисел
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда
чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите
рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих
чисел на число слагаемых.
Для ряда a1,a1,..,an среднее арифметическое вычисляется по
формуле:
begin{align}
& overline{a}=frac{a_1+a_2+…+a_n}{n}\
end{align}
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
begin{align}
& overline{a}=frac{5,24+6,97+8,56+7,32+6,23}{5}=6.864\
end{align}
Размахом ряда чисел называется разность между наибольшим и наименьшим из
этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще
других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется
число, записанное посередине, а медианой упорядоченного ряда чисел с чётным
числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного
ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды
ряда.
-
Среднее арифметическое чисел 30, 5, 23, 5, 28, 30
begin{align}
& overline{a}=frac{30+5+23+5+28+30}{6}=20frac{1}{6}\
end{align}Размах ряда: 30-5=25
Моды ряда: 5 и 30
Медиана ряда: 25.5
-
Среднее арифметическое чисел 40, 35, 30, 25, 30, 35
begin{align}
& overline{a}=frac{40+35+30+25+30+35}{6}=32frac{1}{2}\
end{align}Размах ряда: 40-25=15
Моды ряда: 30, 35
Медиана ряда: 32.5
-
Среднее арифметическое чисел 21, 18,5, 25,3, 18,5, 17,9
begin{align}
& overline{a}=frac{21+18,5+25,3+18,5+17,9}{5}=20,24\
end{align}Размах ряда: 25,3-17,9=7,4
Мода ряда: 18,5
Медиана ряда: 18,5
Примеры
Примеры нахождения среднего арифметического отрицательных и вещественных чисел.
-
Среднее арифметическое чисел 67,1, 68,2, 67,1, 70,4, 68,2
begin{align}
& overline{a}=frac{67,1+68,2+67,1+70,4+68,2}{5}=68,2\
end{align}Размах ряда: 70,4-67,1=3,3
Моды ряда: 67.1, 68.2
Медиана ряда: 68.2
-
Среднее арифметическое чисел 0,6, 0,8, 0,5, 0,9, 1,1
begin{align}
& overline{a}=frac{0,6+0,8+0,5+0,9+1,1}{5}=0.78\
end{align}Размах ряда: 1,1-0,5=0.6
Ряд не имеет моды
Медиана ряда: 0.8
-
Среднее арифметическое чисел -21, -33, -35, -19, -20, -22
begin{align}
& overline{a}=frac{(-21)+(-33)+(-35)+(-19)+(-20)+(-22)}{6}=-25\
end{align}Размах ряда: (-19)-(-35)=16
Ряд не имеет моды
Медиана ряда: -21,5
-
Среднее арифметическое чисел -4, -6, 0, -4, 0, 6, 8, -12
begin{align}
& overline{a}=frac{(-4)+(-6)+0+(-4)+0+6+8+(-12)}{8}=-1,5\
end{align}Размах ряда: 8-(-12)=20
Моды ряда: -4, 0
Медиана ряда: -2
-
Среднее арифметическое чисел 275, 286, 250, 290, 296, 315, 325
begin{align}
& overline{a}=frac{275+286+250+290+296+315+325}{7}=291\
end{align}Размах ряда: 325-250=75
Ряд не имеет моды
Медиана ряда: 290
-
Среднее арифметическое чисел 38, 42, 36, 45, 48, 45, 45, 42, 40, 47, 39
begin{align}
& overline{a}=frac{38+42+36+45+48+45+45+42+40+47+39}{11}=42frac{6}{11}\
end{align}Размах ряда: 48-36=12
Мода ряда: 45
Медиана ряда: 42
-
Среднее арифметическое чисел 3,8, 7,2, 6,4, 6,8, 7,2
begin{align}
& overline{a}=frac{3,8+7,2+6,4+6,8+7,2}{5}=6,28\
end{align}Размах ряда: 7,2-3,8=3,4
Мода ряда: 7,2
Медиана ряда: 6,8
-
Среднее арифметическое чисел 21,6, 37,3, 16,4, 12,6
begin{align}
& overline{a}=frac{21,6+37,3+16,4+12,6}{4}=21,025\
end{align}Размах ряда: 37,3-12,6=24,7
Мода ряда: 12,6
Медиана ряда: 17,1
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.
Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.
Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:
Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.
Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.
Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.
Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.
Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.
Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».
Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.
Меры центральной тенденции.
До сих пор мы обсуждали методы, которые мы можем использовать для организации и представления финансовых данных с целью того, чтобы они были более понятными.
Например, частотное распределение доходности класса активов показывает характер рисков, с которыми инвесторы могут столкнуться в конкретном классе активов. Гистограмма годовой доходности S&P 500 ясно показывает, что большие положительные и отрицательные значения годовой доходности являются обычной ситуацией.
Хотя таблицы частотных распределений и гистограммы предоставляют собой удобный способ обобщить серии наблюдений, эти методы являются лишь первым шагом к описанию финансовых данных.
В этом разделе мы обсудим использование количественных показателей, которые объясняют характеристики данных. Наше внимание сосредоточено на мерах центральной тенденции и других показателях (или параметрах), характеризующих положение данных.
Показатель или мера центральной тенденции (англ. ‘measure of central tendency’) указывает, насколько центрированы финансовые данные.
Меры центральной тенденции, вероятно, используются более широко, чем любые другие статистические показатели, потому что их легко рассчитать и применить. Меры положения (англ. ‘measures of location’) включают в себя не только меры центральной тенденции, но и другие показатели, которые иллюстрируют местоположение или распространение данных в рамках распределения.
Далее мы рассмотрим общепринятые меры центральной тенденции – среднее арифметическое, медиану, моду, взвешенное среднее и среднее геометрическое. Мы также объясняем другие полезные меры положения, включая квартили, квинтили, децили и процентили.
Среднее арифметическое.
Финансовые аналитики и портфельные менеджеры часто хотят получить одно число, которое репрезентативно описывает возможный исход инвестиционного решения. Среднее арифметическое – безусловно, наиболее часто используемая мера середины или центра данных.
Определение среднего арифметического.
Среднее арифметическое (англ. ‘arithmetic mean’) – это сумма наблюдений, деленная на количество наблюдений.
Мы можем вычислить среднее арифметическое как для совокупностей, так и для выборок. Эти показатели известны как среднее по совокупности и выборочное среднее значение соответственно.
Среднее значение для совокупности.
Среднее значение для совокупности (математическое ожидание или среднее по совокупности, от англ. ‘population mean’) – это среднее арифметическое значение, рассчитанное для совокупности.
Если мы можем адекватно определить совокупность, то мы можем рассчитать среднее значение для совокупности как среднее арифметическое всех наблюдений или значений в совокупности.
Например, аналитики, изучающие годовой рост продаж крупных оптовых клубов в США за 2013 финансовый год, могут определить интересующую совокупность, включив в нее только три компании: BJ’s Wholesale Club (частная компания с 2011 г.), Costco Wholesale Corporation. и Sam’s Club, входящую в группу Wal-Mart.
Оптовый клуб (англ. ‘wholesale club’) – это формат магазина, предназначенного в основном для оптовых продаж в торговых точках размером со склад для клиентов, которые платят членские взносы. По состоянию на начало 2010-х годов эти три оптовых клуба доминировали в данном сегменте в Соединенных Штатах.
В качестве другого примера можно привести портфельного менеджера, специализирующегося на индексе Nikkei 225. Интересующая его совокупность включает 225 акций из первой секции Токийской фондовой биржи, которые формируют индекс Nikkei.
Формула среднего значения для совокупности.
Среднее по совокупности, ( bf mu), является средним арифметическим значением совокупности.
Для конечной совокупности используется следующая формула среднего значения:
(large{ mu = {dsum_{i=1}^{N}X_i over N} }) (Формула 2)
где:
- (N) – количество наблюдений во всей совокупности, а
- (X_i) – (i)-е наблюдение.
Среднее по совокупности является примером статистического параметра. Среднее значение для совокупности уникально; то есть, данная совокупность имеет только одно среднее значение.
Чтобы проиллюстрировать расчеты по приведенной формуле, мы можем найти среднее по совокупности для доли прибыли в выручке американских компаний, управляющих крупными оптовыми клубами за 2012 год.
В течение года прибыль в процентах от выручки для оптовых клубов BJ, Costco Wholesale Corporation, и Wal-Mart Stores составляли 0,9%, 1,6% и 3,5% соответственно, согласно списку Fortune 500 за 2012 год. Таким образом, среднее значение по совокупности для прибыли в процентах от выручки составило:
(mu) = (0,9 + 1,6 + 3,5)/3 = 6/3 = 2%
Выборочное среднее значение.
Среднее значение по выборке (выборочное среднее или выборочное среднее значение, от англ. ‘sample mean’) – это среднее арифметическое значение, вычисленное для выборки.
Очень часто мы не можем наблюдать каждый элемент множества данных; вместо этого мы наблюдаем подмножество или выборку из генеральной совокупности.
Концепция среднего значения может применяться к наблюдениям в выборке с небольшим изменением обозначений.
Формула выборочного среднего значения.
Выборочное среднее, ( overline{X} ) (читается как «X-bar») – это среднее арифметическое значение по выборке:
(large{ overline{X} = {dsum_{i=1}^{n}X_i over n} }) (Формула 3)
где:
- (n) – количество наблюдений в выборке.
Формула 3 предписывает суммировать значения наблюдений (X_i) и делить эту сумму на количество наблюдений. Например, если выборка коэффициентов прибыли на акцию (P/E) для шести публичных компаний содержит значения 35, 30, 22, 18, 15 и 12, то среднее значение P/E для выборки будет 132/6 = 22. Среднее значение выборки также называется средним арифметическим (англ. ‘arithmetic average’).
Статистики предпочитают использовать термин «mean», а на «average» (в русском переводе это одно и то же – «среднее»). Некоторые авторы называют все меры центральной тенденции (включая медиану и моду) термином «average». Термин «mean» позволяет избежать любой путаницы.
Как отмечалось ранее, выборочное среднее значение является статистикой (то есть описательной мерой выборки).
Средние значения можно рассчитывать для отдельных статистических единиц или для временного отрезка.
В качестве примера можно привести рентабельность собственного капитала (ROE) за 2013 год для 100 компаний из FTSE Eurotop 100, индексе 100 крупнейших компаний Европы. В этом случае мы рассчитываем среднее значение ROE за 2013 год в среднем по 100 отдельным статистическим единицам (или элементам множества, от англ. ‘statistical unit’ или просто ‘unit’).
Когда мы изучаем характеристики некоторых статистических единиц в определенный момент времени (например, ROE для FTSE Eurotop 100), мы изучаем перекрестные данные (англ. ‘cross-sectional data’). Среднее этих наблюдений называется перекрестным средним значением (англ. ‘cross-sectional mean’).
[см. также: CFA – Временные ряды и перекрестные данные]
С другой стороны, если наша выборка состоит из исторической месячной доходности по FTSE Eurotop 100 за последние 5 лет, то мы имеем дело с данными временного ряда (англ. ‘time-series data’). Среднее значение этих наблюдений называется средним временного ряда (англ. ‘time-series mean’).
Мы рассмотрим специализированные статистические методы, связанные с поведением временных рядов в следующих разделах, посвященных анализу временных рядов.
Ниже мы покажем пример определения выборочной средней доходности для 16 европейских фондовых рынков за 2012 г. В этом случае среднее значение является перекрестным, поскольку мы усредняем доходность по отдельным странам.
Пример вычисления перекрестного среднего значения.
Индекс MSCI EAFE (Европа, Австралия и Дальний Восток) – это индекс рыночной капитализации, скорректированный с учетом свободного обращения акций, предназначенный для оценки акций в развитых странах, за исключением США и Канады.
Термин «скорректированный с учетом свободного обращения акций» (англ. ‘free float-adjusted’) означает, что веса компаний в индексе отражают стоимость акций, фактически доступных для инвестиций.
По состоянию на сентябрь 2013 года EAFE состояла из 22 индексов стран развитых рынков, включая индексы для 16 европейских рынков, 2 австралийских рынков (Австралия и Новая Зеландия), 3 дальневосточных рынков (Гонконг, Япония и Сингапур) и Израиля.
Предположим, что мы заинтересованы в показателях динамики местной валюты на 16 европейских рынках EAFE в 2012 году. Мы хотим найти примерную среднюю общую доходность за 2012 год по этим 16 рынкам.
Ряды ставок доходности, представленные в Таблице 8, приведены в местной валюте (то есть доходность указана для инвесторов, проживающих в стране). Поскольку эта доходность не указывается в валюте каждого отдельного инвестора, она не является доходностью, которую мог бы получить отдельный инвестор. Это, скорее, средняя доходность для местных валют 16 стран.
|
Рынок |
Общая доходность |
|---|---|
|
Австрия |
20.72 |
|
Бельгия |
33.99 |
|
Дания |
28.09 |
|
Финляндия |
8.27 |
|
Франция |
15.90 |
|
Германия |
25.24 |
|
Греция |
-2.35 |
|
Ирландия |
2.24 |
|
Италия |
6.93 |
|
Нидерланды |
15.36 |
|
Норвегия |
6.05 |
|
Португалия |
-2.22 |
|
Испания |
-4.76 |
|
Швеция |
12.66 |
|
Швейцария |
14.83 |
|
Великобритания |
5.93 |
Источник: www.msci.com.
Используя данные Таблицы 8, рассчитайте выборочную среднюю доходность для 16 фондовых рынков за 2012 год.
Решение:
При расчете к ставкам доходности применяется Формула 3:
(20,72 + 33,99 + 28,09 + 8,27 + 15,90 + 25,24 – 2,35 + 2,24 + 6,93 + 15,36 + 6,05 – 2,22 – 4,76 + 12,66 + 14,83 + 5,93) / 16 = 186,88 / 16 = 11,68%
Мы можем убедиться, что на 8 рынках доходность была меньше среднего, а на других 8 – выше среднего. Мы не должны ожидать, что какие-либо фактические наблюдения будут равны среднему значению, потому что выборочные средние значения предоставляют только сводку анализируемых данных.
Кроме того, хотя в этом примере число значений ниже среднего равно количеству значений выше среднего, это не обязательно так на самом деле. Как финансовому аналитику, вам часто нужно будет находить несколько показателей, которые описывают характеристики распределения.
Среднее значение – это, как правило, статистика, которую вы будете использовать как показатель типичного результата для распределения. Затем вы можете использовать среднее значение для сравнения динамики двух разных рынков.
Например, вам может быть интересно сравнить показатели фондового рынка стран Азиатско-Тихоокеанского региона с показателями фондового рынка европейских стран. Вы можете использовать среднюю доходность этих рынков, чтобы сравнить результаты инвестиций.
Свойства среднего арифметического.
Среднее арифметическое можно сравнить с центром тяжести объекта. Рисунок 5 выражает эту аналогию графически и представляет собой график девять гипотетических наблюдений.
Девять наблюдений: 2, 4, 4, 6, 10, 10, 12, 12 и 12. Среднее арифметическое составляет 72/9 = 8. Наблюдения наносятся на ось как столбцы с различной высотой в зависимости от их частоты (то есть 2 – высота в одну единицу, 4 – высота в две единицы и т. д.).
Когда ось помещается на точку опоры, она сбалансируется только тогда, когда точка опоры совпадает с отметкой на оси, соответствующей среднему арифметическому значению.
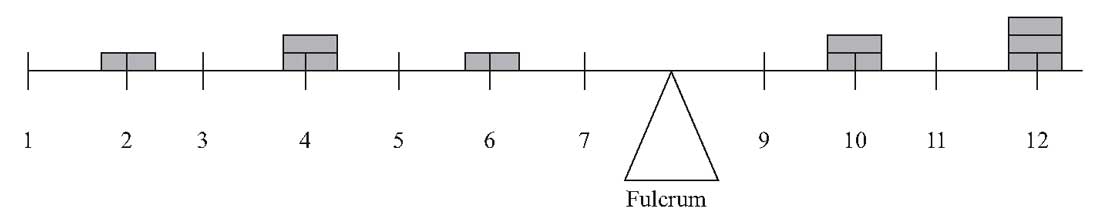
Когда точка опоры установлена на отметку 8, ось идеально сбалансирована.
Как финансовые аналитики, мы часто используем среднюю доходность как меру типичного результата для актива. Однако, как и в приведенном выше примере, некоторые результаты оказываются выше среднего, а некоторые – ниже. Мы можем рассчитать расстояние между средним значением и каждым результатом и назвать его отклонением (англ. ‘deviation’).
Математически всегда верно, что сумма отклонений от среднего равна 0. Мы можем убедиться в этом, взяв среднее арифметическое, приведенное в Формуле 3, и умножив обе части уравнения на (n):
({ noverline{X} = dsum_{i=1}^{n}X_i })
Таким образом, сумма отклонений от среднего значения может быть рассчитана следующим образом:
({ begin{align} & sum_{i=1}^{n} (X_i – overline{X}) = \ & sum_{i=1}^{n}X_i – sum_{i=1}^{n} overline{X} = \ & sum_{i=1}^{n}X_i – noverline{X} = 0 end{align} })
Отклонения от среднего арифметического являются важной информацией, поскольку они указывают на риск. Концепция отклонений от среднего значения формирует основу для более сложных понятий дисперсии, асимметрии и эксцесса, которые мы обсудим в следующих разделах.
Преимущества и недостатки среднего арифметического.
Преимущество среднего арифметического над двумя другими мерами центральной тенденции, – медианой и модой, состоит в том, что среднее использует всю информацию о размере и величине наблюдений. Со средним арифметическим также легко работать математически.
Потенциальный недостаток среднего арифметического – это его чувствительность к экстремальным значениям.
Поскольку для вычисления среднего значения используются все наблюдения, среднее арифметическое может резко увеличиваться или уменьшаться за счет чрезвычайно больших или малых наблюдений, соответственно.
Например, предположим, что мы вычисляем среднее арифметическое следующих семи чисел: 1, 2, 3, 4, 5, 6 и 1000.
Среднее значение равно 1,021 / 7 = 145,86 или приблизительно 146. Поскольку величина среднего, 146, намного больше, чем величина большинства наблюдений (первые 6), мы можем задаться вопросом, насколько хорошо она представляет положение данных в распределении.
На практике, хотя экстремальное значение (или выброс, от англ. ‘outlier’) в финансовых данных может быть редким значением в совокупности, оно также может отражать ошибку, допущенную при записи значения наблюдения или ошибку при формировании выборки из совокупности.
В частности, в последних двух случаях среднее арифметическое может вводить в заблуждение. Наиболее распространенный подход в таких случаях – использовать медиану вместо или в дополнение к среднему значению.
Медиана будет рассмотрена далее.
Другие подходы к обработке экстремальных значений включают применение вариаций среднего арифметического.
Усеченное среднее значение (от англ. ‘trimmed mean’ или ‘truncated mean’) вычисляется путем исключения указанного небольшого процента самых низких и самых высоких значений. Затем вычисляется среднее арифметическое из оставшихся значений.
Например, среднее значение, усеченное на 5%, отбрасывает наименьшие 2,5% и наибольшие 2,5% значений и вычисляет среднее из оставшихся 95% значений.
Усеченное среднее значение часто используется в спортивных соревнованиях, когда самые низкие и самые высокие оценки судей отбрасываются при подсчете оценки участника.
План урока:
Понятие выборки и генеральной совокупности
Среднее арифметическое выборки
Упорядоченный ряд и таблица частот
Размах выборки
Мода выборки
Медиана выборки
Ошибки в статистике
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:
Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.
В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.
Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.
Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
= 349:20 = 17,45.
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.
Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:
При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
2+3+1+1+2+2+1+2+2+1+1+2 = 20.
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.
Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
25 – 12 = 13,
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
9 – 8 = 1,
в то время как размах выборки второго спортсмена равен
10 – 6 = 4.
Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.
В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:
Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:
Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
(17+17):2 = 34:2 = 17.
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
(36+39+39+41+44+46+58+60+67+69):10 =
= 499:10 = 49,9 кг.
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
69 – 36 = 33 кг.
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
(44+46):2 = 90:2 = 45 кг.
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.


























