Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.
В чем проблема?
Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.
Давайте обратимся к классическому примеру со средней зарплатой.
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
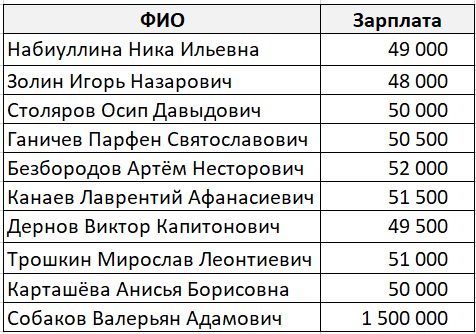
Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
Формула:
![]()
- x – среднее арифметическое;
- xn – конкретное значение;
- n – количество значений.
Плюсы:
- Хорошо работает при нормальном распределении значений в выборке;
- Легко вычислить;
- Интуитивно понятно.
Минусы:
- Не дает реального представления о распределении значений;
- Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
Формула:
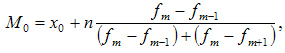
- M0 – мода;
- x0 – нижняя граница интервала, который содержит моду;
- n – величина интервала;
- fm– частота (сколько раз в ряду встречается то или иное значение);
- fm-1 – частота интервала предшествующего модальному;
- fm+1 – частота интервала следующего за модальным.
Плюсы:
- Прекрасно подходит для получения представления об общественном мнении;
- Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
- Проста для понимания.
Минусы:
- Моды может просто не быть (нет повторов);
- Мод может быть несколько (многомодальное распределение).
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
Формула:
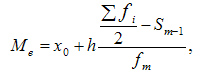
- Me – медиана;
- x0 – нижняя граница интервала, который содержит медиану;
- h – величина интервала;
- f i – частота (сколько раз в ряду встречается то или иное значение);
- Sm-1 – сумма частот интервалов предшествующих медианному;
- fm – число значений в медианном интервале (его частота).
Плюсы:
- Дает самую реалистичную и репрезентативную оценку;
- Устойчива к выбросам.
Минусы:
- Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
СРЗНАЧ(число1;[число2];…)— функция для определения среднего арифметического;МОДА.ОДН(число1;[число2];...)— функция моды (в более старых версиях Excel использоваласьМОДА(число1;[число2];...));МЕДИАНА(число1;[число2];...)— функция для поиска медианы.
И вот какие значения у нас получились:
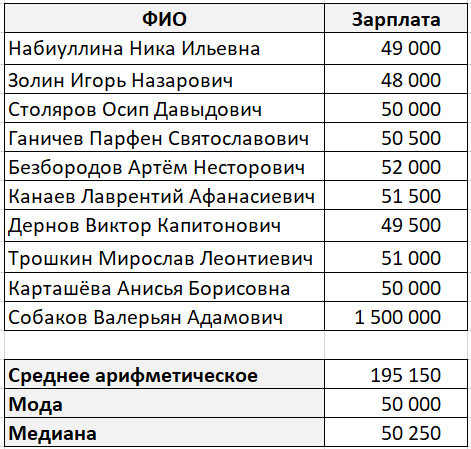
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция AVG.
И чтобы ее использовать достаточно написать вот такой запрос:
/* Здесь и далее salary - столбец с зарплатами, а employees - таблица сотрудников в нашей базе данных */ SELECT AVG(salary) AS 'Средняя зарплата' FROM employees
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
Напишем запрос:
/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */ SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты' FROM employees GROUP BY salary ORDER BY COUNT(*) DESC
Вычисляем медиану на SQL
Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей PERCENTILE_CONT.
Выглядит все это так:
/* В данном случае процентиль 0.5 и будет являться медианой */
SELECT TOP(1) PERCENTILE_CONT(0.5)
WITHIN GROUP (ORDER BY salary)
OVER() AS 'Медианная зарплата'
FROM employees
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Какой способ все-таки использовать?
Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:
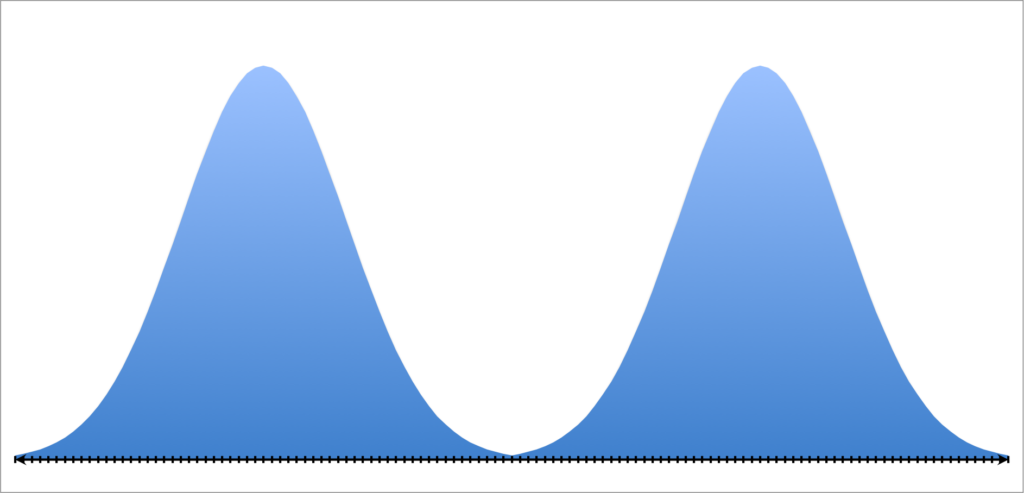
На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.
В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.
А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.
Вывод:
При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.
Окончательный выбор меры центральной тенденции всегда лежит на аналитике.
Полезные ссылки:
- SQL и теория вероятностей (YouTube)
- Анализ нормальности распределения данных (YouTube)
- Меры центральной тенденции
- Об авторе
- Свежие записи
Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.
Введение[править | править код]
Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и 

Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры[править | править код]
- Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
- Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
Непрерывная случайная величина[править | править код]
Если существует интеграл от некоторой функции 
![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
Здесь для определения отрезка ![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)


Линейное преобразование[править | править код]
Линейно преобразованный набор данных 





Некоторые проблемы применения среднего[править | править код]
Отсутствие робастности[править | править код]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент[править | править код]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 60 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 60 %) / 2 = 25 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается 20 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 60 % — это 60 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 60 %, они в конце второго года стоят $43,2. Арифметическое среднее этого роста 25 %, но, поскольку акции выросли за 2 года всего на $13,2, средний рост в 20 % даёт конечный результат $43,2:
$30 × (1 – 0,1)*(1 + 0,6) = $30 × (1 + 0,2)*(1 + 0,2) = $43,2. Если же использовать таким же образом среднее арифметическое значение 25 %, мы не получим фактическое значение: $30 × (1 + 0,25)*(1 + 0,25) = $46,875.
Сложный процент в конце 2 года: 90 % * 160 % = 144 %, то есть общий прирост 44 %, а среднегодовой сложный процент 
Таким образом среднегодовой прирост рассчитывается по формуле среднего геометрического

Направления[править | править код]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Примечания[править | править код]
- ↑ Cantrell, David W., «Pythagorean Means» Архивная копия от 22 мая 2011 на Wayback Machine from MathWorld
См. также[править | править код]
- Арифметическая пропорция
- Арифметическая прогрессия
- Неравенство Швейцера
- Среднее арифметическое взвешенное
Ссылки[править | править код]
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
- Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика
13 мая 2021 г.
Арифметика может помочь людям множеством способов, некоторые из которых более распространены, чем другие. Одной из наиболее распространенных форм арифметики является вычисление среднего значения, которое является средним значением набора чисел. Понимание того, что такое среднее значение, а также как его вычислить, может помочь вам проводить расчеты, такие как средние оценки, средние денежные значения и другие полезные числовые значения. В этой статье мы объясним, что такое среднее значение набора чисел, покажем вам, как вычислить среднее значение, и опишем ситуации, в которых может потребоваться вычисление среднего значения.
Какое значение?
Среднее значение — это среднее числовое значение набора чисел. Люди могут использовать среднее значение для расчета средней оценки из набора оценок за тест или затрат в месяц для личных бюджетов. В отличие от медианы или моды, среднее значение является более традиционным методом расчета среднего. Среднее значение не обязательно приводит к одному из заданных чисел, которое появляется в наборе, который вы вычисляете.
Почему важно знать среднее значение?
Знание того, как рассчитать среднее значение, важно, потому что вы можете использовать его во многих статистических, математических и часто встречающихся жизненных ситуациях. Вы можете взять среднее значение своих оценок, расходов или общих средних значений, найдя среднее значение. Знание среднего может помочь свести к минимуму ошибку при прогнозировании любого отдельного значения в ваших данных. Среднее также может применяться к нескольким типам и типам чисел, например к денежным значениям. Знание того, как вычислить среднее значение, гарантирует, что ваши данные непротиворечивы и точны.
Как рассчитать среднее значение?
Формула для вычисления среднего значения набора чисел выглядит следующим образом:
(Сложение чисел)/общее число в наборе = среднее
Например, среднее числового набора 1, 2, 3, 4 и 5 выглядит следующим образом:
1 + 2 + 3 + 4 + 5 = 15
(15)/5 = 3
Следовательно, среднее значение равно 3 для этого набора чисел.
В чем разница между средним и медианой?
Разница между средним значением и медианой заключается в формуле для каждого из них. Среднее значение — это среднее значение набора чисел, а медиана — это расчет, используемый для определения середины набора чисел. Преимущества нахождения медианы включают тот факт, что экстремальные выбросы в наборе данных не влияют на медиану так сильно, как на среднее значение. Если вы хотите найти среднее значение набора чисел, включающего один или несколько экстремальных выбросов, вы можете найти медиану вместо среднего для более точного результата.
Формула медианы выглядит следующим образом:
Либо: если общее количество чисел в наборе нечетное, среднее число в наборе является медианой.
Или: если общее количество чисел в наборе четное, возьмите два средних числа, сложите их и разделите это число на два.
Например, если вы хотите вычислить медиану набора 2, 3, 4, 5 и 6, вы должны просто извлечь среднее число, которое в данном случае равно 4.
Чтобы вычислить медиану набора 2, 3, 4 и 5, вы складываете два средних числа и делите это число на два:
(3 + 4)/2 = 3,5
Медиана = 3,5
Связанный: Как рассчитать операционный доход
Каковы некоторые примеры ситуаций, когда вы могли бы использовать среднее значение?
Есть много ситуаций, в которых вы бы использовали среднее значение набора чисел для вычисления чего-либо. Некоторые из этих ситуаций включают следующее:
Средние оценки
Джейкоб хочет, чтобы в его табеле успеваемости по математике за неделю было не менее 85 баллов. Чтобы понять общую оценку, которую он получил за последнюю неделю, он подсчитывал среднее значение своих баллов. Оценки, которые Джейкоб получил на прошлой неделе, были 87, 65, 93, 89 и 72.
Чтобы рассчитать средний балл Джейкоба за эту неделю, он воспользовался формулой среднего:
(87 + 65 + 93 + 89 + 72)/5 = Среднее
Среднее значение = 81,2
Это означает, что средняя оценка Джейкоба за неделю составляет 81,2. Джейкоб не достиг своей цели на этой неделе.
Статистические средние
Карл владеет кинотеатром и хочет рассчитать статистику количества положительных отзывов о конкретном фильме, оставленных людьми в течение недели, чтобы определить, следует ли ему продолжать смотреть этот фильм. Для этого он подсчитывает среднее количество положительных отзывов, которые люди оставили после просмотра фильма в его местном кинотеатре. Из 100 человек, зарегистрированных каждый день, 47 оставили положительный отзыв в понедельник, 26 оставили положительный отзыв во вторник, 59 оставили положительный отзыв в среду, 93 оставили положительный отзыв в четверг и 82 оставили положительный отзыв в пятницу.
Он вычисляет свою среднюю формулу следующим образом:
(47 + 26 + 59 + 93 + 82)/5 = Среднее
Среднее значение = 61,4
В среднем более половины зрителей оставили положительные отзывы об этом фильме, поэтому Карл продолжает показывать этот фильм в своем кинотеатре.
Результаты исследований
Венди — директор школы. Она провела опрос, который показал, что 73 из 100 учеников ее школы предпочитают использовать в классе учебники, а не планшеты. Тем не менее, она проводит опрос еще пять раз в этом году, чтобы убедиться, что ее результаты точны. Результаты были 89, 74, 62, 82 и 90. Чтобы вычислить среднее значение, она применяет следующую формулу:
(73 + 89 + 74 + 62 + 82 + 90)/6 = Среднее
Среднее значение = 78,3
Таким образом, среднее количество учеников, предпочитающих учебники, составляет 78,3 из 100. Венди решает отдать предпочтение обучению по учебникам, а не по планшетам в классах своей школы.
Средняя посещаемость
Барбара владеет местным театром, в котором недавно ставили спектакль в течение пяти вечеров, и она хочет знать, сколько людей в среднем посещало спектакль каждый вечер. В первый вечер пришло 200 человек, во второй — 340, в третий — 220, в четвертый — 345, а в последний вечер — 456 человек. Она применяет формулу среднего к этим данным следующим образом:
(200 + 340 + 220 + 345 + 456)/5 = Среднее
Среднее значение = 312,2
В результате среднего расчета Барбара обнаружила, что средняя посещаемость составляет чуть более 312 посетителей за ночь, что она считает успехом.
Больше всего в эк.
практике приходится употреблять среднюю
арифметическую, которая может быть
исчислена как средняя арифметическая
простая и взвешенная.
Средняя
арифметическая (СА)
-наиболее
распространенный вид средних. Она
применяется в тех случаях, когда объем
варьирующего признака для всей
совокупности является суммой значений
признаков отдельных ее единиц. Для
общественных явлений характерна
аддитивность (суммарность) объемов
варьирующего признака, этим определяется
область применения СА и объясняется
ее распространенность как обобщающего
показателя, напр:
общий фонд з/ п – это сумма з/п всех
работников.
Чтобы исчислить
СА, нужно сумму всех значений признаков
разделить на их число. СА
примен-ся в 2 формах.
Рассмотрим сначала простую арифметическую
среднюю.
1-СА простая
(исходная, определяющая форма) равна
простой сумме отдельных значений
осредняемого признака, деленной на
общее число этих значений (применяется
когда имеются несгруппированные инд.
значения признака):
Произведенные
вычисления могут быть обобщены в
следующую формулу:
![]()
![]() (1)
(1)
где
![]() — среднее значение варьирующего
— среднее значение варьирующего
признака, т. е. средняя арифметическая
простая;
![]() означает суммирование,
означает суммирование,
т. е. сложение отдельных признаков;
x —
отдельные значения варьирующего
признака, которые называются вариантами;
n
— число
единиц совокупности
Пример1,
требуется найти среднюю выработку
одного рабочего (слесаря), если известно,
сколько деталей изготовил каждый из 15
рабочих, т.е. дан ряд инд. значений
признака, шт.: 21;
20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.
СА простая
рассчитывается по формуле(1),шт.:
![]()
Пример2.
Рассчитаем СА на основании условных
данных по 20 магазинам, входящим в торговую
фирму (табл. 1).
Таблица.1
Распределение магазинов торговой фирмы “Весна” по торговой площади, кв. М
|
№ магазина |
Площадь |
№ магазина |
Площадь |
|
1 |
60 |
11 |
50 |
|
2 |
80 |
12 |
120 |
|
3 |
40 |
13 |
100 |
|
4 |
100 |
14 |
60 |
|
5 |
60 |
15 |
80 |
|
б |
70 |
16 |
60 |
|
7 |
50 |
17 |
70 |
|
8 |
120 |
18 |
40 |
|
9 |
100 |
19 |
50 |
|
10 |
60 |
20 |
50 |
Для вычисления
средней площади магазина (![]() )
)
необходимо сложить площади всех магазинов
и полученный результат разделить на
число магазинов:
![]()
Т.о., средняя площадь
магазина по этой группе торговых
предприятий составляет 71 кв.м.
Следовательно,
чтобы определить СА простую, нужно сумму
всех значений данного признака разделить
на число единиц, обладающих этим
признаком.
2
где
f1,
f2,
… ,fn
– веса
(частоты повторения одинаковых
признаков);
– сумма произведений
величины признаков на их частоты;
– общая численность
единиц совокупности.
–СА взвешенная
– средняя из вариантов,
которые повторяются различное число
раз, или, как говорят, имеют различный
вес. В качестве весов выступают численности
единиц в разных группах совокупности
(в группу объединяют одинаковые варианты).
СА взвешенная
– средняя
сгруппированных величин x1,
x2,
.., xn,
–
вычисляется:  (2)
(2)

Где х — варианты;
f— частота (вес).
СА взвешенная
есть частное от деления суммы произведений
вариантов и соответствующих им частот
на сумму всех частот.
Частоты (f)
фигурирующие в формуле СА, принято
называть весами,
вследствие чего СА, вычисленная с учетом
весов, и получила название взвешенной.
Технику вычисления
СА взвешенной проиллюстрируем на
рассмотренном выше примере 1. Для этого
сгруппируем исходные данные и поместим
их в табл.
Средняя из
сгруппированных данных определяется
следующим образом: сначала перемножают
варианты на частоты, затем складывают
произведения и полученную сумму делят
на сумму частот.
Таблица
По формуле (2) СА
взвешенная равна, шт.:
![]()
Распределение
рабочих по выработке деталей
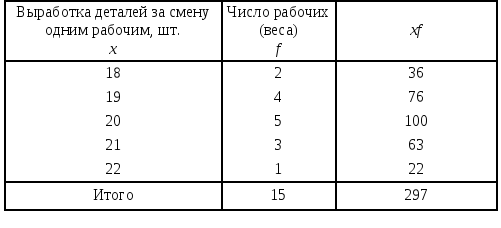
П
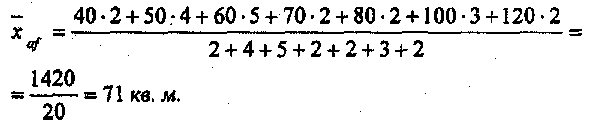
риведенные в предыдущем примере 2
данные можно объединить в однородные
группы, которые представлены в табл.Таблица
Распределение
магазинов фирмы “Весна” по торговой
площади, кв. м
|
Площадь магазинов |
40 |
50 |
60 |
70 |
80 |
100 |
120 |
|
Число магазинов |
2 |
4 |
5 |
2 |
2 |
3 |
2 |
Т.о., результат
получился тот же самый. Однако это уже
будет величина средняя арифметическая
взвешенная.
В предыдущем
примере мы вычисляли арифметическую
среднюю при условии, что известны
абсолютные частоты (численность
магазинов). Однако в ряде случаев
абсолютные частоты отсутствуют, а
известны относительные частоты, или,
как принято их называть, частости,
которые показывают долю или удельный
вес частот во всей совокупности.
При расчетах СА
взвешенной использование частот
позволяет упрощать расчеты, когда
частота выражена большими, многозначными
числами. Расчет производится тем же
способом, однако, так как средняя величина
оказывается увеличенной в 100 раз,
полученный результат следует разделить
на 100.
Тогда формула
средней арифметической взвешенной
будет иметь вид:
![]()
где d
– частость,
т.е. доля каждой частоты в общей сумме
всех частот.
(3)
В нашем примере 2
сначала определяют удельный вес магазинов
по группам в общей численности магазинов
фирмы “Весна”. Так, для первой группы
удельный вес соответствует 10%
![]() .
.
Получаем следующие данныеТаблица3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):

(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.

(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):

Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:

(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле

(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:

Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.

- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12

(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13

(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)

8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)

(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.

Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке



![{displaystyle {overline {f(x)}}_{[a;b]}={frac {1}{b-a}}int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db0287956e28e4ced0b833809f5b0ed44aaa7339)

