Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Как считается среднее арифметическое?
Анонимный вопрос
30 октября 2018 · 97,9 K
Среднее арифметическое – это сумма всех чисел, подлежащих усреднению, деленная на их количество.
Для вычисления среднего арифметического необходимо выполнить следующие действия:
1. Сложить все числа, которые нужно усреднить.
2. Разделить полученную сумму на количество чисел.
Формула для вычисления среднего арифметического:
Среднее арифметическое = (a1 + a2 + … + an) / n
Где a1, a2, …, an – числа, которые нужно усреднить, а n – их количество.
309
Комментировать ответ…Комментировать…
Среднее арифметическое рассчитывается как сумма всех чисел, деленная на количество этих чисел. То есть, если у нас есть числа 1, 2, 3, то их среднее арифметическое будет (1+2+3)/3 = 2.
15,4 K
Спасибо большое за то что объяснили
Комментировать ответ…Комментировать…
> как читают средние арифметическое,Просто, берём числа 5, 7, 10
> мы их складываем
> 5+7+10 =22
> Потом умножаем на то количество цифер сколько их в уравнение, у нас их 3 значит
> 22 / 3 = 7 ,3
> Ответ:7,3 Читать далее
7,5 K
Комментировать ответ…Комментировать…
Мне интересны множество тем: от психологии до космоса…) · 31 окт 2018
Среднее арифметическое – самый простой, и потому часто используемый, показатель для сравнения данных, а также вычисления приемлимого значения.
Рассчитывается как частное от деления суммы значений массива данных на количество значений в массиве.
9,1 K
Комментировать ответ…Комментировать…
Найти среднее арифметическое можно таким способом:
например, у вас есть числа 5, 9 и 10. Для начала нам нужно сложить эти числа , всего получается 24. Всего у нас три числа, значит 24 нужно поделить на 3. Получается 8. (24:3=8)
2,7 K
Комментировать ответ…Комментировать…
Найти среднее арифметическое можно по такой схеме
Среднее арифметическое=сумма всех чисел:количество слагаемых.
Пример, найдем среднем арифметическое чисел 12,11 и 4
1.12+11+4=27=27:3(делим на три потому что у нас три слагаемых) =9
Среднее арифметическое равно 9
9,9 K
Комментировать ответ…Комментировать…
Что бы посчитать среднее арифметическое,нужно все числа сложить, а потом разделить на их численность.
Пример: 1,2,3
1)1+2+3=6
2)6:3=2.
Ответ:среднее арифметическое равно двум.
25,9 K
Комментировать ответ…Комментировать…
Среднее арифметическое значение можно вычилисть вот таким способом.
Допустим у вас есть три числа: 2, 8 и 12.
Нужно вычислить среднее арифметическое.
Сумма всех этих чисел равна 22.
Всего этих чисел три.
22 / 3 = 7,3 (это среднеарифметическое). Читать далее
462
22/3 не равно в точности 7,3. Получается, что и метод не объяснен, и пример неточный.
Комментировать ответ…Комментировать…
Загрузить PDF
Загрузить PDF
Чтобы вычислить среднее арифметическое в группе чисел, необходимо их сложить и разделить на количество чисел. В повседневной жизни среднее арифметическое может пригодиться, когда необходимо оценить ежемесячные расходы, узнать, сколько времени уходит на выполнение той или иной задачи, или определить количество людей на основе предыдущего посещения.
-
1
Найдите сумму чисел в данном ряду. Первым делом сложите все числа в числовом ряду. Предположим, вам дан ряд 1, 2, 3, and 6. В этом случае сумма будет составлять
.[1]
-
2
Разделите результат на количество чисел в ряду. Наш ряд состоит из четырех чисел, поэтому следует взять сумму, 12, и разделить ее на четыре.[2]
. Среднее арифметическое в этом ряду равняется 3.[3]
Реклама
-
1
Запишите среднее арифметическое в каждой категории. Прежде всего найдите среднее арифметическое каждой категории, сложив все числа в ряду и разделив на количество чисел. Например, вам требуется найти средневзвешенное значение для класса и даны следующие числа:[4]
- Среднее арифметическое домашней работы = 93 %
- Среднее арифметическое экзамена = 88 %
- Среднее арифметическое проверочной работы = 91 %
-
2
Запишите весовую категорию каждого среднего арифметического. Помните, что весовые категории должны в сумме составлять 100 %. Предположим, вам даны следующие весовые категории:
- Среднее арифметическое домашней работы = 30 % итоговой оценки
- Среднее арифметическое экзамена = 50 % итоговой оценки
- Среднее арифметическое проверочной работы = 20 % итоговой оценки
-
3
-
4
Сложите полученные результаты. Чтобы найти средневзвешенное значение, сложите все три результата:
. Средневзвешенное значение для этого ряда равняется
.
Реклама
Советы
- Пользуйтесь бумагой и ручкой, они упрощают жизнь в миллион раз.
Реклама
Об этой статье
Эту страницу просматривали 73 226 раз.
Была ли эта статья полезной?
Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.
Введение[править | править код]
Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и 

Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры[править | править код]
- Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
- Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
Непрерывная случайная величина[править | править код]
Если существует интеграл от некоторой функции 
![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
Здесь для определения отрезка ![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)


Линейное преобразование[править | править код]
Линейно преобразованный набор данных 





Некоторые проблемы применения среднего[править | править код]
Отсутствие робастности[править | править код]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент[править | править код]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 60 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 60 %) / 2 = 25 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается 20 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 60 % — это 60 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 60 %, они в конце второго года стоят $43,2. Арифметическое среднее этого роста 25 %, но, поскольку акции выросли за 2 года всего на $13,2, средний рост в 20 % даёт конечный результат $43,2:
$30 × (1 – 0,1)*(1 + 0,6) = $30 × (1 + 0,2)*(1 + 0,2) = $43,2. Если же использовать таким же образом среднее арифметическое значение 25 %, мы не получим фактическое значение: $30 × (1 + 0,25)*(1 + 0,25) = $46,875.
Сложный процент в конце 2 года: 90 % * 160 % = 144 %, то есть общий прирост 44 %, а среднегодовой сложный процент 
Таким образом среднегодовой прирост рассчитывается по формуле среднего геометрического

Направления[править | править код]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Примечания[править | править код]
- ↑ Cantrell, David W., «Pythagorean Means» Архивная копия от 22 мая 2011 на Wayback Machine from MathWorld
См. также[править | править код]
- Арифметическая пропорция
- Арифметическая прогрессия
- Неравенство Швейцера
- Среднее арифметическое взвешенное
Ссылки[править | править код]
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
- Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика
|
Формула среднего арифметического чисел? Среднее арифметическое нескольких чисел — это сумма этих чисел, делённая на их количество. x ср = S/n где: x ср — среднее арифметическое S — сумма чисел n — количество чисел. Например, нам нужно найти среднее арифметическое чисел 3, 4, 5 и 6. Для этого нам нужно их сложить и полученную сумму разделить на 4: (3 + 4 + 5 + 6) : 4 = 18 : 4 = 4,5. автор вопроса выбрал этот ответ лучшим Алсу – Ш 8 лет назад Мне, как математику, интересны вопросы по данному предмету. Начну с истории вопроса. Над средними величинами задумывались с древних времмен. Среднее арифметическое, среднее геометоическое, среднее гармоническое. Эти понятия предложены в древней Греции пифагорийцами. А теперь интересующий нас вопрос. Что же понимается под средним арифметичским нескольких чисел: Итак, для нахождения среднего арифметического чисел нужно прибавить все числа и разделить полученную сумму на количество слагаемых. Имеет место формула: Пример. Найти среднее арифметическое чисел: 100, 175, 325. Решение. Воспользуемся формулой нахождения среднего арифметического трех чисел (то есть вместо n будет 3; нужно сложить все 3 числа и разделить полученную сумму на их количество, т.е. на 3). Имеем: х=(100+175+325)/3=600/3=200. Ответ: 200. Арифметика считается самым элементарным разделом математики и изучает простые действия с числами. Поэтому и среднее арифметическое также находится очень просто. Начнем с определения. Среднее арифметическое – это величина, которая показывает какое число наиболее близко к истине при нескольких последовательных однотипных действиях. Например при беге на сто метров человек каждый раз показывает разное время, но средняя величина будет в пределах например 12 секунд. Нахождение среднего арифметического таким образом сводится в последовательному суммированию всех чисел определенного ряда (результатов забегов) и деление этой суммы на количество этих забегов (попыток, чисел). В виде формулы это выглядит так: Sариф = (Х1+Х2+..+Хn)/n Среднее арифметическое – это среднее число между несколькими числами. Например между числами 2 и 4 среднее число 3. Формула нахождения среднего арифметического такая: Нужно сложить все числа и разделить на количество этих чисел: Например у нас 3 числа: 2, 5 и 8. Находим среднее арифметическое: X=(2+5+8)/3=15/3=5 Область применения среднего арифметического достаточно широка. Например можно зная координаты двух точек отрезка найти координаты середины этого отрезка. Например координаты отрезка: (X1,Y1,Z1)-(X2,Y2,Z2). Обозначим середину этого отрезка координатами X3,Y3,Z3. Отдельно находим середину для каждой координаты: X3=(X1+X2)/2; Y3=(Y1+Y2)/2; Z3=(Z1+Z2)/2; Красивая поляна 8 лет назад Средне арифметическое число, это числа сложенные вместе и деленные на их количество, полученный ответ и есть средне арифметическое число. Например: Катя положила в копилку 50 рублей, Максим 100 рублей, а Саша положил в копилку 150 рублей. 50 + 100 + 150 = 300 рублей в копилке, теперь делим эту сумму на три (три человека положили деньги). Итак 300 : 3 = 100 рублей. Эти 100 рублей и будет средне арифметически, каждый из них положил в копилку. Есть такой простой пример: один человек ест мясо, другой человек ест капусту, а средне арифметически они оба едят голубцы. Таким же образом рассчитывают среднюю зарплату… Среднеарифметическое-это среднее значение из заданных… Т.е. по простому имеем количество палочек разной длины и хотим узнать их среднее значение.. Логично, что для этого мы их сводим вместе, получая длинную палку, а потом делим её на требуемое число частей.. Вот и выходит среднеарифметическое.. Вот так и выводится формула:Sa=(S(1)+..S(n))/n.. Птичка2014 8 лет назад Среднее арифметическое – это сумма всех значений и деленное на их количество. Например числа 2, 3 , 5, 6 . Нужно их сложить 2+ 3+ 5 + 6 = 16 16 делим на 4 и получаем ответ 4 . 4 и есть среднее арифметическое этих чисел. Azamatik 7 лет назад Средним арифметическим называют сумму чисел, разделенное на количество этих самых чисел. А найти среднее арифметическое очень просто. Как следует из определения мы должны взять числа, сложить их и разделить на их количество. Приведем пример: дается числа 1, 3, 5, 7 и нам надо найти среднее арифметическое этих чисел.
Итак, среднее арифметическое чисел 1, 3, 5 и 7 – это 4. tana76 7 лет назад Среднее арифметическое – среднее значение среди заданных показателей. Оно находится путем деления суммы всех показателей на их количество. Например, у меня есть 5 яблок весом 200, 250, 180, 220 и 230 грамм. Средний вес 1 яблока находим так:
Это наиболее часто применяемый в статистике показатель. Alen4uk 7 лет назад Это мы знаем со школьной скамьи. У кого был хороший учитель по математике, то запомнить это нехитрое действие можно было с первого раза. При нахождении среднего арифметического необходимо сложить все имеющиеся числа и разделить на их количество. Например, я купила в магазине 1 кг яблок, 2 кг бананов, 3 кг апельсинов и 1 кг киви. Сколько килограммов в среднем я купила фруктов. 1+2+3+1=7. 7/4= 1,8 килограммов. Это и будет среднеарифметическим значением. Даксплячи Учлинзайх 7 лет назад Помню как итоговую контрольную по математике сдавал Так там нужно было среднее арифметическое найти. Хорошо что добрые люди подсказали что делать, иначе беда. Например у нас 4 числа. Складываем числа и делим на их количество (в данном случае 4) Например цифры 2,6,1,1. Складываем 2+6+1+1 и делим на 4 = 2.5 Как видите ничего сложного. Так что среднее арифметическая – это среднее значение всех чисел. Знаете ответ? |
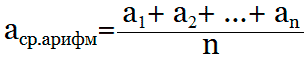













![{displaystyle {overline {f(x)}}_{[a;b]}={frac {1}{b-a}}int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db0287956e28e4ced0b833809f5b0ed44aaa7339)



