Крайне неудобно анализировать множество значений за ряд периодов, поэтому целесообразнее вычислять средний показатель роста (убыли) определенного параметра. Средний темп роста является показателем статистической динамики для анализа явлений и процессов (интенсивности изменения и скорости роста) в различных областях жизнедеятельности: финансовой сфере, сфере производства и торговли, статического анализа и пр.
Коэффициент, отражающий средний за ряд периодов рост показателя в процентном измерении.
Структура формулы:
- значение на начало измерения;
- значение в конце измерения;
- промежуточные показания, через равные интервальные моменты.
T‾=n−1TсрT1100%overline {T}=^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}100%
Tср=∑1nTkntext{Tср}=sum _1^n frac{T_k}{n}
где T1T_1 – начальное значение показателя,
TkT_k – значение показателя за период k(1…n)k (1…n),
nn – число периодов расчета,
Tсрtext{Tср} – среднее значение показателя.
Алгоритм расчета:
- Определение периода сравнения nn;
- Вычисление суммы параметров за период nn;
- Нахождение среднего параметра путем деления суммы (п.2) на число периодов nn;
- Вычисление среднего темпа роста как корень степени n−1n-1 от частного среднего и начального T$$ на 100%.100%.
Определить средний темп роста прибыли фирмы по следующим данным:
| Месяц | Сумма |
|---|---|
| Январь | 142000 руб. |
| Февраль | 146000 руб. |
| Март | 136000 руб. |
| Апрель | 151000 руб. |
| Май | 163000 руб. |
| Июнь | 113000 руб. |
| Июль | 122000 руб. |
| Август | 125000 руб. |
| Сентябрь | 132000 руб. |
| Октябрь | 156000 руб. |
| Ноябрь | 167000 руб. |
| Декабрь | 178000 руб. |
Решение
- Период n=12n = 12;
- Сумма прибыли за год:
142000+146000+136000+151000+163000+113000+122000+125000+132000+156000+167000+178000=1731000142000+146000+136000+151000+163000+113000+122000+125000+132000
+156000+167000+178000 = 1731000 руб.
- Средняя прибыль за год:
Tср=173100012=144250text{Tср}=173100012=144250руб.
- Средний темп роста:
T‾=14425014200011100%=1,00143⋅100%=100,143%overline{T}=sqrt[11]{frac{144250}{142000}}100%=1,00143cdot100%=100,143%
Ответ: Средний темп роста прибыли составил $100,143%$ в год.
Найти значение выручки в апреле, если известно, что в январе было заработано 6132 тыс. руб., в феврале – 5861 тыс. руб., в марте – 6318 тыс. руб. Показатель среднего темпа роста за 4 месяца – 113%.
Решение
- Средний темп роста
T‾=n−1TсрT1100%=113%overline {T}=^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}100%=113%
n−1TсрT1=1,13^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}=1,13
4−1Tср6132=1,13^{4-1} sqrt{frac{text{Tср}}{6132}}=1,13
Tср6132=1,133frac{text{Tср}}{6132}=1,13^3
Tср6132=1,4429frac{text{Tср}}{6132}=1,4429
Tср=8847,86text{Tср}=8847,86 тыс. руб.
- Средняя выручка (XX – выручка за апрель):
Tср=∑1nTkn=8847,86text{Tср}=sum _1^n frac{T_k}{n}=8847,86
∑1nTk4=8847,86frac{sum_{1}^{n}T_k}{4}=8847,86
6132+5861+6318+X4=8847,866132+5861+6318+X4=8847,86
6132+5861+6318+X=35391,446132+5861+6318+X=35391,44
X=35391,44−6132−5861−6318=17080,44X=35391,44-6132-5861-6318=17080,44 тыс. руб.
Ответ: Выручка в апреле 17080,4417080,44 тыс. руб.
Средний темп роста является многогранным показателем, позволяющим наглядно отразить результаты изменения тех или иных экономических данных. По результатам анализа компания может оценить динамику роста, выявить влияющие факторы и спрогнозировать будущие показатели с учетом сезонных изменений.
Тест по теме «Формула среднего темпа роста»
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат

Гражданское право – работа с недвижимостью. договорная работа, наследственное право, банкротство.
Важнейшим показателем эффективности производства в анализе финансовой ситуации компании является показатель темпа роста. Поговорим об особенностях его расчета.
Как рассчитать темп роста: формула
Что называют снижением темпа роста цен?
Подробнее
Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.
Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.
Как рассчитать темп роста в процентах – формула:
ТР = Пт / Пб х 100%,
где Пк и Пб – показатели значений текущего и базового периодов.
Узнайте, может ли темп роста быть отрицательной величиной.
Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:
-
ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;
-
ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;
-
ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.
Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:
|
Объем выпуска в тыс. руб. |
Расчет (Пт / Пб х 100%) |
|
|
2017 (Пб) |
2018 (Пт) |
|
|
600 |
800 |
133,3% |
|
600 |
600 |
100% |
|
600 |
400 |
66,7% |
Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.
Узнайте, чем отличается темп роста от темпа прироста.
Как рассчитать цепные темпы роста
Рассмотрим пример расчета базисного и цепного темпов роста:
|
Период |
Объем в тыс.руб. |
Темп роста в % |
|
|
базисный |
цепной |
||
|
1 кв. |
300 |
100 |
– |
|
2 кв. |
310 |
103,3 (310 / 300) |
103,3 (310 / 300) |
|
3 кв. |
280 |
93,3 (280 / 300) |
90,3 (280 / 310) |
|
4 кв. |
360 |
120 (360 / 300) |
128,6 (360 / 280) |
Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).
Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.
Как рассчитать темпы прироста
Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:
∆ ТР = (Птек – Пбаз) / Пбаз х 100%
Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:
∆ ТР = (Птек – Ппр.п) / Ппр. п х 100%.
Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.
Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:
|
Период |
Темпы прироста |
|
|
базисные |
цепные |
|
|
1 кв. |
– |
– |
|
2 кв. |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
|
3 кв. |
– 6,7% (93,3 – 100) или ((280 – 300) / 300 х 100) |
-9,7% (90,3 – 100) или ((280 – 310) / 310 х 100) |
|
4 кв. |
20% (120 – 100) или (( 360 – 300) / 300 х 100) |
28,6% (128,6 – 100) или ((360 – 280) / 280 х 100) |
Анализируя результаты вычислений, экономист может сделать вывод:
-
Прирост объемов наблюдался во 2-м и 4-м кварталах, причем во 2-м он был наименьшим (3,3%). В 3-м квартале объем выпуска сократился на 6,7% в сравнении с показателями начала года;
-
Цепные темпы прироста обнаружили более глубокие колебания: объемы 3-го квартала снизились по отношению к показателям 2-го на 9,7%. Зато выпуск товаров в 4-м квартале вырос почти на треть в сравнении с итогами 3-го квартала. Столь существенные изменения в объемах производства могут свидетельствовать о сезонности выпускаемых продуктов, перебоях в снабжении необходимым сырьем или других причинах, которые исследует аналитик.
Как рассчитать средний темп роста
Средний темп роста – обобщающая характеристика уровня изменений. Расчет средних темпов роста и прироста также разграничивают на базисные и цепные. Для определения среднего темпа роста расчетные показатели по периодам складывают и делят на количество периодов. Таким же образом находят и средние темпы приростов. Вернемся к предыдущему примеру, рассчитав средние значения базисных темпов роста и прироста, а также аналогичных цепных показателей.
|
Показатель |
Значение в % |
Расчет |
|
Средний темп роста (базисный) |
105,5 |
(103,3 + 93,3 + 120) / 3 |
|
Средний темп прироста (базисный) |
5,5 |
(3,3 – 6,7 + 20) / 3 |
|
Средний темп роста (цепной) |
107,4 |
(103,3 + 90,3 + 128,6) / 3 |
|
Средний темп прироста (цепной) |
7,4 |
(3,3 – 9,7 + 28,6) / 3 |
Полученные цифры свидетельствуют о том, что в среднем с начала года объемы выпуска выросли на 5,5%, а в поквартальной привязке рост составил 7,4%.
Читайте также: Экспресс-анализ финансового состояния предприятия

Специализация: Гражданское право – работа с недвижимостью. договорная работа, наследственное право, банкротство.
Окончила в 2005 г. Тверской государственный университет, юридический факультет, специальность-юриспруденция.
Юрист в сфере недвижимости:составление договоров, регистрация в Росреестре прав и сделок,оформление наследственных прав,
сопровождение сделок с недвижимым имуществом,судебный опыт по делам,связанным с признанием прав на недвижимость.
Имеется опыт работы помощником арбитражного управляющего.
5.1. Методические указания и решение типовых задач
Числовые значения
того или иного статистического показателя,
составляющие ряд динамики, называют
уровнями ряда
и обозначают черезy.
При анализе рядов
динамики необходимо проследить за
направлением и размером изменений
уровней во времени. С этой целью
рассчитывают следующие показатели.
1. Абсолютные
приросты уровней (разность между
двумя уровнями):
цепныеуц
= уi – уi-1;
(5.1)
и базисные уб
= уi –у0. (5.2)
2. Темпы роста
(изменения) ТР– относительные
показатели, рассчитываемые как отношение
двух уровней ряда. Темпы роста могут
бытьцепными, если каждый уровень
ряда сопоставляется с предыдущим:
![]() ,
,
(5.3)
и
базисными, когда каждый уровень
ряда сопоставляется с уровнем одного
какого-то периода (часто это начальный
– базисный – уровень ряда):
![]() .
.
(5.4)
Темпы роста как
относительные величины могут выражаться
в виде коэффициентов, т.е. простого
кратного отношения (база сравнения
принимается за единицу), и в процентах
(база сравнения принимается за 100 единиц).
3. Темпы прироста
(снижения) уровнейТПр– относительные
показатели, показывающие, на сколько
процентов данный уровень (y)
больше (или меньше) другого, принимаемого
за базу сравнения.
Темп прироста
можно рассчитать двумя способами:
1) путем вычитания
100% из темпа роста:
ТПр
=ТР -100%; (5.5)
2) как процентное
отношение абсолютного прироста к тому
уровню, по сравнению с которым рассчитан
абсолютный прирост:
![]() .
.
(5.6)
Методы расчета
среднего уровняряда динамики
зависят от его вида и способов получения
статистических данных.
В интервальном
ряду с равностоящими во времени
уровнями расчет производится по формуле
средней арифметической простой
![]() ,
,
(5.7)
где
п– число уровней ряда.
Для интервального
ряда с разными временными интерваламисредний уровень вычисляется по формуле
средней взвешенной
![]() ,
,
(5.8)
где ti– время, в течение которого уровеньyсчитается неизменным.
Для моментного
ряда, содержащегоnуровнейс равнымипромежутками
между датами (моментами), средний уровень
определяется по формуле
 .
.
(5.9)
Эта средняя известна
в статистике как средняя хронологическая
простая.
Для неравностоящих
уровней моментного ряда средняя
рассчитывается по формуле средней
хронологической взвешеннной:
![]() .
.
(5.10)
Средний абсолютный
приростопределяется как
![]()
(5.11)
или
![]() ,
,
(5.12)
где п– число
периодов.
Средний темп
ростарассчитывается из выражений
![]() ,
,
(5.13)
где
п– число темпов роста, аП–
знак произведения,
или
![]() .
.
(5.14)
Средний темп
прироста вычисляется по формуле
![]() .
.
(5.15)
Абсолютное
значение одного процента прироста (А1%)
определяется из выражения
![]()
(5.16)
или
|А1%|может быть исчислен как одна
сотая часть предыдущего уровня.
Среднее абсолютное
значение одного процента прироста за
несколько (п) лет рассчитывается по
формуле
![]() .
.
(5.17)
Пример 5.1
Пусть
имеются следующие данные о производстве
зерна в одном из хозяйств за 5 лет (табл.
5.1).
Таблица 5.1
|
Год |
2002 |
2003 |
2004 |
2005 |
2006 |
|
Производство зерна, |
50 |
54 |
62 |
70 |
80 |
Рассчитайте:
-
средний
уровень за 5 лет; -
ежегодные
абсолютные приросты; -
ежегодные
темпы роста; -
среднегодовой
темп роста за 4 года – с 2003 по 2006 г.; -
темп
прироста (цепной) за 2006 г.; -
абсолютное
значение одного процента прироста для
2006 г.
Решение
1. Так как это
интервальный ряд, то средний уровень
ряда (среднегодовое производство зерна)
определим как среднюю арифметическую
простую:
![]() тыс. ц.
тыс. ц.
2. Ежегодные
абсолютные приросты находим как цепную
разность между двумя уровнями:
для
2003 г. Δу1
= 54 – 50 = 4 тыс. ц;
для 2004 г. Δу2= 62 – 54 = 8 тыс. ц;
для 2005 г. Δу3= 70 – 62 = 8 тыс. ц;
для 2006 г. Δу4= 80 – 70 = 10 тыс. ц.
3. Ежегодные темпы
роста (цепные) находим как отношение
уровня каждого года к предыдущему:
для 2003 г. ТР1 =
54 / 50 = 1,08 = 108%;
для 2004 г. ТР2 =
62 / 54 = 1,148 = 114,8%;
для 2005 г. ТР3= 70 / 62 = 1,129 = 112,9%;
для 2006 г. ТР4 =
80 / 70 = 1,143 = 114,3%.
4. Среднегодовой
темп роста можно рассчитать по формуле
(5.13) как среднюю геометрическую из
годовых темпов роста
![]()
либо
по формуле (5.14)
![]() .
.
По первой формуле
![]() .
.
По второй формуле
![]() ,
,
т.е.
среднегодовой темп роста за 4 года (с
2003 по 2006 г.) равен 112,5%.
5. Темп прироста
определяем по формуле (5.5):
ТПр= 114,3%-100%=14,3%.
6. Абсолютное
значение одного процента прироста для
2006 г. определяется как одна сотая
предыдущего уровня:
А1%=70
тыс. ц / 100=0,7 тыс. ц.=700 ц
или
по формуле (5.16):
А1%=10 тыс. ц / 14,3%=700
ц.
Пример 5.2
Определите время,
в течение которого ряд с бόльшим средним
показателем динамики, но меньшим
начальным уровнем, догонит другой ряд
с меньшим средним показателем динамики,
но с бόльшим начальным уровнем.
Преобразуем формулу
(5.14), обозначив
![]() через
через![]() :
:
![]() .
.
Тогда
![]() .
.
Необходимо
определить, когда
![]() .
.
Решение
![]() .
.
Прологарифмируем:
![]()
Отсюда
![]()
![]() .
.
Если
![]() ,
,![]() и
и![]() ,
,![]() ,
,
то
![]() .
.
Следовательно,
через 11 лет уровень второго ряда
сравняется с уровнем первого ряда.
Пример 5.3
Имеются
данные о производстве продукции за
2003-2005 гг., млн руб. (табл. 5.2).
Таблица 5.2
|
Годы |
2003 г. |
2004 г. |
2005 г. |
|
Произведено продукции |
2220 |
2265 |
2360 |
Определите
среднегодовое производство продукции.
Решение
Среднегодовое
производство продукции за 2003-2005 гг.
будет определяться по формуле (5.7):
![]() млн
млн
руб.
Пример 5.4
Имеются
следующие данные об остатках сырья и
материалов на складе предприятия, млн
руб.:
на
1/I
– 400; на 1/II
– 455; на 1/IV
– 460.
Определите
среднемесячный остаток сырья и материалов
на складе предприятия за I
квартал.
Решение
По
условию задачи имеем моментный ряд
динамики с равными интервалами, поэтому
средний уровень ряда будет исчислен по
формуле средней хронологической простой
(5.9):
![]() млн руб.
млн руб.
Пример 5.5
Имеются
следующие данные о товарных запасах
розничного торгового предприятия за
2004 г. (табл. 5.3).
Таблица 5.3
|
1января |
1мая |
1 августа |
1 января 2005 г. |
|
61,1 |
57,5 |
51,3 |
74,7 |
Определите средний
уровень товарных запасов.
Решение
Число месяцев
между приведенными датами 4, 3, 5.
Средний
уровень товарных запасов за год для
моментного ряда динамики с неравными
интервалами вычислим по формуле средней
хронологической взвешенной (5.10):
![]() .
.
Важным
направлением в исследовании закономерностей
динамики социально-экономических
процессов является изучение общей
тенденции развития (тренда).
Наиболее
распространенными методами выделения
тренда являются метод скользящей средней
и аналитический метод.
Метод скользящей
средней заключается в том, что вычисляется
средняя величина из определенного
количества уровней (например, четырех)
с отбрасыванием при вычислении каждой
новой скользящей средней одного уровня
слева и присоединением одного уровня
справа:
![]() ;
;
![]() и т.д.
и т.д.
Скользящая средняя
дает более или менее плавное изменение
уровней ряда.
Пример 5.6
Имеются
данные о потреблении овощей по области
в 1997-2005 гг. на одного человека в месяц,
кг (у) (табл. 5.4).
Таблица 5.4
|
1997 г. |
1998 г. |
1999 г. |
2000 г. |
2001 г. |
2002 г. |
2003 г. |
2004 г. |
2005 г. |
|
10,0 |
10,7 |
12,0 |
10,3 |
12,9 |
16,3 |
15,6 |
17,8 |
18 |
Выявим
основную тенденцию потребления овощей
методом скользящей средней. Рассчитаем
трехлетние скользящие средние:
![]() кг;
кг;
![]() и т.д.
и т.д.
Получим
ряд (табл. 5.5).
Таблица 5.5
|
1998 г. |
1999 г. |
2000 г. |
2001 г. |
2002 г. |
2003 г. |
2004 г. |
|
10,9 |
11,0 |
11,8 |
13,2 |
15,9 |
16,6 |
17,1 |
Таким
образом, выявилась явная тенденция к
росту потребления овощей.
Получить
обобщенную статистическую оценку
тенденции развития явления (тренда)
можно методом аналитического выравнивания.
В этом случае ряд динамики выражается
математической зависимостью уровней
ряда y
от времени t:
y=f(t).
Рекомендуется
при
![]() (равномерное
(равномерное
развитие) использовать модели типа
![]() .
.
(5.18)
При равноускоренном
(равнозамедленном) развитии с постоянными
темпами прироста
![]() используется парабола второго порядка
используется парабола второго порядка
![]() .
.
(5.19)
Для развития с
переменным ускорением (замедлением)
используется парабола третьего порядка
![]() .
.
(5.20)
При
стабильных темпах роста
![]() развитие идет по экспоненте и отображается
развитие идет по экспоненте и отображается
показательной функцией
![]() .
.
(5.21)
Для
определения параметров математических
моделей применяется способ отсчета
времени от условного начала, при этом
![]() .
.
При
этом для прямолинейной функции:
![]()
![]()
![]() ; (5.22)
; (5.22)
![]() ; (5.23)
; (5.23)
для
показательной функции:
![]()
![]() ;
;
![]() ;
;
(5.24)
![]() ;
;
(5.25)
для параболы
второго порядка:
![]()
![]() ;
;
![]() ; (5.26)
; (5.26)
![]() ; (5.27)
; (5.27)
![]() . (5.28)
. (5.28)
В случае, если
основные признаки (характер динамики
развития) типовых моделей не выражаются
явно, необходимо просчитать несколько
моделей и выбрать из них адекватную.
Адекватность определяется по значению
стандартизированной ошибки аппроксимации
 , (5.29)
, (5.29)
где
![]() – значение уровняi–того
– значение уровняi–того
года (данные в задании),
![]() ,
,
– значение уровня i–того
года, полученное по математической
модели.
Суммирование
производится по заданным исходным
данным по nгодам.
Адекватной считается та модель, для
которой![]() минимальна.
минимальна.
Подробнее
расчеты по построению математических
моделей тренда рассмотрены в [17].
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Темп роста – это прирост какой-либо изучаемой величины за один временной период (обычно применяется к году).
Темп прироста – это прирост какой либо изучаемой величины за один временной период за вычетом 100%.
Темп роста и темп прироста измеряются в процентах и являются относительными величинами. Темп роста – всегда величина положительная, темп прироста может быть отрицательным. Темп прироста равен темп роста минус 100%.
Теперь рассмотрим расчет темпа роста и темпа прироста более подробно.
Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ
Расчет темпа роста и прироста
Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: темп роста и темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов – формулы расчета темпа роста и прироста.
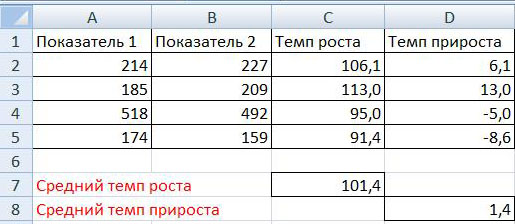
На рисунке представлен пример расчета темпа роста и прироста:
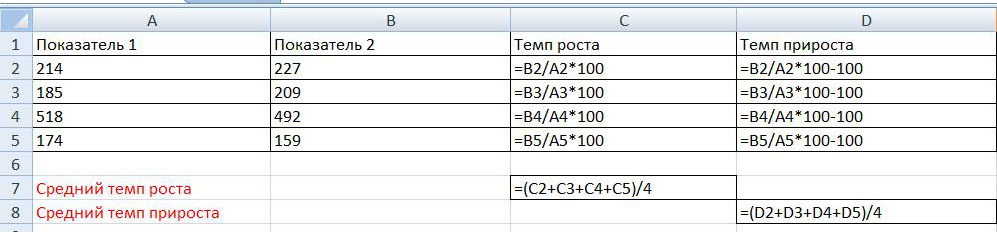
Для наглядности на рисунке ниже приведен этот же пример, только с открытыми формулами:
На рисунке видно, что определение темпа роста осуществляется путем деления Показателя 2 на Показатель 1 и умножения на 100%. При этом темп прироста равен: деление показателя 2 на показатель 1 умножение на 100% и минус 100%, то есть темп прироста равен темп роста минус 100%.
Расчет средних темпов роста и прироста
Так же на рисунках указано как рассчитывается средний темп роста и средний темп прироста. Для определения среднего темпа роста необходимо сложить показатели за все четыре периоды и разделить полученную сумму на количество периодов, то есть на 4. Аналогично рассчитывается средний темп прироста – сумма темпов прироста за все периоды делится на количество периодов.
Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ
Расчет базисного темпа роста и базисного темпа прироста
Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов – формулы расчета темпа роста и прироста.
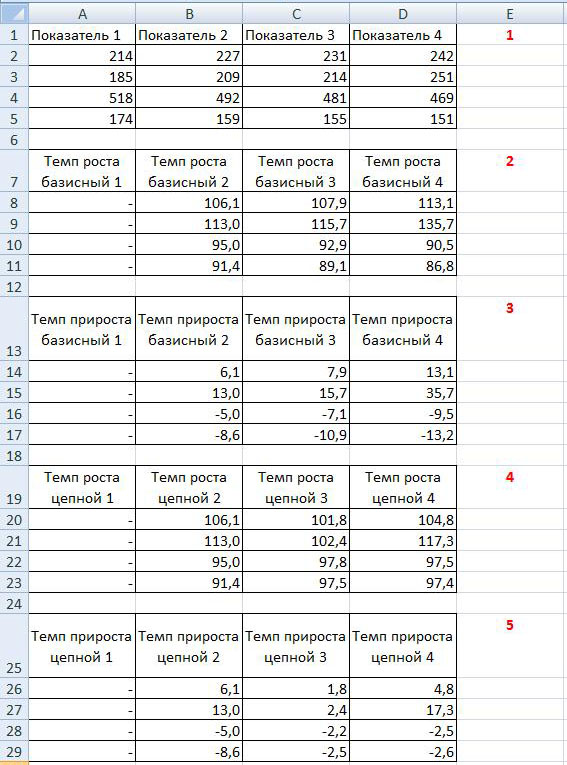
На рисунке ниже представлен расчет базисного темпа роста и прироста (таблицы 2 и 3):
Расчет базисного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя.
Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ
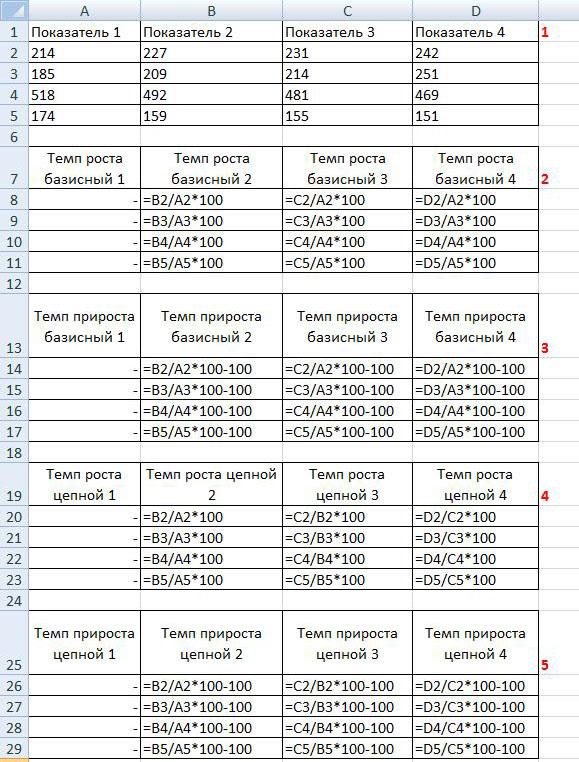
В примере за базисный показатель принят Показатель 1, поэтому базисный темп роста или базисный темп прироста рассчитывается исходя из этого положения, то есть при расчете базисного темпа роста Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, при расчете базисного темпа прироста из каждого показателя базисного темпа роста вычитаем 100.
Расчет цепного темпа роста и цепного темпа прироста
На рисунке выше представлен расчет базисного темпа роста и прироста (таблицы 4 и 5).
Расчет цепного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя. В отличие от базисного темпа роста или прироста, цепной темп роста или прироста рассчитывается из текущего и предыдущего показателя.
То есть цепной темп роста или цепной темп прироста рассчитывается следующим образом: Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 2 и умножаем на 100, далее Показатель 4 делим на Показатель 3 и умножаем на 100, при расчете цепного темпа прироста из каждого показателя цепного темпа роста вычитаем 100.
Для того, чтобы закрепить полученную информацию, обратите внимание на рисунок ниже, в котором отражены формулы расчета: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста:
Обратите внимание, что при расчете базисного и цепного показателей, значения базисного и цепного темпов роста и прироста равны, так как при избрании в качестве базисного показателя первого из ряда, они рассчитываются одинаково.
Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ
3.1. Понятие выборки (применительно к исследованию в психологии)
3.2. Не любите проводить социологическое исследование? Вы просто не умеете его готовить!
3.3. Корреляционный анализ по методу Спирмена (ранги Спирмена)
3.4. Дискуссия: Объект и Предмет исследования или наоборот?
3.5. Решение задач по праву. Как решить задачу по Юриспруденции?
3.6. Как рассчитать темп роста и прироста?
3.7. Как выбрать тему дипломной работы?
3.8. Методы исследования в дипломе, пример