МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Государственное высшее учебное заведение «ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра физики
ОТЧЕТ по лабораторной работе №85
ЗНАКОМСТВО С РАБОТОЙ САХАРИМЕТРА. ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ САХАРНЫХ РАСТВОРОВ
Выполнил студент группы_________________
________________________________________
Преподаватель кафедры физики
________________________________________
Отметка о защите_________________________
2014
a lc ,
|
Волков А.Ф., Лумпиева Т.П. |
Физический практикум |
Лабораторная работа №85
ЗНАКОМСТВО С РАБОТОЙ САХАРИМЕТРА. ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ САХАРНЫХ РАСТВОРОВ
Цель работы ознакомиться с работой сахариметра, определить концентрацию растворов сахара.
Приборы и принадлежности: сахариметр, трубки с раствором сахара. Общие положения
Электромагнитные волны являются поперечными. Это означает, что вектор напряженности электрического поля E и вектор напряженности магнитно-
го поля H располагаются в плоскости, перпендикулярной направлению распространения волны. Физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями вектора напряженности элек-
трического поля E . Поэтому его называют световым вектором. Направление колебаний светового вектора с течением времени может меняться. Если все направления колебаний светового вектора в плоскости, перпендикулярной направлению распространения волны, равновероятны, то свет называют есте-
ственным.
Свет, в котором направления колебаний упорядочены каким-либо образом, называется поляризованным. Если колебания светового вектора происходят только в одной проходящей через луч плоскости, то свет называется плоско (или линейно) поляризованным. Явлением поляризации называется выделение поляризованного света из естественного.
При прохождении поляризованного света через некоторые вещества происходит поворот плоскости поляризации световой волны. Это явление называется вращением плоскости поляризации. Вещества, которые способны поворачивать плоскость поляризации падающих на них волн, называются оптически активными. Оптически активными могут быть как кристаллы, так и жидкости. Например, кварц, раствор сахара, глюкозы. Различают правое вращение, или положительное и левое, или отрицательное. При правом вращении плоскость поляризации поворачивается по часовой стрелке для луча, падающего в глаз
наблюдателя, при левом – в противоположном направлении.
Для оптически активных жидкостей угол поворота плоскости поляризации определяется соотношением:
(1)
где l – толщина слоя;
c – концентрация раствора;
a – удельная постоянная вращения, зависящая от природы вещества.
Измерение угла поворота плоскости поляризации производят с помощью прибора, который называется поляриметром. Если его шкала проградуирована в соответствии с концентрацией раствора сахара, то такой поляриметр называется сахариметром. Зная угол поворота плоскости поляризации, можно рассчитать концентрацию раствора:
1

|
Волков А.Ф., Лумпиева Т.П. |
Физический практикум |
||
|
c |
|||
|
. |
(2) |
||
|
a l |
Описание установки
В данной работе используется универсальный сахариметр СУ-4. Принцип работы сахариметра состоит в следующем. Свет от источника проходит сначала через поляризатор и поляризуется. Затем его пропускают через полутеневую пластину, которая разделяет свет на две половины так, что плоскость поляризации обеих половин светового пучка составит одинаковый угол с плоскостью пропускания анализатора, расположенного после пластины. При этом в окуляре видны два поля сравнения одинаковой яркости, разделенные тонкой линией (рис. 1а).
Если в кюветное отделение между поляризатором и анализатором поместить трубку с раствором сахара, то раствор повернет плоскость поляризации.
|
Равенство |
полей |
сравнения |
||
|
нарушится (рис. 1б, в). Уравни- |
||||
|
вая яркость полей сравнения, |
||||
|
производят отсчет по нониусу |
||||
|
шкалы, которую |
наблюдают |
|||
|
через верхний окуляр. Поля |
||||
|
сравнения |
наблюдают через |
|||
|
Рисунок 1 |
нижний окуляр. |
|||
|
В сахариметре применена |
||||
международная сахарная шкала. 100 S соответствуют 34,62 угловым. Цена деления основной шкалы 1 S, цена деления нониуса 0,05 S. Установка нуля нониуса показана на рис. 2.
|
0.05oS |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
100 75 |
50 |
25 _ 0+ |
25 |
50 |
75 100 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
40 |
20 |
10 |
_ 0+ |
10 |
20 |
30 |
130 |
Рисунок 2 На рис. 3 показано положение нониуса и шкалы, соответствующее отсчету
|
0.05oS |
«+11,55 S» (нуль нониуса расположен правее |
||||||||||||||||||||||||||||||||||||||||
|
100 |
75 |
50 |
25 |
_ 0+ |
25 |
50 |
75 |
100 |
нуля шкалы на11 полных делений и вправой |
||||||||||||||||||||||||||||||||
|
части нониуса с одним из делений шкалы |
|||||||||||||||||||||||||||||||||||||||||
|
10 |
_0+ |
10 |
20 |
30 |
совмещаетсяегоодиннадцатоеделение). |
||||||||||||||||||||||||||||||||||||
|
Рисунок 3 |
На рис. 4 показано положение нони- |
||||||||||||||||||||||||||||||||||||||||
|
0.05oS |
уса и шкалы, соответствующее отсчету |
||||||||||||||||||||||||||||||||||||||||
|
100 |
75 |
50 |
25 |
_ 0+ |
25 |
50 |
75 |
100 |
« 3,25 S» (нуль нониуса расположен левее |
||||||||||||||||||||||||||||||||
|
нуля шкалы на три полных деления и в ле- |
|||||||||||||||||||||||||||||||||||||||||
|
вой части нониуса с одним из делений |
|||||||||||||||||||||||||||||||||||||||||
|
20 |
10 |
_ 0+ |
10 |
20 |
|||||||||||||||||||||||||||||||||||||
|
Рисунок 4 |
шкалы совмещается его пятое деление). |
||||||||||||||||||||||||||||||||||||||||
2
|
Волков А.Ф., Лумпиева Т.П. |
Физический практикум |
Подготовка к работе
(ответы представить в письменном виде)
1.Какова цель работы?
2.Какие величины Вы будете измерять непосредственно?
3.Запишите формулу, по которой Вы будете рассчитывать постоянную вращения сахариметра. Поясните смысл обозначений.
4.Запишите формулу, по которой Вы будете рассчитывать концентрацию растворов. Поясните смысл обозначений.
Выполнение работы
1.Включить шнур электропитания в сеть.
2.Включить кнопкой осветитель и установить рукой резистора такую яркость полей, при которой наиболее четко воспринимается зрением разница яркости полей сравнения.
3.Проверить установку нуля. Для этого надо закрыть крышку кюветного отделения без установки в нем кюветы. Уравнять яркость полей сравнения вращением ручки компенсатора, который находится под нижним окуляром. Нулевое деление нониуса должно совместится с нулевым делением шкалы (см. рис. 2). Если нулевой отсчет отличается от нуля не более чем на одно деление нониуса, нуль считается установленным правильно.
4.Поместить в кюветное отделение в трубку с раствором известной концен-
трации (с0 = 26%). Длина трубки l0 = 10 cм. Вращая ее вокруг своей оси или перемещая по кюветному отделению, найти такое положение, при котором линия раздела полей сравнения делит поле зрения на две равные части. Поля сравнения при этом имеют разную яркость (см. рис. 1б, в).
5.Вращая ручку компенсатора, уравнять поля сравнения (см. рис 1а) и снять отсчет по шкале.
6.Повторить опыт с раствором известной концентрации еще два раза согласно пункту 5. Перед началом каждого опыта нуль шкалы совмещать с нулем нониуса.
7.Аналогичные измерения провести для двух трубок с растворами неизвестной концентрации. Длина трубок l = 20 cм.
3
|
Волков А.Ф., Лумпиева Т.П. |
Физический практикум |
Оформление отчета
1.Расчеты
1.Найти среднее значение угла поворота плоскости поляризации раствором известной концентрации.
2.По найденному среднему значению угла поворота, известной длине трубки l0
иизвестной концентрации с0, рассчитать постоянную вращения а :
|
a |
ср |
. |
(3) |
|
c0 l0 |
3.Рассчитать по формуле (2) концентрацию раствора в первой трубке по результатам каждого опыта. Найти среднее значение концентрации.
4.Рассчитать по формуле (2) концентрацию раствора во второй трубке по результатам каждого опыта. Найти среднее значение концентрации.
5.Рассчитать абсолютную погрешность как для прямых измерений для каждой концентрации.
6.Найти относительную погрешность измерений каждого опыта. Записать окончательные результаты в стандартном виде:
cc с
2.Защита работы
(ответы представить в письменном виде)
1.Какое явление изучалось в данной работе? В чем оно заключается?
2.С каким свойством электромагнитных волн связано явление поляризации?
3.Почему вектор напряженности электрического поля называют световым вектором?
4.Какие вещества называются оптически активными? Приведите примеры оптически активных веществ.
5.От чего зависит угол поворота плоскости поляризации?
6.Каково назначение сахариметра?
4

|
Волков А.Ф., Лумпиева Т.П. |
Физический практикум |
|||||||
|
ПРОТОКОЛ |
||||||||
|
измерений к лабораторной работе № 85 |
||||||||
|
Выполнил(а)_____________________ |
Группа__________________ |
|||||||
|
Таблица 1 |
||||||||
|
c0, |
||||||||
|
№ |
l0, |
, |
||||||
|
п/п |
см |
% |
S |
|||||
|
1 |
||||||||
|
2 |
||||||||
|
3 |
||||||||
|
среднее |
||||||||
|
Таблица 2 |
||||||||
|
, |
||||||||
|
№ |
l, |
c, |
||||||
|
п/п |
см |
S |
% |
|||||
|
1 |
||||||||
|
2 |
||||||||
|
3 |
||||||||
|
среднее |
||||||||
|
Таблица 3 |
||||||||
|
, |
||||||||
|
№ |
l, |
c, |
||||||
|
п/п |
см |
S |
% |
|||||
|
1 |
||||||||
|
2 |
||||||||
|
3 |
||||||||
|
среднее |
|
Дата________ |
Подпись преподавателя___________________ |
5
Усреднение углов… Опять
Я хочу вычислить среднее значение из набора углов, который представляет исходный азимут (от 0 до 360 градусов) – (аналогично направлению ветра)
Я знаю, что это обсуждалось ранее (несколько раз). Принятым ответом было вычислить единичные векторы по углам и взять угол их среднего.
Однако этот ответ определяет среднее не интуитивным способом. Среднее значение 0, 0 и 90 будет atan( (sin(0)+sin(0)+sin(90)) / (cos(0)+cos(0)+cos(90))) = atan(1/2)= 26,56 град
Я ожидаю, что среднее значение 0, 0 и 90 будет 30 градусов.
Поэтому я думаю, что было бы справедливо задать вопрос еще раз: как бы вы рассчитали среднее значение, поэтому такие примеры дадут интуитивный ожидаемый ответ.
Изменить 2014:
Задав этот вопрос, я разместил статью о CodeProject, в которой предлагается тщательный анализ. В статье рассматриваются следующие справочные задачи:
- Приведенное время суток [00:00-24:00) для каждого рождения, произошедшего в США в 2000 году. Рассчитать среднее время рождения при рождении.
- При наличии множества измерений направления от стационарного передатчика к стационарному приемнику с использованием методики измерения с обернутой нормальной распределенной ошибкой – оцените направление.
- Учитывая мультимножество оценок азимута между двумя точками, сделанных “обычными” людьми (при условии, что они подверглись усеченной усеченной нормальной распределенной ошибке) – Оцените направление.
2009-11-28 19:19
11
ответов
Решение
Спасибо всем за то, что помогли мне увидеть мою проблему более четко.
Я нашел то, что искал. Это называется метод Мицуты.
Входы и выходы находятся в диапазоне [0..360).
Этот метод хорош для усреднения данных, которые были отобраны с использованием постоянных интервалов выборки.
В этом методе предполагается, что разница между последовательными выборками составляет менее 180 градусов (что означает, что если мы не будем производить выборку достаточно быстро, изменение дискретизированного сигнала на 330 градусов будет неправильно определено как изменение на 30 градусов в другом направлении и будет вставить ошибку в расчет). Теорема отсчетов Найквиста – Шеннона?
Вот код C++:
double AngAvrg(const vector<double>& Ang)
{
vector<double>::const_iterator iter= Ang.begin();
double fD = *iter;
double fSigD= *iter;
while (++iter != Ang.end())
{
double fDelta= *iter - fD;
if (fDelta < -180.) fD+= fDelta + 360.;
else if (fDelta > 180.) fD+= fDelta - 360.;
else fD+= fDelta ;
fSigD+= fD;
}
double fAvrg= fSigD / Ang.size();
if (fAvrg >= 360.) return fAvrg -360.;
if (fAvrg < 0. ) return fAvrg +360.;
return fAvrg ;
}
Это объясняется на странице 51 по адресу http://www.epa.gov/scram001/guidance/met/mmgrma.pdf
Спасибо Маре за отправку ссылки в качестве комментария.
Если данные выборки являются постоянными, но наше устройство для выборки имеет неточность с распределением фон Мизеса, будет уместным вычисление единичных векторов.
2009-12-01 19:11
[Обратите внимание, что вопрос ОП (но не заголовок), по-видимому, изменился на довольно специализированный вопрос (“… среднее ПОСЛЕДОВАТЕЛЬНОСТИ углов, где каждое последующее сложение не отличается от скользящего среднего более чем на определенную величину”.) – см. @MaR комментарий и мой.Мой следующий ответ касается названия ОП и основной части обсуждения и ответов, связанных с ним.]
Это не вопрос логики или интуиции, а определения. Это обсуждалось на SO раньше без какого-либо реального консенсуса. Углы должны быть определены в пределах диапазона (который может быть от -PI до +PI, или от 0 до 2*PI или может быть от -Inf до +Inf. Ответы будут разными в каждом случае.
Мир “угол” вызывает путаницу, поскольку это означает разные вещи. Угол зрения представляет собой величину без знака (и обычно это PI > theta > 0. В этом случае могут быть полезны “нормальные” средние значения. Угол поворота(например, общее вращение, если фигуристка) может или не может быть подписан и может включать в себя тета> 2* пи и тета <-2 * пи.
Здесь определяетсяугол = направление, для которого требуются векторы. Если вы используете слово “направление” вместо “угол”, вы поймете намерение ОП (кажущийся оригинальным), и это поможет отойти от скалярных величин.
Википедия показывает правильный подход, когда углы определяются кругово, так что
theta = theta+2*PI*N = theta-2*PI*N
Ответом для среднего является НЕ скаляр, а вектор. ОП может не чувствовать, что это интуитивно понятно, но это единственный полезный правильный подход. Мы не можем переопределить квадратный корень из -4, чтобы он был равен -2, потому что это более наглядно – это должно быть +-2*i. Точно так же среднее значение подшипников -90 градусов и +90 градусов – это вектор нулевой длины, а не 0,0 градусов.
Википедия ( http://en.wikipedia.org/wiki/Mean_of_circular_quantities) имеет специальный раздел и состояния (Уравнения LaTeX и их можно увидеть в Википедии):
Большинство обычных средних значений терпят неудачу на круглых величинах, таких как углы, дневное время, дробные части действительных чисел. Для этих величин вам нужно среднее значение круговых величин.
Поскольку среднее арифметическое не является эффективным для углов, можно использовать следующий метод для получения как среднего значения, так и показателя дисперсии углов:
Переведите все углы в соответствующие точки на единичной окружности, например, α в (cosα,sinα). То есть конвертировать полярные координаты в декартовы. Затем вычислите среднее арифметическое этих точек. Полученная точка будет лежать на диске устройства. Переведите эту точку обратно в полярные координаты. Угол является разумным средним из входных углов. Результирующий радиус будет 1, если все углы равны. Если углы равномерно распределены по окружности, то результирующий радиус будет равен 0, а круговое среднее отсутствует. Другими словами, радиус измеряет концентрацию углов.
Учитывая углы alpha_1,dots,alpha_n, среднее значение вычисляется как
M alpha = operatorname{atan2}left(frac{1}{n}cdotsum_{j=1}^nsinalpha_j,
frac{1}{n}cdotsum_{j=1}^n
cosalpha_jright)используя вариант функции арктангенса atan2, или
M alpha = argleft(frac{1}{n}cdotsum_{j=1}^nЕхр ( CDOT alpha_j) справа)
используя комплексные числа.
Обратите внимание, что в вопросе OP угол 0 является чисто произвольным – нет ничего особенного в том, что ветер приходит от 0, а не к 180 (за исключением того, что в этом полушарии на велосипеде холоднее). Попробуйте изменить 0,0,90 на 289, 289, 379 и посмотрите, как простая арифметика больше не работает.
(Есть некоторые распределения, где углы 0 и PI имеют особое значение, но они здесь не входят в объем).
Вот некоторые интенсивные предыдущие обсуждения, которые отражают текущее распространение взглядов:-)
http://mathforum.org/library/drmath/view/53924.html
Как вы рассчитываете среднее значение для набора циклических данных?
http://forums.xkcd.com/viewtopic.php?f=17&t=22435
http://www.allegro.cc/forums/thread/595008
2009-11-28 21:15
Что это вообще значит для среднего источника подшипников? Начните с ответа на этот вопрос, и вы приблизитесь к тому, чтобы определить, что вы подразумеваете под средним углом.
На мой взгляд, угол с касательной, равной 1/2, является правильным ответом. Если у меня есть единичная сила, толкающая меня в направлении вектора (1, 0), другая сила, толкающая меня в направлении вектора (1, 0), и третья сила, толкающая меня в направлении вектора (0, 1).), то результирующая сила (сумма этих сил) – это сила, толкающая меня в направлении (1, 2). Это векторы, представляющие подшипники 0 градусов, 0 градусов и 90 градусов. Угол, представленный вектором (1, 2), имеет касательную, равную 1/2.
Отвечая на ваше второе редактирование:
Допустим, мы измеряем направление ветра. Наши 3 измерения были 0, 0 и 90 градусов. Поскольку все измерения одинаково надежны, почему наша лучшая оценка направления ветра не должна составлять 30 градусов? установка его на 25,56 градусов – это смещение в сторону 0…
Хорошо, вот проблема. Единичный вектор с углом 0 не обладает такими же математическими свойствами, как действительное число 0. Использование обозначений 0v чтобы представить вектор с углом 0, обратите внимание, что
0v + 0v = 0v
ложно, но
0 + 0 = 0
верно для реальных чисел. Так что если 0v представляет ветер с единичной скоростью и углом 0, то 0v + 0v ветер с удвоенной единицей скорости и углом 0. А потом, если у нас есть третий вектор ветра (который я буду представлять с помощью обозначения 90v), который имеет угол 90 и единичную скорость, то ветер, возникающий из суммы этих векторов, имеет уклон, потому что он движется с удвоенной частотой вращения в горизонтальном направлении, но только с единичной скоростью в вертикальном направлении.
user45914
29 ноя ’09 в 18:08
2009-11-29 18:08
2009-11-29 18:08
Это неверно на каждом уровне.
Векторы добавляются в соответствии с правилами сложения векторов. “Интуитивный, ожидаемый” ответ может быть не таким интуитивным.
Возьмите следующий пример. Если у меня есть один единичный вектор (1, 0) с источником в (0,0), который указывает в направлении +x, и другой (-1, 0), который также имеет начало в (0,0), который указывает в -x-направление, каким должен быть “средний” угол?
Если я просто добавлю углы и разделю на два, я могу утверждать, что “среднее” составляет либо +90, либо -90. Как вы думаете, какой из них должен быть?
Если я добавлю векторы в соответствии с правилами сложения векторов (компонент за компонентом), я получу следующее:
(1, 0) + (-1, 0) = (0, 0)
В полярных координатах это вектор с нулевой величиной и нулевым углом.
Так каким должен быть “средний” угол? У меня есть три разных ответа для простого случая.
Я думаю, что ответ заключается в том, что векторы не подчиняются той же интуиции, что и числа, потому что они имеют величину и направление. Может быть, вам лучше описать, какую проблему вы решаете.
Какое бы решение вы ни выбрали, я бы посоветовал вам основывать его на векторах. Так будет всегда правильно.
user37213
28 ноя ’09 в 19:33
2009-11-28 19:33
2009-11-28 19:33
Изменить: Эквивалентный, но более надежный алгоритм (и более простой):
- разделить углы на 2 группы, [0-180) и [180-360)
- численно среднее значение обеих групп
- усредните 2 средних по группе с правильным взвешиванием
- если произошло завертывание, исправить на 180˚
Это работает, потому что усреднение чисел работает “логически”, если все углы находятся в одном и том же полукруге. Затем мы откладываем получение ошибки обтекания до самого последнего шага, где ее легко обнаружить и исправить. Я также добавил некоторый код для обработки случаев с противоположными углами. Если средние значения противоположны, мы отдаем предпочтение полусфере, в которой было больше углов, а в случае равных углов в обоих полушариях мы возвращаемся None потому что никакой средний не будет иметь смысла.
Новый код:
def averageAngles2(angles):
newAngles = [a % 360 for a in angles];
smallAngles = []
largeAngles = []
# split the angles into 2 groups: [0-180) and [180-360)
for angle in newAngles:
if angle < 180:
smallAngles.append(angle)
else:
largeAngles.append(angle)
smallCount = len(smallAngles)
largeCount = len(largeAngles)
#averaging each of the groups will work with standard averages
smallAverage = sum(smallAngles) / float(smallCount) if smallCount else 0
largeAverage = sum(largeAngles) / float(largeCount) if largeCount else 0
if smallCount == 0:
return largeAverage
if largeCount == 0:
return smallAverage
average = (smallAverage * smallCount + largeAverage * largeCount) /
float(smallCount + largeCount)
if largeAverage < smallAverage + 180:
# average will not hit wraparound
return average
elif largeAverage > smallAverage + 180:
# average will hit wraparound, so will be off by 180 degrees
return (average + 180) % 360
else:
# opposite angles: return whichever has more weight
if smallCount > largeCount:
return smallAverage
elif smallCount < largeCount:
return largeAverage
else:
return None
>>> averageAngles2([0, 0, 90])
30.0
>>> averageAngles2([30, 350])
10.0
>>> averageAngles2([0, 200])
280.0
Вот немного наивный алгоритм:
- убрать все углы откоса из списка
- взять пару углов
- поверните их в первый и второй квадрант и усредните их
- повернуть средний угол назад на ту же величину
- для каждого оставшегося угла усредните таким же образом, но с последовательно увеличивающимся весом до составного угла
некоторый код на Python (шаг 1 не реализован)
def averageAngles(angles):
newAngles = [a % 360 for a in angles];
average = 0
weight = 0
for ang in newAngles:
theta = 0
if 0 < ang - average <= 180:
theta = 180 - ang
else:
theta = 180 - average
r_ang = (ang + theta) % 360
r_avg = (average + theta) % 360
average = ((r_avg * weight + r_ang) / float(weight + 1) - theta) % 360
weight += 1
return average
user73681
28 ноя ’09 в 19:35
2009-11-28 19:35
2009-11-28 19:35
Вот ответ, который я дал на этот же вопрос:
Как вы рассчитываете среднее значение для набора циклических данных?
Это дает ответы в соответствии с тем, что ОП говорит, что он хочет, но внимание должно быть уделено этому:
“Я также хотел бы подчеркнуть, что хотя это истинное среднее углов, в отличие от векторных решений, это не обязательно означает, что это решение, которое вы должны использовать, среднее значение соответствующих единичных векторов вполне может быть значением, которое вы на самом деле следует использовать “.
2010-09-06 13:52
На мой взгляд, речь идет об углах, а не векторах. По этой причине среднее значение 360 и 0 действительно равно 180. Среднее значение за один оборот и без поворотов должно быть половиной оборота.
2009-11-28 19:38
Возможно, вы могли бы представить углы как кватернионы и взять среднее значение этих кватернионов и преобразовать их обратно в угол.
Я не знаю, дает ли это вам то, что вы хотите, потому что кватернионы – это скорее вращения, чем углы. Я также не знаю, даст ли это вам что-то отличное от векторного решения.
Кватернионы в 2D упрощаются до комплексных чисел, так что я думаю, что это просто векторы, но, возможно, какой-нибудь интересный алгоритм усреднения кватернионов, например http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20070017872_2007014421.pdf при упрощении до 2D будет вести себя лучше, чем просто векторное среднее.
2009-12-01 21:19
Вы можете сделать это: скажем, у вас есть набор углов в массиве angleЗатем для вычисления массива сначала выполните: angle[i] = angle[i] mod 360Теперь выполните простое среднее по массиву. Поэтому, когда у вас есть 360, 10, 20, вы в среднем 0, 10 и 20 – результаты интуитивно понятны.
2009-11-28 19:34
Ну вот! Ссылка https://www.wxforum.net/index.php?topic=8660.0
def avgWind(directions):
sinSum = 0
cosSum = 0
d2r = math.pi/180 #degree to radian
r2d = 180/math.pi
for i in range(len(directions)):
sinSum += math.sin(directions[i]*d2r)
cosSum += math.cos(directions[i]*d2r)
return ((r2d*(math.atan2(sinSum, cosSum)) + 360) % 360)
a= np.random.randint(low=0, high=360, size=6)
print(a)
avgWind(a)
2020-11-06 07:08
Что плохого в том, чтобы принимать набор углов в качестве реальных значений и просто вычислять среднее арифметическое этих чисел? Тогда вы получите интуитивный (0+0+90)/3 = 30 градусов.
Редактировать: Спасибо за полезные комментарии и указание, что углы могут превышать 360. Я считаю, что ответом может быть обычное среднее арифметическое значение, уменьшенное по модулю 360: мы суммируем все значения, делим на количество углов и затем вычитаем / добавляем кратное 360, так что результат лежит в интервале [0..360).
2009-11-28 19:24
Я думаю, что проблема связана с тем, как вы относитесь к углам больше 180 (и к углам больше 360). Если вы уменьшите углы до диапазона от +180 до -180, прежде чем добавить их к общему значению, вы получите нечто более разумное:
int AverageOfAngles(int angles[], int count)
{
int total = 0;
for (int index = 0; index < count; index++)
{
int angle = angles[index] % 360;
if (angle > 180) { angle -= 360; }
total += angle;
}
return (int)((float)total/count);
}
user33686
28 ноя ’09 в 19:41
2009-11-28 19:41
2009-11-28 19:41
First, SO(3) of course has its unique invariant probabilistic measure. Hence, “random rotation” is a well-defined SO(3)-valued random variable. Each rotation (an element of SO(3)) has an uniquely defined rotation angle θ, from 0 to 180° (π) because of axis–angle representation. (Note that axis is undefined for θ = 0 and has two possible values for θ = 180°, but θ itself has no ambiguity.) Hence, “angle of a random rotation” is a well-defined random angle.
Why is its average closer to one end (180°) than to another (0)? In short, because there are many 180° rotations, whereas rotation by zero angle is unique (identity map).
Note that I ignore Spin(3) → SO(3) covering that is important in quaternionic discourse, but it won’t change the result: Haar measure on Spin(3) projected onto SO(3) gives the same Haar measure on SO(3), hence there is no difference whether do we make computations on S3 of unit quaternions (the same as Spin(3)) or directly on SO(3).
В математике и статистике , А круглое среднее или угловое среднее является средним предназначен для углов и аналогичных циклических величин, таких как daytimes и дробные части из действительных чисел . Это необходимо, поскольку большинство обычных средств может не подходить для угловых величин. Например, среднее арифметическое 0 ° и 360 ° равно 180 °, что вводит в заблуждение, поскольку 360 ° равняется 0 ° по модулю полного цикла. В качестве другого примера, «среднее время» между 23:00 и 1:00 – это либо полночь, либо полдень, в зависимости от того, являются ли эти два времени частью одной ночи или частью одного календарного дня. Круговое среднее – один из простейших примеров круговой статистики и статистики неевклидовых пространств .
Определение
Поскольку среднее арифметическое не всегда подходит для углов, можно использовать следующий метод для получения как среднего значения, так и измерения дисперсии углов:
Преобразуйте все углы в соответствующие точки на единичной окружности , например, в . То есть преобразовать полярные координаты в декартовы координаты . Затем вычислите среднее арифметическое этих точек. Полученная точка будет находиться внутри единичного диска. Преобразуйте эту точку обратно в полярные координаты. Угол – это разумное среднее значение входных углов. Результирующий радиус будет равен 1, если все углы равны. Если углы равномерно распределены по окружности, то результирующий радиус будет равен 0, а среднего кругового нет. (На самом деле невозможно определить непрерывную операцию среднего на окружности.) Другими словами, радиус измеряет концентрацию углов.
Учитывая углы, общая формула среднего с использованием варианта atan2 функции арктангенса имеет вид
или, используя комплексные числа :
Чтобы сопоставить приведенный выше вывод с использованием среднего арифметического баллов, суммы необходимо разделить на . Однако, масштабирование не имеет значения , и , таким образом , он может быть опущен.
Это вычисление дает результат, отличный от среднего арифметического, причем разница больше, когда углы широко распределены. Например, среднее арифметическое трех углов 0 °, 0 ° и 90 ° составляет (0 + 0 + 90) / 3 = 30 °, но среднее арифметическое значение равно 26,565 °. Более того, с помощью среднего арифметического круговая дисперсия определяется только ± 180 °.
Характеристики
Круговое среднее 
- максимизирует вероятность среднего параметра распределения фон Мизеса и
- минимизирует сумму определенного расстояния по окружности, точнее
- Расстояние равно половине квадрата евклидова расстояния между двумя точками единичной окружности, связанной с и .
Пример
Простой способ вычислить среднее значение ряда углов (в интервале [0 °, 360 °)) – вычислить среднее значение косинусов и синусов каждого угла и получить угол путем вычисления арктангенса. В качестве примера рассмотрим следующие три угла: 10, 20 и 30 градусов. Интуитивно, вычисление среднего значения потребовало бы сложения этих трех углов вместе и деления на 3, что в данном случае действительно привело бы к правильному среднему углу, равному 20 градусам. При повороте этой системы против часовой стрелки на 15 градусов три угла становятся 355 градусов, 5 градусов и 15 градусов. Наивное среднее значение теперь составляет 125 градусов, что является неправильным ответом, поскольку должно быть 5 градусов. Среднее векторное можно вычислить следующим образом, используя средний синус и средний косинус :
Это можно выразить более лаконично, если учесть, что данные направления на самом деле являются векторами единичной длины. В случае одномерных данных эти точки данных могут быть удобно представлены в виде комплексных чисел единичной величины , где – измеренный угол. Тогда средний результирующий вектор для выборки будет:
Тогда выборочный средний угол является аргументом среднего результирующего:
Длина результирующего вектора выборочного среднего равна:
и будет иметь значение от 0 до 1. Таким образом, результирующий вектор выборочного среднего может быть представлен как:
Подобные вычисления также используются для определения круговой дисперсии .
Смотрите также
- Круговое распределение
- Круговое стандартное отклонение
- Направленная статистика
- Центроид
- Центр массы
использованная литература
-
^ Кристофер М. Бишоп: Распознавание образов и машинное обучение (информатика и статистика) ,
ISBN 0-387-31073-8
дальнейшее чтение
Джаммаламадака, С. Рао и СенГупта, А. (2001). Темы циркулярной статистики , раздел 1.3, World Scientific Press, Сингапур. ISBN 981-02-3778-2
внешние ссылки
- Математика и статистика круговых значений с помощью инфраструктуры C ++ 11 , C ++ 11 для круговых значений (углов, времени суток и т. Д.), Математики и статистики
3.1 Теоретические основы и методика метрологических испытаний лаборатории в плане дороги
Проведение метрологических испытаний информационно-измерительного комплексам дорожной лаборатории требует разработки теоретических основ и методики их выполнения.
В качестве основного метода исследования точности принят метод сравнения результатов, полученных с его помощью, с аналогичными результатами, полученными на основе геодезических измерений. При этом геодезические данные приняты за основные, поскольку они обладают наиболее высокой точностью. Вместе с тем исследование точности дорожной лаборатории путём сравнения результатов, вычисленных при разном числе наблюдений (проездов лаборатории) также позволяет получать ряд ценных выводов, основанных на внутренней сходимости этих данных.
Решение задачи рассмотрим раздельно в плане и в продольном профиле.
Чтобы можно использовать ходовую лабораторию для съёмки плана автомобильной дороги значительной протяжённости необходимо выполнение двух условий:
1. Лаборатория должна обеспечивать измерение азимутов направлений или углов поворота оси дороги с достаточно высокой точностью (порядка нескольких угловых минут);
2. Лаборатория должна обеспечивать измерение расстояния с точностью не ниже 1/5000.
Например, при измерении азимутов или углов поворота с погрешностью ±10 и расстояний с относительной погрешностью =1/5000 положение точки в плане на оси дороги, имеющей не более одного угла поворота, через 10 км будет характеризоваться средней квадратической погрешностью, примерно равной
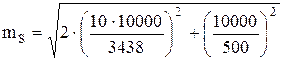 =45 м.
=45 м.
На планах масштаба 1:5000 этой величине соответствует 9 мм, а на планах масштаба 1:10000 – 5 мм. Эти погрешности, по-видимому, находятся на границе допустимых значений. Детальное рассмотрение вопроса о необходимой точности, которую должна обеспечивать лаборатория при съёмках автомобильных дорог в плане, может быть сделано в специальном исследовании.
Погрешность измерения азимутов или углов поворота с помощью дорожной лаборатории слагается из погрешностей отсчитывания по гирополукомпасу ( ![]() ) в начале и в конце закругления и погрешностей совмещения оси автомобиля лаборатории с осями прямолинейных участков дороги до начала и после конца закругления (
) в начале и в конце закругления и погрешностей совмещения оси автомобиля лаборатории с осями прямолинейных участков дороги до начала и после конца закругления (![]() ). Так как погрешности
). Так как погрешности ![]() и
и ![]() имеет случайный характер, то погрешность измерения углов поворота
имеет случайный характер, то погрешность измерения углов поворота ![]() будет равна
будет равна
![]() . (3.1)
. (3.1)
Погрешность отсчитывания по гирополукомпасу не превышает ±30. Погрешность же совмещения оси автомобиля с осями прямолинейных участков дороги до начала и после конца закругления может достигать нескольких градусов. Среднее квадратическое значение погрешности ![]() , а также закон распределения погрешностей совмещения оси автомобиля с осями прямолинейных участков дороги до начала и после конца закругления можно определить на основе следующих метрологических испытаний.
, а также закон распределения погрешностей совмещения оси автомобиля с осями прямолинейных участков дороги до начала и после конца закругления можно определить на основе следующих метрологических испытаний.
На закруглении автомобильной дороги определяют положение точек: НЗ (начало закругления) и КЗ (конец закругления). Наиболее точна задача решается геодезическим методом, описанным ниже. Автомобиль дорожной лаборатории подъезжает к точке НЗ со стороны прямолинейного участка дороги и водитель визуально совмещает его ось с осью прямолинейного участка дороги или линией, ей параллельной.
Запускают гироплукомпас и определяют: азимут начального направления ![]() . Дорожная лаборатория начинает движение по закруглению и заканчивает его за точкой КЗ на прямолинейном участке дороги. После остановки автомобиля по гирополукомпасу определяют азимут конечного направления его движения
. Дорожная лаборатория начинает движение по закруглению и заканчивает его за точкой КЗ на прямолинейном участке дороги. После остановки автомобиля по гирополукомпасу определяют азимут конечного направления его движения ![]() . Угол поворота оси дороги вычисляют по формуле
. Угол поворота оси дороги вычисляют по формуле
![]()
при правом угле поворота или по формуле
![]()
при левом угле поворота.
Далее водитель разворачивает автомобиль в обратном направлении и вновь повторяет весь путь, стараясь держать ось автомобиля до начала и после конца закругления по оси прямолинейных участков дороги. Описанные челночные проезды дорожной лаборатории по закруглению между точками НЗ и КЗ необходимо повторить примерно 25 раз, чтобы иметь достаточное число значения ![]() .
.
Статистическая обработка результатов испытаний состоит в следующем:
1. вычисляют среднее значение угла поворота ![]()
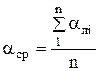 ;
;
2. Вычисляют среднюю квадратическую погрешность одного определения ![]()
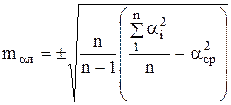 (3.2)
(3.2)
и среднего значения ![]()
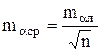 ; (3.3)
; (3.3)
3. Существуют основания полагать, что распределением величины ![]() и её погрешности
и её погрешности ![]() не противоречат нормальному закону (это утверждение можно проверить с помощью критериев согласия или другим простым методом).
не противоречат нормальному закону (это утверждение можно проверить с помощью критериев согласия или другим простым методом).
В связи с этим можно построить доверительные интервалы для истинного угла поворота ![]() по результатам одного i-го проезда лаборатория и по осредненным данным на n проездов:
по результатам одного i-го проезда лаборатория и по осредненным данным на n проездов:
![]() , (3.4)
, (3.4)
![]() , (3.5)
, (3.5)
где t – квантиль нормированного нормального распределения, соответствующий принятой вероятности ![]() .
.
Чтобы выяснить, насколько устойчиво значение ![]() при различном числе проездов лаборатории по закруглению, и как зависит погрешность
при различном числе проездов лаборатории по закруглению, и как зависит погрешность ![]() от числа проездов n, необходимо повторить все вычисления по
от числа проездов n, необходимо повторить все вычисления по ![]() проездов. Для этого все результаты необходимо разделить на четные и нечетные и вычислять все статистики отдельно по четным и нечетным значениям. Аналогично необходимо образовать выборки из 1,4,7,10,…, затем из 2,5,8,11,…и 3,6,9,12,…, значения
проездов. Для этого все результаты необходимо разделить на четные и нечетные и вычислять все статистики отдельно по четным и нечетным значениям. Аналогично необходимо образовать выборки из 1,4,7,10,…, затем из 2,5,8,11,…и 3,6,9,12,…, значения ![]() (то есть отобрать из всех значений каждый третий результат, начиная с первого, затем со второго и затем с третьего) и повторить трижды вычисления всех статистик по 1/3 всех проездов. Аналогичным образом необходимо образовать 4 выборки численностью
(то есть отобрать из всех значений каждый третий результат, начиная с первого, затем со второго и затем с третьего) и повторить трижды вычисления всех статистик по 1/3 всех проездов. Аналогичным образом необходимо образовать 4 выборки численностью ![]() и вновь повторить все вычисления.
и вновь повторить все вычисления.
Результаты всех вычислений можно представить на графиках. Если на графике провести горизонтальную прямую на уровне ![]() (
( ![]() – допустимое значение погрешности
– допустимое значение погрешности ![]() ), то на оси абсцисс можно получить значение n, которое обеспечивает определение
), то на оси абсцисс можно получить значение n, которое обеспечивает определение ![]() с допустимой погрешностью. Величина n определяет необходимое число челночных проездов дорожной лаборатории по закруглению, по данным которых определяют среднее значение угла поворота
с допустимой погрешностью. Величина n определяет необходимое число челночных проездов дорожной лаборатории по закруглению, по данным которых определяют среднее значение угла поворота ![]() с погрешностью, не более
с погрешностью, не более ![]() .
.
Из изложенного можно видеть, что основной погрешностью, определяющей точность измерения угла поворота ![]() с помощью дорожной лаборатории, является погрешность совмещения оси автомобиля (точнее, линии начального отсчёта гирополукомпаса) с осью прямолинейного участка дороги (или линией, ей параллельной), перед началом и после конца закругления дороги. Эта погрешность в несколько раз превосходит погрешность отсчитывания по гирополукомпасу, поэтому погрешность измерения угла поворота почти полностью определяется величиной погрешности
с помощью дорожной лаборатории, является погрешность совмещения оси автомобиля (точнее, линии начального отсчёта гирополукомпаса) с осью прямолинейного участка дороги (или линией, ей параллельной), перед началом и после конца закругления дороги. Эта погрешность в несколько раз превосходит погрешность отсчитывания по гирополукомпасу, поэтому погрешность измерения угла поворота почти полностью определяется величиной погрешности ![]() .
.
Соотношения (3.2), (3.3), (3.4), (3.5) позволяют оценить точность определения угла поворота, однако они же являются полным и окончательным решением задачи. Как указывалось, наиболее полные и достоверные оценки метрологических характеристик дорожной лаборатории можно получить из сравнения угловых и линейных величин, полученных с его помощью, с соответствующими величинами, полученными на основе геодезических измерений. Ниже рассматриваются теоретические основы и методика сравнения указанных данных.
Для сравнения углов поворота, полученных с помощью дорожной лаборатории ( ![]() ) и на основе геодезических измерений (
) и на основе геодезических измерений ( ![]() ), на закруглении необходимо определить точки НЗ и КЗ. Если закругление состоит полностью из круговой кривой, то это будут точки НК и КК. Если же в конструкции закругления имеются переходные кривые, то это будут точки НПК (начало переходной кривой). В последнем случае на закруглении необходимо выделить НК и КК круговой кривой, так как все изложенное ниже относится к методике метрологических испытаний лаборатории на круговых кривых.
), на закруглении необходимо определить точки НЗ и КЗ. Если закругление состоит полностью из круговой кривой, то это будут точки НК и КК. Если же в конструкции закругления имеются переходные кривые, то это будут точки НПК (начало переходной кривой). В последнем случае на закруглении необходимо выделить НК и КК круговой кривой, так как все изложенное ниже относится к методике метрологических испытаний лаборатории на круговых кривых.
Точку НЗ определяем с помощью теодолита. Для этого в точке N на кромке покрытия устанавливают теодолит, а в точке M (то же на кромке покрытия) устанавливают веху. Визируют на веху М и трубу переводят через зенит. Речник А начинает двигаться от теодолита N в сторону середины закругления. В момент, когда рейка начинает смещаться с перекрестия сетки трубы, точку фиксируют на кромке покрытия. Аналогичным образом фиксируют точки при движении речника А в сторону от середины закругления к теодолиту. Расстояние между полученными точками делят пополам и построенную таким образом точку принимают за НЗ (НК. Для повышения точности решения задачи наблюдения рекомендуется производить при КП и КЛ.
Точки M,N и А необходимо выбирать на кромке покрытия тщательно, с учётом следующих соображений. Кромка покрытия не является идеальной линией, точно совпадающей с круговой кривой закругления. Её отклонения от указанных кривых обусловлены погрешностями разбивки оси и проезжей части закругления, погрешностями строительных работ и, наконец, разрушением и загрязнением при эксплуатации дороги.
Погрешности разбивки оси дороги на закруглении связаны с тем, что плавная круговая кривая заменяется хордами длиною S=10,15,20 м. Середины хорд отклоняются от круговой кривой на величину «стрелы» ![]() , которая проявляет себя как погрешность разбивочных работ. Из табл. 3.1 видно, что при хордах S=10 и 20 м стрелы f в зависимости от радиуса круговой кривой изменяются в широких пределах.
, которая проявляет себя как погрешность разбивочных работ. Из табл. 3.1 видно, что при хордах S=10 и 20 м стрелы f в зависимости от радиуса круговой кривой изменяются в широких пределах.
Если полагать, что при хордах ![]() м точки оси дороги разбивают также и от их середин построением перпендикуляров длиною
м точки оси дороги разбивают также и от их середин построением перпендикуляров длиною ![]() (
( ![]() – угол, соответствующий хорде S), то погрешности разбивки оси при
– угол, соответствующий хорде S), то погрешности разбивки оси при ![]() м не выйдут за пределы 6,5 см.
м не выйдут за пределы 6,5 см.
Допускаемые проектные отклонения от проектных размеров ширины покрытия равны: для асфальтобетонных покрытий ![]() СМИ для цементобетонных
СМИ для цементобетонных ![]() см.
см.
Таблица 3.1 – Зависимость величин f от радиуса кривой R
|
Радиус круговой кривой R, м |
Стрела f, см |
|
|
При S=10 м |
При S=20 м |
|
|
1000 |
1,2 |
5,0 |
|
800 |
1,6 |
6,3 |
|
600 |
2,1 |
8,3 |
|
400 |
3,1 |
12,5 |
|
200 |
6,3 |
25,0 |
|
100 |
12,5 |
50,0 |
Погрешность положения кромки составит при этом соответственно ![]() 7 и
7 и ![]() 3,5 см.
3,5 см.
Погрешность положения кромки, связанные с её загрязнением и разрушением при эксплуатации оценивается величиной 2-3 до 20-25 см [25]. В среднем она, по-видимому, не превышает 10-11 см.
Таким образом, суммарная величина случайного отклонения кромки покрытия от круговой кривой будет равна
![]() см.
см.
Если погрешность ![]() см считать предельной, то средняя (квадратическая) будет равна
см считать предельной, то средняя (квадратическая) будет равна ![]() см. Естественно, значения 1 весьма существенно зависит от качества строительных работ, типа покрытия, и на дорогах разных категорий может различаться значительно. Ниже изложена методика определения значения 1 для каждого конкретного закругления.
см. Естественно, значения 1 весьма существенно зависит от качества строительных работ, типа покрытия, и на дорогах разных категорий может различаться значительно. Ниже изложена методика определения значения 1 для каждого конкретного закругления.
Для уменьшения искажающего влияния величины 1 на точность и надёжность определения точек НЗ и КЗ на закруглении рекомендуется следующий приём. В местах разметки точек M и N, а также установки рейки А на кромке проезжей покрытия провести мелом огибающие линии по выступам и впадинам извилин кромки и в полученном «коридоре», на осевой его линии, разметить указанные точки (рис. 8.3). Таким путём достигается выравнивание линии кромки покрытия и приближение её к идеальной кривой закругления.
Для определения возможно более точного значения угла поворота оси дороги необходимо произвести его измерение теодолитом. С этой целью на кромке покрытия, примерно на середине закругления устанавливают теодолит и измеряют угол ![]() при КП и КЛ. Среднее значение – это среднее арифметическое, принимают за окончательное значение угла
при КП и КЛ. Среднее значение – это среднее арифметическое, принимают за окончательное значение угла ![]() .
.
Угол поворота оси дороги, полученный измерением с помощью теодолита, равен ![]() . При этом выбор точки, в которой следует устанавливать теодолит при измерении
. При этом выбор точки, в которой следует устанавливать теодолит при измерении ![]() , не оказывает влияния на его величину, так как вершина угла всегда остаётся на кривой, а сам угол будет опираться на одну и ту же хорду АС. С этой точки зрения для измерения угла
, не оказывает влияния на его величину, так как вершина угла всегда остаётся на кривой, а сам угол будет опираться на одну и ту же хорду АС. С этой точки зрения для измерения угла ![]() не требуется точного определения положения середины закругления. Вполне достаточно для установки теодолита эту точку определить на глаз или даже выбрать произвольно.
не требуется точного определения положения середины закругления. Вполне достаточно для установки теодолита эту точку определить на глаз или даже выбрать произвольно.
Вместе с тем погрешности определения положений точек НЗ и КЗ на закруглении, а также отклонения кромки покрытия от идеальной круговой кривой на закруглении и от прямых линий на прямолинейных участках дороги (до точки НЗ и после точки КЗ) весьма существенно влияют на точность измерения угла ![]() . Поэтому при установке вешек в точках НЗ и КЗ, а также теодолита в точке СК необходимо, как указано выше, провести мелом огибающие по выступам и впадинам линии кромки покрытия и на осевых линиях этих «коридоров» окончательно выбрать точки НЗ, СЗ, КЗ.
. Поэтому при установке вешек в точках НЗ и КЗ, а также теодолита в точке СК необходимо, как указано выше, провести мелом огибающие по выступам и впадинам линии кромки покрытия и на осевых линиях этих «коридоров» окончательно выбрать точки НЗ, СЗ, КЗ.
Угол поворота ![]() можно получить также, если в точках НЗ, СЗ и КЗ измерить соответственно углы
можно получить также, если в точках НЗ, СЗ и КЗ измерить соответственно углы ![]() ,
, ![]() . Углы
. Углы ![]() в точках НЗ и КЗ можно измерить следующим образом. В точке НЗ устанавливают теодолит и приводят его в рабочее положение. На расстоянии 40-60 м от точки НЗ на прямолинейном участке дороги (на кромке покрытия) устанавливают вешку. Трубу теодолита при КП наводят на эту вешку и берут отсчёт по горизонтальному кругу. Затем трубу переводят через зенит, наводят на точку СК и берут отсчёт по тому же кругу. Разность отсчётов даёт угол
в точках НЗ и КЗ можно измерить следующим образом. В точке НЗ устанавливают теодолит и приводят его в рабочее положение. На расстоянии 40-60 м от точки НЗ на прямолинейном участке дороги (на кромке покрытия) устанавливают вешку. Трубу теодолита при КП наводят на эту вешку и берут отсчёт по горизонтальному кругу. Затем трубу переводят через зенит, наводят на точку СК и берут отсчёт по тому же кругу. Разность отсчётов даёт угол ![]() . Далее угол
. Далее угол ![]() измеряют повторно при КЛ. Аналогично измеряют угол
измеряют повторно при КЛ. Аналогично измеряют угол ![]() в точке КЗ.
в точке КЗ.
Контроль: должно выполняться условие ![]() , то есть удвоенное значение угла
, то есть удвоенное значение угла ![]() , измеренного в точке СЗ, должно быть равно сумме углов, измеренных в точках НЗ, СЗ, КЗ. Так как углы
, измеренного в точке СЗ, должно быть равно сумме углов, измеренных в точках НЗ, СЗ, КЗ. Так как углы ![]() и
и ![]() измеряются с некоторыми погрешностями, то поставленное условие почти никогда не будет выполняться строго. Несоответствие левой и правой частей условия не должно превышать примерно величины
измеряются с некоторыми погрешностями, то поставленное условие почти никогда не будет выполняться строго. Несоответствие левой и правой частей условия не должно превышать примерно величины ![]() , где
, где ![]() =3438 радиан в минутах; 1 – предельное значение величины отклонения кромки покрытия от круговой кривой (м) с вероятностью 0,7; b – средняя длина сторон, образующих углы
=3438 радиан в минутах; 1 – предельное значение величины отклонения кромки покрытия от круговой кривой (м) с вероятностью 0,7; b – средняя длина сторон, образующих углы ![]() и
и ![]() в точках НЗ, СЗ, КЗ.
в точках НЗ, СЗ, КЗ.
Например, при 1=0,05 м и b=50м эта величина будет равна 7-8.
Погрешность угла поворота, измеренного с помощью дорожной лаборатории, можно охарактеризовать разностью
![]() , где
, где ![]() и
и ![]() – значения угла поворота, полученные лабораторией и геодезическим методом.
– значения угла поворота, полученные лабораторией и геодезическим методом.
Вместе с тем разность ![]() есть результат действия случайных погрешностей при измерениях
есть результат действия случайных погрешностей при измерениях ![]() и
и ![]() , то есть
, то есть
![]() , (3.6)
, (3.6)
Откуда погрешность измерения угла поворота с помощью дорожной лаборатории будет равна
![]() . (3.7)
. (3.7)
Погрешность измерения угла теодолитом очень мало зависит от инструментальной погрешности и почти полностью определяется влиянием погрешностей положения точек НЗ и КЗ, а также отклонениями кромки покрытия на закруглении от идеальной круговой кривой. При этом отклонение кромки от указанной кривой влияют на точность измерения угла ![]() . Так же, как погрешность центрирования теодолита и наблюдаемых точек (сигналов).
. Так же, как погрешность центрирования теодолита и наблюдаемых точек (сигналов).
Влияние погрешностей центрирования теодолита и сигналов на точность измерения угла ![]() выражается формулой
выражается формулой
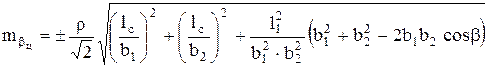 , где
, где ![]() ,
, ![]() – погрешности центрирования сигналов и теодолита;
– погрешности центрирования сигналов и теодолита; ![]() ,
, ![]() – длины сторон, образующих угол
– длины сторон, образующих угол ![]() .
.
Если ![]() ,
, ![]() и
и ![]() , то
, то ![]() .
.
Так как ![]() , то погрешность измерения угла
, то погрешность измерения угла ![]() , обусловленная отклонением кромки покрытия от круговой кривой, будет равна
, обусловленная отклонением кромки покрытия от круговой кривой, будет равна ![]() . (3.8)
. (3.8)
В формулу (3.8) входит величина 1, предельное значение которой с заданной вероятностью можно определит на основе следующих исследований. На кромке покрытия на закруглении разбивают через каждые 1-2 точки и мелом проводят в этих местах огибающие по выступам и впадинами извилистой линии кромки . С помощью сантиметровой линейки измеряют ширину построенного «коридора» около каждой точки и делят её пополам. Полученные значения 1 заносят в соответствующие классы таблицы распределения (табл. 3.2). Далее подсчитывают численности и частости классов. Чтобы определить предельное значение 1 с заданной вероятностью, в графе «частость класса» подсчитывают нарастающим итогом частости классов, начиная с самого верхнего. Известно, что при нормальном законе распределения погрешностей средняя квадратическая погрешность m имеет вероятность 0,684. В связи с этим предельное отклонение 1, имеющее вероятность ~0,68, будет соответствовать среднеквадратическую значению.
Чтобы определить предельное значение величины 1 с вероятностью ~0,68, необходимо в графе «частость класса» подсчитать нарастающим итогом сумму частостей, равную~68 %. Среднее значение 1 в классе, частость которого дополняет сумму частостей предыдущих классов до 68 % и будет равно предельному значению её с вероятностью 0,68.
8,5+17,8+30,3=56,3%. Так как частость 16,3 % в классе (3-4) дополняют сумму 56,3 % до 72,9 % (которая наиболее близка к 68 %), то предельное значение 1 с вероятностью ~0,7 будет равно примерно 3-3,5 см.
Таблица 3.2 – Таблица распределения значения
|
Классы значений 1, см от-до |
Численность класса n |
Частость класса, % |
|
0-1 |
11 |
8,5 |
|
1-2 |
23 |
17,8 |
|
2-3 |
39 |
30,3 |
|
3-4 |
21 |
16,3 |
|
4-5 |
14 |
10,8 |
|
5-6 |
9 |
7,0 |
|
6-7 |
7 |
5,4 |
|
7-8 |
5 |
3,9 |
|
Сумма |
129 |
100 |
Число значений 1, измеренных на кромке покрытия закругления, должно быть достаточно большим (![]() ).
).
Рассмотрим влияние погрешностей определения положения точек НЗ и КЗ на кривой закругления на точность измерения угла ![]() . Как показано в работе [24], влияние указанных погрешностей на точность измерения угла
. Как показано в работе [24], влияние указанных погрешностей на точность измерения угла ![]() определяется формулой
определяется формулой
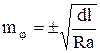 , где
, где ![]() – погрешность измерения угла
– погрешность измерения угла ![]() , обусловленная погрешностями положения точек НЗ и КЗ на закруглении;
, обусловленная погрешностями положения точек НЗ и КЗ на закруглении; ![]() – радиан в минутах; 1 – предельное отклонение кромки покрытия от круговой кривой с вероятностью 0,68;
– радиан в минутах; 1 – предельное отклонение кромки покрытия от круговой кривой с вероятностью 0,68; ![]() – расстояния; R – радиус круговой кривой.
– расстояния; R – радиус круговой кривой.
Так как ![]() , то
, то 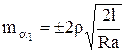 . (3.9)
. (3.9)
Суммарное влияние погрешностей ![]() и
и ![]() на точность измерения угла
на точность измерения угла ![]() будет равно
будет равно
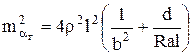 (3.10)
(3.10)
Подставляя значение ![]() в (8.7), получим
в (8.7), получим
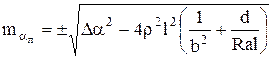 (3.11) где
(3.11) где ![]() – разность значений угла поворота оси дороги, измеренных дорожной лабораторией и теодолитом; остальные обозначения прежние.
– разность значений угла поворота оси дороги, измеренных дорожной лабораторией и теодолитом; остальные обозначения прежние.
Формула (3.11) является окончательной рабочей. Она позволяет оценивать точность измерения углов поворота ![]() оси дороги на закруглениях с помощью дорожной лаборатории. При этом разность
оси дороги на закруглениях с помощью дорожной лаборатории. При этом разность ![]() можно вычислять по значениям
можно вычислять по значениям ![]() , полученным из одного, двух, трёх, четырёх и т.п. проездов лаборатории. Таким путём можно проследить, как изменяется погрешность
, полученным из одного, двух, трёх, четырёх и т.п. проездов лаборатории. Таким путём можно проследить, как изменяется погрешность ![]() в зависимости от осреднения результатов (количества челночных проездов) и определять оптимальное число проездов.
в зависимости от осреднения результатов (количества челночных проездов) и определять оптимальное число проездов.
Анализ данных, полученных по формуле (3.11), необходимо проводить совместно с анализом данных, полученных по формулам (3.2), (3.3), (3.4) и (3.5).
Точность измерения длины круговой кривой с помощью дорожной лаборатории может быть определена следующим образом.
После установления положения точек НЗ и КЗ измеряют с помощью оптического дальномера длину кривой закругления между этими точками. Длину кривой можно вычислить также по формуле
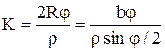 . (3.12) где
. (3.12) где ![]() .
.
Равенство длины кривой, полученной измерением дальномером, и вычисленной по формуле (3.12), может служить контролем и оценкой точности результатов геодезических измерений.
Если продифференцировать выражение (3.12) и перейти к средним квадратическим погрешностям, то погрешность определения длины кривой по (3.12) будет 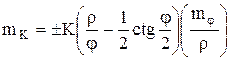 , где
, где ![]() , с вероятностью 0,95 разность между непосредственно измеренным и вычисленным значениями длины кривой не должна превышать
, с вероятностью 0,95 разность между непосредственно измеренным и вычисленным значениями длины кривой не должна превышать ![]() .
.
Далее измеряют длину кривой закругления с помощью дорожной лаборатории. Погрешность измерения длины кривой с помощью дорожной лаборатории можно охарактеризовать разностью ![]() где
где ![]() и
и ![]() – длина кривой, измеренная с помощью лаборатории и геодезическим методом.
– длина кривой, измеренная с помощью лаборатории и геодезическим методом.
Одновременно разность ![]() равна
равна ![]() . (3.13)
. (3.13)
В работе [24] показано, что погрешность измерения длины кривой, обусловленная неточным определением положения точек НЗ и КЗ, равна 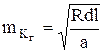 , (3.14) где R – радиус круговой кривой; d, a – расстояния; 1 – предельное отклонение кромки покрытия от круговой кривой с вероятностью ~0,68.
, (3.14) где R – радиус круговой кривой; d, a – расстояния; 1 – предельное отклонение кромки покрытия от круговой кривой с вероятностью ~0,68.
Из формулы (3.14) видно, что для уменьшения погрешности измерения длины кривой точку N (рис. 3.3) при определении начала и конца закругления следует выбирать как можно ближе к началу закругления, а расстояние ![]() достаточно большим, чтобы отношение
достаточно большим, чтобы отношение ![]() мало отличалось от единицы. Эта рекомендация была уже сформулирована раньше без специального доказательства. Указанное, естественно, относится и к выбору точек M, N в конце закругления.
мало отличалось от единицы. Эта рекомендация была уже сформулирована раньше без специального доказательства. Указанное, естественно, относится и к выбору точек M, N в конце закругления.
Подставляя из (3.14) в (3.13) значения ![]() , получим
, получим
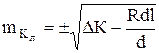 . (3.15)
. (3.15)
Формула (3.15) является рабочей и позволяет оценивать точность определения длины кривой закругления с помощью дорожной лаборатории. Как видно из предыдущего, погрешность при измерении длины кривой с помощью дорожной лаборатории в основном определяется погрешностями положения точек НЗ и КЗ на закруглении. При проездах лаборатории «туда-обратно» по закруглению можно получить среднее значение длины кривой, которое будет в ![]() раз точнее единичного определения этой длины на каждого проезда.
раз точнее единичного определения этой длины на каждого проезда.
Погрешность среднего значения кривой можно вычислить по формуле
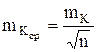 , (3.16) где
, (3.16) где 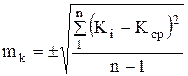 , (3.17)
, (3.17) 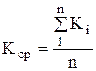 .
.
С помощью формул (3.16), (3.17) можно построить доверительные интервалы для истинного значения длины кривой ![]() по результатам одного и n проездов лаборатории по закруглению. С вероятностью 0,95 такие доверительные интервалы будут
по результатам одного и n проездов лаборатории по закруглению. С вероятностью 0,95 такие доверительные интервалы будут ![]() ,
, ![]() .
.
Отметим, что с вероятностью 0,95 должно выполняться неравенство ![]() , где
, где ![]() и
и ![]() вычисляются соответственно по (3.15) и (3.17). Это может служить контролем правильности наблюдения и вычисления.
вычисляются соответственно по (3.15) и (3.17). Это может служить контролем правильности наблюдения и вычисления.
Исследование устойчивости значений и точности определения длины кривой при различном числе проездов дорожной лаборатории по закруглению «туда-обратно» можно выполнять (как и при исследовании точности измерения угла поворота) путём повторения всех вычислений по ½, 1/3 и ¼ всех значений К. Для этого из n значений К необходимо образовать 2 выборки численностью n/2, 3 выборки численностью n/3 и 4 выборки численностью n/4 и повторить по этим выборкам все вычисления.
Точность измерения радиуса круговой кривой с помощью дорожной лаборатории может быть охарактеризована разностью
![]() , (3.18) где
, (3.18) где ![]() ,
, ![]() – значение радиуса, полученные по данным лаборатории и на основе геодезических измерений.
– значение радиуса, полученные по данным лаборатории и на основе геодезических измерений.
Тогда 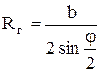 , (3.19) где АВ=ВС= b – измеряются оптическим дальномером.
, (3.19) где АВ=ВС= b – измеряются оптическим дальномером.
Дифференцируя выражение (3.19) по b и ![]() и переходя к средним квадратическим погрешностям, получим
и переходя к средним квадратическим погрешностям, получим 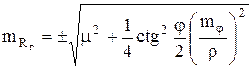 .
.
Относительной погрешностью измерения хорд дальномером 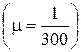 можно пренебречь в связи с её малостью. Так как
можно пренебречь в связи с её малостью. Так как 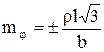 и принимая
и принимая ![]() м; после некоторых преобразования получим
м; после некоторых преобразования получим ![]() .(3.20)
.(3.20)
Одновременно ![]() , (3.21) где
, (3.21) где ![]() ,
, ![]() – средние квадратические погрешности определения радиуса с помощью дорожной лаборатории и геодезическим методом.
– средние квадратические погрешности определения радиуса с помощью дорожной лаборатории и геодезическим методом.
Подставляя в (3.21) значение ![]() на (8.20), будем иметь
на (8.20), будем иметь 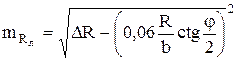 . (3.22)
. (3.22)
Формула (3.22) является окончательной, рабочей. Она позволяет оценивать точность измерения радиуса круговой кривой с помощью дорожной лаборатории.
Важно ещё раз подчеркнуть, что изложенные выше теоретические основы и методика метрологических испытаний лаборатории применимы только на круговой кривой. Теория и методика обследования закругления с целью установления их конструкции и проведения метрологических испытаний лаборатории на закруглениях сложной конструкции требуют особого рассмотрения. Необходимо также исследовать вопрос о зависимости точности оценок геометрических параметров дороги в плане от скорости движения лаборатории. Наконец, самостоятельного рассмотрения и исследования требуют вопросы необходимой точности, которую должна обеспечивать лаборатории при определении различных геометрических параметров дороги в плане, продольном и поперечном профиле.
























