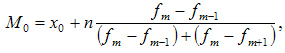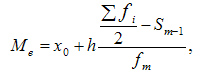Как найти среднее значение в диагностике

Как найти среднее значение в диагностике

  • Помогаю в написании дипломных, курсовых, магистерских работы по психологии, а также рефератов и эссе; контрольных, отчетов по практике и статистических расчетов.

    Я профессиональный психолог и автор работ по психологии с многолетним стажем. Выступаю как индивидуальный предприниматель (ИП): заключаю договор, выдаю чеки об оплате.

    Помогаю студентам-психологам более 15 лет (этот сайт существует с 2007). Качественно и быстро. Помогу даже с очень трудными темами.

    Опишите ситуацию, и я скажу стоимость написания вашей работы.

    УЗНАТЬ СТОИМОСТЬ

Описательные статистики

Первичные описательные статистики – это наиболее простые характеристики, которыми можно описать психологические данные, которые были получены в ходже тестирования испытуемых.

К наиболее часто используемым в курсовых и дипломных по психологии описательным статистикам можно отнести:

  • среднее значение;
  • стандартное отклонение.

Среднее значение

Простейшая математическая процедура, которую необходимо освоить студенту-психологу при написании диплома – расчет среднего значения.

Среднее значение или среднее арифметическое – это число, получаемое как сумма нескольких показателей, деланная на количество этих показателей. Например, в результате тестирования были получены показатели тревожности в группе из 10-ти человек. Чтобы получить среднее значение тревожности по группе нужно сложить показатели всех испытуемых, а затем получившуюся сумму разделить на 10.

Среднее значение характеризует группу целиком. Зная среднее можно оценить показатели каждого испытуемого относительно остальных. Например, измеряемая в приведённом выше примере тревожность могла быть от 1 до 5 баллов. Пусть средняя по группе тревожность оказалась 3,5 балла. Тогда, показатель испытуемого в 4 балла можно считать относительно высоким, а в 2 балла- относительно низким.

Среднее значение относится к показателям центральной тенденции и отражает степень выраженности показателя в группе. Стандартное отклонение отражает степень изменчивости признака в группе, но о нем речь впереди.

Среднее значение какого-либо показателя характеризует группу в целом и позволяет сравнивать ее с другими группами. Например, проведена диагностика уровня эмпатии в группе мужчин и женщин. Как узнать, влияет ли пол на способность к эмпатии. Один из способов – найти средний уровень этого показателя в группах мужчин и женщин. Например, в группе женщин средний уровень эмпатии равен 23,5 баллов, а в группе мужчин – 17,7 баллов. Как видно, в среднем у женщин эмпатия выше, чем у мужчин.

Важно отметить, среднее значение – это не просто число, а – статистическое – полученное в результате особой процедуры. Поэтому и сравнивать средние значения как обычные числа нельзя. Для сравнения средних значений используются дополнительные процедуры – расчет статистических критериев. Например, U-критерий Манна-Уитни или t-критерий Стъюдента.

Среднее – это не единственный статистический показатель, который отражает выраженность переменной в группе. Аналогичную функцию выполняют мода и медиана. Однако они редко используются в дипломах по психологии.

Средние значения выраженности психологических показателей в курсовой или дипломной по психологии представляются в виде таблиц и диаграмм. В таблицах среднее обозначается буквой «М».

Стандартное отклонение

Если среднее арифметическое отражает выраженность показателя в группе, то стандартное отклонение (среднеквадратичное отклонение) показывает его разброс данных или изменчивость. Чем больше величина стандартного отклонения, тем больше разброс показателей в группе испытуемых.

Например, группу мальчиков протестировали методикой на выявление уровня эгоцентризма, показатели которого изменяются от 1 до 10. Расчет среднего показал М=6,5, а стандартное отклонение σ=3 (стандартное отклонение обозначается буквой «сигма»). Эти данные позволяют нам говорить о том, что подавляющее большинство показателей эгоцентризма мальчиков укладываются в диапазон от 3,5 до 9,5 (среднее плюс/минус стандартное отклонение – М ± σ).

Если при тестировании группы девочек среднее значение М=5, а стандартное отклонение σ=1, то большинство испытуемых этой группы имеют эгоцентризм в диапазоне от 4 до 6 (5 ± 1).

Анализирую такие данные в дипломе по психологии можно указать, что средний уровень эгоцентризма у мальчиков больше, чем у девочек. При этом разброс показателей эгоцентризма у мальчиков также больше, чем у девочек, то есть, в группе мальчиков есть испытуемые с очень низкими и очень высокими показателями относительно среднего. У девочек показатели менее «разбросаны» относительно среднего.

Расчет среднего и стандартного отклонения

Формула расчета среднего очень проста и этот параметр можно рассчитать вручную.

Пример расчёта среднего

В таблице приведены показатели, полученные по тесту диагностики уровня одиночества у 64-х испытуемых.

№ исп.

Уровень одиночества

1

13

2

14

3

5

4

11

5

17

6

9

7

18

8

6

9

9

10

9

11

15

12

14

13

7

14

9

15

8

16

13

17

12

18

14

19

19

20

15

21

11

22

15

23

6

24

8

25

8

26

8

27

5

28

20

29

5

30

9

31

7

32

7

33

11

34

15

35

7

36

7

37

9

38

8

39

11

40

17

41

10

42

18

43

15

44

14

45

15

46

4

47

8

48

15

49

17

50

14

51

4

52

8

53

18

54

14

55

14

56

9

57

1

58

7

59

11

60

4

61

14

62

11

63

6

64

17

Найдем средний уровень переживания одиночества в группе.

М=(13 + 14+ 5+ 11+ 17+ 9+ 18+ 6+ 9+ 15+ 14+ 7+ 9+ 8+ 13+ 12+ 14+ 19+ 15+ 11+ 15+ 6+ 8+ 8+ 8+ 5+ 20+ 5+ 9+ 7+ 7+ 11+ 15+ 7+ 7+ 9+ 8+ 11+ 17+ 10+ 18+ 15+ 14+ 15+ 4+8+15+17+14+4+8+18+14+14+9+1+7+11+4+14+11+6+17)  / 64=10,92

Как видим, если испытуемых достаточно много, то рассчитывать среднее вручную задача трудоемкая.

Еще более трудоемкий процесс – расчёт стандартного отклонения. Не буду утомлять вас формулами, скажу лишь, что расчёт этого показателя сводится к тому, что суммируются квадраты разности показателей со средним значением. Затем эта сумма делится на число показателей и из полученного числа извлекается квадратный корень. Вручную такие вычисления делать хлопотно, и не нужно.

Чаще всего расчеты среднего и стандартного отклонения можно делать в статистических программах STATISTICA, SPSS и электронных таблицах Exсel.

Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать

Источник

МАОУ лицей №27

Диагностика
педагогического процесса в средней группе (с 4 до 5 лет)

Диагностика образовательного процесса в
средней группе.

Предлагаемая диагностика разработана с целью
оптимизации образователь­ного процесса в любом учреждении, работающим с группой
детей 4—5 лет, вне зависимости от приоритетов разработанной программы обучения
и вос­питания и контингента детей. Это достигается путем использования обще­принятых
критериев развития детей данного возраста и уровневым подхо­дом к оценке
достижений ребенка по принципу: чем ниже балл, тем боль­ше проблем в развитии
ребенка или организации педагогического процесса в группе детей. Система
мониторинга содержит 5 образовательных облас­тей, соответствующих Федеральному
государственному образовательно­му стандарту дошкольною образования, приказ
Министерства образования и науки № 1155 от 17 октября 2013 года:
«Социально-коммуникативное раз­витие», «Познавательное развитие», «Речевое
развитие», «Художествснно- эстетичсскос развитие», «Физическое развитие», что
позволяет комплексно оценить качество образовательной деятельности в группе и
при необходимо­сти индивидуализировать его для достижения достаточного уровня
освоения каждым ребенком содержания образовательной программы учреждения.

Оценка педагогического процесса связана с
уровнем овладения каждым ребенком необходимыми навыками и умениями по
образовательным облас­тям:

1   балл – ребенок не может выполнить все
параметры оценки, помощь взрослого не принимает;

2   балла ребенок с помощью взрослого выполняет
некоторые парамет­ры оценки;

3   балла — ребенок выполняет все параметры оценки
с частичной помо­щью взрослого;

4   балла — ребенок выполняет самостоятельно и с
частичной помощью взрослого все параметры оценки;

5   баллов — ребенок выполняет все параметры
оценки самостоятельно.

Таблицы педагогической диагностики заполняются
дважды в год, если

другое не предусмотрено в образовательной организации,
— в начале и кон­це учебного года (лучше использовать ручки разных цветов), для
проведения сравнительного анализа. Технология работы с таблицами проста и
включает 2 этапа.

Этап 1. Напротив фамилии и имени каждого ребенка
проставляются бал­лы в каждой ячейке указанного параметра, по которым затем
считается ито­говый показатель по каждому ребенку (среднее значение = все баллы
сложить (но строке) и разделить на количество параметров, округлять до десятых
до­лей). Этот показатель необходим для написания характеристики на конкрет­ного
ребенка и проведения индивидуального учета промежуточных результа­тов освоения
общеобразовательной программы.

Этап 2. Когда все дети прошли диагностику, тогда
подсчитывается итого­вый показатель по группе (среднее значение = все баллы
сложить (по столб­цу) и разделить на количество параметров, округлять до десятых
долей). Этот показатель необходим для описания обще групповых тенденций (в
группах компенсирующей направленности — для подготовки к групповому медико-
психолого-педагогическому совещанию), а также для ведения учета обще групповых
промежуточных результатов освоения общеобразовательной про­граммы.

Двухступенчатая система мониторинга позволяет
оперативно находить неточности в построении педагогического процесса в группе и
выделять де­тей с проблемами в развитии. Это позволяет своевременно
разрабатывать для детей индивидуальные образовательные маршруты и оперативно
осу­ществлять психолого-методическую поддержку педагогов. Нормативными
вариантами развития можно считать средние значения по каждому ребен­ку или обще
групповому параметру развития больше 3,8. Эти же параметры в интервале средних
значений от 2,3 до 3,7 можно считать показателями про­блем в развитии ребенка
социального и/или органического генеза, а также незначительные трудности
организации педагогического процесса в группе. Средние значения менее 2,2 будут
свидетельствовать о выраженном несоот­ветствии развития ребенка возрасту, а
также необходимости корректировки педагогического процесса в группе по данному
параметру данной образо­вательной области. (Указанные
интервалы средних значений носят реко­мендательный характер, так как получены с
помощью применяемых в психолого-педагогических исследованиях психометрических
процедур, и будут уточняться по мере поступления результатов мониторинга детей
данного возраста.)

Наличие математической обработки
результатов педагогической диагно­стики образовательного процесса оптимизирует
хранение и сравнение ре­зультатов каждого ребенка и позволяет своевременно
оптимизировать педа­гогический процесс в группе детей образовательной
организации

Рекомендации по описанию
инструментария педагогической диагностики в средней группе

Инструментарий педагогической диагностики
представляет собой описа­ние тех проблемных ситуаций, вопросов, поручений,
ситуаций наблюдения, которые вы используете для определения уровня сформированное™
у ребенка того или иною параметра оценки. Следует отметить, что часто в период
про­ведения педагогической диагностики данные ситуации, вопросы и поручения
могут повторяться, с тем чтобы уточнить качество оцениваемого параметра. Это
возможно, когда ребенок длительно отсутствовал в группе или когда име­ются
расхождения в оценке определенного параметра между педагогами, ра­ботающими с
этой группой детей. Музыкальные и физкультурные руководите­ли, педагоги
дополнительного образования принимают участие в обсуждении достижений детей
группы, но разрабатывают свои диагностические критерии в соответствии со своей
должностной инструкцией и направленностью образо­вательной деятельности.

Важно отметить, что каждый параметр
педагогической оценки может быть диагностирован несколькими методами, с тем
чтобы достичь определенной точности. Также одна проблемная ситуация может быть
направлена на оценку нескольких параметров, в том числе из разных
образовательных областей.

Основные диагностические методы педагога
образовательной организа­ции:

·       
наблюдение;

·       
проблемная
(диагностическая) ситуация;

·       
беседа.

Формы проведения педагогической диагностики:

·       
индивидуальная;

·       
подгрупповая;

·       
групповая.

Обратите внимание, что диагностируемые
параметры могут быть расши­рены / сокращены в соответствии с потребностями
конкретного учреждения, поэтому описание инструментария педагогической
диагностики в разных образовательных организациях будет различным. Это объясняется
разным наполнением развивающей среды учреждений, разным контингентом воспи­танников,
разными приоритетными направлениями образовательной деятель­ности конкретной
организации.

Примеры описания инструментария по
образовательным областям

Образовательная область
«Социально-коммуникативное развитие»

1.   Старается соблюдать правила поведения в
общественных местах, в об­щении со взрослыми и сверстниками, в природе.

Методы: наблюдение в быту и в организованной
деятельности, проблем­ная ситуация.

Форма проведения: индивидуальная,
подгрупповая, групповая.

Задание: фиксировать на прогулке, в
самостоятельной деятельности стиль поведения и общения ребенка.

Материал: игрушки мышка и белка, макет норки
на полянке и дерева с дуплом.

Задание: «Пригласи Муравья к Белочке в гости».

2.   Понимает социальную оценку поступков
сверстников или героев ил­люстраций, литературных произведений, эмоционально
откликается.

Методы: беседа, проблемная ситуация.

Материал: сказка «Два жадных медвежонка».

Форма проведения: индивидуальная,
подгрупповая.

Задание: «Почему медвежата расстроились?
Почему лиса радовалась? Кто поступил правильно? Кто поступил нечестно? Почему?»

3.   Имеет представления о мужских и женских
профессиях.

Методы: проблемная ситуация.

Материал: картинки с изображением профессий
без указания на пол, ат­рибуты профессий, кукла-девочка, кукла-мальчик.

Форма проведения: индивидуальная,
подгрупповая.

Задание: «Разложите картинки так, кто кем мог
бы работать. Почему?»

Образовательная область
«Познавательное развитие»

1.   Знает свои имя и фамилию, адрес проживания,
имена родителей.

Методы: беседа.

Форма проведения: индивидуальная.

Задание: «Скажи, пожалуйста, как тебя зовут?
Как твоя фамилия? Где ты живешь? На какой улице? Как зовут папу/маму?»

2.   Умеет группировать предметы по цвету, размеру,
форме, назначению.

Методы: проблемная ситуация.

Материал: круг, квадрат, треугольник,
прямоугольник, овал одного цвета и разного размера, муляжи и картинки овощей,
фруктов, кукольная посуда/ одежда/мебель.

Форма проведения: индивидуальная,
подгрупповая.

Задание: «Найди, что к чему подходит по цвету,
размеру, форме, назна­чению».

Образовательная
область «Речевое развитие»

1. Поддерживает беседу, использует всс части
речи. Понимает и употреб­ляет слова-антонимы.

Методы: проблемная ситуация, наблюдение.

Материал: опытно-экспериментальная
деятельность «Пузырьки воздуха в воде», ситуация ответа детей на вопрос
взрослого.

Форма проведения: индивидуальная,
подгрупповая.

Задание: «Как увидеть воздух? Можно подуть в
трубочку в стакан с во­дой. Это пузырьки воздуха. Что легче — воздух или вода?
Почему?»

Образовательная
область «Художественно-эстетическое развитие»

1. Узнает песни по мелодии. Может петь
протяжно, четко произносить слова; вместе с другими детьми — начинать и
заканчивать пение.

Методы: проблемная ситуация, наблюдение.

Материал: ситуация пения детьми знакомой песни
(на выбор).

Форма проведения: подгрупповая, групповая.

Задание: «Сейчас все вместе будем петь песню».

Образовательная
область «Физическое развитие»

1.  Ловит мяч с расстояния. Метает мяч разными
способами правой и ле­вой руками, отбивает о иол.

Методы: проблемная ситуация, наблюдение в быту
и организованной де­ятельности.

Материал: мяч, корзина, стойка-цель.

Форма проведения: индивидуальная,
подгрупповая.

Задание: «Попади в корзину мячом
правой рукой, потом левой рукой. Теперь попробуем попасть в стойку-цель. Теперь
играем в игру «Лови мяч и отбивай»».

Образовательная область
«Познавательное развитие»

Воспитатели ________________________________________________________                                         
Группа ________________________________________

№ п/п

Ф.И.О.

ребенка

Знает свои имя и фамилию, ад­рес проживании, имена родителей

Рассматривает иллюстрирован­ные издания де­тских
книг, про­являет интерес к ним

Знает о значении солнца, воздуха, воды для чело­века

Ориентируется
в пространстве (на себе, на другом человеке, от предмета, на плоскости)

Называет
диких и домашних животных, одежду, обувь, мебель, посуду, деревья

Сравнивает
количество предметов в группах на основе счета до 5, приложением, наложением

Различает
круг, квадрат, треугольник, прямоугольник

Умеет
группировать предметы по цвету, размеру, форме, назначению

Понимает смысл слов «утро», «вечер»,
«день», «ночь», определяет части суток, называет времена года, их признаки,
последовательность

Итоговый
показатель по каждому ребенку (среднее значение)

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

Итоговый показа­тель
по группе (сред­нее значение)

Образовательная область «Речевое развитие»

№ п/п

Ф.И.О.

ребенка

Рассказывает о содержании сю­жетной картинки, в том
числе по опорной схеме. Может повторить образцы описания игрушки

Имеет предпочтение в
литературных произведени­ях Проявляет эмоциональную заинтересованность в
драматизации знакомых сказок. Может переска­зать сюжет литературного
произведения, заучить стихотворение наизусть

Определяет первый звук в сло­ве. Умеет образовывать
новые слова по аналогии со знакомы­ми словами

Поддерживает беседу, ис­пользует все част речи.
Понимает и употребляет слова-антонимы

Итоговый показатель по каждому ребенку (среднее
значение)

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

Итоговый показа­тель
по группе (сред­нее значение)

Воспитатели
________________________________________________________                                         
Группа________________________________________

Образовательная область «Физическое  развитие»

№ п/п

Ф.И.О.

ребенка

Знает о значении для
здоровья утренней гим­настики, закаливания, соблюдения режима дня

Соблюдает элементарные правила личной ги­гиены,
опрятности

Умеет самостоятель­но одеваться и разде­ваться,
убирает одежду и обувь в шкафчик

Ловит мяч с расстоя­ния.
Метает мяч разны­ми способами правой и левой руками, отбива­ет о пол

Строится по заданию взрослого в шеренгу, в колонну по
одному, парами, в круг

Итоговый показатель
по каждому ребенку (среднее значение)

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

Итоговый показа­тель
по группе (сред­нее значение)

Воспитатели
________________________________________________________                                         
Группа _______________________________________

Образовательная область «Социально-коммуникативное развитие»

№ п/п

Ф.И.О.

ребенка

Старается соблюдать
правила поведения в общественных местах, н общении со взрослыми и сверст­никами,
к природе

Понимает социальную оценку поступков сверстников или
героев иллюстраций, ли­тературных произве­дений, -эмоционально откликается

Понимает значение слов обозначающих эмоциональное
состояние, этические ка­чества, эстетические характеристики

Имеет представления о мужских и женских профессиях.

Проявляет интерес к кукольному театру, выбирает
предпочитаемых героев, может поддерживать ролевые диалоги

Готовит к занятиям рабочее место, убирает материалы
по окончании работы

Принимает роль в
игре со сверстниками, проявляет инициативу в игре, может объяснить сверстнику
правило игры

Итоговый показатель
по каждому ребенку (среднее значение)

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

Итоговый показа­тель
по группе (сред­нее значение)

Воспитатели
________________________________________________________                                         
Группа ________________________________________

Образовательная область «Художественно-эстетическое  развитие»

№ п/п

Ф.И.О.

ребенка

Способен
преобразовывать постройки в соответствии с заданием взрослого, проявляет
интерес к конструктивной деятельности, в том числе к поделкам из бумаги

Правильно
держит ножницы и умеет резать ими по прямой, по диагонали (квадрат и
прямоугольник); вырезать круг из квадрата, овал – из прямоугольника, плавно
срезать и закруглять углы

Изображает
предметы путем отчетливых форм, подбора цвета, аккуратного закрашивания,
приклеивания, использования разных материалов. Объединяет предметы в сюжеты

Знаком с
элементами некоторых видов народного прикладного творчества, может
использовать их в своей творческой деятельности

Имеет
предпочтение в выборе муз. произведения для слушания и пения. Выполняет
движения, отвечающие характеру музыки, самостоятельно меняя их в соответствии
с двухчастной формой музыкального произведения

Умеет
выполнять танцевальные движения: пружинка, подскоки, движение парами по
кругу, кружение по одному и в парах. Может выполнять движения с предметами

Узнает песни по
мелодии.

Может петь протяжно,
четко произносить слова; вместе с другими детьми – начинать и заканчивать
пение

Итоговый показатель
по каждому ребенку (среднее значение)

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

сентябрь

май

Итоговый показа­тель
по группе (сред­нее значение)

Воспитатели
________________________________________________________                                         
Группа ________________________________________

Выводы:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Выводы:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Источник

Представление результатов исследования

В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.

Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.

Ошибка среднего арифметического

Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.

Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.

Ошибка среднего арифметического обозначается как m или  Представление результатов исследования

Ошибка среднего арифметического рассчитывается по формуле:

Представление результатов исследования

где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.

Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.

Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.

Правила записи результатов исследования

  1. В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
  2. В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
  3. В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.

Представление результатов научных исследований

В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52

В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде:  (М±m) (табл.1).

Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)

Эффективный модуль

упругости (Е), кПа

 Эффективный модуль

вязкости (V), Па с
Этап

эксперимента

 Рассл. Напряж. Рассл. Напряж.
До ФН 7,0±0,3 17,1±1,4 29,7±1,7 46±4
После ФН 7,7±0,3 18,7±1,4 30,9±2,0 53±6

Литература

  1. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
  2. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
  3. Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
  4. Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
  5. Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
Источник

Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.

В чем проблема?

Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.

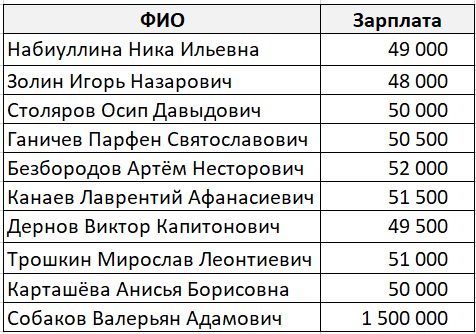
Давайте обратимся к классическому примеру со средней зарплатой.

В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).

Выборка зарплат

Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.

Какие способы вычисления среднего бывают?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

Формула:

  • x – среднее арифметическое;
  • xn – конкретное значение;
  • n – количество значений.

Плюсы:

  • Хорошо работает при нормальном распределении значений в выборке;
  • Легко вычислить;
  • Интуитивно понятно.

Минусы:

  • Не дает реального представления о распределении значений;
  • Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).

Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.

Формула:

  • M0 – мода;
  • x0 – нижняя граница интервала, который содержит моду;
  • n – величина интервала;
  • fm– частота (сколько раз в ряду встречается то или иное значение);
  • fm-1 – частота интервала предшествующего модальному;
  • fm+1 – частота интервала следующего за модальным.

Плюсы:

  • Прекрасно подходит для получения представления об общественном мнении;
  • Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
  • Проста для понимания.

Минусы:

  • Моды может просто не быть (нет повторов);
  • Мод может быть несколько (многомодальное распределение).

Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.

Формула:

Медиана формула

  • Me – медиана;
  • x0 – нижняя граница интервала, который содержит медиану;
  • h – величина интервала;
  • f i – частота (сколько раз в ряду встречается то или иное значение);
  • Sm-1 – сумма частот интервалов предшествующих медианному;
  • fm – число значений в медианном интервале (его частота).

Плюсы:

  • Дает самую реалистичную и репрезентативную оценку;
  • Устойчива к выбросам.

Минусы:

  • Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.

Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).

А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:

  • СРЗНАЧ(число1;[число2];…) — функция для определения среднего арифметического;
  • МОДА.ОДН(число1;[число2];...) — функция моды (в более старых версиях Excel использовалась МОДА(число1;[число2];...));
  • МЕДИАНА(число1;[число2];...) — функция для поиска медианы.

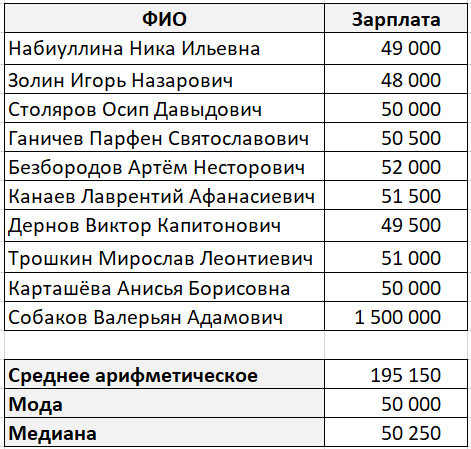
И вот какие значения у нас получились:

Расчет среднего арифметического, моды и медианы

В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.

Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.

Вычисляем среднее арифметическое на SQL

Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция AVG.

И чтобы ее использовать достаточно написать вот такой запрос:

/* Здесь и далее salary - столбец с зарплатами, а employees - таблица сотрудников в нашей базе данных */

SELECT AVG(salary) AS 'Средняя зарплата'
FROM employees

Вычисляем моду на SQL

В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.

Напишем запрос:

/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */
SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты'
FROM employees
GROUP BY salary
ORDER BY COUNT(*) DESC

Вычисляем медиану на SQL

Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей PERCENTILE_CONT.

Выглядит все это так:

/* В данном случае процентиль 0.5 и будет являться медианой */

SELECT TOP(1) PERCENTILE_CONT(0.5)
       WITHIN GROUP (ORDER BY salary)
       OVER() AS 'Медианная зарплата'
FROM employees

Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.

Какой способ все-таки использовать?

Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.

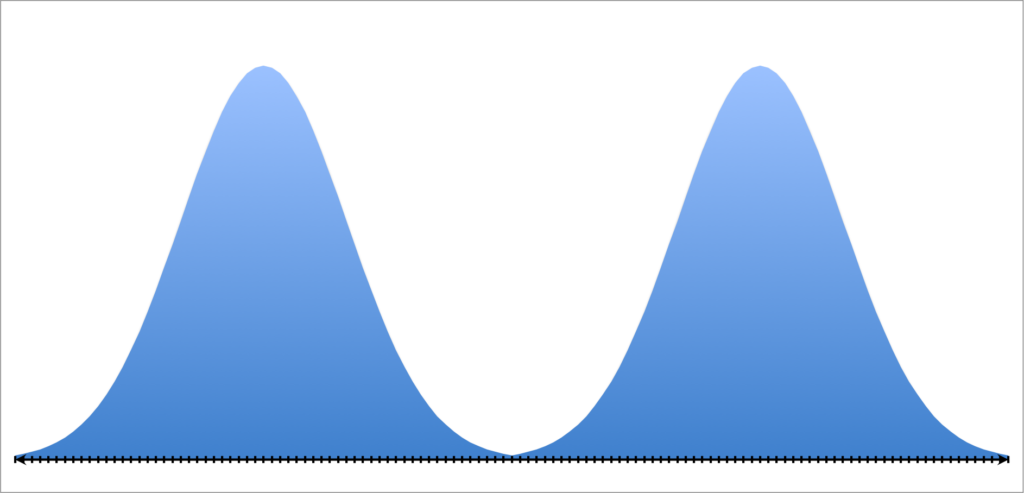
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:

Бимодальное распределение

На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.

В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.

А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.

Вывод:

При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.

Окончательный выбор меры центральной тенденции всегда лежит на аналитике.

Полезные ссылки:

  • SQL и теория вероятностей (YouTube)
  • Анализ нормальности распределения данных (YouTube)
  • Меры центральной тенденции
  • Об авторе
  • Свежие записи

Источник

Добавить комментарий