Иллюстрированный самоучитель по MathCAD 12
В Mathcad имеется ряд встроенных функций для расчетов числовых статистических характеристик рядов случайных данных:
- mean(x) – выборочное среднее значение;
- median (х) – выборочная медиана (median) – значение аргумента, которое делит гистограмму плотности вероятностей на две равные части;
- var (х) – выборочная дисперсия (variance);
- stdev(x) – среднеквадратичное (или стандартное) отклонение (standard deviation);
- max(x),min(x) – максимальное и минимальное значения выборки;
- mode(x) – наиболее часто встречающееся значение выборки;
- var(х),stdev(x) – выборочная дисперсия и среднеквадратичное отклонение в другой нормировке:
- х – вектор (или матрица) с выборкой случайных данных.
Пример использования первых четырех функций приведен в листинге 12.10.
Листинг 12.10. Расчет числовых характеристик случайного вектора:
Определение статистических характеристик случайных величин приведено в листинге 12.11 на еще одном примере обработки выборки малого объема (по пяти данным). В том же листинге иллюстрируется применение еще двух функций, которые имеют смысл дисперсии и стандартного отклонения в несколько другой нормировке. Сравнивая различные выражения, вы без труда освоите связь между встроенными функциями.
Внимание!
Осторожно относитесь к написанию первой литеры в этих функциях, особенно при обработке малых выборок (листинг 12.11).Листинг 12.11. К определению статических характеристик:
Иногда в статистике встречаются и иные функции, например, помимо арифметического среднего, применяются другие средние значения:
- gmean(x) – геометрическое среднее выборки случайных чисел;
- hmean(x) – гармоническое среднее выборки случайных чисел.
Математическое определение этих функций и пример их использования в Mathcad приведены в листинге 12.12.
Маткад как найти среднее значение функции
Встроенные функции и ключевые слова
В этом приложении дан список основных встроенных функций Mathcad. В приведенных ниже функциях для систем класса Mathcad используются следующие обозначения:
- х и у – вещественные числа;
- z – вещественное либо комплексное число;
- m, n, i, j и k – целые числа;
- v, u и все имена, начинающиеся с v – векторы;
- А и B – матрицы либо векторы;
- М и N – квадратные матрицы;
- F – вектор-функция;
- file – либо имя файла, либо файловая переменная, присоединенная к имени файла.
Все углы в тригонометрических функциях выражены в радианах. Многозначные функции и функции с комплексным аргументом всегда возвращают главное значение. Имена приведенных функций нечувствительны к шрифту, но чувствительны к регистру – их следует вводить с клавиатуры в точности, как они приведены. Все функции возвращают указанное для них значение
Как найти максимум функции в маткаде
MathCAD позволяет находить экстремумы функций, которые имеют конечное количество экстремумов. Для нахождения экстремума используются функции Minimize и Maximize .
На рис.14 показан пример использования функции нахождения минимума. Нахождение максимума происходит аналогично, за исключением того, что функцию Minimize необходимо заменить на Maximize . В данном примере показан случай, когда максимум функции не может быть найден.
8.6.1. Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис. 8.8 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканиро-вать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.
Рис. 8.8. График функции f(х)=х 4 +5х 3 -10х
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
- Minimize (f, x1, . ,хм) — вектор значений аргументов, при которых функция f достигает минимума;
- Maximize (f, х1, . ,хм) — вектор значений аргументов, при которых функция f достигает максимума;
- f (x1, . , хм. ) — функция;
- x1, . , xм — аргументы, по которым производится минимизация (максимизация).
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис. 8.8) без дополнительных условий показаны в листингах 8.11- 8.12. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.
Листинг 8.11. Минимум функции одной переменной
Листинг 8.12. Максимум функции одной переменной
Как видно из листингов, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).
1. Поиск экстремума функции
Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и (или) уравнений. В таком случае говорят о задаче на условный экстремум.
Для решения задач поиска максимума и минимума в Mathcad имеются встроенные функции Minerr, Minimize и Maximize. Все они используют те же градиентные численные методы, что и функция Find для решения уравнений.
2. Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис.2 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.
 Рис. 1. График функции f(х)=х 4 +5х 3 -10х
Рис. 1. График функции f(х)=х 4 +5х 3 -10хПостроим график заданной функции (рис.1). По графику видны участки локальных экстремумов функции.
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
· Minimize (f, x1, … ,хм) — вектор значений аргументов, при которых функция f достигает минимума;
· Maximize (f, х1, … ,хм) — вектор значений аргументов, при которых функция f достигает максимума;
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис.1) без дополнительных условий показаны в листинге на рис.2. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.


 Рис.2. Поиск локальных экстремумов функции одной переменной
Рис.2. Поиск локальных экстремумов функции одной переменнойКак видно из листинга, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются локальные различные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).
3. Условный экстремум
В задачах на условный экстремум функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. На рис.3 показаны примеры поиска условного экстремума на различных интервалах, определенных неравенствами. Сравните результаты работы этого листинга с двумя предыдущими.



Рис. 3. Три примера поиска условного экстремума функции
Не забывайте о важности выбора правильного начального приближения и в случае задач на условный экстремум. Например, если вместо условия — 3 Скачать пример
Александр Малыгин
Объект обсуждения – программное обеспечение для выполнения автоматизированного конструкторского и технологического проектирования, разработки управляющих программ, вопросы, связанные с разработкой прикладных САПР.
2 Комментарии “ Оптимизация функций одной и нескольких переменных в PTC MathCAD ”
Спасибо, очень информативано! Скажите, а для 9 переменных такая же функция и такой же принцип используется?
Функция будет другая. Вы сами подбираете вид функции, остальное аналогично.

15.3. Теоретические распределения 565
мал, то такая случайная величина распределена по логнормальному закону. Логнор мальное распределение задается, в общем, той же формулой, что и нормальное, един ственное, вместо параметров в ней используются их натуральные логарифмы:
В Mathcad характеристики этого распределения вычисляются с помощью функций, имя которых задается добавлением соответствующей приставки к корню lnorm (x,ln(a),ln(σ)).
Распределение Коши
Распределение Коши относится к имеющим лишь теоретическое значение и описыва ется плотностью
В Mathcad для задания имен функций характеристик распределения Коши использу ется корень cauchy (x,µ,λ).
Распределение Вейбулла
Это распределение также редко применяется для решения реальных проблем: может быть использовано, например, для определения времени выполнения какой либо за дачи. Распределение Вейбулла имеет следующую плотность:
В Mathcad оно прописано в виде встроенных функций, названия которых имеют об щий корень weibull(x,s).
Гамма#распределение
Теоретическое распределение с плотностью
Может применяться, например, для определения времени выполнения какой либо за дачи. В Mathcad характеристики этого распределения можно вычислить с помощью функций, имена которых образованы добавлением соответствующих приставок к кор ню gamma(x,s) (s>0 — параметр формы).
Бета#распределение
Теоретическое распределение, плотность которого определяется формулой
566 Глава 15. Теория вероятностей и математическая статистика
Задается с помощью функций, названия которых имеют общий корень beta(x,s1,s2), где s1 и s2 — положительные параметры формы. Может быть использовано как прибли женная модель в случае отсутствия данных, поскольку плотность бета распределения может принимать различные формы в зависимости от параметров s1 и s2.
Логистическое распределение
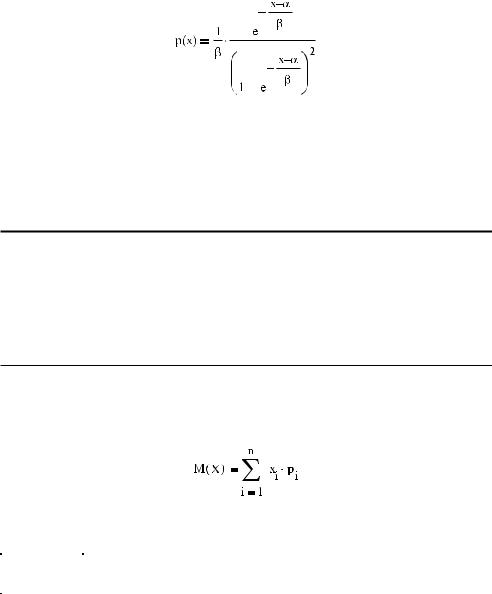
Данное распределение широко используется в экономических исследованиях. Плот ность вероятностей задается следующей формулой:
где α — среднее распределения, β — параметр.
Для задания имен функций характеристик распределения используйте соответствую щие приставки к корню logis(x,a,b). Кстати, по свойствам логистическое распределение очень схоже с нормальным.
15.4. Числовые характеристики дискретных случайных величин
В предыдущем разделе мы рассмотрели пример вычисления таких характеристик слу чайной величины, как дисперсия и математическое ожидание. Однако сделано это было за счет непосредственного задания соответствующих формул, что может быть для ряда параметров весьма неудобно по причине сложности таких формул. Значительно облегчить выполнение расчетов могут имеющиеся в Mathcad встроенные функции для вычисления практически всех используемых статистических характеристик выборки. Именно им мы и посвятим данный раздел.
15.4.1. Математическое ожидание
Одним из основных понятий статистики является понятие математического ожида ния. Если же случайная величина принимает значения с разной вероятностью, мате матическое ожидание вычисляется по формуле
Пример 15.24. Найти математическое ожидание дискретной случайной величины, закон распределения которой задан таблицей:
|
X |
1 |
2 |
3 |
4 |
5 |
|
P |
0,15 |
0,25 |
0,3 |
0,2 |
0,1 |

15.4. Числовые характеристики дискретных случайных величин 567
Решение данной задачи найти не сложно, если помнить принципы работы с векторами:
Если же случайная величина принимает ряд значений с равной вероятностью, то мате матическое ожидание определяется как среднее арифметическое значение некоторого количественного признака выборки.
В Mathcad среднее значение выборки можно подсчитать с помощью встроенной функ ции mean(x).
Пример 15.25. При измерении величины силы тока были получены следующие значения: 0.45, 0.41, 0.44, 0.42, 0.45, 0.41, 0.49, 0.56, 0.47, 0.48, 0.52, 0.43. Вычислить выборочное среднее
При обработке экспериментальных данных среднее значение выборки считается рав ным истинному значению параметра. Однако такое утверждение абсолютно верно лишь в том случае, если выборка является генеральной, то есть содержит все возмож ные значения измеряемой величины. Естественно, что реально с генеральными сово купностями работать невозможно, а всегда приходится делать из них некоторые не большие выборки. В зависимости от условий отбора и объема выборки она может быть репрезентативной в большей или меньшей степени — то есть передавать особенности генеральной совокупности с различной точностью. При этом такие характеристики, как среднее значение и дисперсия, приобретают случайный характер. Исследование особенностей поведения такого рода величин — это очень важная и сложная статисти ческая задача.
15.4.2. Дисперсия и среднеквадратичное отклонение
Встатистике дисперсией называется среднее арифметическое квадратов отклонений случайной величины от ее среднего значения:
Вобщем случае дисперсия является характеристикой степени рассеяния значений выборки по сравнению с ее средней величиной.
ВMathcad простая выборочная дисперсия вычисляется с помощью функции var(x). Кроме того, существует и функция Var(x), определяющая так называемую исправлен ную дисперсию, используемую на практике для несмещенной оценки генеральной дис персии при малом объеме выборки:

568 Глава 15. Теория вероятностей и математическая статистика
Учитывая, что функции выборочной и исправленной дисперсий отличаются лишь форматом первой буквы, к их заданию следует подходить особенно осторожно.
На практике обычно используют не саму дисперсию, а квадратный корень из нее, на зываемый среднеквадратичным отклонением. В Mathcad существуют две функции для вычисления этого параметра: stdev(x) — выборочное стандартное отклонение и Stdev(x) — исправленное среднеквадратичное отклонение.
Пример 15.26. Подбрасывается игральный кубик. Случайная величина Х — количество выпавших очков. Найти дисперсию и среднеквадратичное отклонение случайной величины Х
Абсолютно аналогичные результаты получаются и при использовании известных формул:
15.4.3. Мода и медиана
Модой в статистике называют варианту, которая встречается в выборке наиболее часто.
ВMathcad подсчитать моду выборки можно с помощью встроенной функции mode(x).
Втом случае, если все варианты встречаются в выборке с одинаковой частотой, систе ма выдаст сообщение: No value occurs more than any others (Ни одна величина не встреча ется чаще, чем все остальные).
Медианой называется варианта, которая делит вариационный ряд (проще говоря, рас сортированную выборку) на две части, равные по количеству вариант. То есть если ко личество элементов выборки нечетное и равно 2k+1, то, очевидно, медианой будет яв ляться (k+1) й элемент. В случае четного количества вариант медиана определяется как среднее арифметическое между k м и (k+1) м элементами выборки.
В Mathcad медиана вычисляется с помощью встроенной функции median(x).
Пример 15.27. Вычисление моды и медианы
Обратите внимание на то, что статистические функции могут корректно работать не толь ко с векторами столбцами, но и векторами строками.

15.4. Числовые характеристики дискретных случайных величин 569
15.4.4. Размах варьирования
Такая важнейшая характеристика рассеяния вариационного ряда, как размах варьиро вания может быть очень просто вычислена в Mathcad с помощью двух специальных матричных функций:
max(x) — возвращает максимальное значение в векторе выборки;
min(x) — функция находит минимальную величину в выборке. Используя описанные функции, размах варьирования можно задать как
Пример 15.28. Вычисление размаха варьирования
Для задания вектора выборки воспользуемся генератором случайных чисел, распределенных по показательному закону:
15.4.5. Наибольший общий делитель и наименьшее общее кратное
При решении некоторых специфических задач в статистике бывает необходимым определить, на какое максимальное целое число делятся без остатка все величины в вы борке. В Mathcad можно очень просто вычислить такое число и не создавая специаль ных алгоритмов. Для этого следует обратиться к встроенной функции gcd(x) (от англ. Greatest common divisor — наибольший общий делитель).
Схожей с описанной является задача поиска наименьшего числа, которое делится без остатка на все значения элементов выборки. В Mathcad ее можно решить с помощью встроенной функции lcm(x) (сокращение от Least common multiple — наименьшее об щее кратное).
Пример 15.29. Использование функций gcd(x) и lcm(x)
15.4.6. Геометрическое и гармоническое среднее
Чаще всего в статистике используется рассмотренное нами ранее среднее арифмети ческое количественного признака выборки. Однако в ряде специфических задач могут быть востребованы и функции, вычисляющие другие средние значения:
gmean(x) — геометрическое среднее выборки;
hmean(x) — гармоническое среднее.

570 Глава 15. Теория вероятностей и математическая статистика
Пример 15.30. Вычисление различных средних для выборки
15.5. Проверка некоторых статистических гипотез
15.5.1. Распределение Фишера. Сравнение двух дисперсий нормальных генеральных совокупностей
Отношение двух независимых случайных величин, распределенных по закону χ2, опи сывается распределением Фишера–Снедекора. На практике F критерий Фишера при меняется для проверки нулевой гипотезы о равенстве дисперсий двух генеральных совокупностей. Подобная задача возникает в том случае, если требуется сравнить точ ность приборов, инструментов или воспроизводимость результатов измерения, полу ченных различными методами. Естественно, из них стоит предпочесть тот, который дает меньшую дисперсию, то есть ошибку.
Распределение Фишера зависит только от количества степеней свободы случайных величин. Напомним, количество степеней свободы для данной выборки на единицу меньше ее объема.
На практике для проверки гипотезы обычно используют таблицы критических точек распределения Фишера–Снедекора. В том же случае, если задача решается в Mathcad, можно применить встроенную функцию квантилей qF(a,d1,d2), где a — доверительная вероятность, d1 — количество степеней свободы большей исправленной дисперсии, d2 — меньшей. Если отношение исправленных дисперсий меньше квантили распреде ления Фишера, то нулевую гипотезу о равенстве дисперсий принимают, в противном случае — отвергают.
Пример 15.31. Для сравнения точности двух станков взяты две пробы, объемы которых n1=10 и n2=8. В результате измерения контролируемого размера отобранных изделий получены следующие результаты:
|
Xi |
1,08 |
1,10 |
1,12 |
1,14 |
1,15 |
1,25 |
1,36 |
1,38 |
1,40 |
1,42 |
|
Yi |
1,11 |
1,12 |
1,18 |
1,22 |
1,33 |
1,35 |
1,36 |
1,38 |
— |
— |

15.5. Проверка некоторых статистических гипотез 571
Можно ли считать, что станки обладают одинаковой точностью, если принять уровень значимости α=0,1 и в качестве конкурирующей гипотезы D(x)≠D(y)
Задаем векторы случайных величин, объемы выборок и уровень значимости:
Вычисляем исправленные дисперсии выборок:
Определяем отношение большей исправленной дисперсии к меньшей:
Находим критическую точку Fкр, задействовав функцию квантилей qF. Для конкурирующей ги потезы D(x)≠D(y) необходимо принять вдвое уменьшенный уровень значимости.
Следовательно, нет оснований отвергать нулевую гипотезу, то есть считать точность станков различной.
15.5.2. Асимметрия и эксцесс. Проверка гипотезы о нормальном распределении
Очень часто в статистике требуется установить, является ли данное эмпирическое рас пределение нормальным, а если оно таковым не является, то с помощью какой либо количественной характеристики показать меру отклонения данного распределения от нормального. В качестве таких характеристик используются асимметрия и эксцесс. Для нормального распределения эти признаки равны нулю.
Асимметрия позволяет оценить меру отклонения функции данного распределения от центра рассеяния. Для генеральной совокупности асимметрия вычисляется с уче том исправленного среднеквадратичного отклонения (которое используется для оцен ки среднеквадратичного отклонения генеральной совокупности):
Асимметрия положительна, если вытянут правый участок кривой распределения, и от рицательна, если левый.
В Mathcad асимметрию для генеральной совокупности по данным некоторой предста вительной выборки можно подсчитать с помощью функции skew(x) (от англ. skewness — асимметрия).
Даже если асимметрия распределений одинакова, их кривые могут значительно разли чаться: одни будут иметь более высокие и острые пики, другие, наоборот, будут изме няться очень плавно. Показателем остроты пика является эксцесс.
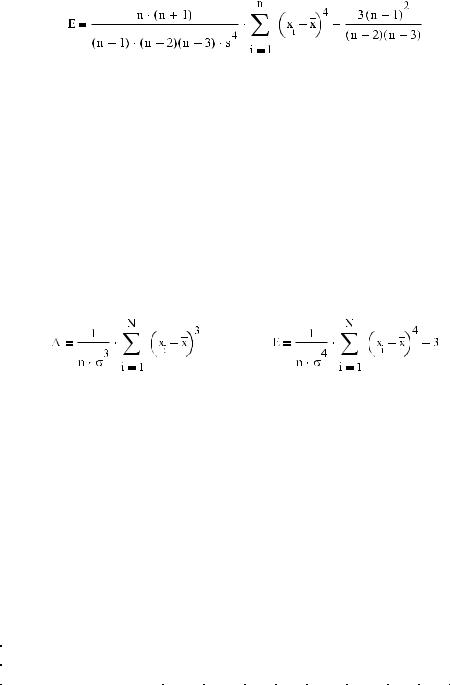
572 Глава 15. Теория вероятностей и математическая статистика
Для генеральной совокупности эксцесс рассчитывается с учетом исправленного сред неквадратичного отклонения по формуле:
Если эксцесс больше 0, то распределение имеет более острую вершину, чем нормаль ное, если же он меньше 0 — наоборот.
В Mathcad эксцесс для генеральной совокупности по данным некоторой репрезента тивной выборки можно подсчитать, используя встроенную функцию kurt(x) (от англ. kurtosis — эксцесс).
Асимметрия выборочной совокупности (не представляющей пропорции некоторой генеральной совокупности) определяется как отношение центрального момента тре тьего порядка к кубу выборочного стандартного отклонения, а ее эксцесс — соотноше нием четвертого центрального момента к четвертой степени выборочного стандартного отклонения за вычетом тройки. Но следует помнить, что для малых выборок, с кото рыми вам чаще всего приходится встречаться при решении задач, точность оценок этих параметров невысока. В принципе, сами по себе выборочные оценки асимметрии и экс цесса еще не являются показателями того, что распределение выборки соответствует нормальному закону, поэтому к ним нужно относиться с осторожностью. В учебной литературе, как правило, приводятся упрощенные формулы для определения асиммет рии или эксцесса выборки:
Воспользовавшись ими, вы почти наверняка получите результат, отличный от рассчи танного встроенными функциями skew(x) и kurt(x), поскольку Mathcad рассматривает любую выборку как репрезентативную для некоторой генеральной совокупности. По этому при вычислении данных параметров определитесь, что является для вас более важным: совпадение результата с ответом в задачнике или же максимально коррект ная количественная оценка отклонения распределения от нормального. В первом слу чае используйте привычные для вас упрощенные выражения. Со второй же проблемой функции skew(x) и kurt(x) справятся куда лучше.
В статистике асимметрия и эксцесс имеют довольно широкое применение. С их помо щью можно проверять гипотезу о нормальном распределении выборки. Например, в боль шинстве физических и химических лабораторий проверка нормальности результатов служит непременным условием полноценной аттестации используемых методик.
Пример 15.32. Рассматривая распределение размеров обуви, проданной магазином за день, как выборку из генеральной совокупности, проверить гипотезу о том, что интересующий нас признак распределен в генеральной совокупности по нормальному закону (приняв α=0,01)
|
Размер обуви, xi |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
|
Количество пар, yi |
1 |
2 |
3 |
5 |
10 |
13 |
9 |
6 |
1 |

15.5. Проверка некоторых статистических гипотез 573
Трудность, с которой вы можете столкнуться при решении задач по статистике в Mathcad, связа на с тем, что в условиях задач, как правило, выборки представлены в виде статистических рядов распределения. В Mathcad же необходимо представлять все имеющиеся данные в виде вектора, в котором каждая варианта встречается указанное количество раз. Так, в нашем примере для кор ректной работы функций skew(x) и kurt(x) нужно задать вектор размеров обуви длиной равной общему количеству проданных пар.
Формируем вариационный ряд и вектор частот:
С помощью вложенного цикла задаем вектор размеров обуви:
Теперь как длину полученного вектора определяем объем выборки, задействовав функцию length(x) (возвращает количество элементов вектора):
Если асимметрия и эксцесс превысят по модулю утроенные значения собственных среднеквад ратичных отклонений, то гипотезу о нормальности распределения следует отвергнуть. В против ном случае она должна быть принята.
Вычисляем асимметрию, эксцесс и среднеквадратичные отклонения для них:
Проверяем критерии согласия:
Требуемые условия выполняются, значит, в генеральной совокупности признак распределен по нормальному закону.

574 Глава 15. Теория вероятностей и математическая статистика
15.5.3. Проверка гипотезы о показательном распределении
Если случайная величина распределена по показательному закону, математическое ожидание и среднеквадратичное отклонение распределения должны совпадать. Это утверждение используется для проверки гипотезы о показательном распределении экспериментальных данных.
Пример 15.33. В результате испытания 200 элементов на длительность работы получено следующее эмпирическое распределение
|
Xi-Xi+1 |
0–5 |
5–10 |
10–15 |
15–20 |
20–25 |
25–30 |
|
ni |
133 |
45 |
15 |
4 |
2 |
1 |
(в первой строке указаны интервалы времени в часах, во второй — количество элементов, проработавших время в пределах соответствующего интервала). Требуется при уровне значимости 0,05 проверить гипотезу о том, что время работы элементов распределено по показательному закону
Для проверки гипотезы, как и в предыдущем примере, нам необходимо составить вектор данных, длина которого равна объему выборки. Однако в нашем случае распределение случайной вели чины задано в виде последовательности интервалов и соответствующих им частот, поэтому в ка честве «представителя» каждого интервала выберем его середину. Создадим вектор границ про межутков и путем несложного преобразования сформируем из него вектор середин интервалов:
Далее зададим вектор частот:
С помощью алгоритма, описанного в предыдущем примере, представим случайную величину в удобной для анализа в Mathcad форме, а затем оценим ее математическое ожидание и средне квадратичное отклонение:
Урок 13. Обработка статистических данных в Mathcad
В этом и последующих уроках мы будем работать со статистическими данными. Эти данные будем рассматривать как два вектора одинаковой длины, один из которых включает в себя независимые переменные, а второй — зависимые.
Выше находятся три вектора, каждый из которых включает в себя 1000 элементов. Отображены только первые несколько элементов. Чтобы просмотреть другие элементы, следует щелкнуть по трем точкам внизу столбца чисел, чтобы появился ползунок — квадрат на серой линии:
Первый вектор включает в себя независимую переменную. Вектор X содержит действительные числа, Y — нули и единицы — категории, которые служат для обозначения да/нет, орел/решка и т.п. Эти данные сгенерированы в Mathcad. Как это сделано, мы рассмотрим в конце урока.
Категории и действительные числа в статистике рассматриваются по-разному. Однако, в некоторых случаях такое разделение не совсем ясно — данные можно отнести к любой из двух групп.
Данные выше составляют генеральную совокупность из 1000 точек. В какой-то момент мы рассматривает выборку из этой генеральной совокупности. Часто мы хотим получить представление о свойствах генеральной совокупности, изучая выборку.
Описание данных
Рассмотрим сначала действительные числа. В первую очередь, для описания набора данных используются параметры:
(а) среднее арифметическое X_;
(б) среднеквадратическое (стандартное) отклонение S.
Среднее арифметическое показывает, где находится центр распределения, а среднеквадратическое отклонение (сокращенно СКО) — ширину распределения. Иногда используются и другие параметры, такие как медиана и эксцесс. Эти параметры можно найти в меню Функции -> Статистические:
Среднее арифметическое зависимой переменной X:
СКО переменной X:
Функция в Mathcad:
(В статистике среднее арифметическое обычно обозначается буквой с черточкой над ней. В Mathcadтакая черточка используется с другой целью, поэтому для обозначения среднего арифметического мы используем нижнее подчеркивание.)
Теперь рассмотрим выборку — только первые десять элементов. Условимся обозначать генеральную совокупность заглавной буквой, а выборку — маленькой:
Среднее арифметическое и СКО выборки можно использовать оценки этих же величин для генеральной совокупности:
Здесь у нас в выборке участвуют 10 элементов — такое число часто принимается за минимум выборки. Немного лучшую оценку СКО дает величина:
Здесь мы делили на (n-1) вместо n. Встроенная функция Mathcad:
Ниже находятся два графика, которые показывают некоторые характеристики распределения. Первый — это график в декартовых координатах, известный как диаграмма рассеяния. Он показывает точки данных и границы 2?:
Правило двух сигма в статистике гласит, что для нормального распределения 5% данных будут лежать вне границ 2? от среднего арифметического.
Второй график — гистограмма. Она показывает число точек данных, попавших в различные интервалы. Как его построить, мы обсудим в дальнейшем:
Различные наборы данных можно получить, нажав [Ctrl+F5]. Это займет время, поскольку пересчитывается весь документ.
Теперь рассмотрим данные категорий. Предположим, что мы рассматриваем результат подбрасывания монеты: «1» — орел, «0» — решка. Из нашего набора данных мы можем получить вероятность выпадения орла. Следует внимательно применять арифметические операции к данным категорий, но в нашем выборе между «0» и «1» мы можем легко получить долю единиц, найдя среднее арифметическое вектора Y:
Это вероятность выпадения орла. Заметьте, что считать нужно от 0 до (N-1), чтобы учесть N точек.
Для небольшой выборки ее среднее арифметическое может существенно отличаться от среднего совокупности:
Вы можете получать различные наборы данных в выборке каждый раз, нажимая [Ctrl+F5]. Попробуйте сделать это несколько раз. Для «0» и «1» нужна выборка, по крайней мере, из 30 точек, чтобы получить примерное представление о вероятности. Для надежных результатов при рассмотрении категорий нужны большие выборки — часто это тысячи точек.
Случайные числа
Данные выше были получены с использованием генераторов случайных чисел Mathcad. Они находятся в меню Функции -> Все функции -> Случайные числа. Наиболее важные из них — это равномерное и нормальное распределение.
Случайное число между 0 и x можно получить с помощью функции:
Здесь нажатие [Ctrl+F5] также даст новое значение. Чтобы получить набор случайных чисел, нужно задать диапазон:
На диаграмме рассеяния видно, что распределение действительно равномерное:
Проверим это еще раз с помощью гистограммы:
Выходными значениями функции гистограммы являются два вектора-столбца. Столбец «0» содержит центры интервалов, а столбец «1» — число элементов в каждом интервале:
При построении графика используйте тип «Столбцы»:
Получается равномерное распределение, как и ожидалось.
Случайные числа с нормальным распределением генерирует функция rnorm(). Она содержит три параметра: число точек, среднее арифметическое и СКО. Создадим набор большого числа точек:
Построим гистограмму с 30 интервалами:
Такой колоколообразный график соответствует нормальному распределению.
Резюме
- Данные включают в себя набор векторов одинаковой длины. Первый вектор — независимая переменная, второй (третий, четвертый,…) — может быть переменной категорий, или включать в себя действительные числа. Полный набор данных формирует генеральную совокупность. Любая ее часть называется выборкой.
- Поведение данных можно описать с помощью среднего арифметического и среднеквадратического отклонения. (Для категорий можно определить лишь вероятность.) В Mathcad есть функции mean() и stdev() для их вычисления. Чтобы оценить стандартное отклонение генеральной совокупности по выборке, используйте Stdev().
- Обычно одна из двадцати точек выходит за пределы границ, отстоящих по обе стороны от среднего арифметического на 2?. Это можно проверить по диаграмме рассеяния или по гистограмме. Гистограмма формируется с помощью функции histogram(intervals,x), выходом которой является матрица с двумя столбцами: столбец «0» содержит данные для оси Xграфика, столбец «1» — для оси Y. Извлечь эти столбцы по отдельности можно с помощью команды Матрицы и таблицы -> Операции с векторами/матрицами.
- Мы рассмотрели два генератора случайных чисел Mathcad. Функция rnd(3) дает случайное значение с равномерным распределением в промежутке 0
Mathcad среднее значение вектора
Глава 7. Математическая статистика
7.1 Характеристика выборки данных и связи двух массивов
MathCAD содержит 16 различных функций для оценки параметров выборки данных. Перечислим основные из них:
– mean ( A ) возвращает среднее значение элементов массива А;
– hmean ( A ) возвращает среднее гармоническое значение элементов массива А;
– gmean ( A ) возвращает среднее геометрическое значение элементов массива А;
– var ( A ) возвращает дисперсию элементов массива А;
– Var ( A ) возвращает несмещенную дисперсию элементов массива А;
– stdev ( A ) возвращает среднее квадратическое отклонение элементов массива А;
– Stdev ( A ) возвращает несмещенное среднее квадратическое отклонение элементов массива А;
– median ( A ) возвращает медиану массива А, которая делит гистограмму плотности вероятностей на две равные части;
– mode ( A ) возвращает моду массива А (наиболее часто встречающееся значение выборки данных);
– skew ( A ) возвращает ассиметрию массива А (степень ассиметричности гистограммы плотности вероятности относительно оси, проходящей через ее центр тяжести);
– kurt (х) возвращает эксцесс массив А (степень сглаженности плотности вероятности в окрестности главного максимума);
– stderr ( A , В) возвращает стандартную ошибку при линейной регрессии массивов А и В;
– cvar ( A ) возвращает ковариацию элементов двух массивов А и В;
– corr ( A ) возвращает коэффициент корреляции двух массивов А и В;
– hist ( int , y ) функция построения гистограммы массива А;
– histogram ( n , y ) функция построения гистограммы массива А.
Формулы для расчета указанных характеристик приведены на рис. 7.1 и 7.2.
Векторы наблюдений
среднее арифметическое
среднее геометрическое
среднее гармоническое
Рис. 7.1 Оценка параметров выборки данных
смещенная оценка
несмещенная оценка
среднее квадратическое отклонение
смещенная оценка
несмещенная оценка
медиана
мода
Эксцесс
ассиметрия
Рис. 7.2 Оценка параметров выборки данных (продолжение)
Все приведенные статистические функции могут использоваться для работы как с векторами, так и с матрицами. При этом статистические характеристики рассчитываются для совокупности значений всех элементов матрицы, без разделения ее на строки и столбцы. Так, для матрицы размерностью m n объем выборки равен m n .
В качестве аргументов функций можно указать любое количество векторов, матриц и скаляров. Пример вычисления статистических характеристик для нескольких массивов приведен на рис. 7.3. Порядок указания массивов не имеет значения.
В MathCAD имеются три функции для оценки связи двух векторов или матриц:
1) stderr ( A , B ) возвращает стандартную ошибку при линейной регрессии массивов А и В;
2) cvarr ( A , B ) возвращает ковариацию элементов массивов А и В;
3) corr ( A , B ) возвращает коэффициент корреляции массивов А и В.
Рис. 7.3 Оценка параметров нескольких массивов данных
Коэффициент корреляции и ковариации различаются лишь нормировкой.
Ковариация определяется по формуле
,
Коэффициент корреляции – по формуле
,
где σА, σВ – средние отклонения массивов А и В.
Чаще на практике используется коэффициент корреляции, дающий относительную, а не абсолютную (как ковариация) оценку связи двух массивов. Чем ближе к единице коэффициент корреляции, тем теснее связь. Пример расчета параметров связи массивов приведен на рис. 7.4.
Векторы наблюдений
Оценки связи двух массивов
ковариация
коэффициент корреляции
стандартная ошибка
Рис. 7.4 Оценка связи векторов А и К
Среднее значение и дисперсия
В Mathcad 11 имеется ряд встроенных функций для расчетов числовых статистических характеристик рядов случайных данных.
- mean(x) —выборочное среднее значение;
- median (х) — выборочная медиана (median) — значение аргумента, которое делит гистограмму плотности вероятностей на две равные части;
- var(x) — выборочная дисперсия (variance);
- stdev(x) — среднеквадратичное (или “стандартное”) отклонение (standard deviation);
- max(x), mm (x) — максимальное и минимальное значения выборки;
- mode(x) — наиболее часто встречающееся значение выборки;
- var (x) ,stdev(x) — выборочная дисперсия и среднеквадратичное отклонение в другой нормировке;
- х — вектор (или матрица) с выборкой случайных данных.
Пример использования первых четырех функций приведен в листинге 14.10.
Листинг 14.10. Расчет числовых характеристик случайного вектора
На рис. 14.12 приведена гистограмма выборки случайных чисел, распределенных согласно закону Вейбулла. Пунктирные вертикальные прямые, показанные на графике, рассчитаны в последней строке листинга и обозначают стандартное отклонение от среднего значения. Гистограмма получена с помощью листинга 14.8, рассмотренного в предыдущем разделе. Обратите внимание, что поскольку распределение Вейбулла, в отличие, например, от Гауссова, несимметричное, то медиана не совпадает со средним значением.
Рис. 14.12. Гистограмма распределения Вейбулла (листинг 14.10)
Определение статистических характеристик случайных величин приведено в листинге 14.11 на еще одном примере обработки выборки малого объема (по пяти данным). В том же листинге иллюстрируется применение еще двух функций, которые имеют смысл дисперсии и стандартного отклонения в несколько другой нормировке. Сравнивая различные выражения, Вы без труда освоите связь между встроенными функциями.
Осторожно относитесь к написанию первой литеры в этих функциях, особенно при обработке малых выборок (листинг 14.11).
Листинг 14.11. Копределению статических характеристик
[spoiler title=”источники:”]
http://www.math.mrsu.ru/text/courses/mcad/7.1.htm
http://bourabai.kz/einf/mathcad/ch14/index8.html
[/spoiler]
|
0 / 0 / 0 Регистрация: 10.09.2012 Сообщений: 4 |
|
|
1 |
|
Среднее геометрическое и среднее арифметическое положительных эл-ов10.09.2012, 01:05. Показов 11112. Ответов 5
программа MathCAD вычислить среднее геометрическое и арифметическое значения для положительных элементов Миниатюры
0 |
|
1074 / 655 / 68 Регистрация: 10.02.2011 Сообщений: 518 |
|
|
10.09.2012, 12:14 |
2 |
|
Попробуйте разобраться с примером на картинке: Миниатюры
2 |
|
0 / 0 / 0 Регистрация: 10.09.2012 Сообщений: 4 |
|
|
11.09.2012, 02:48 [ТС] |
3 |
|
Попробуйте разобраться с примером на картинке: не сильно помогло если чесно…буду сам разбираться. Если кому то не лень то сделайте пожалуйста и скиньте файлик маткада а не картинку, задание ведь фонарёвое
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
11.09.2012, 03:07 |
4 |
|
задание ведь фонарёвое В чём тогда проблема?
0 |
|
0 / 0 / 0 Регистрация: 10.09.2012 Сообщений: 4 |
|
|
11.09.2012, 03:42 [ТС] |
5 |
|
не будь я таким ламером, было бы всё позитивно у меня
0 |
|
vetvet |
|
11.09.2012, 17:21
|
|
Не по теме:
не будь я таким ламером, было бы всё позитивно у меня Так если вы такой ламер, то и не беритесь оценивать сложность задания, особенно если сами не в состоянии его сделать.
1 |


