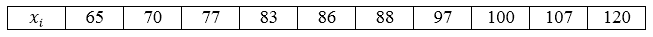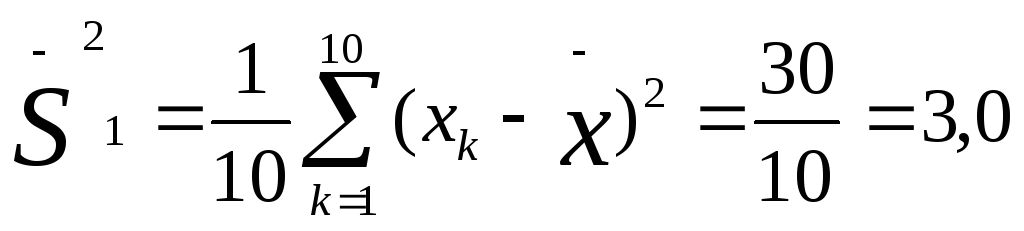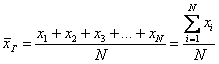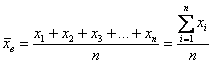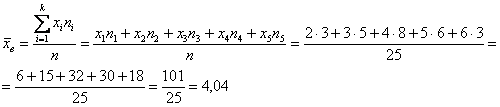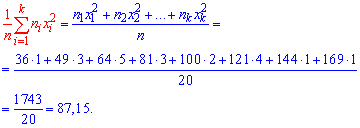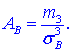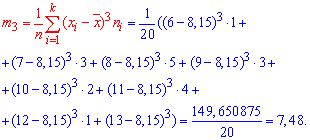Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная средняя
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная средняя — среднее арифметическое значений вариант генеральной совокупности.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная средняя вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная средняя вычисляется по формуле:
Выборочная средняя
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 3
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 4
Выборочная средняя — среднее арифметическое значений вариант выборочной совокупности.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная средняя вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная средняя вычисляется по формуле:
«Средняя выборки: генеральная, выборочная» 👇
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной средних значений за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Примеры задач на нахождение средней выборки
Пример 1
В магазин завезли 10 видов шоколадных конфет. По ним проведена следующая выборка по цене за килограмм: 70, 65, 97, 83, 120, 107, 77, 88, 100, 86. Построить ряд распределения данной генеральной совокупности и найти её генеральное среднее.
Решение.
Видим, что все значения вариант различны, поэтому частоты равны единице. Ряд распределения можно записать следующим образом, перечислив значения вариант в порядке возрастания:
Рисунок 1.
Так как наша совокупность является генеральной и все варианты различны, то мы будем пользоваться следующей формулой:
[overline{x_г}=frac{sumlimits^k_{i=1}{x_i}}{n}]
Получим:
[overline{x_г}=frac{65+70+77+83+86+88+97+100+107+120}{10}=89,3]
Ответ: 89,3.
Пример 2
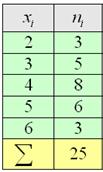
Выборочная совокупность задана следующей таблицей распределения:
Рисунок 2.
Найти среднее выборочное данной совокупности.
Решение.
Для нахождения значения выборочной средней будем пользоваться следующей формулой:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
Обычно, для наглядности и удобности вычислений составляется расчетная таблица, в которую входят необходимые промежуточные вычисления. В нашем случае составим таблицу со следующей «шапкой»:
Рисунок 3.
Внизу таблицы также добавляется строка «итог», в которой подсчитывается сумма по всем значениям столбцов. Проведя необходимые вычисления, получим следующую расчетную таблицу:
Рисунок 4.
Используя формулу, получим:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Ответ: 15,25.
Пример 3
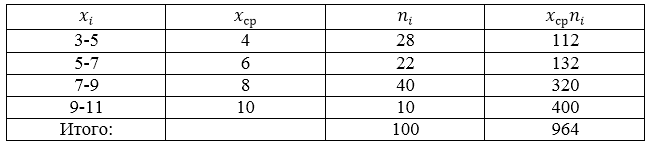
Проводится социальный опрос среди 100 пенсионеров об уровне их пенсии. Получена следующая таблица распределения результатов опроса (размер пенсии указан в тысячах рублей):
Рисунок 5.
Найти среднее выборочное данной совокупности.
Данная совокупность является выборочной, поэтому будем пользоваться следующей формулой:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
Составим, для начала, расчетную таблицу.
Рисунок 6.
Получаем:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{964}{100}=9,64]
Ответ: 9,64.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Выборочное среднее
Выборочное
среднее
значение как статистический показатель
представляет
собой среднюю оценку изучаемого в
эксперименте психологического качества.
Эта
оценка характеризует степень его
развития
в целом у той группы испытуемых, которая
была подвергнута
психодиагностическому обследованию.
Сравнивая непосредственно средние
значения двух или нескольких выборок,
мы
можем судить об относительной степени
развития у людей, составляющих эти
выборки, оцениваемого качества.
Выборочное
среднее определяется при помощи следующей
формулы:
где
хср
—выборочная
средняя величина или среднее арифметическое
значение по выборке;
п —
количество
испытуемых в выборке
или частных психодиагностических
показателей, на основе которых
вычисляется средняя величина;
xk
— частные
значения показателей
у отдельных испытуемых. Всего таких
показателей п,
поэтому
индекс k
данной
переменной принимает значения от 1 до
п;
∑ — принятый
в математике знак суммирования величин
тех
переменных, которые находятся справа
от этого знака.
Выражение
соответственно означает сумму всех х
с индексом k
от 1 до n.
Пример.
Допустим,
что в результате применения
психодиагностической
методики для оценки некоторого
психологического
свойства у десяти испытуемых мы получили
следующие частные
показатели степени развитости данного
свойства у отдельных
испытуемых: х1=
5,
х2
=
4, х3
= 5,
х4
= 6,
х5
= 7,
х6
= 3,
х7
= 6,
х8=
2,
х9=
8,
х10
=
4. Следовательно, п
= 10,
а индекс k
меняет
свои значения от 1 до 10 в приведенной
выше формуле. Для данной выборки
среднее значение1,
вычисленное по этой формуле, будет
равно:
1
В дальнейшем, как это и принято в
математической статистике, с целью
сокращения
текста мы будем опускать слова «выборочное»
и «арифметическое» и просто говорить
о «среднем» или «среднем значении».
В
психодиагностике и в экспериментальных
психолого-педагогических исследованиях
среднее,
как правило, не вычисляется
с точностью, превышающей один, два знака
после запятой, т.е.
с большей, чем десятые или сотые доли
единицы.
В
психодиагностических обследованиях
большая точность расчетов не требуется
и не имеет смысла, если принять во
внимание приблизительность тех оценок,
которые в них получаются, и достаточность
таких оценок для производства сравнительно
точных расчетов.
Дисперсия
Дисперсия
как статистическая, величина характеризует,
насколько
частные значения отклоняются от средней
величины в данной
выборке.
Чем
больше дисперсия, тем больше отклонения
или разброс данных. Прежде чем представлять
формулу для расчетов
дисперсии, рассмотрим пример. Воспользуемся
теми первичными
данными, которые были приведены ранее
и на основе которых вычислялась в
предыдущем примере средняя величина.
Мы видим, что все они разные и отличаются
не только друг от
друга, но и от средней величины. Меру их
общего отличия от средней
величины и характеризует дисперсия. Ее
определяют для того,
чтобы можно было отличать друг от друга
величины, имеющие
одинаковую среднюю, но разный разброс.
Представим
себе другую, отличную от предыдущей
выборку первичных значений,
например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко
убедиться в том, что ее средняя величина
также равна 5,0. Но в данной выборке
ее отдельные частные значения отличаются
от средней гораздо
меньше, чем в первой выборке. Выразим
степень этого отличия
при помощи дисперсии, которая определяется
по
следующей
формуле:
где
— выборочная
дисперсия, или просто дисперсия;
— выражение,
означающее, что для всех xk
от
первого
до последнего в данной выборке необходимо
вычислить разности
между частными и средними значениями,
возвести эти разности
в квадрат и просуммировать;
п —
количество
испытуемых в выборке или первичных
значений,
по которым вычисляется дисперсия.
Заметим,
что во многих изданиях дисперсию принято
обозначать как D(x).
Определим
дисперсии для двух приведенных выше
выборок частных
значений, обозначив эти дисперсии
соответственно индексами
1 и 2:
Мы
видим, что дисперсия по второй выборке
(0,4) значительно меньше дисперсии по
первой выборке (3,0). Если бы не было
дисперсии,
то мы не в состоянии были бы различить
данные выборки.
Соседние файлы в папке МатМетоды в Психологии (литература)
- #
- #
13.02.201616.87 Mб1468Наследов А.Д. IBM SPSS Statistics 20 профессиональный анализ данных.pdf
- #
3.1. Показатели центральной тенденции
Простейший пример такого показателя нам уже встречался – это среднее арифметическое значение. Но средней
дело не ограничивается, впрочем, обо всём по порядку:
3.1.1. Генеральная и выборочная средняя
Пусть исследуется некоторая генеральная совокупность объёма , а именно её числовая характеристика
, не важно, дискретная или непрерывная.
Генеральной средней называют среднее арифметическое всех значений этой совокупности:
Если среди чисел есть одинаковые (что
характерно для дискретного ряда), то формулу можно записать в более компактном
виде:
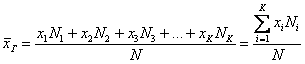
варианта повторяется
раз;
варианта –
раз;
варианта –
раз;
…
варианта –
раз.
Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду
напоминать его содержание. Далее.
Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема , и на основании исследования этой выборки делают вывод обо всей совокупности.
Выборочной средней называется среднее арифметическое всех значений выборки:
и при наличии одинаковых вариант формула запишется компактнее:
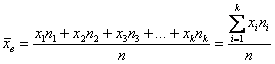
на соответствующие частоты
, делённая на объём совокупности
.
Выборочная средняя позволяет достаточно
точно оценить истинное значение , при этом, чем
больше выборка, тем точнее будет эта оценка.
Практику начнём с дискретного вариационного ряда и знакомого условия:
Пример 8
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4,
4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.
Это числа из Примера 4, но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду
и медиану.
Как решать задачу? Если нам даны первичные данные (конкретные варианты ), то их можно тупо просуммировать и разделить результат на объём
выборки:
– средний квалификационный разряд рабочих
цеха.
Но здесь удобнее составить вариационный ряд:
и использовать «цивилизованную» формулу:


| Оглавление |
Меры центральной тенденции.
До сих пор мы обсуждали методы, которые мы можем использовать для организации и представления финансовых данных с целью того, чтобы они были более понятными.
Например, частотное распределение доходности класса активов показывает характер рисков, с которыми инвесторы могут столкнуться в конкретном классе активов. Гистограмма годовой доходности S&P 500 ясно показывает, что большие положительные и отрицательные значения годовой доходности являются обычной ситуацией.
Хотя таблицы частотных распределений и гистограммы предоставляют собой удобный способ обобщить серии наблюдений, эти методы являются лишь первым шагом к описанию финансовых данных.
В этом разделе мы обсудим использование количественных показателей, которые объясняют характеристики данных. Наше внимание сосредоточено на мерах центральной тенденции и других показателях (или параметрах), характеризующих положение данных.
Показатель или мера центральной тенденции (англ. ‘measure of central tendency’) указывает, насколько центрированы финансовые данные.
Меры центральной тенденции, вероятно, используются более широко, чем любые другие статистические показатели, потому что их легко рассчитать и применить. Меры положения (англ. ‘measures of location’) включают в себя не только меры центральной тенденции, но и другие показатели, которые иллюстрируют местоположение или распространение данных в рамках распределения.
Далее мы рассмотрим общепринятые меры центральной тенденции – среднее арифметическое, медиану, моду, взвешенное среднее и среднее геометрическое. Мы также объясняем другие полезные меры положения, включая квартили, квинтили, децили и процентили.
Среднее арифметическое.
Финансовые аналитики и портфельные менеджеры часто хотят получить одно число, которое репрезентативно описывает возможный исход инвестиционного решения. Среднее арифметическое – безусловно, наиболее часто используемая мера середины или центра данных.
Определение среднего арифметического.
Среднее арифметическое (англ. ‘arithmetic mean’) – это сумма наблюдений, деленная на количество наблюдений.
Мы можем вычислить среднее арифметическое как для совокупностей, так и для выборок. Эти показатели известны как среднее по совокупности и выборочное среднее значение соответственно.
Среднее значение для совокупности.
Среднее значение для совокупности (математическое ожидание или среднее по совокупности, от англ. ‘population mean’) – это среднее арифметическое значение, рассчитанное для совокупности.
Если мы можем адекватно определить совокупность, то мы можем рассчитать среднее значение для совокупности как среднее арифметическое всех наблюдений или значений в совокупности.
Например, аналитики, изучающие годовой рост продаж крупных оптовых клубов в США за 2013 финансовый год, могут определить интересующую совокупность, включив в нее только три компании: BJ’s Wholesale Club (частная компания с 2011 г.), Costco Wholesale Corporation. и Sam’s Club, входящую в группу Wal-Mart.
Оптовый клуб (англ. ‘wholesale club’) – это формат магазина, предназначенного в основном для оптовых продаж в торговых точках размером со склад для клиентов, которые платят членские взносы. По состоянию на начало 2010-х годов эти три оптовых клуба доминировали в данном сегменте в Соединенных Штатах.
В качестве другого примера можно привести портфельного менеджера, специализирующегося на индексе Nikkei 225. Интересующая его совокупность включает 225 акций из первой секции Токийской фондовой биржи, которые формируют индекс Nikkei.
Формула среднего значения для совокупности.
Среднее по совокупности, ( bf mu), является средним арифметическим значением совокупности.
Для конечной совокупности используется следующая формула среднего значения:
(large{ mu = {dsum_{i=1}^{N}X_i over N} }) (Формула 2)
где:
- (N) – количество наблюдений во всей совокупности, а
- (X_i) – (i)-е наблюдение.
Среднее по совокупности является примером статистического параметра. Среднее значение для совокупности уникально; то есть, данная совокупность имеет только одно среднее значение.
Чтобы проиллюстрировать расчеты по приведенной формуле, мы можем найти среднее по совокупности для доли прибыли в выручке американских компаний, управляющих крупными оптовыми клубами за 2012 год.
В течение года прибыль в процентах от выручки для оптовых клубов BJ, Costco Wholesale Corporation, и Wal-Mart Stores составляли 0,9%, 1,6% и 3,5% соответственно, согласно списку Fortune 500 за 2012 год. Таким образом, среднее значение по совокупности для прибыли в процентах от выручки составило:
(mu) = (0,9 + 1,6 + 3,5)/3 = 6/3 = 2%
Выборочное среднее значение.
Среднее значение по выборке (выборочное среднее или выборочное среднее значение, от англ. ‘sample mean’) – это среднее арифметическое значение, вычисленное для выборки.
Очень часто мы не можем наблюдать каждый элемент множества данных; вместо этого мы наблюдаем подмножество или выборку из генеральной совокупности.
Концепция среднего значения может применяться к наблюдениям в выборке с небольшим изменением обозначений.
Формула выборочного среднего значения.
Выборочное среднее, ( overline{X} ) (читается как «X-bar») – это среднее арифметическое значение по выборке:
(large{ overline{X} = {dsum_{i=1}^{n}X_i over n} }) (Формула 3)
где:
- (n) – количество наблюдений в выборке.
Формула 3 предписывает суммировать значения наблюдений (X_i) и делить эту сумму на количество наблюдений. Например, если выборка коэффициентов прибыли на акцию (P/E) для шести публичных компаний содержит значения 35, 30, 22, 18, 15 и 12, то среднее значение P/E для выборки будет 132/6 = 22. Среднее значение выборки также называется средним арифметическим (англ. ‘arithmetic average’).
Статистики предпочитают использовать термин «mean», а на «average» (в русском переводе это одно и то же – «среднее»). Некоторые авторы называют все меры центральной тенденции (включая медиану и моду) термином «average». Термин «mean» позволяет избежать любой путаницы.
Как отмечалось ранее, выборочное среднее значение является статистикой (то есть описательной мерой выборки).
Средние значения можно рассчитывать для отдельных статистических единиц или для временного отрезка.
В качестве примера можно привести рентабельность собственного капитала (ROE) за 2013 год для 100 компаний из FTSE Eurotop 100, индексе 100 крупнейших компаний Европы. В этом случае мы рассчитываем среднее значение ROE за 2013 год в среднем по 100 отдельным статистическим единицам (или элементам множества, от англ. ‘statistical unit’ или просто ‘unit’).
Когда мы изучаем характеристики некоторых статистических единиц в определенный момент времени (например, ROE для FTSE Eurotop 100), мы изучаем перекрестные данные (англ. ‘cross-sectional data’). Среднее этих наблюдений называется перекрестным средним значением (англ. ‘cross-sectional mean’).
[см. также: CFA – Временные ряды и перекрестные данные]
С другой стороны, если наша выборка состоит из исторической месячной доходности по FTSE Eurotop 100 за последние 5 лет, то мы имеем дело с данными временного ряда (англ. ‘time-series data’). Среднее значение этих наблюдений называется средним временного ряда (англ. ‘time-series mean’).
Мы рассмотрим специализированные статистические методы, связанные с поведением временных рядов в следующих разделах, посвященных анализу временных рядов.
Ниже мы покажем пример определения выборочной средней доходности для 16 европейских фондовых рынков за 2012 г. В этом случае среднее значение является перекрестным, поскольку мы усредняем доходность по отдельным странам.
Пример вычисления перекрестного среднего значения.
Индекс MSCI EAFE (Европа, Австралия и Дальний Восток) – это индекс рыночной капитализации, скорректированный с учетом свободного обращения акций, предназначенный для оценки акций в развитых странах, за исключением США и Канады.
Термин «скорректированный с учетом свободного обращения акций» (англ. ‘free float-adjusted’) означает, что веса компаний в индексе отражают стоимость акций, фактически доступных для инвестиций.
По состоянию на сентябрь 2013 года EAFE состояла из 22 индексов стран развитых рынков, включая индексы для 16 европейских рынков, 2 австралийских рынков (Австралия и Новая Зеландия), 3 дальневосточных рынков (Гонконг, Япония и Сингапур) и Израиля.
Предположим, что мы заинтересованы в показателях динамики местной валюты на 16 европейских рынках EAFE в 2012 году. Мы хотим найти примерную среднюю общую доходность за 2012 год по этим 16 рынкам.
Ряды ставок доходности, представленные в Таблице 8, приведены в местной валюте (то есть доходность указана для инвесторов, проживающих в стране). Поскольку эта доходность не указывается в валюте каждого отдельного инвестора, она не является доходностью, которую мог бы получить отдельный инвестор. Это, скорее, средняя доходность для местных валют 16 стран.
|
Рынок |
Общая доходность |
|---|---|
|
Австрия |
20.72 |
|
Бельгия |
33.99 |
|
Дания |
28.09 |
|
Финляндия |
8.27 |
|
Франция |
15.90 |
|
Германия |
25.24 |
|
Греция |
-2.35 |
|
Ирландия |
2.24 |
|
Италия |
6.93 |
|
Нидерланды |
15.36 |
|
Норвегия |
6.05 |
|
Португалия |
-2.22 |
|
Испания |
-4.76 |
|
Швеция |
12.66 |
|
Швейцария |
14.83 |
|
Великобритания |
5.93 |
Источник: www.msci.com.
Используя данные Таблицы 8, рассчитайте выборочную среднюю доходность для 16 фондовых рынков за 2012 год.
Решение:
При расчете к ставкам доходности применяется Формула 3:
(20,72 + 33,99 + 28,09 + 8,27 + 15,90 + 25,24 – 2,35 + 2,24 + 6,93 + 15,36 + 6,05 – 2,22 – 4,76 + 12,66 + 14,83 + 5,93) / 16 = 186,88 / 16 = 11,68%
Мы можем убедиться, что на 8 рынках доходность была меньше среднего, а на других 8 – выше среднего. Мы не должны ожидать, что какие-либо фактические наблюдения будут равны среднему значению, потому что выборочные средние значения предоставляют только сводку анализируемых данных.
Кроме того, хотя в этом примере число значений ниже среднего равно количеству значений выше среднего, это не обязательно так на самом деле. Как финансовому аналитику, вам часто нужно будет находить несколько показателей, которые описывают характеристики распределения.
Среднее значение – это, как правило, статистика, которую вы будете использовать как показатель типичного результата для распределения. Затем вы можете использовать среднее значение для сравнения динамики двух разных рынков.
Например, вам может быть интересно сравнить показатели фондового рынка стран Азиатско-Тихоокеанского региона с показателями фондового рынка европейских стран. Вы можете использовать среднюю доходность этих рынков, чтобы сравнить результаты инвестиций.
Свойства среднего арифметического.
Среднее арифметическое можно сравнить с центром тяжести объекта. Рисунок 5 выражает эту аналогию графически и представляет собой график девять гипотетических наблюдений.
Девять наблюдений: 2, 4, 4, 6, 10, 10, 12, 12 и 12. Среднее арифметическое составляет 72/9 = 8. Наблюдения наносятся на ось как столбцы с различной высотой в зависимости от их частоты (то есть 2 – высота в одну единицу, 4 – высота в две единицы и т. д.).
Когда ось помещается на точку опоры, она сбалансируется только тогда, когда точка опоры совпадает с отметкой на оси, соответствующей среднему арифметическому значению.
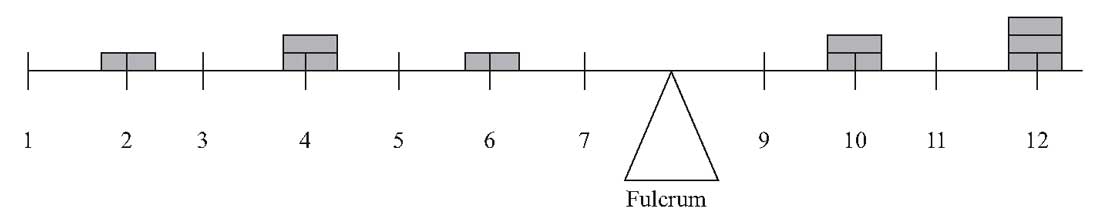
Когда точка опоры установлена на отметку 8, ось идеально сбалансирована.
Как финансовые аналитики, мы часто используем среднюю доходность как меру типичного результата для актива. Однако, как и в приведенном выше примере, некоторые результаты оказываются выше среднего, а некоторые – ниже. Мы можем рассчитать расстояние между средним значением и каждым результатом и назвать его отклонением (англ. ‘deviation’).
Математически всегда верно, что сумма отклонений от среднего равна 0. Мы можем убедиться в этом, взяв среднее арифметическое, приведенное в Формуле 3, и умножив обе части уравнения на (n):
({ noverline{X} = dsum_{i=1}^{n}X_i })
Таким образом, сумма отклонений от среднего значения может быть рассчитана следующим образом:
({ begin{align} & sum_{i=1}^{n} (X_i – overline{X}) = \ & sum_{i=1}^{n}X_i – sum_{i=1}^{n} overline{X} = \ & sum_{i=1}^{n}X_i – noverline{X} = 0 end{align} })
Отклонения от среднего арифметического являются важной информацией, поскольку они указывают на риск. Концепция отклонений от среднего значения формирует основу для более сложных понятий дисперсии, асимметрии и эксцесса, которые мы обсудим в следующих разделах.
Преимущества и недостатки среднего арифметического.
Преимущество среднего арифметического над двумя другими мерами центральной тенденции, – медианой и модой, состоит в том, что среднее использует всю информацию о размере и величине наблюдений. Со средним арифметическим также легко работать математически.
Потенциальный недостаток среднего арифметического – это его чувствительность к экстремальным значениям.
Поскольку для вычисления среднего значения используются все наблюдения, среднее арифметическое может резко увеличиваться или уменьшаться за счет чрезвычайно больших или малых наблюдений, соответственно.
Например, предположим, что мы вычисляем среднее арифметическое следующих семи чисел: 1, 2, 3, 4, 5, 6 и 1000.
Среднее значение равно 1,021 / 7 = 145,86 или приблизительно 146. Поскольку величина среднего, 146, намного больше, чем величина большинства наблюдений (первые 6), мы можем задаться вопросом, насколько хорошо она представляет положение данных в распределении.
На практике, хотя экстремальное значение (или выброс, от англ. ‘outlier’) в финансовых данных может быть редким значением в совокупности, оно также может отражать ошибку, допущенную при записи значения наблюдения или ошибку при формировании выборки из совокупности.
В частности, в последних двух случаях среднее арифметическое может вводить в заблуждение. Наиболее распространенный подход в таких случаях – использовать медиану вместо или в дополнение к среднему значению.
Медиана будет рассмотрена далее.
Другие подходы к обработке экстремальных значений включают применение вариаций среднего арифметического.
Усеченное среднее значение (от англ. ‘trimmed mean’ или ‘truncated mean’) вычисляется путем исключения указанного небольшого процента самых низких и самых высоких значений. Затем вычисляется среднее арифметическое из оставшихся значений.
Например, среднее значение, усеченное на 5%, отбрасывает наименьшие 2,5% и наибольшие 2,5% значений и вычисляет среднее из оставшихся 95% значений.
Усеченное среднее значение часто используется в спортивных соревнованиях, когда самые низкие и самые высокие оценки судей отбрасываются при подсчете оценки участника.
Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.
Индивидуальное задание 1
Вариант 11
Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моду;
- квантильное отклонение;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:
Эмпирическую функцию распределения определим по формуле
Здесь nx – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:
Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле
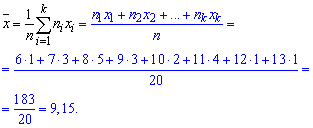
Выборочную дисперсию находим по формуле
Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу
Подправленную дисперсию вычисляем согласно формулы
Выборочное среднее квадратичное отклонение вычисляем по формуле
Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии
Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
Медиану находим по 2 формулам:
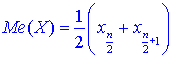
если число n – нечетное.
Здесь берем индексы в xi согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому
Мода – это варианта которая в вариационном ряду случается чаще всего, то есть
Квантильное отклонение находят по формуле
где – первый квантиль,
– третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение
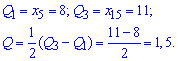
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему
Коэффициент асимметрии находим по формуле
Здесь 
Подставляем в формулу коэффициента асимметрии
Эксцессом статистического распределения выборки называется число, которое вычисляют по формуле:
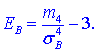
Здесь m4 центральный эмпирический момент 4-го порядка. Находим момент
а далее эксцесс
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
- Следующая статья – Построение уравнения прямой регрессии Y на X