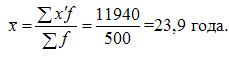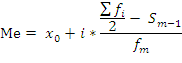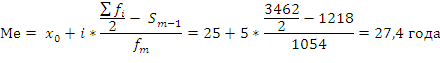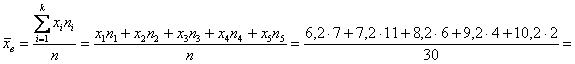Как найти среднее значения для интервального ряда

Например, средняя арифметическая для интервального ряда

При расчете средней арифметической для
интервального вариационного ряда
сначала определяют среднюю для каждого
интервала, как полусумму верхней и
нижней границ, а затем — среднюю всего
ряда. В случае открытых интервалов
значение нижнего или верхнего интервала
определяется по величине интервалов,
примыкающих к ним.

Пример
3. Определить
средний возраст студентов вечернего
отделения.

Возраст в годах	Число студентов	Среднее значение интервала	Произведение середины интервала (возраст) на число студентов
до 20	65	(18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20)	1235
20 — 22	125	(20 + 22) / 2 = 21	2625
22 — 26	190	(22 + 26) / 2 = 24	4560
26 — 30	80	(26 + 30) / 2 = 28	2240
30 и более	40	(30 + 34) / 2 = 32	1280
Итого	500		11940

Средние, вычисляемые из интервальных
рядов являются приближенными.

1. Структурные средние величины

Кроме степенных средних в статистике
для относительной характеристики
величины варьирующего признака и
характеристики рядов распределения
пользуются структурными средними: модой
и медианой.

Мода

Мода— это наиболее часто
встречающийся вариант ряда. Мода
применяется, например, при определении
размера одежды, обуви, пользующейся
наибольшим спросом у покупателей.

Модой для дискретного ряда является
варианта, обладающая наибольшей частотой.

При вычислении моды для интервального
вариационного ряда необходимо:

1. сначала определить модальный интервал
   (по максимальной частоте),

2. затем — значение модальной величины
   признака по формуле:

где:

1. —
   значение моды

2. —
   нижняя граница модального интервала

3. i —
   величина интервала

4. —
   частота модального интервала

5. —
   частота интервала, предшествующего
   модальному

6. —
   частота интервала, следующего за
   модальным

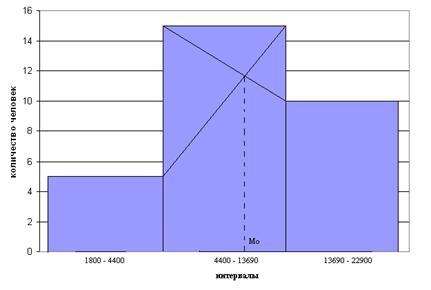
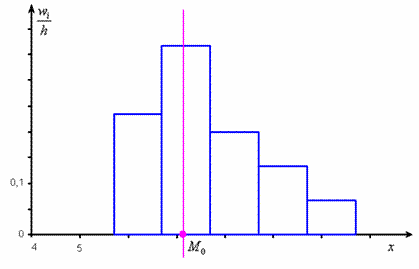
Определение моды графически:
Мода определяется по гистограмме
распределения. Для этого

правую вершину модального
прямоугольника соединяют с правым
верхним углом предыдущего прямоугольника
, а левую
вершину модального прямоугольника –
с левым верхним углом
последующего прямоугольника. Абсцисса
точки пересечения этих прямых и будет
модой распределения.

Медиана

Медиана — это значение признака,
который делит вариационный ряд на две
равные по численности части.

Медиана для дискретного ряда.

Для определения медианы в дискретном
рядус нечетнымколичеством
единиц наблюдения сначалапорядковый
номер медианыпо формуле:  ,
а затем определяют, какое значение
варианта обладает накопленной частотой,
равной номеру медианы.

Если ряд содержит четное
число элементов, то
медиана будет равна средней из двух
значений признака, находящихся в
середине. Номер первого из этих признаков
определяется по формуле: ,
для второго – .

= n
(количество элементов в ряду).

Медиана для интервального ряда

При вычислении медианы для
интервального вариационного ряда сначала
определяют медианный интервал, в пределах
которого находится медиана.

Для этого:

1. определяется номер медианы
   по формуле: ,
   полученное значение округляется до
   целого большего числа.

2. затем по
   накопленной частоте определяется
   интервал, в который входит элемент с
   таким номером,

3. затем — значение медианы по формуле:

где:

• —
  искомая медиана

• —
  нижняя граница интервала, который
  содержит медиану

• i 
   — ширина интервала

• —
  сумма частот или число членов ряда

•  –
  накопленная частота интервала,
  предшествующего медианному

• —
  частота медианного интервала

Пример.
Найти моду и медиану для интервального
ряда.

Возрастные группы	Число студентов	Сумма накопленных частот ΣS
До 20 лет	346	346
20 — 25	872	1218
25 — 30	1054	2272
30 — 35	781	3053
35 — 40	212	3265
40 — 45	121	3386
45 лет и более	76	3462
Итого	3462

Решение:

1. Определим моду

В
данном примере модальный интервал
находится в пределах возрастной группы
25-30 лет, так как на этот интервал приходится
наибольшая частота (1054).

Рассчитаем
величину моды:

Это значит, что модальный
возраст студентов равен 27 годам.

1. Определим медиану.

Медианный интервал
находится в возрастной группе 25-30 лет,
так как в пределах этого интервала
расположена варианта, которая делит
совокупность на две равные части (Σf_i/2
= 3462/2 = 1731). Далее подставляем в формулу
необходимые числовые данные и получаем
значение медианы:

Это значит, что одна половина студентов
имеет возраст до 27,4 года, а другая свыше
27,4 года.

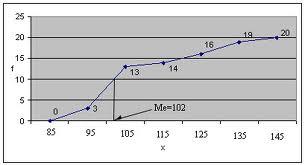
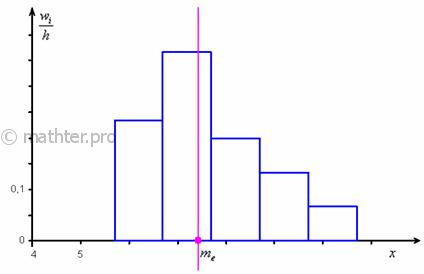
Графически медиана
определяется по кумуляте. Для ее
определения высоту наибольшей ординаты,
которая соответствует сумме всех частот,
делят пополам. Через полученную точку

проводят прямую,
параллельную оси абсцисс,
до
пересечения ее с кумулятой. Абсцисса
точки пересечения является медианой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Расчет средней величины в интервальных вариационных рядах немного отличается от расчета в рядах дискретных. Как рассчитать среднюю арифметическую и среднюю гармоническую в дискретных рядах можно посмотреть вот ЗДЕСЬ. Такое различие вполне объяснимо – это связано с особенностью интервальных рядов, в которых изучаемый признак приведен в интервале от и до.

Итак, посмотрим особенности расчета на примере.

Пример 1. Имеются данные о дневном заработке рабочих предприятия.

Дневной заработок рабочего, руб.	Число рабочих, чел.
500-1000	15
1000-1500	30
1500-2000	80
2000-2500	60
2500-3000	25
Итого	210

 Нам необходимо рассчитать среднедневную заработную плату рабочего.

Начало решения задачи будет аналогичным правилам расчета средней величины, которые можно посмотреть в этой статье.

Начинаем мы с определения варианты и частоты, поскольку ищем мы средний заработок за день, то варианта это первая колонка, а частота вторая. Данные у нас заданы явным количеством, поэтому расчет проведем по формуле средней арифметической взвешенной (так как данные приведены в табличном виде). Но на этом сходства заканчиваются и появляются новые действия.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f
500-1000	15
1000-1500	30
1500-2000	80
2000-2500	60
2500-3000	25
Итого	210

Дело в том, что интервальный рад представляет осредняемую величину в виде интервала. 500-1000, 2000-2500 и так далее. Чтобы решить эту проблему необходимо провести промежуточные действия, и только потом подсчитать среднюю величину по основной формуле.

Что же требуется в данном случае сделать. Все достаточно просто, чтобы провести расчет нам нужно, чтобы варианта была представлена одним числом, а не интервалом. Для получения такого значения находят так называемое ЦЕНТРАЛЬНОЕ ЗНАЧЕНИЕ ИНТЕРВАЛА (или середину интервала). Определяется оно путем сложение верхней и нижней границ интервала и делением на два.

Проведем необходимые расчеты и подставим данные в таблицу.

 

И так далее по всем интервалам рассчитываем центральное значение. В итоге получаем следующие результаты.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f	х’
500-1000	15	750
1000-1500	30	1250
1500-2000	80	1750
2000-2500	60	2250
2500-3000	25	2750
Итого	210	—

 После того как мы рассчитали центральные значения далее проведем расчеты в таблицы и подставим итоговые данные в формулу, аналогично тому как мы уже рассматривали ранее.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f	х’	x’f
500-1000	15	750	11250
1000-1500	30	1250	37500
1500-2000	80	1750	140000
2000-2500	60	2250	135000
2500-3000	25	2750	68750
Итого	∑f = 210	—	∑ x’f = 392500

В итоге получаем, что среднедневная заработная плата одного рабочего составляет 1869 рублей.

Это пример решения, если интервальный ряд представлен со всеми закрытыми интервалами. Но достаточно часто бывает, когда два интервала открытые, первый и последний. В таких ситуациях прямой расчет центрального значения невозможен, но есть два варианта как это сделать.

 Пример 2. Имеются данные о продолжительности производственного стажа персонала предприятия. Рассчитать среднюю продолжительность стада одного сотрудника.

Длительность производственного стажа, лет	Число сотрудников, человек
до 3	19
3-6	21
6-9	15
9-12	10
12 и более	5
Итого	70

В данном случае принцип решения останется точно таким же. Единственно, что поменялось в этой задаче, так это первый и последний интервалы. До 3 лет и 12 лет и более это и есть те самые открытые интервалы. Именно тут возникнет вопрос, а как же найти центральное значение интервала для таких интервалов.

Поступить в этой ситуации можно двумя способами:

1. Предположить какой бы мог быть интервал, учитывая, что нам приведены интервалы равные, то это вполне возможно. Интервал до 3 мог бы выглядеть как 0-3, и тогда его центральное значение будет (0+3)/2 = 1,5 года. Интервал 12 и более мог бы выглядеть как 12-15, и тогда его центральное значение было бы (12+15)/2 = 13,5 года. Все оставшиеся центральные значения интервала рассчитываются аналогично. В результате получаем следующее.

Длительность производственного стажа, лет х	Число сотрудников, человек f	х’	x’f
до 3	19	1,5	28,5
3-6	21	4,5	94,5
6-9	15	7,5	112,5
9-12	10	10,5	105,0
12 и более	5	13,5	67,5
Итого	∑f = 70	—	∑ x’f = 408,0

 

Средняя продолжительность стажа 5,83 года.

1. Принять за центральное значение, то данное которое имеется в интервале, без дополнительных расчетов. В нашем случае в интервале до 3 это будет 3, а в интервале 12 и более это будет 12. Такой способ больше подходит для ситуаций, когда интервалы неравные и предположить какой интервал мог бы быть сложно. Рассчитаем нашу задачу по таким данным далее.

Длительность производственного стажа, лет х	Число сотрудников, человек f	х’	x’f
до 3	19	3	57,0
3-6	21	4,5	94,5
6-9	15	7,5	112,5
9-12	10	10,5	105,0
12 и более	5	12	60,0
Итого	∑f = 70	—	∑ x’f = 429,0

 

Средняя продолжительность стажа 6,13 года.

Домашнее задание

1. Рассчитать средний размер посевной площади на одно фермерское хозяйство по следующим данным.

Размер посевной площади, га	Количество фермерских хозяйств
0-20	64
20-40	58
40-60	32
60-80	21
80-100	12
Итого	187

1. Рассчитайте средний возраст работника предприятия по следующим данным

Возраст персонала, лет	Число сотрудников, человек
до 18	7
18-25	68
25-40	79
40-55	57
55 и старше	31
Итого	242

Теперь Вы умеете рассчитывать среднюю в интервальном вариационном ряду!



3.1.4. Как вычислить среднюю, моду и медиану интервального ряда?

Начнём опять с ситуации, когда нам даны первичные статические данные:

Пример 10

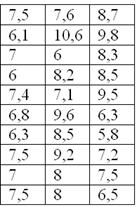
По результатам выборочного исследования цен на ботинки в магазинах города получены следующие данные (ден. ед.):

– это в точности числа из Примера 6.  Но теперь нам нужно найти среднюю, моду и медиану.

Решение: чтобы найти среднюю по первичным данным, нужно

просуммировать все варианты и разделить полученный результат на объём совокупности:
 ден. ед.

Эти подсчёты, кстати, займут не так много времени и при использовании оффлайн калькулятора. Но если есть Эксель, то,

конечно, забиваем в любую свободную ячейку:
=СУММ(, выделяем мышкой все числа, закрываем скобку ), ставим знак деления /, вводим число 30 и жмём Enter. Готово.

Что касается моды, то её оценка по исходным данным, становится непригодна. Хоть мы и видим среди чисел

одинаковые, но среди них запросто может найтись так 5-6-7 вариант с одинаковой максимальной частотой, например, частотой 2.

Поэтому модальное значение рассчитывается по сформированному интервальному ряду (см. ниже).

Чего не скажешь о медиане: забиваем в Эксель  =МЕДИАНА(, выделяем мышью все числа, закрываем

скобку ) и жмём Enter: . Причём, здесь даже ничего

не нужно сортировать.

Но в Примере 6 я проводил сортировку совокупности по возрастанию (вспоминаем и сортируем), и это хорошая возможность

повторить формальный алгоритм отыскания медианы.

Делим объём выборки пополам:
, и поскольку она состоит из чётного

количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного

ряда:
 ден. ед.

Ситуация вторая. Когда даны не первичные данные, а готовый интервальный ряд (что в учебных задачах бывает чаще).

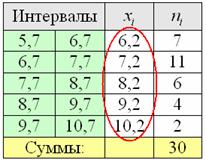
Продолжаем анализировать этот же пример с ботинками, где по исходным данным был составлен ИВР. Для вычисления средней потребуются середины  интервалов:

– чтобы воспользоваться знакомой формулой дискретного случая:

 – и это отличный результат! Расхождение с

более точным значением (), вычисленным по

первичным данным, составило всего 0,04!

Здесь мы использовали упомянутый ранее приём – приблизили интервальный ряд дискретным, и это приближение оказалось

весьма эффективным. Впрочем, с современными программами не составляет особого труда вычислить точное значение даже по

очень большому массиву первичных данных. Если они нам известны 😉

С другими центральными показателями всё занятнее.

Чтобы найти моду, нужно найти модальный интервал (с максимальной частотой) – в нашей задаче

это интервал  с частотой 11, и воспользоваться

следующей страшненькой формулой:

, где:

 – нижняя граница модального интервала;
 – длина модального интервала;
 – частота модального интервала;
 – частота предыдущего интервала;
 – частота следующего интервала.

Таким образом:
 ден. ед. – как видите, «модная» цена на

ботинки заметно отличается от среднего арифметического значения .

Не вдаваясь в геометрию формулы, просто приведу гистограмму относительных частот

и отмечу :

откуда хорошо видно, что мода смещена относительно центра модального интервала в сторону левого интервала

с бОльшей частотой. По той причине, что дешёвых ботинок больше. И, возможно, они тоже вполне себе модные.

Справочно остановлюсь на редких случаях:
– если модальный интервал крайний, то  либо ;
– если обнаружатся два смежных модальных интервала, например,  и ,

то рассматриваем модальный интервал , при этом

близлежащие интервалы (слева и справа) по возможности тоже укрупняем в два раза;
– если между модальными интервалами есть расстояние, то применяем формулу к каждому интервалу, получая тем самым две

или бОльшее количество мод.

Вот такой вот депеш мод 🙂

И медиана. Она рассчитывается чуть по менее страшной формуле. Для её применения

нужно найти медианный интервал – это интервал, содержащий варианту (либо 2 варианты), которая делит вариационный ряд на две

равные части.

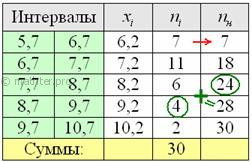
Выше я рассказал, как определить медиану, ориентируясь на относительные накопленные частоты

,  здесь же сподручнее рассчитать

«обычные» накопленные частоты . Вычислительный

алгоритм такой же – первое значение сносим слева (красная стрелка), а каждое следующее получается как сумма

предыдущего с текущей частотой из левого столбца (зелёные обозначения в качестве примера):

Всем понятен смысл чисел в правом столбце? – это количество вариант, которые успели «накопится» на всех «пройденных»

интервалах, включая текущий.
Поскольку у нас чётное количество вариант (30 штук), то медианным будет тот интервал, который содержит -ю и 16-ю варианту. И ориентируясь по накопленным частотам, легко

прийти к выводу, что эти варианты содержатся в интервале .

Формула медианы:

, где:

 – объём статистической совокупности;
 – нижняя граница медианного

интервала;
 – длина медианного интервала;
 – частота медианного интервала;
 – накопленная частота

предыдущего интервала.

Таким образом:
 ден. ед. – заметим, что медианное

значение, в отличие от моды, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант:

Справочно особые случаи:
– если медианным является крайний левый интервал, то ;
– если вариационный ряд содержит чётное количество вариант и две средние варианты попали в разные интервалы, то

объединяем эти интервалы, и по возможности удваиваем предыдущий интервал.

Ответ:  ден. ед.

По сравнению с предыдущей задачей ,

центральные показатели оказались заметно отличны друг от друга. Это говорит об асимметрии

(«скошенности») распределения цен, что хорошо видно по гистограмме и совершенно логично –

ботинок низкого и среднего ценового сегмента много, а премиального – мало.

Задание для тренировки:

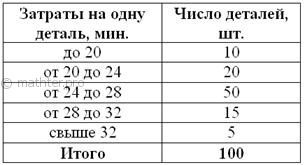
Пример 11

Для изучения затрат времени на изготовление одной детали рабочими завода проведена выборка, в результате которой получено

следующее статистическое распределение:

…да, тот самый завод Петровского 🙂 Найти среднюю, моду и медиану.

Решаем эту задачу в Экселе – все числа и инструкции уже там. Если нет Экселя, считаем на

калькуляторе, что в данном случае может оказаться даже удобнее. Образец решения, как обычно, в конце книги. Это, кстати, уже

каноничная «интервальная» задача, в которой исследуется непрерывная величина – время.

Что ещё можно сказать по теме?

Несмотря на разнообразия рассмотренных показателей, их всё равно бывает не достаточно. Существуют крайне неоднородные

совокупности, у которых варианты «кучкуются» во многих местах, и по этой причине средняя, мода и

медиана плохо характеризуют положение дел.

В таких случаях вариационный ряд дробят с помощью квартилей, децилей, а в упоротых специализированных исследованиях – и с

помощью перцентилей.

Квартили упорядоченного вариационного ряда – это варианты , которые делят его на 4 равные (по количеству вариант) части. Из чего

автоматически следует, что 2-я квартиль – есть в точности медиана: .

В тяжёлых случаях проводится разбиение на 10 частей – децилями  – это варианты, который делят упорядоченный вариационный ряд на 10 равных (по

количеству вариант) частей.

И в очень тяжелых случаях в ход пускается 99 перцентилей .

После разбиения вариационного ряда каждый участок исследуется по отдельности – рассчитываются локальные средние и другие

показатели.

В учебном курсе квартили, децили, перцентили встречаются редко, и посему я оставляю этот материал (их нахождение) для

самостоятельного изучения.

Ну а сейчас мы переходим к изучению второй группы статистических показателей:

3.2. Показатели вариации

3.1.3. Медиана

| Оглавление |



Средняя хронологическая

Краткая теория

---

Средняя хронологическая – это средний
уровень ряда динамики, т. е. средняя, исчисленная по совокупности значений
показателя в разные моменты или периоды времени. В зависимости от вида ряда
динамики применяются различные способы ее расчета, а именно расчет средней
хронологической интервального ряда и средней хронологической моментного ряда.

Ряды динамики состоят из числовых значений двух показателей:
моментов или периодов времени t, к которым относятся приводимые данные, и
соответствующих им статистических данных у, которые называются уровнями
динамического ряда. В зависимости от того, к моментам или периодам времени
привязываются статистические данные, различают два вида рядов динамики:
моментные и интервальные.

Когда уровни ряда динамики характеризуют размеры общественных
явлений за определенные интервалы (периоды) времени (за сутки, месяц, квартал,
год и т. п.), то такие ряды называются интервальными (или периодическими). В
отличие от моментного ряда динамики уровни интервального ряда динамики могут
быть суммированы. Например, сложив данные выпуска станков за четыре квартала,
можно получить показатель их выпуска за год.

Для интервальных рядов с равноотстоящими уровнями  средняя
хронологическая имеет вид средней арифметической простой:

где

 – уровни интервального ряда

 –  количество равных периодов времени

В интервальных рядах с неравноотстоящими
уровнями средняя хронологическая имеет вид средней
арифметической взвешенной:

где

 – периоды времени, отделяющие один уровень
ряда от другого

Если уровни ряда динамики выражают состояние явления на
определенные моменты времени или даты, то такие ряды называют моментными рядами
динамики. Особенность моментного ряда динамики в том, что некоторые его уровни
содержат элементы повторного счета, т. е. каждый последующий уровень полностью
или частично включает в себя предыдущий уровень. Поэтому суммирование уровней
моментного динамического ряда не имеет смысла, но разность уровней имеет
определенное значение.

В моментном ряду динамики с равноотстоящими уровнями средняя хронологическая
имеет вид:

Средний уровень моментного ряда динамики с неравноотстоящими
уровнями характеризует средняя хронологическая взвешенная, которая исчисляется
по формуле:

где

 и

 – значение уровня моментного ряда динамики и
уровня, следующего за ним;

 –
промежуток времени между датами.

Примеры решения задач

---

Задача 1

Остатки
готовой продукции на складе составили, тыс.руб.:

Дата	Остатки готовой продукции, тыс.руб.
01.04.2011	506
01.05.2011	519
01.06.2011	587
01.07.2011	624
01.08.2011	624
01.09.2011	545
01.10.2011	580
01.11.2011	542
01.12.2011	576
01.01.2012	606

Требуется:
Определить   средние остатки готовой
продукции на складе за II квартал, за III квартал, за IV квартал, за второе
полугодие 2011 года.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Средние
остатки продукции можно вычислить по формуле средней хронологической, так как
нам дан динамический моментный ряд с
равноотстоящими интервалами.

Средние
остатки за 2-й квартал:

Средние
остатки за 3-й квартал:

Средние
остатки за 4-й квартал:

Средние
остатки готовой продукции за второе полугодие:

Вывод

Таким
образом средние остатки готовой продукции за 2-й
квартал составили 557 тыс.р., за 3-й квартал 590,3 тыс.р., а за 4-й квартал 570,3 тыс.р.
Средние остатки готовой продукции за 2-е полугодие составили 580,3 тыс.р.

---

Задача 2

Известны
следующие данные об изменениях в списочном составе работников банка за январь,
человек.

	Число сотрудников
Состояло по списку на 1 января	205
на 9 января	200
на 12 января	198
на 16 января	201
на 19 января	197
на 27 января	199
Состояло по списку на 1 февраля	199

Определите
среднюю списочную численность работников банка в январе.

Решение

Данный
динамический ряд моментный, с неравноотстоящими датами.

Средняя
хронологическая взвешенная:

Вывод

Среднесписочная
численность работников банка в январе составила 200,2 чел.

---

Задача 3

Имеются
следующие данные о производстве молока в России за 1995-2000 годы  (млн.т.)

1995	1996	1997	1998	1999	2000
39.2	35.8	34.1	33.3	32.3	32.3

Для
анализа ряда динамики определите средний уровень ряда динамики.

Решение

Так
как данный динамический ряд интервальный,
с равноотстоящими уровнями, то средний уровень исследуемого динамического
ряда найдем по формуле средней арифметической:

Вывод

Среднегодовое
производство молока в исследуемом периоде составило 34,5 млн. тонн.

---

Задача 4

Имеются
следующие данные о производстве продукции на заводе (млн. руб.)

2005	2008	2010	2011	2013	2014
45,4	48,3	41,5	39,6	42,5	46,8

Для
анализа ряда динамики определите средний уровень ряда динамики.

Решение

Так
как данный динамический ряд интервальный,
с неравноотстоящими уровнями, то средний уровень
исследуемого динамического ряда найдем по формуле средней арифметической
взвешенной:

Вывод

Среднегодовое производство продукции на предприятии в исследуемом
периоде составило 44,8 млн. рублей.