Схема замещения линии электропередачи — это представление линии электропередачи в виде математической модели для исследования различных режимов работы электрической сети.
Содержание
- 1 Общие положения
- 2 Воздушная линия электропередачи
- 3 Кабельная линия электропередачи
- 4 Схема замещения с сосредоточенными параметрами
- 5 Литература
- 6 Использованные источники
Общие положения
Активное сопротивление проводов и кабелей определяется материалом токоведущих жил, их сечением и частотой электрического тока. Для большинства расчётных задач зависимостью активного сопротивления провода от частоты переменного тока пренебрегают, вследствие низкой частоты тока в электрической сети (в России 50 Гц). Эта зависимость обусловлена наличием скин эффекта.
Активное сопротивление проводников электрического тока изменяется при их нагреве или охлаждении. При этом температура проводников изменяется при изменении величины протекающего электрического тока (более подробно можно ознакомиться здесь). Вследствие этого величины удельных активных сопротивлений являются переменными величинами, и определение их по справочным таблицам позволяет получить лишь приближённую оценку их величины. Зачастую этого приближения вполне достаточно, так как оно лежит в пределах точности задания других параметров электрической сети.
Магнитное поле, возникающее вокруг и внутри проводников, определяет их индуктивное сопротивление. Электродвижущая сила (э.д.с.), соответствующая индуктивному сопротивлению наводится в каждом проводнике линии электропередачи от проводов всех фаз. Поэтому её величина, а следовательно, и величина пропорционального её индуктивного сопротивления зависят от взаимного расположения проводов. Если это расположение обеспечивает одинаковое потокосцепление каждого провода, то наводимые в проводах э.д.с. становятся равными, а индуктивные сопротивления фазных проводов линии электропередачи одинаковыми. Такое равенство имеет место при расположении фазных проводов по вершинам равностороннего треугольника.
Индуктивные сопротивления фазных проводов линии электропередачи, у которой провода расположены горизонтально, по всей длине, отличаются друг от друга. Чтобы избежать появления нежелательной нессиметрии фазных значений сопротивлений, а следовательно токов и напряжений, применяют транспозицию проводов.
В большинстве случаев можно принять, что активное и реактивное сопротивление, активная и ёмкостная проводимости равномерно распределены по всей её длине. Для линий электропередач небольшой длины (при частоте 50 Гц границей можно считать длину 300 км) распределёность параметров можно не учитывать и можно использовать более простое представление в виде схемы замещения с сосредоточенными параметрами. Обычно в расчётах режимов работы энергосистем применяется П-образная схема замещения линии электропередач с сосредоточенными параметрами.
Воздушная линия электропередачи
Расчеты параметров приведены для одной цепи ЛЭП.
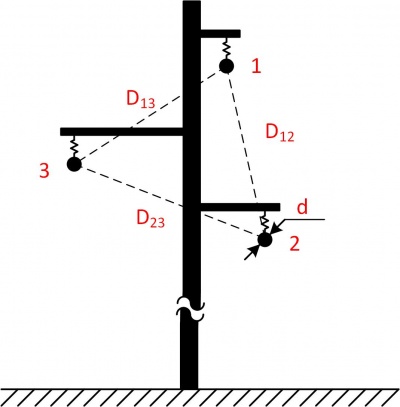
Рисунок — Пример треугольного расположения фазных проводов без расщепления на одноцепной опоре.
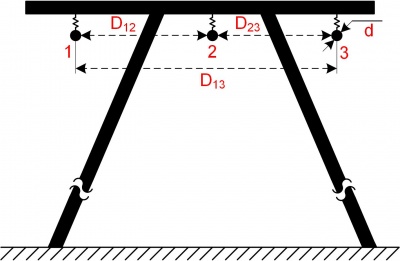
Рисунок — Пример горизонтального расположения фазных проводов без расщепления на одноцепной опоре.
Величина активного сопротивления воздушной линии электропередачи влияет на нагрев проводов, при протекании по ним электрического тока. Для сталеалюминиевых проводов, являющихся наиболее часто используемыми для воздушных ЛЭП, активное сопротивление определяется главным образом алюминиевой частью. Это обусловлено эффектом вытеснения переменного тока к поверхности проводника (скин-эфффект). Активное сопротивление в первую очередь зависит от материала, из которого изготовлен проводник, его длины и сечения. При расчётах режимов работы энергосистемы активное сопротивление принято измерять в [Ом]:
- [math]displaystyle
R = rho frac{L}{F},
[/math]
где [math]displaystyle rho[/math] — удельное активное сопротивление проводника [[math]displaystyle frac{text{Ом} cdot text{мм}^2}{text{км}} [/math]]; [math]L[/math] — длина проводника [км]; [math]F[/math] — площадь поперечного сечения проводника [[math]displaystyle text{мм}^2 [/math]].
Для сталеалюминиевых проводов (обозначение марки провода — АС), выполненных в виде стального многопроволочного сердечника и многопроволочной алюминиевой оболочки, из-за поверхностного эффекта и разницы в удельных сопротивлениях стали и алюминия практически весь ток протекает по алюминиевым проводникам. Если учесть также, что ток протекает по отдельным проводникам, навитым вокруг сердечника и имеющим длину на 3—4 % больше длины провода, то расчётное удельное сопротивление сталеалюминиевого провода, отнесенное к единице его длины, составит [math]displaystyle rho = 31,5 frac{text{Ом} cdot text{мм}^2}{text{км}}[/math].
Обычно в справочных материалах приводится удельное (погонное) сопротивление линии электропередачи [math]displaystyle R_0[/math] [Ом/км] для стандартных сечений, тогда результирующее сопротивление одного провода определяется как,
- [math]displaystyle
R = R_0 cdot L.
[/math]
Справочные значения приводятся для температуры окружающей среды 20°С. Активное сопротивление зависит от температуры, но при расчётах эта зависимость учитывается не всегда.
Индуктивное сопротивление воздушной ЛЭП определяется индуктивностью фаз ЛЭП по отношению к земле и взаимоиндукцией между фазами и, следовательно, зависит от взаимного расположения фаз, расстояния между фазами и диаметра провода.
Для устранения разницы в величине индуктивного сопротивления фаз (крайних и средней) производится транспозиция проводов.
Расположение проводов воздушной линии электропередачи на опоре может быть горизонтальным или треугольным.
Удельное индуктивное сопротивление фазы одноцепной транспонированной линии подсчитывается с учётом взаимоиндукции фаз по соотношению:
- [math]displaystyle
X_0 =0,1445 cdot lg frac{D_text{ср}}{r_{text{э}}} + frac{0,0157}{m}text{ }frac{text{Ом}}{text{км}}.
[/math]
где [math]displaystyle D_text{ср}[/math] — среднегеометрическое расстояние между фазами [м]; [math]displaystyle r_{text{э}}[/math] — эквивалентный радиус фазы, если нет расщепления то [math]displaystyle r_{text{э}}=r[/math] [м]; [math]r[/math] – радиус провода фазы [м]; [math]m[/math] — число проводов в фазе, если нет расщепления то [math]displaystyle m=1[/math] [шт.];
- [math]displaystyle
D_text{ср} =sqrt[3]{D_{1,2}D_{1,3}D_{2,3}};
[/math]
- [math]displaystyle
r_{text{э}} =sqrt[m]{r prod^m_{i=2}a_{1i} },
[/math]
где [math]displaystyle a_i[/math] — расстояние между первым и [math]displaystyle i[/math]-м проводом в фазе [м]; [math]displaystyle r = frac{d}{2}[/math] — радиус фазного проводника.
| Класс напряжения, кВ | 35 | 110 | 150 | 220 | 330 | 500 | 750 |
|---|---|---|---|---|---|---|---|
| Среднее геометрическое расстояние, м | 3,5 | 5,0 | 6,5 | 8,0 | 11,0 | 14,0 | 19,5 |
Удельная активная проводимость воздушной линии (характеризующая потери на корону крайне малый ток утечки через изоляторы) определяется по соотношению:
- [math]displaystyle
G_0 = frac{Delta P_{к.0}}{U^2_text{ном}},
[/math]
Эквивалентная активная проводимость определяется следующим образом:
- [math]displaystyle
G = G_0 cdot L.
[/math]
Для воздушных линий погонные потери активной мощности на корону существенно зависят от погодных условий и напряжения, поэтому активная погонная проводимость является переменным и нелинейным параметром. В большинстве случаев более целесообразно непосредственно учитывать для линии электропередачи в виде дополнительной нагрузки по концам линии (узлы 1 и 2) [math]displaystyle P_1=P_2=frac{Delta P_{к.0}}{2}[/math] или в виде активной проводимости на землю [math]displaystyle frac{G}{2} [/math].
Коронирование проводов приводит:
- к снижению КПД передачи электрической энергии;
- к усиленному окислению поверхности проводов;
- к появлению радиопомех.
Ёмкостная проводимость линии определяется токами смещения за счёт электростатического поля линии (между фазами и по отношению к земле). Эта проводимость создает так называемый зарядный, или ёмкостный, ток, вектор которого опережает на 90° вектор напряжения линии. Величина удельной ёмкостной проводимости
- [math]displaystyle
B_0 = frac{7,58}{lg frac{D_text{ср}}{r_{text{э}} }} cdot 10^{-6} [frac{text{См}}{text{км}}].
[/math]
Эквивалентная ёмкостная проводимость:
- [math]displaystyle
B = B_0 cdot L.
[/math]
Ёмкостная проводимость воздушных линий электропередачи слабо зависит от конструктивных особенностей ЛЭП и имеет значение от [math]2,55 cdot 10^{-6}[/math] до [math]2,80 cdot 10^{-6}[/math] [См/км] для ВЛ 110—220 кВ и от [math]displaystyle 3,4 cdot 10^{-6}[/math] до [math]displaystyle 4,2 cdot 10^{-6}[/math] [См/км] для ВЛ 330—750 кВ. Значения удельных проводимостей приводятся в справочной литературе[1].
Кабельная линия электропередачи
Кабельные линии электропередач в расчётах представляют такой же П-образной схемой замещения, что и воздушные линии. Удельные продольные активные и реактивные сопротивления определяются по справочным таблицам так же как и для воздушных линий.
Особенностью кабельных линий электропередач является близкое расположение фаз (по сравнению с воздушными линиями), что приводит к снижению удельного индуктивного сопротивления и увеличению удельной ёмкостной проводимости.
Для кабельных линий электропередачи напряжением 110 кВ и выше необходимо учитывать потери в изоляции кабеля. Они определяются по формуле:
- [math]
G = B cdot operatorname{tg} delta.
[/math]
Параметр [math]operatorname{tg} delta[/math] называется тангенс диэлектрчиеских потерь и определяется по данным завода изготовителя кабеля. Обычно находится в пределах от 0,003 до 0,006.
Схема замещения с сосредоточенными параметрами
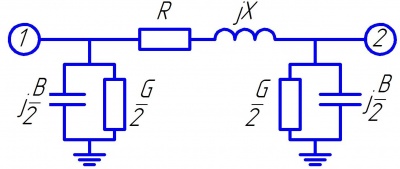
Рисунок — Полная П-образная схема замещения линии электропередачи. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.
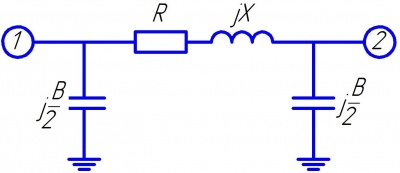
Рисунок — П-образная схема замещения линии электропередачи, только с ёмкостной проводимостью. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.

Рисунок — П-образная схема замещения линии электропередачи, без учёта шунтов. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.
При расчёте режима работы электрической сети воздушная трехфазная линия переменного тока напряжением до 500 кВ и длиной до 300 км может быть представлена схемой замещения с сосредоточенными параметрами П-образного вида. В случае превышения длины линии электропередачи 300 км необходимо изменить схему замещения одним из трёх способов:
- Разделить её на сегменты длиной менее 300 км.
- Представить линию волновыми параметрами.
- При длинах от 300 до 500 км можно использовать поправочные коэффициенты, значение которых при малых длинах близко к единице:
- [math]displaystyle K_R = 1 – frac{L^2}{3} X_0 B_0 [/math];
- [math]displaystyle K_X = 1 – frac{L^2}{6} X_0 B_0 (1 – frac{R^2_0}{X^2_0}) [/math];
- [math]displaystyle K_C = frac{3 + K_R}{2(1+K_R)}[/math].
В зависимости от класснапряжения воздушной ЛЭП можно использовать различные схемы замещения:
- 220 кВ и выше. Полная схема замещения с активным и ёмкостным шунтом.
- от 35 кВ до 220 кВ. Сокращённая схема замещения только с ёмкостным шунтом.
- до 35 кВ. Схема замещения без шунтов.
Для расчёта режимов электрической сети, как правило, используется П-образная схема замещения сети, параметры схемы замещения вычисляются для одной фазы. При расчётах режима удобно схемы замещения представлять в виде, представленном на рисунке.
Полное продольное сопротивление и проводимости (шунты узлов 1 и 2) схемы замещения имеют вид
- [math]displaystyle
Z = R +jX;
[/math]
- [math]displaystyle
Y_1 = Y_2 = frac{G}{2}+jfrac{B}{2}.
[/math]
Зачастую при расчётах установившихся режимов активная проводимость ЛЭП не учитывается, так как принятые меры борьбы с короной достаточно эффективны и, следовательно, потери на корону достаточно малы. Для воздушных линий классом напряжения менее 220 кВ потери на коронирование можно не учитывать, так как это существенно не скажется на полученной оценке параметров установившегося режима.
В случае исследования режимов воздушных линий напряжением менее 35 кВ можно не учитывать также ёмкостные шунты. В этом случае, схема замещения будет содержать только продольное сопротивление [math]Z[/math].
Литература
- Электрические системы. Электрические сети. / Под ред. д.т. н. В. А. Веникова. М.: Высшая школа — 1971.
Использованные источники
- ↑ 1,0 1,1 Справочник по проектированию электроэнергетических систем. Третье издание, переработанное и дополненное. Под редакцией С. С. Рокотяна, И. М. Шапиро. Авторы В. В. Ершевич, А. Н. Зейлигер, Г. А. Илларионов, Л. Я. Рудых, Д. Л. Файбисович, Р. М. Фришберг, Л. Д. Хабачев. И. М. Шапиро. М.: Энергоатомиздат, 1985
В данной статье будет рассматриваться пример определения индуктивного сопротивления воздушной линии 10 кВ.
Пример
Требуется определить индуктивное сопротивление воздушной линии 10 кВ со сталеалюминиевыми проводами марки АС-50/8,0, длина линии составляет 5 км, используется промежуточная опора П10-16.
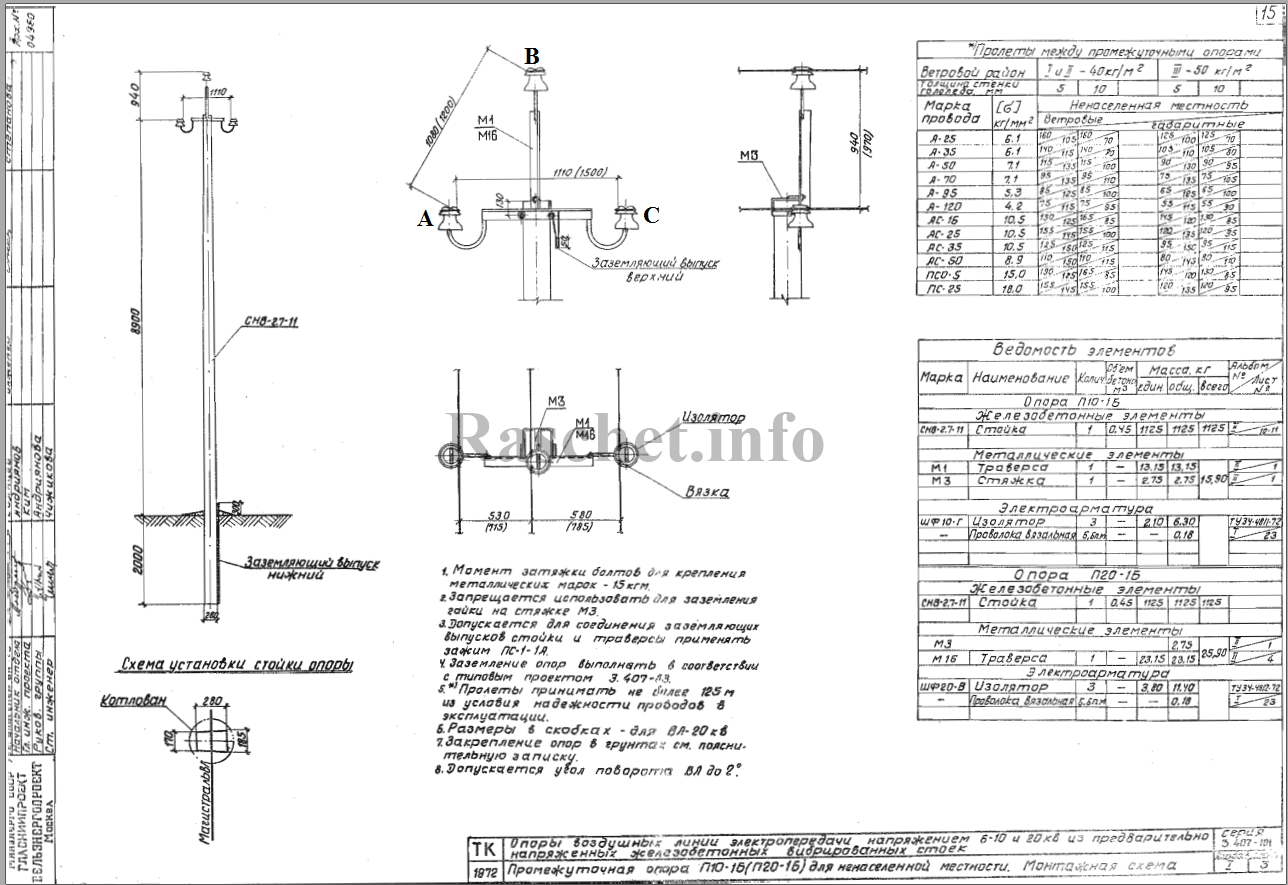
Рис.1 — Габаритный чертеж опоры П10-16
Решение
Определять индуктивное сопротивление проводов будем по формулам представленным в статье: «Определение активных и индуктивных сопротивлений проводов».
1. Определяем среднее геометрическое расстояние между проводами по формуле [Л1. с19], зная расстояния между фазами по габаритному чертежу на опору П10-16 (см. рис.1):
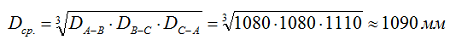
где:
- DА-В = 1080 мм — расстояние между проводами фаз А и В;
- DВ-С = 1080 мм — расстояние между проводами фаз В и С;
- DС-А = 1110 мм — расстояние между проводами фаз С и А.
2. Определяем индуктивное сопротивление для проводов марки АС-50/8,0 по формуле [Л1.с.19]:
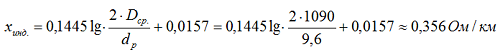
где:
- Dср. = 1090 мм – среднее геометрическое расстояние между проводами;
- dр = 9,6 мм – расчетный диаметр провода, определяется по ГОСТ 839-80, таблица 4;
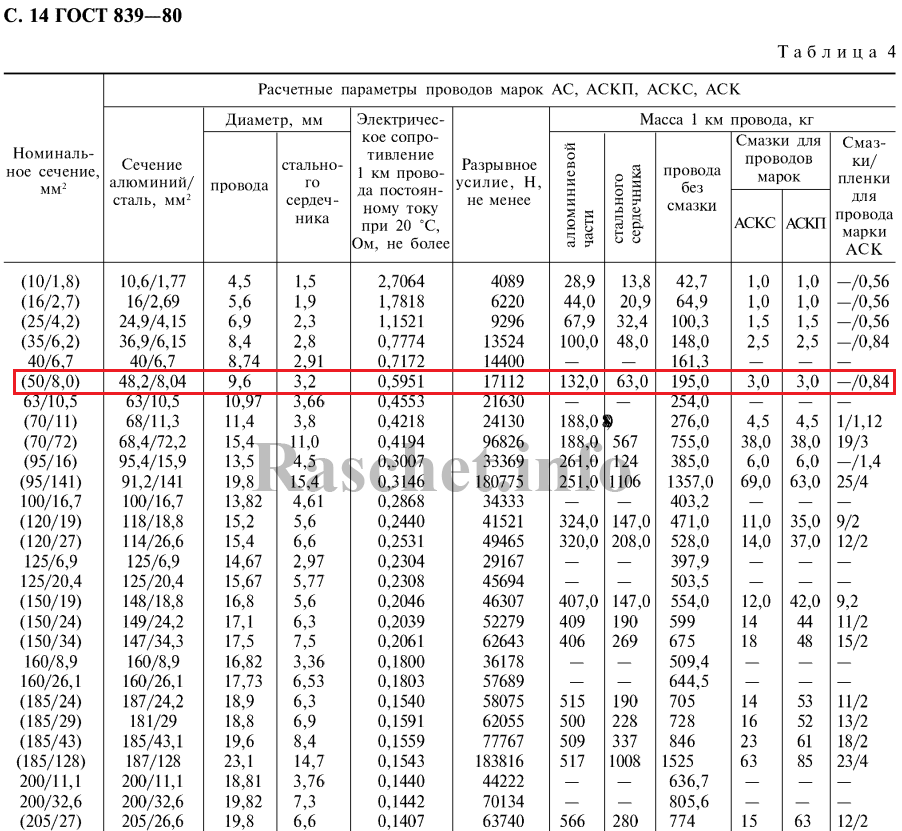
С не большой погрешностью, такой же результат можно получить по приложению П30 [Л1.с. 84], если кривую для провода сечением 50 мм2 продлить до Dср = 1,09 м, то индуктивное сопротивление будет равно 0,358 Ом/км. Принимаю хинд. = 0,356 Ом/км, так как считаю это более точное значение.
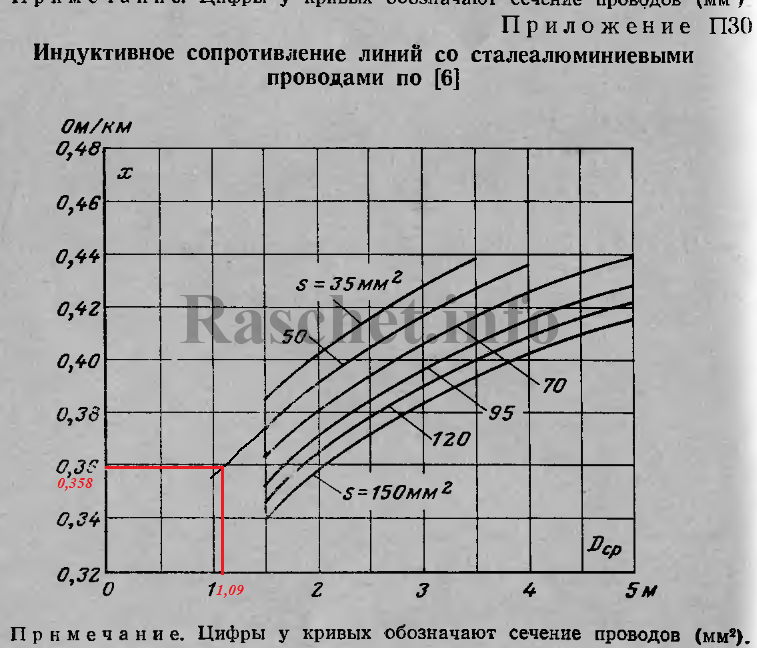
3. Определяем индуктивное сопротивление для всей линии:
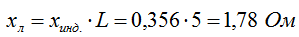
где: L = 5 км – длина воздушной линии 10 кВ.
Для упрощения расчетов индуктивного сопротивления проводов рекомендую использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.
Литература:
1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
индуктивное сопротивление, индуктивное сопротивление проводов, среднее геометрическое расстояние между проводами
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
Параметры связей
В качестве связей, то есть элементов схемы, которые соединяют два узла схемы, могут выступать линии электропередач, трансформаторы и выключатели. Рассмотрим, как определяют их параметры.
Линии электропередач
Как правило, при расчетах установившихся режимов на ПК линия электропередачи представляется П-образной схемой замещения (рисунок 1).

Линия электропередачи характеризуется продольным сопротивлением![]() и поперечной проводимостью
и поперечной проводимостью ![]()
Активная проводимость
Активная проводимость воздушных линий практически всецело определяется потерями на корону, в связи с чем, она в сильной степени зависит не только от конструкции линии, но также от рабочего напряжения и от погодных условий. В воздушных линиях (ВЛ) напряжением до 220 кВ потерями мощности на корону обычно пренебрегают, и величину принимают равной нулю. Для ВЛ напряжением 220 кВ и выше значения потерь на корону Pк для данного типа погоды, включают в нагрузки, либо можно рассчитать активные проводимости в схеме замещения:
где: Pok — удельные потери на корону, взятые из справочника для данного типа линии и для данного типа погоды, кВт/км;
l — длина линии, км;
Uном — номинальное напряжение, кВ.
Для кабельных линий активная проводимость определяет потери в изоляции кабеля. Они характеризуются тангенсом угла диэлектрических потерь, определяемым по данным завода изготовителя: ![]()
В кабельных линиях напряжением до 110 кВ этими потерями обычно пренебрегают и принимают равной нулю.
Значения , , определяются длиной линии между соседними узлами расчетной схемы и значениями удельных параметров: ![]() Величины r0, x0, b0 даются в справочной литературе, а также они могут быть рассчитаны по нижеследующим формулам, с учетом конструктивных особенностей линий электропередач.
Величины r0, x0, b0 даются в справочной литературе, а также они могут быть рассчитаны по нижеследующим формулам, с учетом конструктивных особенностей линий электропередач.
Активное сопротивление
Для алюминиевого и сталеалюминиевого проводов удельное сопротивление при температуре +20 0С может быть приближенно определено из выражения:
![]() , Ом/км,
, Ом/км,
где: F- расчетное сечение провода, мм2.
В случае, когда фаза состоит из n проводов (составляющих), полученную из вышеописанной формулы величину надо разделить на n.
При расчетах, связанных с определением потерь электроэнергии в ВЛ, необходимо учитывать зависимость активного сопротивления линии от температуры провода: ![]() где:
где:
![]() – средняя температура за базовый период, 0С;
– средняя температура за базовый период, 0С;
![]() – удельное активное сопротивление при температуре +20 0С.
– удельное активное сопротивление при температуре +20 0С.
Индуктивное сопротивление
Удельное индуктивное сопротивление провода ВЛ зависит не только от размеров самого провода, но и от расстояния между фазами, а для линий сверхвысоких напряжений, фаза которых может состоять из нескольких проводов, также и от числа составляющих в фазе, и от расстояния между ними.

где: r – радиус единичного провода, м;
![]() — среднегеометрическое расстояние между фазами, м.
— среднегеометрическое расстояние между фазами, м.
Если фаза ВЛ состоит из n проводов, то в вышеуказанное выражение вместо величины r следует подставить величину:
![]()
где: r – радиус единичного провода, м,
a – среднегеометрическое расстояние между проводами одной фазы, м.
Для кабельных линий индуктивное сопротивление меньше, чем для воздушных, так как среднегеометрическое расстояние между фазами значительно меньше. Поэтому при расчетах режимов для кабельных сетей 10 кВ и ниже можно учитывать только активное сопротивление.
Емкостная проводимость
Удельная проводимость связана с удельной емкостью ВЛ соотношением: ![]() где:
где:
![]()
– угловая частота.
В свою очередь, емкость ВЛ зависит от диаметра проводов, их взаимного расположения и расстояния между ними.
Если не учитывать влияние соседних цепей ВЛ и грозозащитных тросов (что вносит погрешность, не превышающую 5 %), то удельная емкостная проводимость ВЛ при одном проводе в фазе определяется как
При n составляющих в фазе в вышеприведенной формуле вместо r следует подставить величину rэ определенную по формуле:
Для воздушных линий напряжением ниже 110 кВ емкостную проводимость можно не учитывать.
Емкостная проводимость кабельных линий зависит от конструкции кабеля, и указывается заводом изготовителем, но для ориентировочных расчетов она может быть оценена по той же формуле. Емкостная проводимость в кабельных линиях больше, чем в воздушных, так как расстояния между проводами значительно меньше.
Лекция 2. Параметры электрических сетей
Электрическая сеть состоит из разных элементов имеющих каждый свое назначение и конструктивное выполнение. Каждый из участков электрической сети характеризуется одинаковым набором параметров (r, x, g, b, Kt ).
r – активное сопротивление, Ом;
x – реактивное сопротивление, Ом;
g – активная проводимость, См;
b – реактивная проводимость, См;
Kt – коэффициент трансформации.
Параметры отражают характерные свойства элементов сети и различаются только количественно.
Для количественного определения свойств элементов электрической сети составляется схема замещения. На ней указывают все параметры, определяющие состояние электрической сети. Схемы замещения сети составляются из схем замещения отдельных элементов, они отличаются от принципиальных схем соединения этих элементов.
Рекомендуемые материалы
Принципиальные схемы соединений (схемы коммутации) нужны только для определения направления передачи электрической энергии и степени резервирования питания потребителей. В них каждый элемент сети имеет изображение, отражающее его действие в решении задачи электроснабжения.
Схема замещения сети составляется для выполнения расчетов рабочих режимов. Каждый элемент сети в ней может отражаться несколькими подэлементами.
При характеристике симметричных рабочих режимов схемы замещения составляются на одну фазу трехфазной сети, общей является нейтраль цепи.
Потери активной мощности отражаются активными сопротивлениями (r) или проводимостями (g). Потери реактивной мощности отражаются реактивными (индуктивными) сопротивлениями или проводимостями. Генерация реактивной мощности отражается отрицательными реактивными емкостными сопротивлениями или проводимостями.
Различают продольные и поперечные ветви схем замещения. Продольными называются ветви, по которым проходит ток нагрузки. Потери мощности в этих ветвях определяются нагрузочным током.
Поперечными называются ветви, которые включены на полное напряжение (непосредственно соединены с нейтралью схемы). Потери мощности в этих ветвях определяются подведенным напряжением.
Особо отражается на схемах замещения явление трансформации. Это относится к сетям, состоящим из участков разных номинальных напряжений и рассматриваемых вместе.
Элемент трансформации отражает факт изменения параметров режима – напряжений и токов. Значения полной мощности при этом не изменяются (потери в трансформаторах отражаются другими элементами схемы).
Особыми являются и элементы, отражающие работу потребителей и пунктов питания. Они отражают факт потребления и генерации мощности, их представляют активными элементами схемы – нагрузками. При этом генерация мощности рассматривается как отрицательная нагрузка. Совокупность нагрузок определяет режим сети.
Линия электропередачи как элемент электрической сети
Передача электрической энергии по линиям обусловлена распространением электромагнитного поля в проводах и окружающим их пространстве. При действии переменного напряжения возникают переменное магнитное поле вокруг проводов и переменное электростатическое поле между фазными проводами и между каждым из проводов и землей. Условное изображение элементов этих полей показано на рисунке для одного провода ВЛ.

Возникновение переменного электрического поля приводит к появлению токов смещения (зарядных токов), величины которых зависят как от свойств диэлектрика, окружающего проводник, так и от разности потенциалов между проводом и землей, а для трехфазной линии также и между фазными проводами. Зарядные токи, накладываясь на нагрузочный ток, определяют постепенное изменение тока вдоль длины линии. Электромагнитное поле характеризуется напряженностью, также изменяющейся вдоль длины линии. Это приводит к наведению эдс самоиндукции и взаимоиндукции, неравных для различных элементов длины линии. Неравенство этих эдс определяет сложный закон изменения напряжения по линии и изменение токов смещения (зарядных токов) вдоль длины линии.
Погонные (удельные) параметры линий
Погонное (удельное) (на единицу длины) активное сопротивление rо при частоте 50 Гц и обычно применяемых сечениях алюминиевых или медных проводов и жил кабелей можно принять равным погонному омическому сопротивлению. Явление поверхностного эффекта начинает заметно сказываться только при сечениях порядка 500 мм2.
Активное сопротивление – это сопротивление при протекании по проводнику переменного тока, омическое – это сопротивление при протекании по тому же проводнику постоянного тока. Для сталеалюминиевых проводов явление поверхностного эффекта также незначительно и может не учитываться.
Значительное влияние на активное сопротивление оказывает температура материала проводников, которая зависит от температуры окружающей среды и тока нагрузки.
Погонные (удельные) реактивные (индуктивные) сопротивления фаз линий в общем случае получаются разными. Они определяются взаимным расположением фаз и геометрическими параметрами. При расчетах симметрических рабочих режимов пользуются средними значениями (независимо от транспозиции фаз линии).
Схемы замещения ЛЭП
Линия электрической сети теоретически рассматривается состоящей из бесконечно большого количества равномерно распределенных вдоль нее активных и реактивных сопротивлений и проводимостей.
Точный учет влияния распределенных сопротивлений и проводимостей сложен и необходим при расчетах очень длинных линий, которые в этом курсе не рассматривается.
На практике ограничиваются упрощенными методами расчета, рассматривая линию с сосредоточенными активными и реактивными сопротивлениями и проводимостями.
Для проведения расчетов принимают упрощенные схемы замещения линии, а именно: П-образную схему замещения, состоящую из последовательно соединенных активного (rл) и реактивного (xл) сопротивлений. Активная (gл) и реактивная (емкостная) (bл) проводимости включены в начале и конце линии по 1/2.
П-образная схема замещения характерна для воздушных ЛЭП напряжением
110-220 кВ длиной до 300-400 км.
 |
П – образная схема замещения ЛЭП напряжением 110-220 кВ длиной до 300-400 км.
Активное сопротивление определяется по формуле:  ,
,
где rо – удельное сопротивление Ом/км при tо провода + 20о,
l – длина линии, км
Активное сопротивление проводов и кабелей при частоте 50 Гц обычно примерно равно омическому сопротивлению. Не учитывается явление поверхностного эффекта.
Удельное активное сопротивление rо для сталеалюминиевых и других проводов из цветных металлов определяется по таблицам в зависимости от поперечного сечения.
Для стальных проводов нельзя пренебрегать поверхностным эффектом. Для них rо зависит от сечения и протекающего тока и находится по таблицам.
При температуре провода, отличной от 20о С сопротивление линии уточняется по соответствующим формулам.
Реактивное сопротивление определяется:  ,
,
где xо – удельное реактивное сопротивление Ом/км. Удельные индуктивные сопротивления фаз ВЛ в общем случае различны (об этом уже говорилось).
При расчетах симметричных режимов используют средние значения xо : 
 (1),
(1),
где rпр – радиус провода, см;
Дср – среднегеометрическое расстояние между фазами, см, определяется следующим выражением:
 ,
,
Где Дав, Двс, Дса – расстояния между проводами соответствующих фаз А, В, С.
Например, при расположении фаз по углам равностороннего треугольника со стороной Д, среднегеометрическое расстояние равно Д.
 |
Дав=Двс=Дас=Д
 |
При расположении проводов ЛЭП в горизонтальном положении:
Дав=Двс=Д
Дас=2Д
При размещении параллельных цепей на двухцепных опорах потокосцепление каждого фазного провода определяется токами обеих цепей. Изменение Х0 из-за влияния второй цепи зависит от расстояния между цепями. Отличие Х0 одной цепи при учете и без учета влияния второй цепи не превышает 5-6% и не учитывается в практических расчетах.
В линиях электропередач при  (иногда и при напряжении 110 и
(иногда и при напряжении 110 и
220 кВ) провод каждой фазы расщепляется на несколько проводов. Это соответствует увеличению эквивалентного радиуса. В выражении для Х0:
 (1)
(1)
вместо rпр используется
 ,
,
где rэк – эквивалентный радиус провода, см;
аср – среднегеометрическое расстояние между проводами одной фазы, см;
nф– число проводов в одной фазе.
Для линии с расщепленными проводами последнее слагаемое в формуле 1 уменьшается в nф раз, т.е. имеет вид  .
.
Удельное активное сопротивление фазы линии с расщепленными проводами определяются так : r0= r0пр / nф ,
Где r0пр – удельное сопротивление провода данного сечения, определенное по справочным таблицам. Для сталеалюминиевых проводов Х0 определяется по справочным таблицам, в зависимости от сечения, для стальных в зависимости от сечения и тока.
Активная проводимость (gл) линии соответствует двум видам потерь активной мощности:
1) от тока утечки через изоляторы;
2) потери на корону.
Токи утечки через изоляторы малы и потерями в изоляторах можно пренебречь. В воздушных линиях (ВЛ) напряжением 110 кВ и выше при определенных условиях напряженность электрического поля на поверхности провода возрастает и становится больше критической. Воздух вокруг провода интенсивно ионизируется, образуя свечение – корону. Короне соответствуют потери активной мощности. Наиболее радикальными средствами уменьшения потерь мощности на корону является увеличение диаметра провода, для линий высокого напряжения (330 кВ и выше) использование расщепления проводов. Иногда можно использовать так называемый системный способ уменьшения потерь мощности на корону. Диспетчер уменьшает напряжение в линии до определенной величины.
В связи с этим задаются наименьшие допустимые сечения по короне:
110 кВ – 70 мм2 (сейчас рекомендуется использовать сечение 95 мм2);
150 кВ – 120 мм2;
220 кВ – 240 мм2.
Коронирование проводов приводит: к снижению КПД; к усиленному окислению поверхности проводов; к появлению радиопомех.
При расчете установившихся режимов сетей до 220 кВ активная проводимость практически не учитывается.
В сетях с  при определении потерь мощности при расчете оптимальных режимов, необходимо учитывать потери на корону.
при определении потерь мощности при расчете оптимальных режимов, необходимо учитывать потери на корону.
Емкостная проводимость (вл) линии обусловлена емкостями между проводами разных фаз и емкостью провод – земля и определяется следующим образом:
 ,
,
где в0 – удельная емкостная проводимость См/км, которая может быть определена по справочным таблицам или по следующей формуле:

 (2),
(2),
где Дср – среднегеометрическое расстояние между проводами фаз; rпр – радиус провода.
Для большинства расчетов в сетях 110-220 кВ ЛЭП (линия электропередачи) представляется более простой схемой замещения:
 |
 |
Иногда в схеме замещения вместо емкостной проводимости  учитывается реактивная мощность, генерируемая емкостью линий (зарядная мощность).
учитывается реактивная мощность, генерируемая емкостью линий (зарядная мощность).
Половина емкостной мощности линии, МВАр, равна:
 (*),
(*),
где:
Uф и U – соответственно фазное и междуфазное (линейное) напряжения, кВ;
Iс – емкостный ток на землю

Из выражения для Qс (*) следует, что мощность Qс, генерируемая линий сильно зависит от напряжения. Чем выше напряжение, тем больше емкостная мощность.
Для воздушных линий напряжением 35 кВ и ниже емкостную мощность (Qс) можно не учитывать, тогда схема замещения примет следующий вид:

Для линий с  при длине > 300-400 км учитывают равномерное распределение сопротивлений и проводимостей вдоль линии.
при длине > 300-400 км учитывают равномерное распределение сопротивлений и проводимостей вдоль линии.
 |
Кабельные линии электропередачи представляют такой же П-образной
схемой замещения
как и ВЛ.
Удельные активные и реактивные сопротивления r0, х0 определяют по справочным таблицам, так же как и для ВЛ.
Из выражения для х0 и в0


видно, что х0 уменьшается, а в0 растет при сближении разных проводов.
Для кабельных линий расстояние между проводами фаз значительно меньше, чем для ВЛ и Х0 очень мало.
При расчетах режимов КЛ (кабельных линий) напряжением 10кВ и ниже можно учитывать только активное сопротивление.
 |
Емкостный ток и Qс в кабельных линиях больше чем в ВЛ. В кабельных линиях (КЛ) высокого напряжения учитывают Qс, причем удельную емкостную мощность Qc0 кВАр/км можно определить по таблицам в справочниках.
Активную проводимость (gл )учитывают для кабелей 110 кВ и выше.
Удельные параметры кабелей х0, а также Qс0 приведенные в справочных таблицах ориентировочны, более точно их можно определить по заводским характеристикам кабелей.
Характерные соотношения между параметрами линий
Активное сопротивление проводов и кабелей определяется материалом токоведущих жил и их сечениями.
С изменением сечения проводов и кабелей значительно изменяются их активные сопротивления.
Активное сопротивление обратно пропорционально сечению провода или кабеля.
Магнитное поле возникающее вокруг и внутри проводов ВЛ и жил кабелей определяет их индуктивное сопротивление. Индуктивное сопротивление зависит от взаимного расположения проводов.
Индуктивные сопротивления фазных проводов ВЛ будут одинаковыми, если они расположены по вершинам равностороннего треугольника, и будут отличаться друг от друга, если фазные провода подвешиваются в горизонтальной плоскости. Чтобы избежать нежелательной несимметрии применяют транспозицию проводов, которая заключается в том, что в нескольких точках линии фазные провода на опорах меняются местами. При этом каждый провод поочередно занимает все три возможные положения при примерно одинаковой протяженности.
Благодаря транспозиции, эдс, наводимые в фазных проводах выравниваются и индуктивные сопротивления становятся одинаковыми.
Для иллюстрации приведем пример индуктивных сопротивлений трех напряжений для средних сечений проводов и расстояний между проводами:
1) линия 6,10 кВ х0=0,362 Ом/км;
2) линия 35 кВ х0=0,401 Ом/км;
3) линия 110 кВ х0=0,433 Ом/км.
При выполнении ВЛ одиночными (нерасщепленными проводами) их индуктивное сопротивление: х0 »0,4 Ом/км.
Индуктивное сопротивление расщепленных проводов, вследствие увеличения эквивалентного радиуса, будет меньше и при расщеплении на три провода будет х0 »0,29 Ом/км.
Малая зависимость от конструктивных характеристик ВЛ также присуща и емкостной проводимости.
Среднее значение проводимости для ВЛ , выполненной одиночными проводами
во ср »2,75´10-6 См/км.
Для линий с расщепленными проводами емкостная проводимость увеличивается и при расщеплении на три провода: в0 »3,8´10-6См/км.
Для линий 110кВ при характерной для них протяженности зарядная мощность QC »10% от передаваемой;
Для линий 220кВ 30% от передаваемой;
Для линий 500кВ может быть соизмерима с передаваемой активной мощностью.
Для линий 35кВ и более низким направлением зарядную мощность можно не учитывать.
Режимы и параметры системы и сети
Состояние системы в любой момент времени или на некотором интервале времени называется режимом системы.
Режим определяется показателями, которые называются параметрами режима к их числу относятся:
1)частота,
2)активная и реактивная мощность в элементах системы,
3)напряжение в различных точках сети у потребителей,
4)величины токов,
5)величины углов расхождения векторов ЭДС и напряжения.
Различают три основных вида режимов электроэнергетических систем:
1. Нормальный установившейся режим, применительно к которому проектируется элкктрическая сеть и определяются ее технико–экономические характеристики;
2. Послеаварийный установившийся режим, наступающий после аварийного отключения какого – либо элемента сети или ряда элементов (в этом режиме система и соответственно сеть могут работать с несколько ухудшенными технико– экономическими характеристиками);
3. Переходный режим, во время которого система переходит из одного состояния к другому.
Любой режим состоит из множества различных процессов.
Различают параметры режима и параметры сети.
Параметры режима электрической сети связаны между собой определенными зависимостями, в которые входят некоторые коэффициенты, зависящие от физических свойств элементов сети, от способа соединения этих элементов между собой, а также от некоторых допущений расчетного характера.
К ним относятся полное сопротивление, активное и реактивное сопротивление, проводимости элементов, собственная и взаимная проводимости, коэффициент трансформации, коэффициент усиления.
Например, ток на участке ЛЭП определяется зависимостью: I= ; Здесь U1,U2,I – параметры режима; ZЛ – сопротивление данного участка системы (линии), является одним из параметров сети.
; Здесь U1,U2,I – параметры режима; ZЛ – сопротивление данного участка системы (линии), является одним из параметров сети.
Ряд параметров сети зависит от характера изменений ее режима, т.е. является нелинейной системой. Однако во многих практических задачах параметры сети можно полагать не изменяющимися и считать сеть линейной.
Другой вид нелинейности сети обусловлен характером соотношений между параметрами ее режима. Так, мощность, связана квадратичной зависимостью с напряжением и т.д.( S= ´U´I=
´U´I= ´U´
´U´ =
= )
)
Нелинейность такого вида надо учитывать.
Электрическую сеть рассматривают применительно к неизменному режиму системы, но в действительности такого режима не существует, и говоря об установившемся режиме имеют в виду режим малых возмущений. Отклонения параметров режима, происходит около некоторого устойчивого состояния.
Система должна быть устойчива при этих малых возмущениях. Иначе говоря, она должна обладать статической устойчивостью.
Аварийные переходные процессы возникают при резких аварийных изменениях режима, например, при к.з. элементов системы и последующем их отключении, при изменении схемы электрических соединений элементов системы.
Большие возмущения в системе при аварийных переходных процессах приводят к значительным отклонениям параметров режима к большим возмущениям, устойчивость по отношению к которым определяют как динамическую.
При этом под динамической устойчивостью понимают способность системы восстанавливать после больших возмущений свое состояние, практически близкое к исходному.
Необходимо учитывать изменения параметров режима, которые возникают при 1)увеличении передаваемых мощностей, 2)росте нагрузок и 3)изменении схемы электрических соединений в результате повреждений в сети.
Расчет режимов линий электропередач и электрических сетей
Связь между изменяющимися величинами определяется с помощью диаграмм, в которых каждая из величин характеризуется вектором. Построим диаграмму, показывающую соотношения между токами и напряжениями П-образной схемы замещения.
Расчет режима ЛЭП при заданном токе нагрузки и напряжении
в конце линии
Будем считать, что режим конца линии задан фазным напряжением Uф=сonst и отстающим током нагрузки I2. Также заданы Z12=r12+jx12, в12.
Необходимо определить 1) напряжение в начале линии – U1,2) ток в продольной части – I12, 3) потери мощности – DS12 4) ток в начале линии – I1.
 |
Расчет состоит в определении неизвестных токов и напряжений, последовательно от конца линии к началу.
Емкостный ток в конце линии 1-2, по закону Ома:
 |

Ток в продольной части линии 1-2, по первому закону Кирхгофа: I12=I2+Iкс12: (2)
Напряжение в начале линии по закону Ома: U1ф=U2ф+I12´Z12: (3)
Емкостный ток в начале линии: 
Ток в начале линии по первому закону Кирхгофа: 
Потери мощности в линии (в трех фазах): DS12=3I212´Z12: (6)
Векторная диаграмма токов и напряжений строится в соответствии с выражениями 1-5.
 |
Вначале строим известные U2ф и I2.
Полагаем что U2ф=U2ф, т.е. напряжение U2ф направлено по действительной оси. Емкостный ток  опережает на 90о напряжение U2ф. Ток I12 соединяет начало первого и конец второго суммируеммых векторов в правой части урав.(2) [I12=I2+
опережает на 90о напряжение U2ф. Ток I12 соединяет начало первого и конец второго суммируеммых векторов в правой части урав.(2) [I12=I2+ ]
]
Затем строим отдельно два слагаемых в правой части (3) [U1ф=U2ф+I12´Z12]. I12´Z12=I12´r12+I12´jx12 (7)
Вектор I12´r12 êê I12, вектор I12´jx12 опережает на 90о ток I12
Напряжение U1ф соединяет начало и конец суммируемых векторов U2ф, I12´r12, I12´jx12.
Ток  опережает U1ф на 90о.
опережает U1ф на 90о.
I1 соответствует (5) I1=I12+
В линии с нагрузкой напряжение в конце линии по модулю меньше, чем в начале U2ф<U1ф.
На линии на холостом ходу (I2=0), течет только емкостной ток, т.к. в соответствии с формулой I12=I2+Iкс12 (2) I12=Iкс12
 |
В этом случае напряжение в конце линии
повышается
U2ф>U1ф
Векторная диаграмма для такой линии:
Падение и потеря напряжения в линии
Различие в напряжениях U2ф и U1ф в П-образной схеме определяется падением напряжения на сопротивлении Z12 (Z12+jx12), вызванным током I12. Определяется это падением напряжения как сумма вектора I12r12, совпадающего по фазе с вектором I12 и вектора I12´jx12, опережающего вектор I12 на 90о.
Падение напряжения – геометрическая (векторная) разность между комплексами напряжений начала и конца линий.
 |
На рис. падение напряжения это вектор  , т.е.
, т.е. 
разность комплексных значений по концам линий, используется для характеристики режима линии.
Продольной составляющей падения напряжения DUк12 называют проекцию падения напряжения на действительную ось или на напряжение U2, DUк12=АС. Индекс “к” означает , что Uк12 – проекция на напряжение конца линии U2.
Обычно DUк12 выражается через данные в конце линии: U2, Pк12, Qк12.
Поперечная составляющая падения напряжения dUк12 – это проекция падения напряжения на мнимую ось, jdUк12=СВ. Т. о. U1-U2= ´I12´Z12=DUк12+jdUк12.
´I12´Z12=DUк12+jdUк12.
Величина dUк12 определяет сдвиг вектора напряжения в начале линии (U1) на угол d по отношению к вектору напряжения в ее конце (U2).
Часто используют понятие потеря напряжения – это алгебраическая разность между модулями напряжений начала (U1) и конца (U2) линий.
На рис. çU1ê– êU2ê=АД.
Если поперечная составляющая dUк12 мала (например, в сетях Uном £ 110кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения напряжения.
Потеря напряжения является показателем изменения относительных условий работы потребителей в начале и в конце линии.
Расчет режимов линий электропередач и электрических сетей
при заданной мощности нагрузки
При подаче энергии по линии от начала к ее концу имеют место потери реактивной мощности. Они обусловлены реактивным сопротивлением линии и соответствующим ему реактивным сопротивлением схемы замещения этой линии. При передаче энергии имеют место и потери активной мощности, расходуемой на нагревание проводов. Поэтому в схеме замещения следует различать полную мощность до сопротивления Z12(r12+jx12), Sн12 и после него Sк12.
Расчет режима ЛЭП при заданной мощности нагрузки и напряжении
в конце линии
Задано напряжение в конце линии U2=сonst. Известна мощность нагрузки S2, напряжение U2, сопротивление и проводимость линии Z12=r12+jx12, в12.
 |
Необходимо определить напряжение U1, мощности в конце и в начале продольной части линии Sк12, Sн12, потери мощности DS12, мощность в начале линии S1. Для проверки ограничений по нагреву иногда определяют ток в линии I12.
Расчет аналогичен расчету при заданном токе нагрузке (I2), и состоит в последовательном определении от конца линии к началу неизвестных мощностей и напряжений при использовании I закона Кирхгофа и закона Ома. Будем использовать мощности трех фаз и линейные напряжения.
Зарядная (емкостная) мощность трех фаз в конце линии:
–jQкс12=3I*кс12´U2ф=
Мощность в конце продольной части линии по I закону Кирхгофа: Sк12=S2 – jQкс12
Потери мощности в линии: DS12=3I212Z12=
Ток в начале и в конце продольной ветви линии одинаков.
Мощность в начале продольной ветви линии больше, чем мощность в конце, на величину потерь мощности в линии, т.е. Sн12=Sк12+DS12
Линейное напряжение в начале линии по закону Ома равно:
U1=U2+ I12Z12=U2+
I12Z12=U2+
Емкостная мощность в начале линии: –jQнc12=
Мощность в начале линии: S1=Sн12 – jQнс12
Под влиянием зарядной мощности Qс реактивная мощность нагрузки Q2 в конце, схема замещения уменьшается. Аналогичное явление имеет место и в начале схемы замещения, где реактивная мощность Qс уменьшает реактивную мощность в начале линии.
Это свидетельствует о том, что зарядная мощность сокращает реактивную мощность, поступающую от станции в линию для питания нагрузки. Поэтому зарядная мощность условно может рассматриваться как “генератор” реактивной мощности.
В линии электрической сети имеют место как потери, так и генерация реактивной мощности.
От соотношения потерь и генерации реактивной мощности зависит различие между реактивными мощностями в начале и конце линии.
Расчет режима ЛЭП при заданной мощности нагрузки и напряжении
в начале линии
Задано напряжение в начале линии.
Схема замещения:
 |
U1=сonst. Известны S2, U1 ,Z12=r12+jx12, в12.
Необходимо определить U2, Sк12, Sн12, DS12, S1
Т.к. U2 неизвестно, то невозможно определить последовательно от конца линии к началу определить неизвестные токи и напряжения по I закону Кирхгофа и закону Ома.
1-й способ.
Нелинейное уравнение узловых напряжений для узла 2 имеет вид:
Y22U2+Y12U1=I2(U)=S*2/U*2
Это уравнение можно решить и найти неизвестное напряжение U2, а затем найти все мощности по выражениям:

Но можно осуществить приближенный расчет в два этапа.
2-й способ.
1 этап:
Предположим, что U2=Uном (7) и определим потоки и потери мощности аналогично выражениям (1)-(4), используя (7) получим:

Если Вам понравилась эта лекция, то понравится и эта – 2 Электродвижущие силы обмоток переменного тока.
2 этап:
Определим напряжение U2 по закону Ома, используя поток мощности Sн12, найденный на 1 этапе. Для этого используем закон Ома в виде:  (7),
(7),
но выразим ток I12 через Sн12 и U1: 
Потоки мощности на 1 этапе определены приближенно, поскольку в формулах вместо U2 использовали Uном.
Соответственно напряжение U2 на 2 этапе также определено приближенно, т.к. в последней формуле для U2 используется приближенное значение Sн12, определенное на 1 этапе.
Возможно итерационное повторение расчета, т.е. повторение 1-го и 2-го этапов для получения более точных значений мощности и напряжений. При проведении расчетов вручную, а не на ЭВМ, такое уточнение не требуется.


