Основные выводы:
-
Формула для расчета среднего процента – [(процент 1 + процент 2) (объем выборки 1 + объем выборки 2)] x 100
-
Используйте средний процент при определении среднего значения двух или более процентов от целого.
Расчет среднего процента от чего-либо может показаться простой задачей, но эта концепция может быть сложнее, чем может показаться на первый взгляд. Хотя в некоторых случаях вы можете просто усреднить два процента, сложив их и разделив на количество используемых процентов, в других случаях вам может потребоваться учесть такие факторы, как размер выборки.
В этой статье мы обсудим проценты и способы вычисления среднего процента, а также приведем примеры использования формулы среднего процента в различных сценариях.
Понимание процентных соотношений
В базовом смысле проценты – это соотношение или доля чего-либо от 100. Например, если у вас есть коробка со 100 шоколадными конфетами и 35 из них наполнены ванильным кремом, это означает, что 35% шоколадных конфет имеют вкус ванильного крема. Проценты используются в различных аспектах повседневной жизни, в том числе в школе и на предприятиях. Расчет среднего процентного показателя также может быть использован в ряде различных сценариев. Например, инвестор может захотеть определить, как два разных запаса изменяются со временем по отношению друг к другу. Чтобы понять эту взаимосвязь, инвестору необходимо знать, как рассчитать среднее значение двух процентов запасов.
Как рассчитать среднее значение
Прежде чем мы сможем объяснить, как рассчитать средний процент, мы должны сначала определить, как рассчитать среднее значение. Среднее значение набора чисел – это просто сумма чисел, деленная на общее количество значений в наборе. Например, чтобы найти среднее значение 12, 15, 24, 78, 3, 313 и 10, просто сложите эти числа (12 + 15 + 24 + 78 + 3 + 313 + 10 = 455) и разделите на общее количество значений в наборе (7), чтобы получить среднее значение 65.
Как рассчитать средний процент
Вычисление среднего значения двух или более процентов требует иного набора шагов, чем определение среднего значения двух или более обычных чисел. При вычислении среднего процента необходимо учитывать несколько моментов, включая тот факт, что часто сначала необходимо вычислить реальные числа, которые представляет процент.
Для расчета среднего процента в большинстве случаев используйте следующие шаги:
1. Преобразуйте проценты, которые вы хотите усреднить, в десятичные числа
Первый шаг в вычислении среднего процентного показателя – перевести проценты в десятичные числа. Допустим, вы хотите определить среднее значение 30% от 150 и 25% от 200. Преобразуйте эти два процента в десятичные числа, разделив их оба на 100. Это означает, что 30% – это 0.3 как десятичная дробь и 25% – это .25 как десятичная дробь.
2. Определите число, которое представляет каждая десятичная дробь
После того, как вы перевели проценты в десятичные дроби, вам нужно найти число, которое представляет каждая десятичная дробь. Для этого нужно умножить десятичную дробь на общее количество в выборке. Таким образом, используя предыдущий пример, вы умножите 0.3 на 150, чтобы получить 45 и умножить .25 на 200, чтобы получить 50.
3. Сложите числа вместе
Следующим шагом будет сложение двух чисел, найденных на предыдущем этапе. Таким образом, 45 плюс 50 равно 95.
4. Сложите объемы выборки
Также необходимо сложить объемы выборки для каждого процента. Таким образом, 150 плюс 200 равно 350.
5. Рассчитайте среднее процентное значение
Чтобы найти средний процент из двух процентов в этом примере, нужно сначала разделить сумму двух процентных чисел на сумму двух объемов выборки. Итак, 95 разделить на 350 равно 0.27. Затем вы умножаете десятичную дробь на 100, чтобы получить средний процент. Итак, 0.27 умножить на 100 равно 27 или 27%. Это означает, что средний процент 30% от 150 и 25% от 200 составляет 27%.
Формула среднего процента
Ниже приведена формула, которая может быть использована для расчета большинства средних процентных показателей:
[(Процент 1 + процент 2)(объем выборки 1 + объем выборки 2)] x 100 = средний процент
В этой формуле процент 1 представляет собой десятичное значение данного процента от объема выборки 1. Чтобы определить значение процента 1, вы должны сначала преобразовать процент в десятичную дробь, а затем умножить десятичную дробь на размер выборки. Повторите этот шаг, чтобы определить десятичное значение процента 2 в этой формуле. После того как вы рассчитали десятичные значения каждого процента для каждого данного размера выборки, вы складываете эти десятичные значения вместе и делите полученное число на общую сумму обоих размеров выборки. Затем нужно умножить это значение на 100, чтобы получить средний процент.
Пример расчета средних процентов
Ниже приведен пример расчета среднего процента в реальных условиях:
Компания XYZ хочет определить средний процент того, сколько продуктов было продано из двух различных категорий продуктов в данном году. В первой категории товаров компания произвела 500 товаров и продала 75% из них. Во второй категории компания произвела 400 продуктов и продала 60% из них.
Для определения среднего процента проданных товаров из обеих категорий выполняются следующие действия:
-
Переведите оба процента в десятичные дроби. Итак, 75 разделить на 100 равно .75 и 60 разделить на 100 равно .60. Это дает вам .75 и .60 как представление двух процентов проданных продуктов из обеих категорий товаров.
-
Умножьте десятичные значения на общее количество продукции, произведенной в каждой категории. Итак,, .75 умножить на 500 равно 375 и .60 умножить на 400 равно 240. Это означает, что 75% от 500 составляет 375, а 60% от 400 равно 240.
-
Сложите два числа, которые представляют процентное соотношение товаров из каждой категории. Итак, 375 плюс 240 равно 615.
-
Сложите вместе общее количество продукции, произведенной в каждой категории. Так, 500 плюс 400 равно 900.
-
Разделите сумму процентов на сумму общего количества продуктов, произведенных в каждой категории. Так, 615, разделенное на 900, равно 0.68.
-
Умножьте десятичную дробь на 100, чтобы получить средний процент. Таким образом, 0.68 умножить на 100 равно 68, или 68%.
Используя эту формулу, компания XYZ продала в среднем 68% продуктов из двух категорий товаров, которые были проанализированы.
Как посчитать средний процент
Проценты показывают величину какой-либо произвольно выбранной доли по отношению к целому. Показатели, выраженные в процентах, называются относительными и не имеют размерности. При измерении изменения какого-либо показателя за несколько последовательных периодов времени бывает необходимо вычислить среднее значение процентного изменения за каждый из этих периодов.
Инструкция
Если даны начальное и конечное абсолютные значения показателя, средний процент изменения которого надо рассчитать, то сначала определите общий процент роста или падения. Полученную величину поделите на количество периодов, для каждого из которых нужно определить среднее значение. Например, если количество занятых на производстве работников на начало прошлого года было равно 351, а на начало текущего года вросло до 402, то за 100% надо принять число 351. Исходный показатель за весь период увеличился на 402-351=51, что составляет 51/351*100≈14,53%. Для определения среднего процента роста по месяцам минувшего года разделите это число на 12: 14,53/12≈1,21%.
Если в исходных данных приведены начальное значение показателя и абсолютные величины его изменения по периодам, то начните с суммирования изменений по периодам. Затем, как и в предыдущем шаге, определите величину полученного числа в процентах от исходного значения и поделите результат на количество суммированных значений. Например, если на начало года число служащих было равно 402, затем в Январе было принято дополнительно 15 человек, а в Феврале и Марте было сокращено по 3 работника, то общее изменение численности за квартал составило 15-3-3=9 или 9/402*100≈2,24%. Средний процент изменения за каждый месяц первого квартала будет равен 2,24/3≈0,75%.
Если величины изменения по периодам даны в процентах от абсолютного значения на начало каждого периода, то такой процент называют «сложным». В этом случае тоже начните с вычисления изменения показателя за все периоды, а затем поделите полученное число на количество периодов. При этом не забывайте об изменении веса каждого процента на начало очередного периода. Например, пусть из условий задачи известно, что за первый квартал численность работников выросла на 10%, за второй – на 15%, за третий – на 5%, за четвертый – на 8%. Тогда после первого квартала численность стала равна 100+10=110%, после второго 110+(110/100*15)=126,5%, после третьего 126,5+(126,5/100*5)=132,825%, после четвертого 132,825+(132,825/100*8)=143,451%. Из этого вытекает, что в среднем по кварталам рост составлял 43,451/4≈10,86%.
Источники:
- как рассчитать изменение в процентах
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Сложный процент, среднегодовая доходность, дисконтирование и приращение
В этой статье рассмотрим базовые понятия, которые пригодятся любому инвестору: сложный процент, среднегодовая доходность, дисконтирование и приращение. Google-таблица с формулами, используемыми в тексте, находится по ссылке.
Сложный процент – Восьмое Чудо Света
Сложные проценты — самая мощная сила в природе! Сложный процент – это Восьмое чудо света. Тот, кто понимает это – зарабатывает его, тот, кто не понимает – платит его.Альберт Эйнштейн

Альберт Эйнштейн знал силу сложных процентов
Сложный процент – эффект, когда процент в конце одного периода прибавляется к основной сумме и в следующий период процент уже начисляется на новую сумму. И такое действие может происходить на всем периоде инвестирования (прибыль реинвестируется).
Формула, если капитализация раз в год:
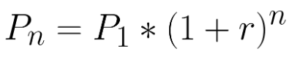
Пример: на три года инвестируем 100 000 рублей под ставку в 10% годовых. Капитализация раз в год. Проценты реинвестируются.
![]()
Формула, если капитализация несколько раз в год:
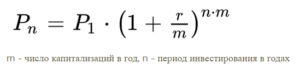
Пример: на три года инвестируем 100 000 рублей под ставку в 10% годовых, капитализация один раз в месяц. Проценты реинвестируются ежемесячно.
![]()
Сложный процент порождает иллюзию, что через 10-15-20-25-30 лет можно легко стать рантье и жить на проценты. Например, фондовый рынок дает 20% в год, у нас есть 30 лет и мы инвестируем 1 000 000 рублей. “Инвесторская сказка” может обещать следующее:
![]()
Инвестор “виртуально в будущем” с одного миллиона заработал 237 376 313 рублей.
Для среднестатистического человека это колоссальная сумма.
Что здесь не так?
Реальный сложный процент
Не так здесь то, что инфляция за это время составит тоже огромную величину. Для правильного восприятия роста благосостояния лучше считать эффекты сложного процента по реальной ставке (т.е. с учетом инфляции).
Например, если среднегодовая прогнозируемая инфляция составит 10%, то среднегодовая ожидаемая реальная доходность составит:
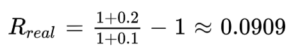
В итоге реальное благосостояние инвестора составит весомую, но не астрономическую сумму:
![]()
Инвестор становится богаче не в 237 раз, а в 13 раз! Это тоже отличный результат. К такому результату надо стремиться. В реальности очень трудно получать реальную доходность в 9% на протяжении длительного периода времени. В среднем можно получать реальную доходность от 3% до 9%.
Это не означает, что не нужно инвестировать. Это означает, что нужно смотреть правде в глаза.
Среднегодовая доходность
Для сравнения разных способов инвестиций на дистанции нам необходимо уметь считать среднегодовую доходность наших инвестиций. Формула при условии, что мы один раз инвестировали деньги и потом получили некий результат:
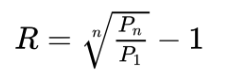
Пример: в 2014 году мы инвестировали на биржу 100 000 рублей. Через 3 года у нас на счету стало 285 000 рублей. Рассчитаем среднегодовую доходность за три года:
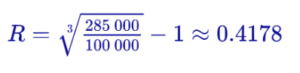
Самопроверка:
![]()
Экономический смысл: если бы выбирали между банком и биржей по доходности, то нам нужно было бы найти банк, который предлагает ставку в размере 41,78% или выше на протяжении 3 лет ежегодно.
Формула для расчета среднегодовой доходности, если нам известны результаты инвестиций по годам:
![]()
Пример: в первый год инвестор заработал 15%, во второй потерял -10% и в третий заработал 29%. Какова его среднегодовая доходность?
![]()
Несмотря на два очень удачных года среднегодовая доходность инвестора оказалась на уровне всего лишь 10,11%.
Периоды падения очень отрицательно сказываются на среднегодовой доходности!
Давайте ещё раз сделаем самопроверку и окончательно поймем экономический смысл. Посчитаем сначала с учетом ежегодной доходности по каждому году результат инвестирования:

Разница в 15 рублей получилась за счет округления 10,11%.
Плавная доходность лучше всплесков
Многие инвесторы (особенно новички) гонятся за огромными доходностями, получают их в один год и терпят “незначительные” убытки в следующий год. Давайте рассмотрим ещё один показательный случай из практики, что “медленные инвесторы” в итоге выигрывают:
Инвестор 1 получил доходность в первый год +90%, во второй год убыток в размере -21% и в третий год доходность в размере +15%.
Инвестор 2 получил доходность в первый год +21%, во второй год +32% и в третий год всего лишь +9%.
Кто заработал больше?
1.9*0.79*1.15 = 1.72615
Среднегодовая доходность первого 19,96%.
1.21*1.32*1.09 = 1.784112
Среднегодовая доходность второго 21,29%.
“Сверхдоходность” в 90% не спасла “быстрого” инвестора. Его итоговый результат оказался ниже, чем результат работы “плавного” инвестора.
Минусы вредны для портфеля. Если портфель упал на 20%, то ему надо заработать 25%, чтобы хотя бы восстановиться.
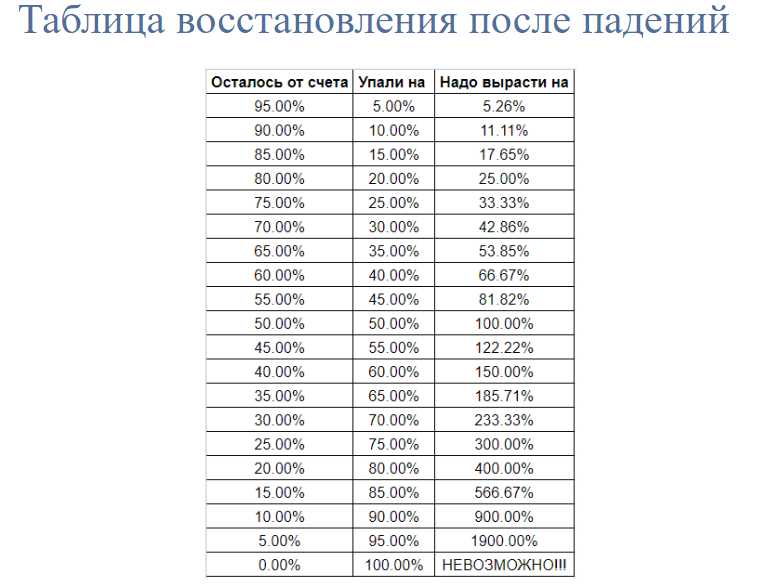
Сколько нужно зарабатывать после падений для восстановления первоначальной суммы на счете
Дисконтирование
Дисконтирование – это процесс определения текущей стоимости денег, когда известна их будущая стоимость. Дисконтирование дохода применяется для оценки будущих денежных поступлений (прибыль, проценты, дивиденды) с позиции текущего момента.
Дисконтирование выполняется путём умножения будущих денежных потоков (потоков платежей) на коэффициент дисконтирования:
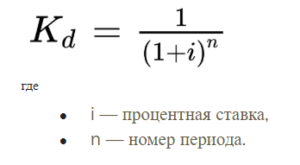
Экономический смысл дисконтирования (на примере)
Через 2 года Вам нужно будет 1 000 000 рублей, чтобы купить автомобиль. У Вас есть возможность положить деньги в банк под ставку 10%. Какой суммой денег нужно обладать сейчас, чтобы в будущем купить автомобиль?
![]()
Нам нужно будет 826 446,29 рублей, чтобы сейчас их инвестировать с доходность в 10% ежегодно и через 2 года снять 1 000 000 рублей.
Проверим это:
826 446.29 * 1.1*1.1 = 1 000 000 рублей.
Наращение
Наращение – это процесс приведения текущей стоимости денег к будущей. Наращение позволяет получить оценку той суммы, на которую можно рассчитывать в будущем, инвестировав некоторым образом исходную сумму. Это процесс, обратный дисконтированию.
Базовая формула наращения, если ставка доходности одинакова для каждого периода:
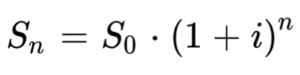
Экономический смысл наращения
Сейчас у нас есть 1 000 000 рублей. Мы хотим на 3 года его инвестировать на биржу, ожидаемая доходность инвестиций 15%. Какая сумма будет на счете через 3 года?
![]()
Наращение делают по сложному проценту. Возможно делать наращение по разным ставкам (в каждый период своя доходность).
По сути наращение и есть работа сложных процентов на будущие периоды.
Понимание силы сложных процентов позволяет более рассудительно и долгосрочно относиться к инвестициям.
Видеоверсия материала
Рады подарить вам постоянную скидку 20% для биржи Binance:
(зарегистрируйтесь сейчас, воспользоваться можно будет позже)
Автор в Telegram:
9889 Всего просмотров 1 Сегодня просмотров
Рассмотрим несколько более сложную задачу.
Фабрика выпустила:

Найти средний процент выпуска I сорта за год.
Определяя количество тонн изделий I сорта по каждому кварталу, предварительно находим, что всего за год выпущено  том числе I сорта:
том числе I сорта:

что составляет 78,7% всего выпуска.
Если взять просто среднее число процентов выпуска I сорта по кварталам, то получим ( что заметно больше правильного ответа.
что заметно больше правильного ответа.
Чем объяснить это расхождение?
Для расчета среднего процента из нескольких процентных ставок нужно использовать взвешенное среднее арифметическое значение. Формула для расчета такого среднего значения будет выглядеть следующим образом:
средний процент = (сумма процентных ставок * доли каждой ставки) / сумма долей
где:
– сумма процентных ставок – сумма всех процентных ставок, которые нужно усреднить;
– доли каждой ставки – доля каждой процентной ставки от общей суммы процентных ставок;
– сумма долей – общая сумма долей всех процентных ставок.
Например, у вас есть инвестиции, где вы получили доходность 4% на 1000 долларов и 6% на 5000 долларов. Чтобы найти средний процент, используем формулу:
средний процент = (0,04 * 1000 + 0,06 * 5000) / (1000 + 5000) = 0,057 или 5,7%
Таким образом, средний процент для ваших инвестиций равен 5,7%.
Калькулятор среднего процента из нескольких процентов
Этот калькулятор позволяет пользователю ввести три пары значений: сумму и процентную ставку для каждой из трех инвестиций. После того, как пользователь нажимает кнопку “Рассчитать средний процент”, калькулятор вычисляет средневзвешенную процентную ставку на основе введенных значений.
Количество пар значений:
