Средний годовой темп роста и средний годовой темп прироста
Прежде
всего
отметим,
что
приведенные
в
таблице
темпы
роста
( гр.7
и
8) являются
рядами
динамики
относительных
величин
— производными
от
интервального
ряда
динамики
(гр.2).
Ежегодные
темпы
роста
(гр.7)
изменяются
по
годам
( 105%; 103,8%; 105,5%; 101,7%). Как
вычислить
среднюю
величину
из
ежегодных
темпов
роста
? Эта
величина
называется
среднегодовым
темпом
роста.
Среднегодовой
темп
роста
исчисляется
в
следующей
последовательности:
-
сначала
по
формуле
средней
геометрической
исчисляют
среднегодовой
коэффициент
роста
(снижения)
— -
на
базе
среднегодового
коэффициента
определяют
среднегодовой
темп
роста
()путем
умножения
коэффиицента
на
100%:
Среднегодовой
темп
прироста
( определяется
путем
вычитания
из
темпа
роста
100%.
Среднегодовой
коэффициент
роста
( снижения
) по
формулам
средней
геометрической
может
быть
исчислен
двумя
способами:
1)
на
базе
абсолютных
показателей
ряда
динамики
по
формуле:
-
n —
число
уровней; -
n
— 1 —
число
лет
в
период;
2)
на
базе
ежегодных
коэффициентов
роста
по
формуле
-
m —
число
коэффициентов.
Результаты
расчета
по
формулам
равны,
так
как
в
обеих
формулах
показатель
степени
— число
лет
в
периоде,
в
течение
которого
происходило
изменение.
А
подкоренное
выражение
— это
коэффициент
роста
показателя
за
весь
период
времени
(см.
табл.
11.5, гр.6,
по
строке
за
1998 г.).
Среднегодовой
темп
роста
равен
Среднегодовой
темп
прироста
определяется
путем
вычитания
из
среднегодового
темпа
роста
100%. В
нашем
примере
среднегодовой
темп
прироста
равен
Следовательно,
за
период
1995 — 1998 гг.
объем
производства
продукта
“А”
в
среднем
за
год
возрастал
на
4,0%. Ежегодные
темпы
прироста
колебались
от
1,7% в
1998 г.
до
5,5% в
1997 г.
(за
каждый
год
темпы
прироста
см.
в
табл.
11.5, гр.
9).
Среднегодовой
темп
роста
(прироста)
позволяет
сравнивать
динамику
развития
взаимосвязанных
явлений
за
длительный
период
времени
(например,
среднегодовые
темпы
роста
численности
работающих
по
отраслям
экономики,
объема
производства
продукции
и
др.),
сравнивать
динамику
какого-либо
явления
по
разным
странам,
исследовать
динамику
какого-либо
явления
по
периодам
исторического
развития
страны.
7.
Индексами называют
сравнительные
относительные
величины,
которые
характеризуют
изменение
сложных
социально-экономических
показателей
(показатели,
состоящие
из
несуммируемых
элементов)
во
времени,
в
пространстве,
по
сравнению
с
планом.
Индекс
– это
результат
сравнения
двух
одноименных
показателей,
при
исчислении
которого
следует
различать
числитель
индексного
отношения
(сравниваемый
или
отчетный
уровень)
и
знаменатель
индексного
отношения
(базисный
уровень,
с
которым
производится
сравнение).
Выбор
базы
зависит
от
цели
исследования.
Если
изучается
динамика,
то
за
базисную
величину
может
быть
взят
размер
показателя
в
периоде,
предшествующем
отчетному.
Если
необходимо
осуществить
территориальное
сравнение,
то
за
базу
можно
принять
данные
другой
территории.
За
базу
сравнения
могут
приниматься
плановые
показатели,
если
необходимо
использовать
индексы
как
показатели
выполнения
плана.
Индексы
формируют
важнейшие
экономические
показатели
национальной
экономики
и
ее
отдельных
отраслей.
Индексные
показатели
позволяют
осуществить
анализ
результатов
деятельности
предприятий
и
организаций,
выпускающих
самую
разнообразную
продукцию
или
занимающихся
различными
видами
деятельности.
С
помощью
индексов
можно
проследить
роль
отдельных
факторов
при
формировании
важнейших
экономических
показателей,
выявить
основные
резервы
производства.
Индексы
широко
используются
в
сопоставлении
международных
экономических
показателей
при
определении
уровня
жизни,
деловой
активности,
ценовой
политики
и
т.д.
Существует
два
подхода
в
интерпретации
возможностей
индексных
показателей:
обобщающий
(синтетический)
и
аналитический,
которые
в
свою
очередь
определяются
разными
задачами.
Суть
обобщающего
подхода
– в
трактовке
индекса
как
показателя
среднего
изменения
уровня
исследуемого
явления.
В
этом
случае
основной
задачей,
решаемой
с
помощью
индексных
показателей,
будет
характеристика
общего
изменения
многофакторного
экономического
показателя.
Аналитический
подход
рассматривает
индекс
как
показатель
изменения
уровня
результативной
величины,
на
которую
оказывает
влияние
величина,
изучаемая
с
помощью
индекса.
Отсюда
и
иная
задача,
которая
решается
с
помощью
индексных
показателей:
выделить
влияние
одного
из
факторов
в
изменении
многофакторного
показателя.
От
содержания
изучаемых
показателей,
методологии
расчета
первичных
показателей,
целей
и
задач
исследования
зависят
и
способы
построения
индексов.
По
степени
охвата
элементов
явления
индексы
делят
на
индивидуальные
и
общие
(сводные).
Индивидуальные
индексы (i)
– это
индексы,
которые
характеризуют
изменение
только
одного
элемента
совокупности.
Общий
(сводный)
индекс (I)
характеризует
изменение
по
всей
совокупности
элементов
сложного
явления.
Если
индексы
охватывают
только
часть
явления,
то
их
называют
групповыми.
В
зависимости
от
способа
изучения
общие
индексы
могут
быть
построены
или
как
агрегатные
(от
лат.
аggrega
– присоединяю)
индексы,
или
как
средние
взвешенные
индексы
(средние
из
индивидуальных).
Способ
построения агрегатных
индексов заключается
в
том,
что
при
помощи
так
называемых
соизмерителей
можно
выразить
итоговые
величины
сложной
совокупности
в
отчетном
и
базисном
периодах,
а
затем
первую
сопоставить
со
второй.
В
статистике
имеют
большое
значение
индексы
переменного
и
фиксированного
состава,
которые
используются
при
анализе
динамики
средних
показателей.
Индексом
переменного
состава называют
отношение
двух
средних
уровней.
Индекс
фиксированного
состава есть
средний
из
индивидуальных
индексов.
Он
рассчитывается
как
отношение
двух
стандартизованных
средних,
где
влияние
изменения
структурного
фактора
устранено,
поэтому
данный
индекс
называют
еще
индексом
постоянного
состава.
В
зависимости
от
характера
и
содержания
индексируемых
величин
различают индексы
количественных (объемных) показателей и индексы
качественных
показателей.
10.2.
Индексы
количественных
показателей
К индексам
количественных
(объемных)
показателей относятся
такие
индексы,
как
индексы
физического
объема
производства
продукции,
затрат
на
выпуск
продукции,
стоимости
продукции,
а
также
индексы
показателей,
размеры
которых
определяются
абсолютными
величинами.
Используются
различные
виды
индексов
количественных
показателей.
Индекс
физического
объема
продукции (ФОП)
отражает
изменение
выпуска
продукции.
Индивидуальный
индекс
ФОП
отражает
изменение
выпуска
продукции
одного
вида
и
определяется
по
формуле
(10.1)
где
q1 и
q0 –
количество
продукции
данного
вида
в
натуральном
выражении
в
текущем
и
базисном
периодах.
Агрегатный
индекс ФОП
(предложен Э.
Ласпейресом)
отражает
изменение
выпуска
всей
совокупности
продукции,
где
индексируемой
величиной
является
количество
продукции
q, а
соизмерителем
– цена
р:

где
q1 и
q0 –
количество
выработанных
единиц
отдельных
видов
продукции
соответственно
в
отчетном
и
базисном
периодах;
p0 –
цена
единицы
продукции
(отдельного
вида)
в
базисном
периоде.
При
вычислении
индекса
ФОП
в
качестве
соизмерителей
может
выступать
также
себестоимость
продукции
или
трудоемкость.
Средние
взвешенные
индексы
ФОП
используются
в
том
случае,
если
известны
индивидуальные
индексы
объема
по
отдельным
видам
продукции
и
стоимость
отдельных
видов
продукции
(или
затраты)
в
базисном
или
отчетном
периоде.
Средний
взвешенный
арифметический
индекс ФОП
определяется
по
формуле

где
iq –
индивидуальный
индекс
по
каждому
виду
продукции;
q0 p0 –
стоимость
продукции
каждого
вида
в
базисном
периоде.
Средний
взвешенный
гармонический
индекс ФОП
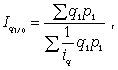
где
q1 p1 –
стоимость
продукции
каждого
вида
в
текущем
периоде.
Аналогично
рассчитывается индекс
затрат
на
выпуск
продукции (ЗВП),
который
отражает
изменение
затрат
на
производство
и
может
быть
как
индивидуальным,
так
и
агрегатным.
Индивидуальный
индекс ЗВП
отражает
изменение
затрат
на
производство
одного
вида
и
определяется
по
формуле

где
z1 и
z0 –
себестоимость
единицы
продукции
искомого
вида
в
текущем
и
базисном
периодах;
q1 z1 и
q0 z0 –
суммы
затрат
на
выпуск
продукции
искомого
вида
в
текущем
и
базисном
периодах.
Агрегатный
индекс ЗВП
характеризует
изменение
общей
суммы
затрат
на
выпуск
продукции
за
счет
изменения
количества
выработанной
продукции
и
ее
себестоимости
и
определяется
по
формуле
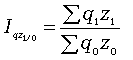
где
q1 z1 и
q0 z0 –
затраты
на
выпуск
продукции
каждого
вида
соответственно
в
отчетном
и
базисном
периодах.
Рассмотрим
построение индекса
стоимости
продукции
(СП),
который
может
определяться
и
как
индивидуальный,
и
как
агрегатный.
Индивидуальный
индекс СП
характеризует
изменение
стоимости
продукции
данного
вида
и
имеет
вид:

где
p1 и
p0 –
цена
единицы
продукции
данного
вида
в
текущем
и
базисном
периодах;
q1 p1 и
q0 p0 –
стоимость
продукции
данного
вида
в
текущем
и
базисном
периодах.
Агрегатный
индекс СП
(товарооборота)
характеризует
изменение
общей
стоимости
продукции
за
счет
изменения
количества
продукции
и
цен
и
определяется
по
формуле

10.3.
Индексы
качественных
показателей.
Факторный
анализ
Качественные
показатели
определяют
уровень
исследуемого
итогового
показателя
и
определяются
путем
соотношения
итогового
показателя
и
определенного
количественного
показателя
(например,
средняя
заработная
плата
определяется
путем
соотношения
фонда
заработной
платы
и
количества
работников).
К
индексам
качественных
показателей
относятся
индексы
цен,
себестоимости,
средней
заработной
платы,
производительности
труда.
Самым
распространенным
индексом
в
этой
группе
является
индекс
цен.
Индивидуальный
индекс
цен характеризует
изменение
цен
по
одному
виду
продукции
и
определяется
по
формуле

где
p1 и
p0 –
цена
за
единицу
продукции
в
текущем
и
базисном
периодах.
Соответственно
определяются
индексы
себестоимости
и
затрат
рабочего
времени
по
каждому
виду
продукции.
Агрегатный
индекс
цен определяет
среднее
изменение
цены
р
по
совокупности
определенных
видов
продукции
q.
Для
характеристики
среднего
изменения
цен
на
потребитель-ские
товары
используют
индекс
цен,
предложенный Э.
Ласпейресом
(индекс
Ласпейреса):

где
q0 –
потребительская
корзина
(базовый
период);
p0 и
p1 –
соответственно
цены
базисного
и
отчетного
периодов.
Если
количество
набора
продуктов
принимается
на
уровне
отчетного
периода
(q1 ),
то
в
этом
случае
индекс
цен
именуется индексом
Пааше:

Если
известны
индивидуальные
индексы
цен
по
отдельным
видам
продукции
и
стоимость
отдельных
видов
продукции,
то
применяются
средние
взвешенные
индексы
цен
(средний
взвешенный
арифметический
и
средний
взвешенный
гармонический
индексы
цен).
Формула среднего
взвешенного
арифметического
индекса
цен

где
i – индивидуальный
индекс
по
каждому
виду
продукции;
p0 q0 –
стоимость
продукции
каждого
вида
в
базисном
периоде.
Формула среднего
взвешенного
гармонического
индекса
цен
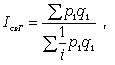
где
p1 q1 –
стоимость
продукции
каждого
вида
в
текущем
периоде.
В
статистической
практике
очень
широко
используется
агрегатный
территориальный
индекс
цен,
который
может
быть
рассчитан
по
следующей
формуле:
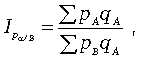
где
pA pB –
цена
за
единицу
продукции
каждого
вида
соответственно
на
территории
А
и
В;
qA –
количество
выработанной
или
реализованной
продукции
каждого
вида
по
территории
А
(в
натуральном
выражении).
Из
формулы
видно,
что
в
данном
индексе
в
качестве
фиксированного
показателя
(веса)
принят
объем
продукции
территории
А.
При
расчете
данного
индекса
в
качестве
веса
можно
принять
также
объем
продукции
территории
В
или
суммарный
объем
продукции
двух
территорий.
Возможны
два
способа
расчета
индексов:
цепной
и
базисный.
Цепные
индексы получают
путем
сопоставления
текущих
уровней
с
предшествующим,
при
этом
база
сравнения
постоянно
меняется.
Базисные
индексы получают
путем
сопоставления
с
тем
уровнем
периода,
который
был
принят
за
базу
сравнения.
В
качестве
примера
можно
привести
цепные
и
базисные
индексы
цен.
Цепные
индивидуальные
индексы
цен имеют
следующий
ряд
расчета:
…
. (10.15)
Базисные
индивидуальные
индексы
цен:
…
. (10.16)
Следует
помнить,
что
произведение
цепных
индивидуальных
индексов
цен
равно
последнему
базисному
индексу:
(10.17)
Цепные
агрегатные
индексы
цен:

. (10.18)
Базисные
агрегатные
индексы
цен:
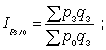
. (10.19)
Между
индексами
существует
также
взаимосвязь
и
взаимозависимость,
как
и
между
самими
экономическими
явлениями,
что
позволяет
проводить
факторный
анализ.
Благодаря
индексному
методу
можно
рассматривать
все
факторы
независимо
друг
от
друга,
что
дает
возможность
определить
размер
абсолютного
изменения
сложного
явления
за
счет
каждого
фактора
в
отдельности.
Предположим,
что
результативный
признак
зависит
от
трех
факторов
и
более.
В
этом
случае результативный
индекс примет
вид
(10.20)
Изменение
результативного
индекса
за
счет
каждого
фактора
может
быть
выражено
следующим
образом:

(10.21)
Для
выявления
роли
каждого
фактора
в
отдельности
индекс
сложного
показателя
разлагают
на
частные
(факторные)
индексы,
которые
характеризуют
роль
каждого
фактора.
При
этом
используют
два
метода:
-
метод
обособленного
изучения
факторов; -
последовательно-цепной
метод.
При
первом
методе
сложный
показатель
берется
с
учетом
изменения
лишь
того
фактора,
который
взят
в
качестве
исследуемого,
все
остальные
остаются
неизменными
на
уровне
базисного
периода.
Последовательно-цепной
метод
предполагает
использование
системы
взаимосвязанных
индексов,
которая
требует
определенного
расположения
факторов.
Как
правило,
на
первом
месте
в
цепи
располагают
качественный
фактор.
При
определении
влияния
первого
фактора
все
остальные
сохраняются
в
числителе
и
знаменателе
на
уровне
базисного
периода,
при
определении
второго
факторного
индекса
первый
фактор
сохраняется
на
уровне
базисного
периода,
а
третий
и
все
последующие
– на
уровне
отчетного
периода,
при
определении
третьего
факторного
индекса
первый
и
второй
факторы
сохраняются
на
уровне
базисного
периода,
четвертый
и
все
остальные
– на
уровне
отчетного
периода
и
т.д.
8.
Выборочное
наблюдение
относится
к
разновидности несплошного
наблюдения.
Оно
охватывает
отобранную
часть
единиц
генеральной
совокупности.
Цель
выборочного
наблюдения
– по
отобранной
части
единиц
дать
характеристику
всей
совокупности
единиц.
Чтобы
отобранная
часть
была
репрезентативна
(т.е.
представляла
всю
совокупность
единиц),
выборочное
наблюдение
должно
быть
специально
организовано.
Следовательно,
в
отличие
от
генеральной
совокупности,
представляющей
всю
совокупность
исследуемых
единиц,
выборочная
совокупность
представляет
ту
часть
единиц
генеральной
совокупности,
которая
является
объектом
непосредственного
наблюдения.
По
понятным
причинам
выборочный
метод
может
широко
использоваться
органами
государственной
статистики.
Он
позволяет
при
значительной
экономии
средств
и
затрат
получать
необходимую
достоверную
информацию.
Гарантия
репрезентативности
обеспечивается
применением
научно
обоснованных
способов
отбора
единиц,
которые
подлежат
обследованию.
Следует
сразу
же
иметь
в
виду,
что
при
сопоставлении
показателей
по
результатам
выборочного
исследования
с
характеристиками
для
всей
генеральной
совокупности
могут
иметь
место
отклонения.
Величина
этих
отклонений
называется
ошибкой
наблюдения,
которая
может
быть
или ошибкой
регистрации(несовершенство
технических
условий),
или ошибкой
репрезентативности (случайное
или
систематическое
нарушение
правил
при
отборе
единиц).
В
статистике
приняты
следующие
условные
обозначения:
N
– объем
генеральной
совокупности;
п
– объем
выборочной
совокупности;
–
средняя
в
генеральной
совокупности;
–
средняя
в
выборочной
совокупности;
р
– доля
единиц
в
генеральной
совокупности;
w
– доля
единиц
в
выборочной
совокупности;
–
генеральная
дисперсия;
S2 –
выборочная
дисперсия;
–
среднее
квадратическое
отклонение
признака
в
генеральной
совокупности;
S
– среднее
квадратическое
отклонение
признака
в
выборочной
совокупности.
11.2.
Виды
выборки,
способы
отбора
и
ошибки
выборочного
наблюдения
По
способу
отбора
(способу
формирования)
выборки
единиц
из
генеральной
совокупности
распространены
следующие
виды выборочного
наблюдения:
-
простая
случайная
выборка
(собственно-случайная); -
типическая
(стратифицированная); -
серийная
(гнездовая); -
механическая;
-
комбинированная;
-
ступенчатая.
Простая
случайная
выборка
(собственно–случайная) есть
отбор
единиц
из
генеральной
совокупности
путем
случайного
отбора,
но
при
условии
вероятности
выбора
любой
единицы
из
генеральной
совокупности.
Отбор
проводится
методом
жеребьевки
или
по
таблице
случайных
чисел.
Типическая
(стратифицированная)
выборка предполагает
разделение
неоднородной
генеральной
совокупности
на
типологические
или
районированные
группы
по
какому-либо
существенному
признаку,
после
чего
из
каждой
группы
производится
случайный
отбор
единиц.
Для серийной
(гнездовой)
выборки характерно
то,
что
генеральная
совокупность
первоначально
разбивается
на
определенные
равновеликие
или
неравновеликие
серии
(единицы
внутри
серий
связаны
по
определенному
признаку),
из
которых
путем
случайного
отбора
отбираются
серии
и
затем
внутри
отобранных
серий
проводится
сплошное
наблюдение.
Механическая
выборка представляет
собой
отбор
единиц
через
равные
промежутки
(по
алфавиту,
через
временные
промежутки,
по
пространственному
способу
и
т.д.).
При
проведении
механического
отбора
генеральная
совокупность
разбивается
на
равные
по
численности
группы,
из
которых
затем
отбирается
по
одной
единице.
Комбинированная
выборка основана
на
сочетании
нескольких
способов
выборки.
Многоступенчатая
выборка есть
образование
внутри
генеральной
совокупности
вначале
крупных
групп
единиц,
из
которых
образуются
группы,
меньшие
по
объему,
и
так
до
тех
пор,
пока
не
будут
отобраны
те
группы
или
отдельные
единицы,
которые
необходимо
исследовать.
Выборочный
отбор
может
быть
повторным
и
бесповторным.
При повторном
отборе вероятность
выбора
любой
единицы
не
ограничена.
При бесповторном
отборе выбранная
единица
в
исходную
совокупность
не
возвращается.
Для
отобранных
единиц
рассчитываются
обобщенные
показатели
(средние
или
относительные)
и
в
дальнейшем
результаты
выборочного
исследования
распространяются
на
всю
генеральную
совокупность.
Основной
задачей
при
выборочном
исследовании
является
определение
ошибок
выборки.
Принято
различать
среднюю
и
предельную
ошибки
выборки.
Для
иллюстрации
можно
предложить
расчет
ошибки
выборки
на
примере
простого
случайного
отбора.
Расчет средней
ошибки
повторной
простой
случайной
выборки производится
следующим
образом:
cредняя
ошибка
для
средней

cредняя
ошибка
для
доли

Расчет средней
ошибки
бесповторной
случайной
выборки:
средняя
ошибка
для
средней

средняя
ошибка
для
доли
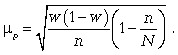
Расчет предельной
ошибки повторной
случайной
выборки:
предельная
ошибка
для
средней
предельная
ошибка
для
доли

где
t – коэффициент
кратности;
Расчет предельной
ошибки
бесповторной
случайной
выборки:
предельная
ошибка
для
средней

предельная
ошибка
для
доли

Следует
обратить
внимание
на
то,
что
под
знаком
радикала
в
формулах
при
бесповторном
отборе
появляется
множитель,
где
N – численность
генеральной
совокупности.
Что
касается
расчета
ошибки
выборки
в
других
видах
выборочного
отбора
(например,
типической
и
серийной),
то
необходимо
отметить
следующее.
Для типической
выборки величина
стандартной
ошибки
зависит
от
точности
определения
групповых
средних.
Так,
в
формуле
предельной
ошибки
типической
выборки
учитывается
средняя
из
групповых
дисперсий,
т.е.

При серийной
выборке величина
ошибки
выборки
зависит
не
от
числа
исследуемых
единиц,
а
от
числа
обследованных
серий
(s) и
от
величины
межгрупповой
дисперсии:
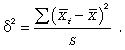
Серийная
выборка,
как
правило,
проводится
как
бесповторная,
и
формула
ошибки
выборки
в
этом
случае
имеет
вид
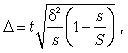
где -межсерийная
дисперсия;
s – число
отобранных
серий;
S – число
серий
в
генеральной
совокупности.
Все
вышеприведенные
формулы
применимы
для большой
выборки.
Кроме
большой
выборки
используются
так
называемые малые
выборки (n
< 30), которые
могут
иметь
место
в
случаях
нецелесообразности
использования
больших
выборок.
При
расчете
ошибок
малой
выборки
необходимо
учесть
два
момента:
1)
формула
средней
ошибки
имеет
вид

2)
при
определении
доверительных
интервалов
исследуемого
показателя
в
генеральной
совокупности
или
при
нахождении
вероятности
допуска
той
или
иной
ошибки
необходимо
использовать
таблицы
вероятности Стьюдента,
где
Р
= S (t, n), при
этом
Р
определяется
в
зависимости
от
объема
выборки
и
t.
В
статистических
исследованиях
с
помощью
формулы
предельной
ошибки
можно
решать
ряд
задач.
1.
Определять
возможные
пределы
нахождения
характеристики
генеральной
совокупности
на
основе
данных
выборки.
Доверительные
интервалы
для
генеральной
средней можно
установить
на
основе
соотношений
(11.12)
где
– генеральная
и
выборочная
средние
соответственно; -предельная
ошибка
выборочной
средней.
Доверительные
интервалы
для
генеральной
доли устанавливаются
на
основе
соотношений
(11.13)
2.
Определять
доверительную
вероятность,
которая
означает,
что
характеристика
генеральной
совокупности
отличается
от
выборочной
на
заданную
величину.
Доверительная
вероятность
является
функцией
от
t, где
(11.14)
Доверительная
вероятность
по
величине
t определяется
по
специальной
таблице.
3.
Определять
необходимый
объем
выборки
с
помощью
допустимой
величины
ошибки:
(11.15)
Чтобы
рассчитать
численность
п
повторной
и
бесповторной
простой
случайной
выборки,
можно
использовать
следующие
формулы:
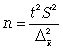
средней
при
повторном
способе);
(11.16)
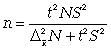
средней
при
бесповторном
способе);
(11.17)

доли
при
повторном
способе);
(11.18)

доли
при
бесповторном
способе).
(11.19)
9.
Методы многомерного статистическогоанализа
Методы математической статистики, используемые для построения оптимальных планов сбора,систематизации и обработки многомерных статистических данных, направленные на выявление характера иструктуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенные дляполучения научных и практических выводов.
По содержанию Мм.с.а. могут быть условно разделены на три основные группы:
1) Мм.с.а. многомерных распределений и их основных характеристик;
2) Мм.с.а. характера и структуры взаимосвязей между компонентами исследуемого многомерногопризнака;
3) М.м.с.а. геометрической структуры исследуемой совокупности многомерных наблюдений.
Методы первой группы охватывают лишь те ситуации, в которых обрабатываемые наблюдения имеютвероятностную природу, т. е. интерпретируются как выборка из соответствующей генеральной совокупности.К основным задачам этого подраздела относятся: статистическое оценивание исследуемых многомерныхраспределений, их основных числовых характеристик и параметров, исследование распределениявероятностей для ряда статистик, с помощью которых строятся статистические критерии проверки различныхгипотез о вероятностной природе анализируемых многомерных данных. Вторая группа методов объединяет всебе понятия и результаты, обслуживающие такие методы и модели математического статистическогоанализа, как множественная регрессия, многомерный дисперсный анализ, факторный анализ и др.Результаты данных методов могут быть условно разделены на два основных типа: а) построение наилучшихстатистических оценок для параметров этих моделей и анализ их свойств (точности, а в вероятностнойпостановке – законов их распределения, доверительных областей и т. д.); б) построение статистическихкритериев для проверки различных гипотез о структуре исследуемых взаимосвязей. Третья группа -объединяет в себе понятия и результаты таких моделей и схем, как дискриминантный анализ, анализмногомерного шкалирования. Узловым во всех этих схемах является понятие расстояния (меры близости,меры сходства) между анализируемыми элементами. При этом анализируемыми могут быть как реальныеобъекты, так и сами показатели.
Прикладное назначение М. м. с.а. состоит в основном в обслуживании трех проблем:
1) проблема статистического исследования зависимостей между анализируемыми показателями;
2) проблема классификации элементов (объектов или показателей) в общей (нестрогой) постановке, чтобывсю анализируемую совокупность элементов, статистически представленную в виде матрицы, разбить насравнительно небольшое число однородных групп;
3) проблема снижения размерности исследуемого факторного пространства и отбора наиболееинформативных показателей.
♦ методы анализа социолингвистических исследований
Среднегодовой темп роста применяется при анализе рядов динамики для выявления общей тенденции изменения показателя во времени.
Как видно из названия – это усредненный показатель. Его значение говорит о том, что если бы каждый год темп роста был одинаковым и равен среднему, то общий рост показателя был равен фактическому.
Среднегодовой темп роста можно определить двумя способами:
- Tp‾=yny1n−1∗100%overline{T_p}=sqrt[n-1]{frac{y_n}{y_1}}*100%,
где yny_n — значение показателя отчетного периода;
y1y_1 — значение показателя базового периода;
nn — количество лет.
- Tp‾=Kp2∗Kp3∗…∗Kpnn−1∗100%overline{T_p}=sqrt[n-1]{K_p^2*K_p^3*…*K_p^n}*100%,
где KpiK_p^i — цепной коэффициент роста за i-й период.
Примеры решения задач
Пример 1
В 2010 году на предприятии было выпущено продукции на 3650 тыс. руб., а в 2017 — на 4251 тыс. руб. Найти среднегодовой темп роста выпуска продукции.
Решение
Tp‾=425136508−1∗100%=102,2%overline{T_p}=sqrt[8-1]{frac{4251}{3650}}*100%=102,2%
В среднем за год выпуск продукции возрастал на 2,2%.
Ответ: Tp‾=102,2%overline{T_p}=102,2%
Пример 2
Рассчитать среднегодовой темп роста с использованием коэффициентов роста.
| Год | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Объем выпуска, тыс. шт. | 1020 | 1021 | 1300 | 1250 | 1280 | 1310 | 1390 | 1460 |
Решение
Решим данную задачу средствами MS Excel.
Коэффициент роста определяется как отношение показателя текущего года к предыдущему.
Получаем
Далее необходимо получить произведение этих коэффициентов.
Извлекаем корень 7-й степени. Это возможно двумя путями
Или
Также среднегодового темпа роста при помощи средней геометрической
Получили
Ответ: 105,26%.
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Темп роста
Вычисление темпа роста начинается с определения ряда чисел, между какими нужно найти процентное соотношение. Контрольное число обычно сравнивают или с предыдущим показателем, или с базовым, стоящим в начине числового ряда. Итог выражается в процентах.
Формула темпа роста выглядит следующим образом:
Темп роста = Льющийся показатель/Базовый показатель*100%. Если итог получается больше 100% — отмечается рост. Соответственно, меньше 100 – снижение.
Образцом можно использовать вариант роста и снижения заработной платы. Сотрудник получал зарплату помесячно: в январе – 30 000, в феврале – 35 000. Темп роста составил:
35 000 / 30 000 * 100 = 116,66. В феврале сравнительно января зарплата составила 116%.
Общая характеристика
Часто 2 показателя сравнивают, но каждый из них имеет особенности и предназначение для анализа. Рассчитать темп роста и прироста можно с помощью формул.
Понятие и предназначение
Вычисление темпа роста (ТР) осуществляется с поиска чисел, между которыми находят соотношение процентов. Это значит, что контрольное число сравнивают с прошлым, базисным показателем. Конечная сумма должна выражать процентную величину, которая позволяет проанализировать динамику показателей.
ТР = Текущая величина/Базовая величина*100%.
Когда итоговая сумма получается более 100%, происходит рост коэффициентов, а при цифрах ниже 100 — снижение. Формула расчета темпа роста в процентах показывает, во сколько раз новое значение отличается от предыдущего или постоянного базисного. Показатель ТР может определяться как увеличение, рост, сокращение уровня.
Данные темпа прироста (ТП) — это отражение, насколько поднялось или снизилось значение за установленное время. Показывается конкретная цифра, позволяющая судить о результатах деятельности в динамике по разным отраслям. Высчитывая отношение заработной платы или прочих параметров по формуле величины ТП, определяют, на сколько процентов поменялась эта сумма.
Темп прироста = (Текущее значение — базовое значение)/ базовое значение*100%.
Два варианта расчета являются тождественными. Отрицательный результат сообщает о снижении значения за анализируемый период. Всегда измеряется в процентах. ТП считается через коэффициент роста, ТР или через значения, являющиеся исходными данными и участвующие при расчетах.
Для определения среднего или среднегодового темпа роста (СГТР) складывают цифры за все сроки и делят полученную сумму на количество периодов. Также рассчитывается средний темп прироста.
Среднемесячный ТР и ТП применяется для определения усредненной величины изменения показателей за год или другой срок.
Средние показатели:
- ТР = корень в степени n Y 1/ Y 0.
- ТП = средний темп роста — 100.
Можно определить ТР экспорта и импорта объема производства, выпуска продукции, численности населения или прочих показателей. Можно вычислить годовую, средневзвешенную цену — отношение объема оборота текущего периода к показателям за год. Можно установить ТР по заболеваемости в стране, используя расчеты. Чаще всего может применяться к одному временному периоду — году.
Основные вычисления
В отчетах статистики и анализа часто используются показатели, измеряющиеся в процентах. Они также характеризуют, насколько изменилось значение величины за определенный период времени.
Методы расчета:
- цепной;
- базисный.
В программе Excel на примере наглядно виден способ расчета с помощью базисного и цепного ТР, ТП.
Чтобы рассчитать базисный ТР, нужно произвести расчет темпов роста всех показателей. ТР и ТП первого показателя не должен считаться. За базисную величину принимают Показатель 1, поэтому базовые ТР и ТП должны рассчитываться исходя из этого положения. При расчете Показатель (П)2 делится на Показатель 1 и умножается на 100, затем П3 делится на П1 и умножается на 100.
В расчет цепного темпа роста (ЦТР) используются все показатели, кроме первого. Способ вычисления отличается тем, что Показатель 2 делится на П1, умножается на 100. Затем П3 делят на П2 и умножают на 100. База вычисления — основной показатель. П4 делят на П3 и умножают на 100, при расчете ЦТП из каждого показателя ЦТР вычитают 100.
При расчете базисного и цепного показателей значения ТР и прироста будут равными, потому что при избрании в качестве показателя первого из ряда, они рассчитываются одинаково.
Рассчитывается абсолютный прирост, как разница между двумя величинами. Цепной и базисный ТР имеет взаимосвязь: произведение ЦТР равно базисному ТР за весь период.
Между двумя значениями имеется прямая зависимость. Разница равна 100% и отражается в формуле ТП.
Практические навыки
ТР. показывает, сколько процентов составляет одно число от другого. С помощью ТП можно вычислить, на сколько процентов возросло или сократилось число относительно другого.
Использование формул
ТР не бывает отрицательным, а ТП может. ТП определяется на базе ТР, обратный порядок недопустим. Чтобы высчитать величину, применяется ПП, поскольку он наглядно отражает динамику изменений.
Эти параметры имеют большое значение для анализа и планирования показателей в науке, статистике, экономике и других сферах. Распространено их использование в оптимизации выручки от продажи, оплаты труда, товарооборота, денежной наличности.
Можно на примере посчитать темп роста в процентах. Работник завода получал заработную плату каждый месяц в зависимости от выработки. В январе сотрудник получил 40000 рублей, в феврале 45000 р. ТР составляет по формуле: 45000/40000*100 = 112,5. Таким образом, в феврале доход относительно предыдущего месяца может исчисляться как 112%.
Формулы широко применяются в повседневной жизни населения. В интернете имеется онлайн-калькулятор, позволяющий получить реальный результат или проверить собственные решения. Их использование позволяет опустить ошибки расчетов.
Разные методы расчета
Наглядное использование формул на примере позволит проанализировать предназначение ТР и ТП. В таблице представлен внутренний валовой продукт России с 2010—2017 годы. Необходимо найти ТР (в процентах) базисным и цепным методами.
Таблица данных о ВВП в национальной валюте за 2011−2018 гг.
| Период | ВВП России ТР | (%) | |
| в млрд р. | Цепной метод | Базисный метод | |
| 2011 | 48 000 | — | — |
| 2012 | 57 698 | 120,2 | 120,2 |
| 2013 | 66 817 | 115,8 | 139,2 |
| 2014 | 71 117 | 106,4 | 148,2 |
| 2015 | 78 945 | 111,0 | 164,5 |
| 2016 | 80 826 | 102,4 | 168,4 |
| 2017 | 83 871 | 103,8 | 174,7 |
| 2018 | 88 177 | 105,1 | 183,7 |
Формула цепного метода: ТР= Yi / Yi -1*100.
Для 2011 величины не будет. Начиная с 2012 года: 57698/48000*100 = 120,2%. Для 2013 года: 66817/57698*100 = 115,8%. Таким способом высчитываются суммы для каждого периода.
Базисный метод: ТР = Yi/Ybasic*100. Это отношение к основному, первому коэффициенту. Например, для 2012 года суммы высчитываются 57698/48000*100 = 120,2%, для 2013 года: 66817/48000*100 = 115,8%. Таким принципом вычисляются все оставшиеся периоды.
Таким же способом рассчитывается процентное соотношение данных актива баланса, отчета о прибылях и убытках. Показатели, отражающие величину чистой прибыли за 2 года, позволят выявить прирост или снижение показателей.
| Данные | 2017 | 2018 | ТР % |
| Выручка от реализации | 1500000 | 1600000 | 106,7 |
| Финансовые доходы | 400000 | 350000 | 87,5 |
За 2018 год ТР составит 106,7% выручки, а доходы от вложений возросли на 87,5%.
ТР необходим, чтобы узнать, сколько процентов составляет одно значение от другого. Последним выступает предыдущее число. Темп прироста позволяет выяснить, насколько изменился заданный параметр.
На основе одного из коэффициентов нельзя составить верную оценку определяемому явлению (по международному, отечественному рынку, предприятию, показателю работоспособности фирмы). Необходимы комплексные меры изучения и расчетов показателей в динамике. Для анализа финансовой деятельности можно брать разную информацию из форм отчетности.
Примеры решения задач
| Задание | Для предприятия ООО «Севермет» даны следующие показатели, представленные за 2015 и 2016 год: |
2015 год – 120млн. рублей,
2016 год – 110,4млн. рублей.
Известно, что в 2017 году величина дохода увеличилась в сравнении с 2016 годом на 25 млн. рублей.
На основе имеющихся данных рассчитать темп роста и прироста, сделав при этом выводы.
Решение Определим темп роста в процентах за 2015 и 2016 год, для чего нужна формула темпа роста:
Здесь Тр – темп роста,
П2015 – показатель за 2015 год,
П2016 – показатель за 2016 год.
Тр=110,4млн. руб./120млн. руб. * 100% = 92 %
Темп прироста обозначает процентное соотношение изменения величины в текущем периоде в сравнении с предыдущим. Для расчета нужна формула темпа прироста:
Или второй способ:
Рассчитаем показатели за 2017 год
Тр=(120 млн. руб. + 25 млн. руб.)/120 млн. руб.= 1,21 (или 121 %)
Тп=(145 млн. руб./120 млн. руб)-1=0,208 (или 20,8%)
Вывод. Мы видим, что темп роста при сравнении 2015 и 2016 года составил 92%. Это означает, что прибыль предприятия в 2016 году уменьшилась на 92%в сравнении с 2015 годом. При расчете темпа прироста получилась отрицательная величина (-8%), что говорит о том, что прибыль компании в 2016 году (при сравнении с 2015 годом) уменьшилась на 8%. В 2017 году прибыль составила 121% в сравнении с 2016 годом. При расчете темпа прироста мы видим, что он составил 20,8%. Положительная величина говорит об увеличении прибыли именно на это количество процентов.
Ответ При сравнении 2015 и 2016 года Тр=92 %, Тп=8%, при сравнении 2016 и 2017 года Тр=121%, Тп=20,8%.
| Задание | Рассчитать прирост заработной платы на предприятии ООО «Севермет» за 2015 и 2016 год. Даны следующие показатели: |
Заработная плата 2015 год – 31,5 тыс. руб.,
заработная плата 2016 год – 33 тыс. руб.,
Решение Темп прироста обозначает процентное соотношение изменения величины в текущем периоде в сравнении с предыдущим. Для расчета нужна формула:
Вывод: Таким образом, мы видим, что темп прироста составил 4,8 %, что означает, что заработная плата в 2016 году по сравнению с 2015 годом увеличилась на 4,8%.
Средний годовой темп роста и средний годовой темп прироста
Прежде всего отметим, что приведенные в таблице темпы роста ( гр.7 и 8) являются рядами динамики относительных величин — производными от интервального ряда динамики (гр.2). Ежегодные темпы роста (гр.7) изменяются по годам ( 105%; 103,8%; 105,5%; 101,7%). Как вычислить среднюю величину из ежегодных темпов роста ? Эта величина называется среднегодовым темпом роста.
Среднегодовой темп роста исчисляется в следующей последовательности:
сначала по формуле средней геометрической исчисляют среднегодовой коэффициент роста (снижения) —
2. на базе среднегодового коэффициента определяют среднегодовой темп роста (
) путем умножения коэффиицента на 100%:
Среднегодовой темп прироста (
определяется путем вычитания из темпа роста 100%.
Среднегодовой коэффициент роста ( снижения ) по формулам средней геометрической может быть исчислен двумя способами:
на базе абсолютных показателей ряда динамики по формуле:
§ n — число уровней;
§ n — 1 — число лет в период;
на базе ежегодных коэффициентов роста по формуле
§ m — число коэффициентов.
Результаты расчета по формулам равны, так как в обеих формулах показатель степени — число лет в периоде, в течение которого происходило изменение. А подкоренное выражение — это коэффициент роста показателя за весь период времени (см. табл. 11.5, гр.6, по строке за 1998 г.).
Среднегодовой темп роста равен
Среднегодовой темп прироста определяется путем вычитания из среднегодового темпа роста 100%. В нашем примере среднегодовой темп прироста равен
Следовательно, за период 1995 — 1998 гг. объем производства продукта «А» в среднем за год возрастал на 4,0%. Ежегодные темпы прироста колебались от 1,7% в 1998 г. до 5,5% в 1997 г. (за каждый год темпы прироста см. в табл. 11.5, гр. 9).
Среднегодовой темп роста (прироста) позволяет сравнивать динамику развития взаимосвязанных явлений за длительный период времени (например, среднегодовые темпы роста численности работающих по отраслям экономики, объема производства продукции и др.), сравнивать динамику какого-либо явления по разным странам, исследовать динамику какого-либо явления по периодам исторического развития страны.
Формулы роста и прироста: базисный, цепной и посредственный
Темп роста и прироста могут быть найдены несколькими способами в зависимости от целей вычислений. Выделяют формулы получения базисного, цепного и посредственного темпа роста и прироста.
Базисный темп роста и прироста показывает отношение выбранного показателя ряда к показателю, зачисленному за основной (база вычисления). Обычно он находится в начале ряда. Формулы для вычисления следующие:
- Темп роста (Б) = Избранный показатель/Базовый показатель*100%;
- Темп прироста (Б) = Выбранный показатель/Базовый показатель*100%-100.
Цепной темп роста и прироста демонстрирует изменение показателя в динамике по цепочке. То есть отличие каждого последующего показателя по времени к предыдущему. Формулы выглядят так:
- Темп роста (Ц) = Избранный показатель/Предшествующий показатель*100%;
- Темп прироста (Ц) = Выбранный показатель/Предшествующий показатель*100%-100.
Между цепным и базисным темпом роста есть взаимосвязь. Отношение итога деления текущего показателя на базисный к итогу деления предыдущего показателя на базисный равновелик цепному темпу роста.
Средний темп роста и прироста используется для определения усредненной величины изменения показателей за год или иной отчетный период. Для того чтобы определить данную величину, нужно определить среднюю геометрическую от всех показателей в этапе либо найти путем определения отношения конечной величины к начальной:
- Средний темп роста
- Средний темп прироста = посредственный темп роста – 100.
Как рассчитать темп прироста
Он рассчитывается несколькими способами, самое простое рассчитать показатель на основе темпа роста путем вычитания 100. Разберем на тех же примерах, что выше.
Пример №1.2
Темп прироста = 33000/31500 * 100 — 100= 104,76-100 = 4,76%. Таким образом, средняя заработная плата выросла на 4,76% (+4,76%).
Пример №2.2
Темп прироста = 139000/142000 *100 -100 = 97,89-100 = -2,11%. Значение получилось с минусом, а значит темп снижения прибыль составил 2,11% или проще говоря прибыль отчетного года снизилась на 2,11% по сравнению с прибылью 2015 года.
Как еще можно посчитать темп прироста?
Если в задании вы рассчитывали абсолютное отклонение, то можно воспользоваться данным значение и разделить его на значение базисного года, рассмотрим на примере №1.1
Абсолютное отклонение = 33000 – 31 500 = 1500 рублей.
Темп прироста =1500 / 31500 * 100%= 4,76%. Мы видим, что от смены метода расчёта итог остался неизменным, поэтому выбирайте тот способ, который вам больше нравится.
Вернемся к теме статьи, и обобщим, в чем разница между темпом роста и прироста. Разница между показателями заключается в следующем:
- Методика расчёта.
- Темп роста показывает сколько процентов один показатель составляется относительно другого, а темп прироста говорит насколько он вырос.
- На базе темпа роста рассчитывают темп прироста, но не рассчитывают наоборот.
- Темп роста не может принимать отрицательное значение, а темп прироста может быть как положительным, так и отрицательным.
Если после прочтения материала вам непонятно, как рассчитать показатель или у вас остались вопросы по теме – задайте их в комментариях, не стесняйтесь.
Подсчет процентов в табличном редакторе
Табличный редактор хорош тем, что большую часть вычислений он производит самостоятельно, а пользователю необходимо ввести только исходные значения и указать принцип расчета. Вычисление производится так: Часть/Целое = Процент. Подробная инструкция выглядит так:
При работе с процентной информацией ячейке необходимо задать соответствующий формат.
- Жмем на необходимую ячейку правой клавишей мышки.
- В возникшем маленьком специальном контекстном меню необходимо выбрать кнопку, имеющую наименование «Формат ячеек».
Здесь необходимо щелкнуть левой клавишей мышки на элемент «Формат», а затем при помощи элемента «ОК», сохранить внесенные изменения.
Разберем небольшой пример, чтобы понять, как работать с процентной информацией в табличном редакторе. Подробная инструкция выглядит так:
У нас есть три колонки в табличке. В первой отображено наименование продукта, во второй – запланированные показатели, а в третьей – фактические.
В строчку D2 вводим такую формулу: =С2/В2.
Используя вышеприведенную инструкцию, переводим поле D2 в процентный вид.
Используя специальный маркер заполнения, растягиваем введенную формулу на всю колонку.
Готово! Табличный редактор сам высчитал процент реализации плана для каждого товара.
Нюансы вычислений
Представленные формулы очень похожи и могут вызывать затруднение и путаницу. Для этого поясним вытекающее:
- темп роста показывает, сколько процентов составляет одно число от другого;
- темп прироста показывает, на сколько процентов возросло или уменьшилось одно число относительно другого;
- темп роста не может быть отрицательным, темп прироста – может;
- темп прироста можно вычислить на базе темпа роста, возвратного порядка не допускается.
В экономической практике чаще используется показатель прироста, поскольку он более наглядно отражает динамику изменений.
Вычисление изменения в процентах при помощи формулы прироста
При помощи табличного редактора можно реализовать процедуру сравнения 2 долей. Для осуществления этого действия отлично подходит формула прироста. Если пользователю необходимо произвести сравнение числовых значений А и В, то формула будет иметь вид: =(В-А)/А=разница. Разберемся во всем более детально. Подробная инструкция выглядит так:
- В столбике А располагаются наименования товаров. В столбике В располагается его стоимость за август. В столбике С располагается его стоимость за сентябрь.
- Все необходимые вычисления будем производить в столбике D.
- Выбираем ячейку D2 при помощи левой клавиши мышки и вводим туда такую формулу: =(С2/В2)/В2.
- Наводим указатель в нижний правый уголок ячейки. Он принял форму небольшого плюсика темного цвета. При помощи зажатой левой клавиши мышки производим растягивание этой формулы на всю колонку.
- Если же необходимые значения находятся в одной колонке для определенной продукции за большой временной промежуток, то формула немножко изменится. К примеру, в колонке В располагается информация за все месяцы продаж. В колонке С необходимо вычислить изменения. Формула примет такой вид: =(В3-В2)/В2.
- Если числовые значения необходимо сравнить с определенными данными, то ссылку на элемент следует сделать абсолютной. К примеру, необходимо произвести сравнение всех месяцев продаж с январем, тогда формула примет такой вид: =(В3-В2)/$В$2. С помощью абсолютной ссылки при перемещении формулы в другие ячейки, координаты зафиксируются.
- Плюсовые показатели указывают на прирост, а минусовые – на уменьшение.
Расчет темпа прироста в табличном редакторе
Разберемся детально в том, как произвести расчет темпа прироста в табличном редакторе. Темп роста/прироста означает изменение определенного значения. Подразделяется на два вида: базисный и цепной.
Цепной темп роста обозначает отношение процента к предыдущему показателю. Формула цепного темпа роста выглядит следующим образом:
Базисный темп роста обозначает отношение процента к базисному показателю. Формула базисного темпа роста выглядит следующим образом:
Предыдущий показатель – это показатель в прошедшем квартале, месяце и так далее. Базисный показатель – это начальный показатель. Цепной тем прироста – это вычисляемая разница между 2 показателями (настоящий и прошлый). Формула цепного темпа прироста выглядит следующим образом:
Базисный темп прироста – это вычисляемая разница между 2 показателями (настоящий и базисный). Формула базисного темпа прироста выглядит следующим образом:
Рассмотрим все детально на конкретном примере. Подробная инструкция выглядит так:
К примеру, у нас есть такая табличка, отражающая доход по кварталам. Задача: вычислить темпы прироста и роста.
Первоначально реализуем добавление четырех колонок, в которых будут содержаться вышеприведенные формулы.
Мы уже выяснили, что такие значения высчитываются в процентах. Нам необходимо задать для таких ячеек процентный формат. Жмем на необходимый диапазон правой клавишей мышки. В возникшем маленьком специальном контекстном меню необходимо выбрать кнопку, имеющую наименование «Формат ячеек». Здесь необходимо щелкнуть левой клавишей мышки на элемент «Формат», а затем при помощи кнопки «ОК», сохранить внесенные изменения.
Вводим такую формулу для подсчета цепного темпа роста и копируем в нижние ячейки.
Вводим такую формулу для базисного цепного темпа роста и копируем в нижние ячейки.
Вводим такую формулу для подсчета цепного темпа прироста и копируем в нижние ячейки.
Вводим такую формулу для базисного цепного темпа прироста и копируем в нижние ячейки.
Готово! Мы реализовали подсчет всех необходимых показателей. Вывод по нашему конкретному примеру: в 3 квартале плохая динамика, так как темп роста составляет сто процентов, а прирост положительный.
Источники
- https://bankhys.ru/finansy/temp-rosta-i-temp-prirosta-opredeleni.html
- https://nauka.club/ekonomika/temp-rosta-i-temp-prirosta.html
- https://orto-ped.ru/chemu-raven-srednegodovoy-temp-prirosta-stoimosti-osnovnykh-sredstv-za-issleduyemyy-period/
- https://ya-prepod.ru/otlichie-tempa-rosta-ot-tempa-prirosta.html
- https://office-guru.ru/excel/formula-prirosta-v-procentah-v-excel.html
[свернуть]
Download Article
Download Article
The GDP is the Gross Domestic Product of a country or region over some chosen time period. This single figure represents the value (in local currency) of all of the goods and services produced within that region over a specific period of time.[1]
To understand whether the country’s economy is improving or declining, you may wish to calculate the annual growth rate of the GDP. This is a direct comparison of the GDP from one year to the next. If the result is positive, the economy is said to be improving. If negative, then the economy is declining. Growth rates can be compared annually or over shorter or longer time periods, depending on the research you are doing.
-
1
Determine the time period you want to calculate. The annualized GDP growth rate is a measure of the increase or decrease of the GDP from one year to the next. Understanding this measurement is a way of knowing whether the general economy for the country (or other chosen location) is getting better, worse or staying stable over time.[2]
- GDP figures are generally made available on a quarterly basis. To calculate the “annualized” GDP growth rate specifically, use data for the full year, not just a selected quarter.
- This figure is always called the “growth” rate and uses a single formula, regardless of whether the GDP is increasing or decreasing. If the value of the GDP increases from one year to the next, the formula will produce a positive result. If the result is negative, the value is dropping, and you can say that there has been “negative growth” over the selected time period.
- You can use it to compare the performance of a country to other countries.[3]
- But it has its limitations. Many economists suggest including measures of well-being among the current measurements to determine the absolute and relative success of a country.[4]
-
2
Collect the data from reliable government resources. In the United States, the accepted source for GDP data is the Bureau of Economic Analysis (BEA).[5]
The BEA is an agency of the U.S. Department of Commerce, which is charged with calculating the GDP for the United States. The BEA has the resources available to collect all the sales and employment data that becomes part of the GDP.[6]
- Visit the BEA website at http://www.bea.gov. From the home page, you can see numerous links to National GDP, Regional GDP, and a wide variety of press releases and data releases.
- For the annual GDP for the country, choose the link to “GDP.” You will be directed to a spreadsheet that contains the GDP, broken down by year and quarter for approximately the last 100 years.
Advertisement
-
3
Find the GDP for two consecutive years. To determine the annualized GDP growth rate, you need to know the GDP of two consecutive years. Using the data from the BEA, find the annual GDP for one year and the annual GDP for the next year.
-
4
Use the formula for growth rate. To calculate the growth rate over the chosen time period, use the formula:[7]
-
5
Interpret your result as a percentage. The growth rate formula provides you with a final result as a decimal number. To convert this to a percentage form that makes sense to economists, multiply by 100%. You can then report the annual growth rate as a percentage figure.[8]
- For example, again using the data from 2015 to 2016, the calculation produced a result of 0.02940. Convert this to a percentage as follows:
- Thus, you can report that the annualized growth rate of the U.S. GDP from 2015 to 2016 is 2.940%. Because the figure is positive, the GDP is improving over that time period.
- For example, again using the data from 2015 to 2016, the calculation produced a result of 0.02940. Convert this to a percentage as follows:
Advertisement
-
1
Collect the data for a chosen time period. A comparison of GDP growth rates does not have to be limited to annual data. In fact, economists often want to know results and see trends over smaller time periods.[9]
In the U.S., the BEA calculates and reports GDP data each quarter.[10]
- You can use and manipulate the data in any way you wish, as long as you define your calculations appropriately. For example, you might want to measure a short-term GDP growth from the third quarter of 2016 to the fourth quarter of 2016.
- Alternatively, you might want to compare the third quarter of 2015 to the third quarter of 2016. Note that, while this is a measure of data from two different years, this is not an annualized calculation. It is a comparison of a specific portion of each year, perhaps to determine whether the time of year has any impact on spending or production.
- Finally, someone studying long range changes in economies might even want to compare decades. For example, you could compare the GDP from 1980-1989 to the GDP from 1990-1999. You would do this by adding together the GDPs of the ten individual years.
-
2
Use the same percent change formula. Whether you want to calculate a growth rate over an annual range or for a shorter or longer time period, the formula remains the same. You find the difference of the two chosen time periods, divided by the GDP of the initial time period.[11]
-
3
Convert and interpret the result. Finally, use the figure that you obtain from the calculation and convert it to a percentage by multiplying by 100%. The result is the growth or decline of the GDP over your selected time period.[12]
- For the final two quarters of 2016, this calculation is:
- You would report that the GDP increased by 0.9933%, or almost 1% over the given two quarters.
- For the final two quarters of 2016, this calculation is:
Advertisement
-
1
Identify a location. The GDP is the gross domestic product of any identified geographic area. Usually, people measure and compare the GDP of individual countries. However, within the U.S., you might compare the GDP of separate states. On a broader scale, you may wish to find the GDP of North America or Asia.[13]
- Just as you need to define a location if you want to calculate GDP growth rates, you also need to understand what location is being represented when you read GDP data.
-
2
Select a method for measuring GDP. The GDP can be calculated in one of three different ways. Each method is valid but describes a slightly different approach to viewing the economy. When you calculate the GDP, you need to define which method you are using. The three methods are:[14]
- Expenditures approach. This method calculates the sum of expenditures by final consumers of products. The traditional formula when calculating GDP in this way is:
- GDP = Consumption + Investment + Gov’t Spending + (Exports – Imports)
- Income approach. Less commonly used, this method accounts for all the incomes earned and costs incurred in the country’s production.
- Value-added approach. This calculation measures the total sales of an area minus the value of services or supplies added during the course of production. This approach is regularly used in measuring U.S. industrial production.
- Expenditures approach. This method calculates the sum of expenditures by final consumers of products. The traditional formula when calculating GDP in this way is:
-
3
Research the data that comprises the GDP. The expenditures approach is the most direct calculation and the one most commonly used and studied by economists around the world. This calculation takes into account the following basic areas:
- Consumption. This first term accounts for personal consumption expenditures, which is basically the total amount of money that the population spends over the selected time period. The BEA breaks this down into two subcategories of goods and services. Goods are concrete items that can be bought and sold, and services are payments for other people’s labor or expertise.
- Investment. The investment figure constitutes the total of purchases that businesses make in the process of creating their products. This would include purchases of all supplies used in production as well as new equipment or machinery used to expand production. The investment category also includes materials used in residential construction projects.
- Government Spending. This item tracks what the government of the chosen region or country actually spends over the selected time period. Values are calculated at the prices that the government actually spends on items as diverse as office equipment, building supplies for government projects or weapons and items for the military.
- Net exports. Some formulas for GDP include a single term of “net exports,” while others will incorporate two terms, exports and imports. As long as both are included, the result will be the same. The calculation is to add all exports to the GDP and deduct the value of all imports. The net is the positive growth for the GDP.
-
4
Compile the data for the final calculation. The GDP, in basic terms, is the sum of the data that you calculated in the preceding step. When all the portions are determined, they are added to provide the final result.[15]
- For example, the BEA reports the following figures for the fourth quarter GDP of 2016 (figures are in billions of dollars):
- Consumption = $12,980.40
- Investment = $3,106.50
- Government = $3,312.10
- Net exports = -$538.30
- GDP = $18,860.70
- For example, the BEA reports the following figures for the fourth quarter GDP of 2016 (figures are in billions of dollars):
Advertisement
Add New Question
-
Question
Does GDP represent the overall success of a country?
Jonathan DeYoe is a Financial Advisor and the CEO of Mindful Money, a comprehensive financial planning and retirement income planning service based in Berkeley, California. With over 25 years of financial advising experience, Jonathan is a speaker and the best-selling author of “Mindful Money: Simple Practices for Reaching Your Financial Goals and Increasing Your Happiness Dividend.” Jonathan holds a BA in Philosophy and Religious Studies from Montana State University-Bozeman. He studied Financial Analysis at the CFA Institute and earned his Certified Private Wealth Advisor (CPWA®) designation from The Investments & Wealth Institute. He also earned his Accredited Investment Fiduciary (AIF®) credential from Fi360. Jonathan has been featured in the New York Times, the Wall Street Journal, Money Tips, Mindful Magazine, and Business Insider among others.
Author, Speaker, & CEO of Mindful Money
Expert Answer
The growth of GDP shows the economic success of a country. It has some limitations. Many economists suggest including measures of well-being among the current measurements to determine the absolute and relative success of a country.
-
Question
What does annualized GDP tell you about a country?
Jonathan DeYoe is a Financial Advisor and the CEO of Mindful Money, a comprehensive financial planning and retirement income planning service based in Berkeley, California. With over 25 years of financial advising experience, Jonathan is a speaker and the best-selling author of “Mindful Money: Simple Practices for Reaching Your Financial Goals and Increasing Your Happiness Dividend.” Jonathan holds a BA in Philosophy and Religious Studies from Montana State University-Bozeman. He studied Financial Analysis at the CFA Institute and earned his Certified Private Wealth Advisor (CPWA®) designation from The Investments & Wealth Institute. He also earned his Accredited Investment Fiduciary (AIF®) credential from Fi360. Jonathan has been featured in the New York Times, the Wall Street Journal, Money Tips, Mindful Magazine, and Business Insider among others.
Author, Speaker, & CEO of Mindful Money
Expert Answer
GDP is the value in local currency of all the goods and services produced within a specific geography (city, state, or country) over a specific period of time. It’s often used to provide a picture of how a country is doing compared to other countries and to itself over time.
-
Question
What if the GDP growth rates for two time periods are negative and the final rate is more negative than the initial?
Ed Rozmiarek
Community Answer
This would indicate a greatly declining economy. Apply the formula for calculating growth rate changes and just input the negative numbers that you have. Be careful with your calculations, so you don’t get confused when subtracting negative numbers.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
You can use a country’s GDP to get a picture of how that country is doing compared to other countries and to itself over time.[16]
Advertisement
References
- ↑ Jonathan DeYoe, CPWA®, AIF®. Author, Speaker, & CEO of Mindful Money. Expert Interview. 15 October 2020.
- ↑ Jonathan DeYoe, CPWA®, AIF®. Author, Speaker, & CEO of Mindful Money. Expert Interview. 15 October 2020.
- ↑ Jonathan DeYoe, CPWA®, AIF®. Author, Speaker, & CEO of Mindful Money. Expert Interview. 15 October 2020.
- ↑ Jonathan DeYoe, CPWA®, AIF®. Author, Speaker, & CEO of Mindful Money. Expert Interview. 15 October 2020.
- ↑ Jonathan DeYoe, CPWA®, AIF®. Author, Speaker, & CEO of Mindful Money. Expert Interview. 15 October 2020.
- ↑ https://www.bea.gov/
- ↑ https://www.omnicalculator.com/finance/gdp-growth
- ↑ https://www.omnicalculator.com/finance/gdp-growth
- ↑ Alex Kwan. Certified Public Accountant. Expert Interview. 1 June 2021.
About This Article
Article SummaryX
To calculate annualized GDP growth rates, start by finding the GDP for 2 consecutive years. Then, subtract the GDP from the first year from the GDP for the second year. Finally, divide the difference by the GDP for the first year to find the growth rate. Remember to express your answer as a percentage. To learn how to find or calculate GDP, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 243,034 times.
Reader Success Stories
-
R. Dwayne Allen
Sep 16, 2018
“What an outstanding article teaching the basic nuances of GDP formula to commute two years or more of growth…” more
Did this article help you?
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.



















































