Загрузить PDF
Загрузить PDF
Чтобы вычислить среднее арифметическое в группе чисел, необходимо их сложить и разделить на количество чисел. В повседневной жизни среднее арифметическое может пригодиться, когда необходимо оценить ежемесячные расходы, узнать, сколько времени уходит на выполнение той или иной задачи, или определить количество людей на основе предыдущего посещения.
-

1
Найдите сумму чисел в данном ряду. Первым делом сложите все числа в числовом ряду. Предположим, вам дан ряд 1, 2, 3, and 6. В этом случае сумма будет составлять
.[1]
-

2
Разделите результат на количество чисел в ряду. Наш ряд состоит из четырех чисел, поэтому следует взять сумму, 12, и разделить ее на четыре.[2]
. Среднее арифметическое в этом ряду равняется 3.[3]
Реклама
-

1
Запишите среднее арифметическое в каждой категории. Прежде всего найдите среднее арифметическое каждой категории, сложив все числа в ряду и разделив на количество чисел. Например, вам требуется найти средневзвешенное значение для класса и даны следующие числа:[4]
- Среднее арифметическое домашней работы = 93 %
- Среднее арифметическое экзамена = 88 %
- Среднее арифметическое проверочной работы = 91 %
-

2
Запишите весовую категорию каждого среднего арифметического. Помните, что весовые категории должны в сумме составлять 100 %. Предположим, вам даны следующие весовые категории:
- Среднее арифметическое домашней работы = 30 % итоговой оценки
- Среднее арифметическое экзамена = 50 % итоговой оценки
- Среднее арифметическое проверочной работы = 20 % итоговой оценки
-

3
-

4
Сложите полученные результаты. Чтобы найти средневзвешенное значение, сложите все три результата:
. Средневзвешенное значение для этого ряда равняется
.
Реклама
Советы
- Пользуйтесь бумагой и ручкой, они упрощают жизнь в миллион раз.
Реклама
Об этой статье
Эту страницу просматривали 73 270 раз.
Была ли эта статья полезной?
Допустим, что все значения
количественного признака X
совокупности,
безразлично-генеральной или выборочной,
разбиты на несколько групп. Рассматривая
каждую группу как самостоятельную
совокупность, можно найти ее среднюю
арифметическую.
Групповой средней называют среднее
арифметическое значений признака,
принадлежащих группе.
Теперь целесообразно ввести специальный
термин для средней всей совокупности.
Общей средней
![]() называют среднее
называют среднее
арифметическое значений признака,
принадлежащих всей совокупности.
Зная групповые средние и
объемы групп, можно найти общую среднюю:
общая средняя равна
средней арифметической групповых
средних, взвешенной по объемам групп,
Опуская доказательство, приведем
иллюстрирующий пример.
Пример.
Найти
общую среднюю совокупности, состоящей
из
следующих
двух групп:
|
Группа………………………. |
первая |
вторая |
||
|
Значение |
1 |
6 |
1 |
5 |
|
Частота……………………… |
10 |
15 |
20 |
30 |
|
Объем………………………. |
10+15 = 25 |
20 + 30 = 50 |
Решение.
Найдем групповые средние:
![]() =(10*1+15*6)/25=4;
=(10*1+15*6)/25=4;
![]() =
=
(20*1+30*5)/50
= 3,4.
Найдем общую
среднюю по групповым средним:
![]() =(25*
=(25*
4 + 50*3,4)/(25 + 50) = 3,6.
Замечание.
Для упрощения расчета общей средней
совокупности большого объема целесообразно
разбить ее на несколько групп, найти
групповые
средние и по ним общую среднюю.
§ 7. Отклонение от общей средней и его свойство
Рассмотрим совокупность,
безразлично-генеральную или выборочную,
значений количественного признака X
объема n:
значения признака .…… x1
x2
…
xk
частоты………………………
n1
n2
… nk
При
этом
![]() .
.
Далее
для удобства записи знак суммы
![]() заменен знаком
заменен знаком![]() .
.
Найдем общую среднюю:
![]() .
.
Отсюда
![]() .
.
(*)
Заметим, что поскольку x
– постоянная величина,
то
![]() .
.
(**)
Отклонением называют
разность
![]() между значением
между значением
признака и общей средней.
Теорема. Сумма
произведений отклонений на соответствующие
частоты равна нулю:
![]() .
.
Доказательство. Учитывая (*) и (**), получим
![]() .
.
Следствие. Среднее
значение отклонения равно нулю.
![]()
Пример.
Дано
распределение количественного признака
X:
xi
1
2 3
ni
10
4 6
Убедиться,
что сумма произведений отклонений на
соответствующие
частоты равна нулю.
Решение.
Найдем общую среднюю:
![]() =
=
(10*1+4*2+6*3)/20
=1,8
Найдем
сумму произведений отклонений на
соответствующие
частоты:
![]() .
.
§ 8. Генеральная дисперсия
Для того чтобы охарактеризовать
рассеяние значений количественного
признака X
генеральной совокупности
вокруг своего среднего значения, вводят
сводную характеристику – генеральную
дисперсию.
Генеральной дисперсией
Dг
называют среднее арифметическое
квадратов отклонений значений признака
генеральной совокупности от их среднего
значения ![]() .
.
Если все значения x1,
х2,
…, xN
признака генеральной
совокупности объема N
различны, то
 .
.
Если же значения признака
x1,
х2,
…, xk
имеют соответственно
частоты N1,
N2,…,
Nk,
причем N1
+N2+…+Nk=N,
то
 ,
,
т.е. генеральная дисперсия есть средняя
взвешенная квадратов отклонений с
весами, равными соответствующим частотам.
Пример.
Генеральная
совокупность задана таблицей распределения
xi
2
4
5 6
Ni
8
9 10 3
Найти генеральную
дисперсию.
Решение.
Найдем генеральную среднюю (см. § 3):
![]() .
.
Найдем генеральную
дисперсию;
![]() .
.
Кроме дисперсии для характеристики
рассеяния значений признака генеральной
совокупности вокруг своего среднего
значения пользуются сводной характеристикой
– средним квадратическим отклонением.
Генеральным средним
квадратическим отклонением (стандартом)
называют квадратный
корень из
генеральной дисперсии:
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти среднее и стандартное отклонение сгруппированных данных
17 авг. 2022 г.
читать 2 мин
Часто нам может понадобиться вычислить среднее значение и стандартное отклонение данных, которые каким-то образом сгруппированы. Например, предположим, что у нас есть следующие сгруппированные данные:
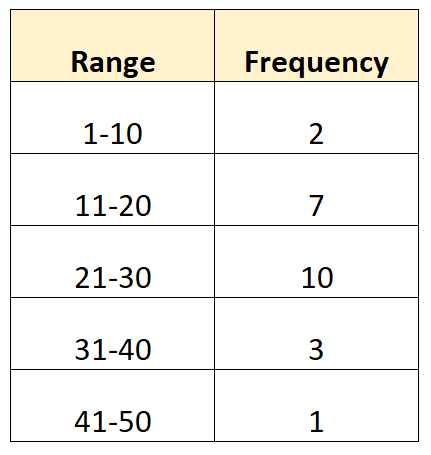
Хотя невозможно рассчитать точное среднее значение и стандартное отклонение, поскольку мы не знаем исходных значений данных , можно оценить среднее значение и стандартное отклонение.
Следующие шаги объясняют, как это сделать.
Связанный: Как найти режим сгруппированных данных
Вычислить среднее значение сгруппированных данных
Мы можем использовать следующую формулу для оценки среднего значения сгруппированных данных:
Среднее значение: Σm i n i / N
куда:
- m i : Середина i -й группы
- n i : Частота i -й группы
- N: общий размер выборки
Вот как мы могли бы применить эту формулу к нашему набору данных ранее:
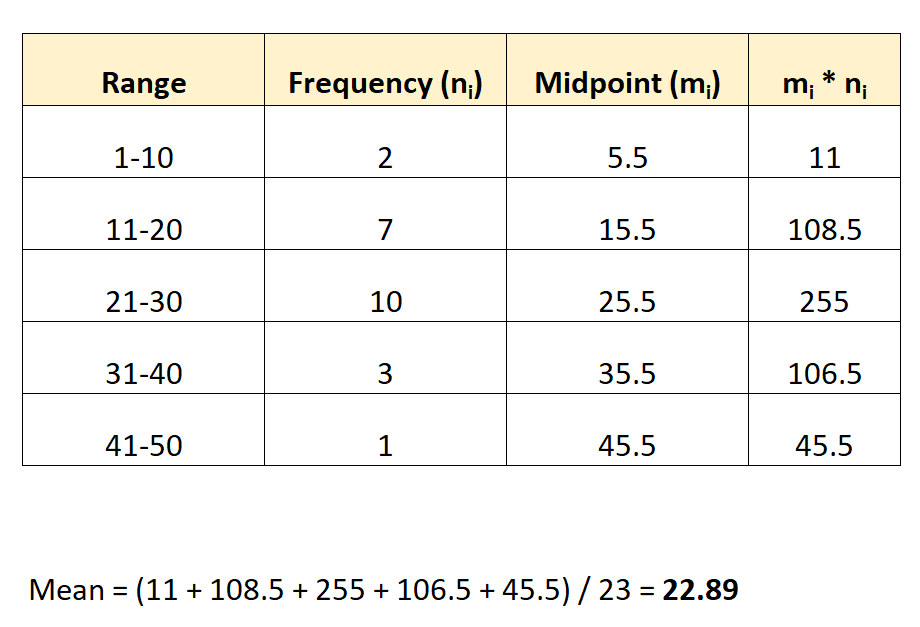
Среднее значение набора данных оказывается равным 22,89 .
Примечание. Среднюю точку для каждой группы можно найти, взяв среднее значение нижнего и верхнего значения диапазона. Например, средняя точка для первой группы рассчитывается как: (1+10)/2 = 5,5.
Вычислите стандартное отклонение сгруппированных данных
Мы можем использовать следующую формулу для оценки стандартного отклонения сгруппированных данных:
Стандартное отклонение: √ Σn i (m i -μ) 2 / (N-1)
куда:
- n i : Частота i -й группы
- m i : Середина i -й группы
- μ : среднее значение
- N: общий размер выборки
Вот как мы применим эту формулу к нашему набору данных:
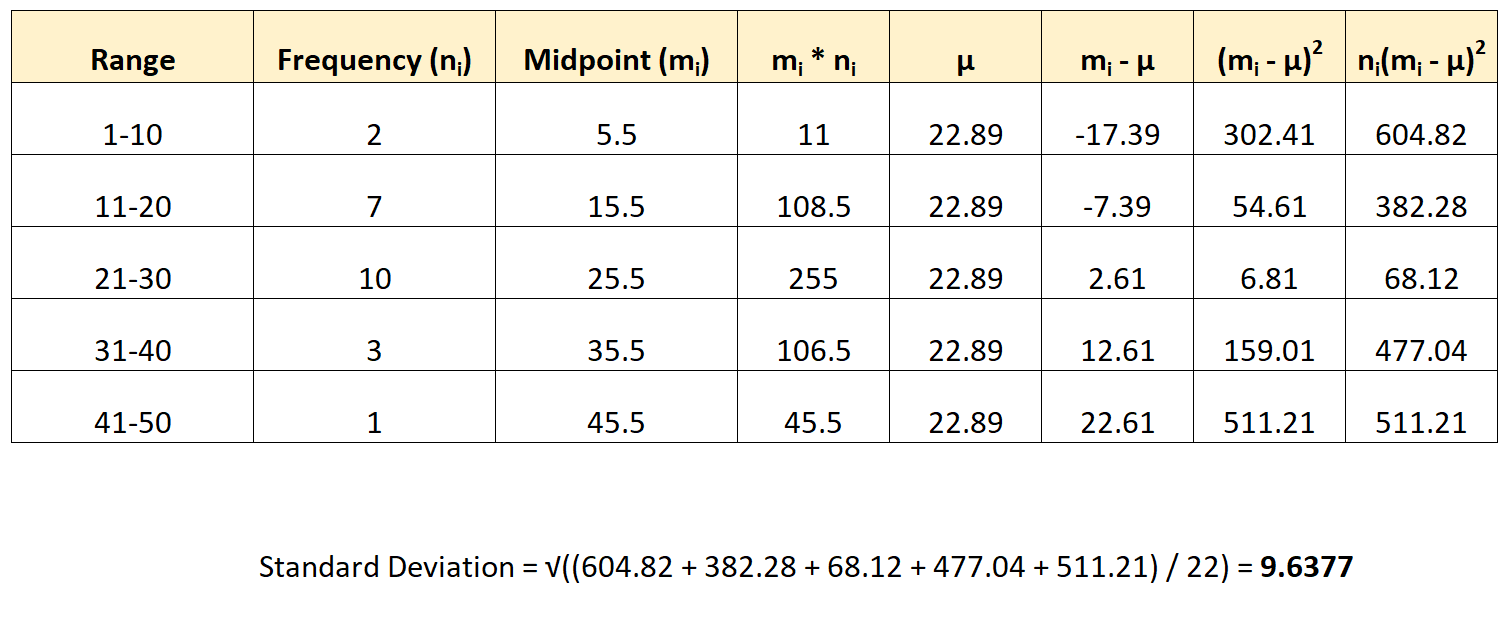
Стандартное отклонение набора данных оказывается равным 9,6377 .
Дополнительные ресурсы
Как оценить среднее значение и медиану любой гистограммы
Как рассчитать процентильный ранг для сгруппированных данных
Как найти медиану сгруппированных данных
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.

Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.

Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:

Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.

Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.

Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.

Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.

Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.

Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».

Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.
Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
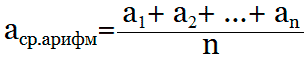
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

