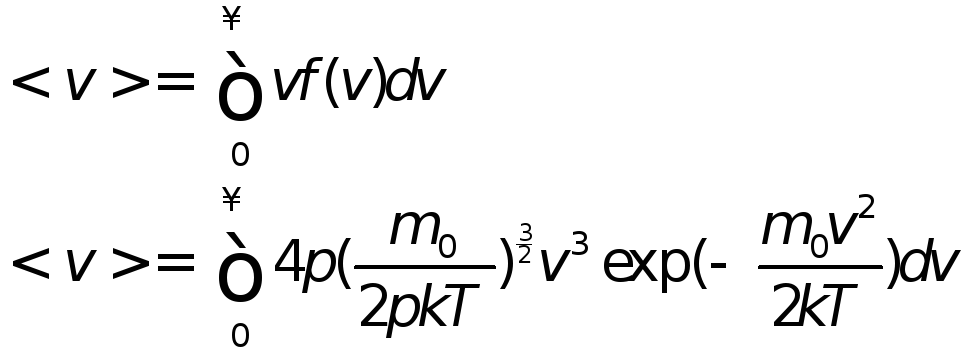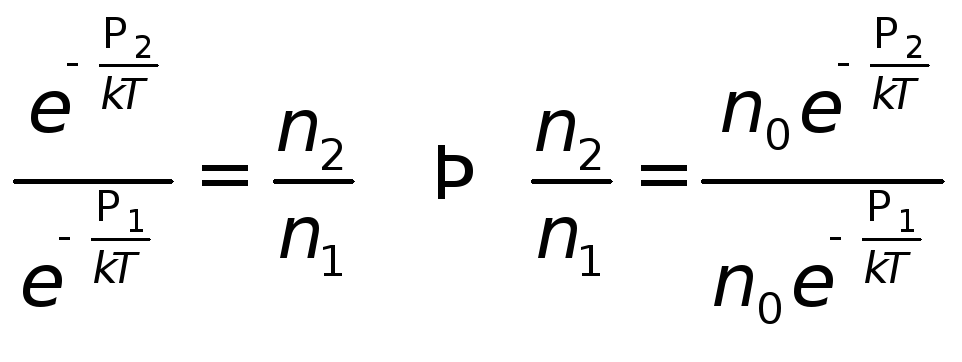Тип 14 № 1058
i
Определите среднюю квадратичную скорость броуновской частицы при температуре 27 °С. Броуновскую частицу рассматривайте как шарик радиусом 1,5 мкм, плотность которого равна 2700 кг/м3.
Спрятать решение
Решение.
Средняя квадратичная скорость равна Масса броуновской частицы
где ее объем равен
Объединив формулы, получаем:
Ответ: 0,57 мм/с.
Источник: Кирик Л. А. Самостоятельные и контрольные работы для 10 класса, Х.: «Гимназия», 2002 (№ 5 (высок.) стр. 11)
Наиболее
вероятная скорость.
Наиболее вероятная
скорость молекул идеального газа
соответсвует максимуму функции f(v).
Следовательно, эта скорость может быть
найдена из выражения
|
|
(13.18) |
Средняя
скорость молекул.
По определению:
|
|
Есть табличный
интеграл:
|
|
В нашем случае
Откуда получаем:
|
|
(13.19) |
средняя
квадратичная скорость <Vкв>
молекул.
|
|
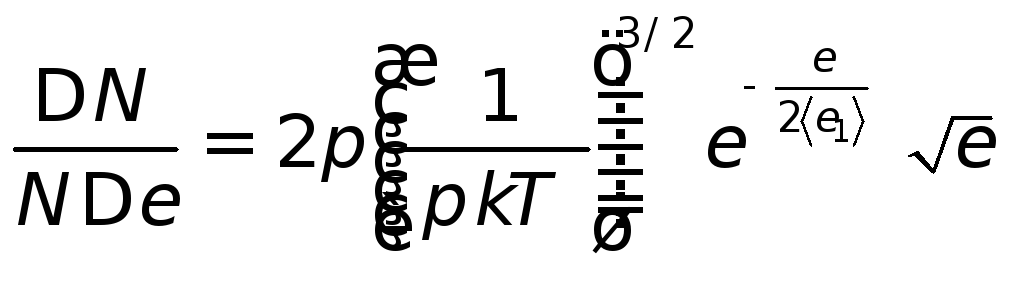
По определению
|
|
Есть табличный
интеграл:
|
|
В нашем случае
Получаем:
|
|
(13.20) |
Скорости,
характеризующие состояние газа.
|
Наиболее |
|
|
Средняя |
|
|
средняя |
|
Где:
k
– постоянная Больцмана;
m0
–
масса
молекулы;
Т – термодинамическая
температура;
R
– молярная газовая постоянная;
– молярная масса.
13. 2. 4. Распределение Максвелла в безразмерном виде.
Зачатую бывает
удобно провести анализ или решение
задачи воспользовавшись распределением
Максвелла по скоростям в безразмерном
виде. Что получить распределение в такой
записи перейдем к безразмерной скорости
|
|
Тогда выражение
(13.16) примет вид
|
|
(13.21) |
13. 2. 5. Распределение Максвелла по энергиям.
Преобразует
выражение (13.6) с помощью замен
(среднее значение энергии, приходящееся
на одну степень свободы) и(кинетическая энергия частицы). Тогда
и
|
|
или после перехода
к безразмерной величине
|
|
(13.22) |
Это
и есть распределение Максвелла по
энергиям
13. 3. Распределение Больцмана. Газ в силовом поле.
|
Перейдем к |
|
|
Рисунок 13.3. |
Пусть в первом
объеме молекулы газа обладают потенциальной
энергией
,
а во втором.
Согласно формулам (13.3) и (13.9) вероятности
того, что молекулы обладают такими
значениями потенциальной энергии (т.е.,
и.)
будут соответственно равны
|
|
(13.23) |
Здесь
– некоторый числовой множитель.
С другой стороны
эти вероятности
и
должны относиться друг к другу в той же
пропорции, что и количества частиц в
выбранных объемах при одинаковых в них
температурах
|
|
(13.24) |
Подставим в левую
часть этого равенства (13.23), а числитель
и знаменатель правой дроби поделим на
величину выбранного объема
.
Тогда учтя, что концентрация частиц,
после упрощений получаем
|
|
Отсюда следует,
что
|
|
(13.25) |
или
|
|
(13.26) |
где
– концентрация частиц в местоположении
частиц газа с нулевой потенциальной
энергией. Данное выражениеназывается
распределение Больцмана
(при постоянной температуре).
Анализ данного
выражения показывает, что силовое
поле принуждает собираться частицы
газа в местах с минимальной потенциальной
энергией, а тепловое движение приводит
к разбрасыванию частиц по пространству.
Соседние файлы в папке физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Kinetic Theory of Gases RMS Example
Blend Images / Eric Raptosh Photography / Getty Images
Updated on January 30, 2020
This example problem demonstrates how to calculate the root mean square (RMS) velocity of particles in an ideal gas. This value is the square root of the average velocity-squared of molecules in a gas. While the value is an approximation, especially for real gases, it offers useful information when studying kinetic theory.
Root Mean Square Velocity Problem
What is the average velocity or root mean square velocity of a molecule in a sample of oxygen at 0 degrees Celsius?
Solution
Gases consist of atoms or molecules that move at different speeds in random directions. The root mean square velocity (RMS velocity) is a way to find a single velocity value for the particles. The average velocity of gas particles is found using the root mean square velocity formula:
μrms = (3RT/M)½
μrms = root mean square velocity in m/sec
R = ideal gas constant = 8.3145 (kg·m2/sec2)/K·mol
T = absolute temperature in Kelvin
M = mass of a mole of the gas in kilograms.
Really, the RMS calculation gives you root mean square speed, not velocity. This is because velocity is a vector quantity that has magnitude and direction. The RMS calculation only gives the magnitude or speed. The temperature must be converted to Kelvin and the molar mass must be found in kg to complete this problem.
Step 1
Find the absolute temperature using the Celsius to Kelvin conversion formula:
- T = °C + 273
- T = 0 + 273
- T = 273 K
Step 2
Find molar mass in kg:
From the periodic table, the molar mass of oxygen = 16 g/mol.
Oxygen gas (O2) is comprised of two oxygen atoms bonded together. Therefore:
- molar mass of O2 = 2 x 16
- molar mass of O2 = 32 g/mol
- Convert this to kg/mol:
- molar mass of O2 = 32 g/mol x 1 kg/1000 g
- molar mass of O2 = 3.2 x 10-2 kg/mol
Step 3
Find μrms:
- μrms = (3RT/M)½
- μrms = [3(8.3145 (kg·m2/sec2)/K·mol)(273 K)/3.2 x 10-2 kg/mol]½
- μrms = (2.128 x 105 m2/sec2)½
- μrms = 461 m/sec
Answer
The average velocity or root mean square velocity of a molecule in a sample of oxygen at 0 degrees Celcius is 461 m/sec.
Средняя скорость молекул
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
υotn=28kTπm0=2υ.
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
υkυ=1N∑i=1Nυi2
Формулу средней квадратичной скорости можно переписать так:
υkυ2=∫0∞υ2Fυdυ.
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
υkυ=3kTm0=3RTμ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
p=13nm0υkυ,
где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
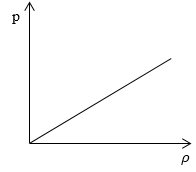
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).
Рисунок 1
Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
υ=8kTπm0
Из графика видно, что p~ρ или p=Cρ, где C – это некоторая константа.
m0=ρn, p=nkT=Cρ→kT=Cρn
Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:
υ=8kTπm0=8Cρπnnρ=8Cπ
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?
Решение
Применим выражение для υkυ:
υkυ=3RTμ
Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:
pV=mμRT=NNART.
Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:
p=nNART→RT=pNAn
Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:
υkυ=3pNAμn
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.
Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.
Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см3 при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.
Что такое средняя скорость движения молекул
Среднюю скорость движения молекул часто именуют скоростью их теплового движения.
Определение 1
Вид формулы средней относительной скорости молекул в физике можно представить выражением:
[text { Vотн }=sqrt{2} sqrt{frac{8 R T}{pi m_{0}}}]
Выражение под корнем – средняя скорость молекул идеального газа.
Как определить среднюю квадратичную скорость движения молекул
Определение 2
Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.
Средняя скорость молекул равна:
[leftlanglemathrm{V}_{mathrm{KB}}rightrangle=sqrt{frac{1}{N} sum_{i=1}^{N} v_{i}^{2}}]
Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:
[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]
Ещё одно выражение для среднеквадратичной скорости:
[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории
P = (1/3)nm*<Vкв>
Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.
Пример. 1.
Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:
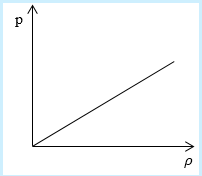
Напомним, что средняя скорость частиц:
[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]
Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ. Эти две величины можно связать соотношением
P=C*ρ
Где С – некоторая постоянная величина, константа.
Далее считаем m0= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.
Нужно лишь подставить эти значения в формулу для средней скорости:
[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]
В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.
Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.
Нет времени решать самому?
Наши эксперты помогут!
Пример. 2.
Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).
Воспользуемся формулой:
[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Также нам потребуется уравнение Менделеева-Клайперона
Здесь мы воспользовались тем, что:
m/μ = N/Na
PV = (m/μ)*RT = (N/Na)*RT
Если обе части этого уравнения поделить на V и принять во внимание, что
(N/V) = n, то можно получить
P = (n/Na)*RT. Отсюда находим, что RT = (p*N)/n
Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]
Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:
[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]