|
Что такое средневзвешенное значение и чем оно отличается от среднего значения? По какой формуле можно посчитать средневзвешенное значение? Средневзвешанное значение можно частенько встретить в статистике. Итак, разберемся, что же это такое. Это среднее арифметическое значение, которое еще учитывает вес каждого из слагаемых, для которых и рассчитывается это среднее значение. Задача: Куплены две партии апельсин , причем первая партия – 10 тонн и цена этой партии 700000, тонна стоит 70000, а вот вторая партия – 5 тонн по цене за партию 375000, тонна стоит 75000 ; если посчитать просто среднюю цену закупки , то получится (70000+75000) : 2 = 72500 за тонну. Средневзвешнная же цена более точно показывает нам цену товара с учетом объемов каждой партии равна (10 × 70000) + (5 × 75000) /(10+5) = 71666 за тонну. Думаю, теперь можно разобраться, что это такое за значение и как считать средневзвешенное значение в конкретном примере система выбрала этот ответ лучшим
Ксарфакс 4 года назад Средневзвешенное значение – это среднее значение с учётом веса (важности) каждого элемента из совокупности. Его можно посчитать по формуле: Средневзвешенное значение = (x1*w1 + x2*w2 + x3*w3 + … + xn*wn) / (w1 + w2+ … + wn). Здесь: x1, x2, x3, …, xn – это значения (например, цена или какая-то оценка). w1, w2, w3, …, wn – вес каждого значения. ** Пример. За день были проданы следующие товары: 1) Товар А – 10 штук по цене 1000 руб. 2) Товар B – 20 штук по цене 600 руб. 3) Товар C – 5 штук по цене 2000 руб. Средневзвешенную цену продажи можно найти следующим образом: (10 * 1000 + 20 * 600 + 2000 * 5) / (10 + 20 + 5) = 32000 / 35 = 914,29 руб. В программе Excel средневзвешенное значение можно найти с помощью функций СУММПРОИЗВ и СУММ.
Дублон 2 месяца назад Под средневзвешенном значением мы понимаем такое среднее значение, где учитывается вес (важность) каждого слагаемого и чаще всё это значимое применяется в статистике, экономике, физике. Допустим, нам надо узнать средневзвешенную скорость автомобиля, который проехал за несколько промежутков времени с разной скоростью. Автомобиль проехал за первые 20 минут со скоростью 30 километров в час, далее в течение 30 минут проехал со скорость. 40 километров в час, а затем с течение 10 минут промчался уже со скоростью 100 километров в час.
Подсчитываем: за первый промежуток времени автомобиль 20х30, за второй промежуток – 30х40, за третий промежуток – 10х100. Всё складываем и делим на сумму времени. 20х30+30х40+10х100 / 20+30+10 = 2800/60=46,6 километров в час Получается, что наш автомобиль ехал со средневзвешенной скоростью 46,6 километров в час.
Бутафога 2 месяца назад Считается, что средневзвешенное значение более точное по сравнению с обычным средним благодаря учитывания относительной важности данных. Этим значением часто пользуются инвесторы, приведем небольшой пример. Допустим, физическое лицо в первый год закупил 1000 акций по 10 рублей. В следующем году взял ещё 500 акций, но уже по 40 рублей. Делаем простой подсчет. В первый год: 1000 x 10 = 10000 рублей Во второй год: 500 x 40 = 20000 рублей Получается, что за два года за 1500 акций потрачено 10000 + 20000 = 30000 рублей. Делим общую сумму 30000 рублей на количество акций 1500, получится 20 рублей (средневзвешенное значение). SVFE48 4 месяца назад Средневзвешенное значение, также известное как средневзвешенное, представляет собой меру центральной тенденции, которая учитывает относительную важность каждого значения в наборе данных. Он рассчитывается путем умножения каждого значения в наборе данных на вес, который представляет его относительную важность, а затем суммирования этих взвешенных значений и деления на общий вес. Чтобы рассчитать средневзвешенное значение, вам необходимо выполнить следующие шаги: Присвойте вес каждому значению в наборе данных. Вес представляет относительную важность этого значения. Умножьте каждое значение в наборе данных на его вес. Суммируйте взвешенные значения. Добавьте общий вес. Разделите сумму взвешенных значений на общий вес, чтобы получить средневзвешенное значение. Средневзвешенное значение широко используется в различных областях, таких как финансы, статистика и контроль качества. Например, в финансах отношение цены акции к прибыли (P/E) представляет собой средневзвешенное значение, где знаменатель — количество акций в обращении, а числитель — рыночная капитализация. Krustall более года назад Средневзвешенное значение — это некое среднее значение, учитывающее вес или важность каждого элемента во всей совокупности. Средневзвешенное значение можно рассчитать по формуле: средневзвешенное значение=(x1*w1+x2*w2+x3*w3+…+xn*wn)/(w1+w2+…+wn). Здесь обозначения такие:x1, x2, x3, …, xn — значения (например, цена или какая-то оценка). w1, w2, w3, …,wn-вес каждого значения. В Excel вы можете найти средневзвешенное значение с помощью СУММ ПРОИЗВ и СУММ. Среднее или среднее арифметическое не учитывает вес каждого числа, а только сумму всех чисел, делённую на это число. Вес – это степень важность числа. Лара Изюминка 2 года назад Чтобы разобраться, что такое средневзвешанное значение стоит рассмотреть следующий пример. Итак, среденевзвешаннное значение – это среднее арифметическое значение, в котором учитывается вес каждого из слагаемых, для которых рассчитывается это среднее значение. Например, если кто-то покупает некий товар 2 партиями, одна из которых – 200 тонн по 500 тыс. рублей за тонну, другая – 300 тонн по 700 тыс руб за тонну, то тогда он закупает 500 тонн товара; обычная средняя цена закупки составит (500+700) : 2 = 600 тыс руб. Средневзвешнная цена учитывает объемы каждой из партий равна (200 × 500) + (300 × 700) /(200+300) = 620 тыс. руб за тонну. По примеру, становится понятно как считать средневзвешенное значение. Ну, а формулы приведены в ответах выше.
Nastya Chuk 3 года назад Добрый день! Актуальный вопрос на самом деле, поскольку я и сама недавно искала формулу в интернете. Итак, средневзвешенное значение – это есть среднее значение с учётом веса каждого элемента из некой совокупности. Как можно рассчитать? Все достаточно просто , вот формула: Среднзнач = (x1*w1 + x2*w2 + x3*w3 + … + xn*wn) деленное на (w1 + w2+ … + wn), где xn – это есть само значения , а wn – вес каждого значения.
smile6008 3 года назад Средневзвешенное значение – это значение, в котором учитывают не только среднее арифметическое, но и вес каждого числа. Для того чтобы рассчитать это значение, нужно воспользоваться формулой.
Среднее или среднеарифмитическое не учитывает вес каждого числа, а лишь составляет сумму всех чисел, делённое на количество. Вес – это степень важности числа. В экселе это значение можно рассчитать таким образом :
Средневзвешенное значение является средним значением при учете веса каждого элемента, согласно совокупности с возможным расчетом по формуле: Так, x1, x2, x3, …, xn является значением, так может быть отражена оценка, а также цена. Если говорить о w1, w2, w3, …, wn, то речь здесь идет о весе значения, относящегося к каждому. Знаете ответ? |
27 октября 2021 г.
Основные выводы:
-
Средневзвешенное значение — это среднее значение набора чисел, каждое из которых имеет разные связанные с ним «веса» или значения.
-
Чтобы найти средневзвешенное значение, умножьте каждое число на его вес, а затем сложите результаты.
-
Если веса не дают в сумме единицу, найдите сумму всех переменных, умноженных на их веса, а затем разделите на сумму весов.
Метод средневзвешенного значения — это инструмент, используемый, среди прочего, в аудиториях, отделах статистического анализа и бухгалтерского учета. Средневзвешенное значение помогает пользователю получить более точное представление о наборе данных, чем простое среднее значение. Точность чисел, которые вы получаете с помощью этого метода, определяется весом, который вы даете конкретным переменным в наборе данных.
В этой статье мы рассмотрим, как рассчитать средневзвешенное значение, используя два метода.
Что такое средневзвешенное значение?
Средневзвешенное значение — это среднее значение набора данных, в котором определенные числа признаются более важными, чем другие. Средневзвешенные значения обычно используются в статистическом анализе, портфелях акций и средних оценках учителей. Это важный инструмент для учета колебаний запасов, неравномерных или искаженных данных и обеспечения того, чтобы аналогичные точки данных были равными в представленной пропорции.
Пример средневзвешенного значения
Средневзвешенное значение — это одно из средств, с помощью которого бухгалтеры рассчитывают стоимость товаров. В некоторых отраслях, где количества смешаны или их слишком много для подсчета, полезен метод средневзвешенного значения. Это число входит в расчет себестоимости проданных товаров. Другие методы калькуляции включают в себя последний пришел, первый ушел и первый пришел, первый ушел или ЛИФО и ФИФО соответственно.
Пример:
Производитель покупает 20 000 единиц товара по 1 доллару за штуку, 15 000 единиц по 1,15 доллара за штуку и 5000 единиц по 2 доллара за штуку. Используя единицы в качестве веса и общее количество единиц в качестве суммы всех весов, мы приходим к следующему расчету:
1(20 000) + 1,15 (15 000) + 2 (5 000) / (20 000 + 15 000 + 5 000) = (20 000 + 17 250 + 10 000) / (20 000 + 15 000 + 5 000) = 47 250 / 40 180 =
Это соответствует средневзвешенной стоимости в размере 1,18 доллара за единицу.
Как рассчитать средневзвешенное значение
Средневзвешенное значение отличается от нахождения нормального среднего значения набора данных, потому что итог отражает то, что некоторые фрагменты данных имеют больший «вес» или большую значимость, чем другие, или встречаются чаще. Вы можете рассчитать средневзвешенное значение набора чисел, умножив каждое значение в наборе на его вес, а затем сложив произведения.
Чтобы получить более подробное объяснение приведенной выше формулы средневзвешенного значения, выполните следующие действия:
-
Определить вес каждой точки данных
-
Умножьте вес на каждое значение
-
Сложите результаты второго шага вместе
1. Определите вес каждой точки данных
Вы определяете вес точек данных, учитывая, какие числа являются наиболее важными. Учителя часто придают большее значение тестам и работам, чем, например, викторинам и домашним заданиям. В больших наборах статистических данных, таких как интеллектуальный анализ данных о поведении потребителей или перепись населения, рандомизированные деревья данных используются для определения важности переменной в наборе данных. Это помогает обеспечить беспристрастное распределение важности. Этот процесс обычно выполняется с помощью компьютерной программы. В бухгалтерских и финансовых целях количество единиц продукта используется в качестве весового коэффициента.
Пример:
-
Вы набираете 76 баллов за тест, что составляет 20% от вашей итоговой оценки. Процент вашей оценки — это вес, который она несет.
-
Инвестор покупает 50 акций по 100 долларов каждая. Купленные акции служат весом.
2. Умножьте вес на каждое значение
Как только вы узнаете вес каждого значения, умножьте вес на каждую точку данных.
Пример:
В наборе данных из четырех результатов тестов, где окончательный тест имеет больший вес, чем другие:
-
50(0,15) = 7,5
-
76(0,20) = 15,2
-
80(0,20) = 16
-
98(0,45) = 44,1
3. Сложите результаты второго шага вместе
Подсчитайте сумму всех взвешенных значений, чтобы получить средневзвешенное значение.
Пример:
7,5 + 15,2 + 16 + 44,1 = 82,8
Средневзвешенный показатель составляет 82,8%. Используя нормальное среднее, где мы вычисляем сумму и делим ее на количество переменных, средний балл будет 76%. Метод средневзвешенного значения подчеркивает важность выпускного экзамена по сравнению с другими.
Расчет средневзвешенного балла за тест Присвоенный вес Балл за тест Взвешенное значение 50,15 7,5 76,20 15,2 80,20 16 98,45 44,1 Средневзвешенное значение 82,8
Как рассчитать средневзвешенное значение, если веса не равны единице
Иногда вам может понадобиться рассчитать среднее значение набора данных, которое не дает в сумме 1 или 100 %. Это происходит при случайном сборе данных из популяций или событий в исследованиях. Вы можете рассчитать средневзвешенное значение этого набора чисел, умножив каждое значение в наборе на его вес, затем сложив продукты и разделив сумму продуктов на сумму всех весов.
Чтобы получить более подробное объяснение приведенной выше формулы средневзвешенного значения, если сумма весов не равна единице, выполните следующие действия:
-
Определить вес каждого числа
-
Найдите сумму всех весов
-
Вычислите сумму каждого числа, умноженного на его вес
-
Разделите результаты третьего шага на сумму всех весов.
1. Определить вес каждого числа
Чтобы определить вес каждого числа, учитывайте его важность для вас или частоту появления. Если вы пытаетесь рассчитать среднее количество бизнес-лидов, которые вы преследуете, вы можете захотеть, чтобы лиды, которые превращаются в продажи, имели больший вес, чем холодные звонки. Чтобы найти средневзвешенное значение без дополнительного смещения, вычислите частоту появления числа в качестве веса переменной. Это отражает его влияние на весь набор данных.
Пример. Подсчитайте среднее время, которое вы тратите на тренировки четыре дня в неделю в течение месяца или четырех недель. Время, которое вы потратили на тренировки в любой день, является набором данных. Количество дней, в течение которых вы тренировались в среднем, является весом, который вы будете использовать.
-
7 дней вы тренировались по 20 минут
-
3 дня вы тренировались по 45 минут
-
4 дня вы тренировались по 15 минут
-
2 дня ты должен был тренироваться и не сделал
2. Найдите сумму всех весов
Следующим шагом к нахождению средневзвешенного значения набора данных, не равного 1, является добавление суммы общего веса. Из нашего предыдущего примера у вас должно быть в общей сложности 16 дней, потраченных на тренировки:
3. Подсчитайте сумму каждого числа, умноженного на его вес.
Используя числа частоты, умножьте каждое на время, которое вы потратили на тренировки. Общая сумма дает вам сумму переменных, умноженных на их соответствующие веса.
Пример:
-
20(7) = 140
-
45(3) = 135
-
15(4) = 60
-
0(2) = 0
-
140 + 135 + 60 + 0 = 335
4. Разделите результаты третьего шага на сумму всех весов.
Формула для нахождения средневзвешенного значения представляет собой сумму всех переменных, умноженных на их веса, а затем деленную на сумму весов.
Пример:
Сумма переменных (вес) / сумма всех весов = средневзвешенное значение
335/16 = 20,9
Средневзвешенное время, которое вы потратили на тренировки за месяц, составляет 20,9 минут.
Download Article
Download Article
A weighted average, otherwise known as a weighted mean, is a little more complicated to figure out than a regular arithmetic mean. As the name suggests, a weighted average is one where the different numbers you’re working with have different values, or weights, relative to each other. For example, you may need to find a weighted average if you’re trying to calculate your grade in a class where different assignments are worth different percentages of your total grade. The procedure you use will be a little different depending on whether or not your total weights add up to 1 (or 100%).
-

1
Gather the numbers you would like to average. You’ll need to start by assembling a list of the numbers for which you’d like to find the weighted average. For example, if you’re trying to find a weighted average for a series of grades in a class, first write down each of the grades.[1]
- For instance, maybe your total grades are 82 for quizzes, 90 on your exam, and 76 on your term paper.
-

2
Determine the weight value of each number. Once you have your numbers, you’ll need to know how much each of them weighs, or is worth, as part of your final average. For instance, in your class, the quizzes might be worth 20% of your total grade, while the exam is 35% and the term paper is 45%. In this case, the weights add up to 1 (or 100%).[2]
- In order to use these percentages in your calculation, you’ll need to convert them to decimal form. The resulting numbers are called “weighting factors.”
Tip: Converting a percentage to a decimal is simple! Place a decimal point at the end of the percentage value, then move it over 2 places to the left. For example, 75% becomes 0.75.
Advertisement
-

3
Multiply each number by its weighting factor (w). Once you have all your numbers, pair up each number (x) with its corresponding weighting factor (w). You’ll be multiplying each set of numbers and weights together, then adding them all up to find the average.[3]
- For example, if your total quiz score is 82 and quizzes are worth 20% of your grade, multiply 82 x 0.2. In this case, x=82 and w=0.2.
-

4
Add the resulting numbers together to find the weighted average. The basic formula for a weighted average where the weights add up to 1 is x1(w1) + x2(w2) + x3(w3), and so on, where x is each number in your set and w is the corresponding weighting factor.[4]
To find your weighted average, simply multiply each number by its weight factor and then sum the resulting numbers up, the same way you would take the average of any other data set.[5]
For example:- The weighted average for your quiz grades, exam, and term paper would be as follows: 82(0.2) + 90(0.35) + 76(0.45) = 16.4 + 31.5 + 34.2 = 82.1. This means you have a grade of 82.1% in the course.
Advertisement
-

1
Write down the numbers you want to average. When you’re calculating a weighted average, the different weights will not always add up to 1 (or 100%). Either way, start by gathering your data, or the individual numbers for which you’d like to find your average.[6]
- For example, maybe you’re trying to figure out how many hours of sleep you get each night on average over the course of 15 weeks, but it varies from week to week. You may sleep 5, 8, 4, or 7 hours a night.
-

2
Find the weight of each number. Once you know your numbers, figure out the total weight associated with each number. For example, let’s say that on average, over the course of 15 weeks, there were some weeks when you slept more hours per night than others. The weeks that are most representative of how much you usually sleep would have more “weight” than the others. You would use the number of weeks associated with each amount of sleep as your weighting factor. For instance, putting the weeks in order by weight:[7]
- 9 weeks when you slept 7 hours a night on average.
- 3 weeks when you slept 5 hours a night.
- 2 weeks when you slept 8 hours a night.
- 1 week when you slept 4 hours a night.
- The number of weeks associated with each number of hours is your weighting factor. In this case, you slept 7 hours a night during most weeks, while there were relatively few weeks when you slept more or fewer hours.
-

3
Calculate the sum of all the weights. In order to determine the weighted average, you’ll need to figure out how much all the weights are worth when you put them together. To do this, simply add up all the weights. In the case of your sleep study, you already know that the total of all the weights is 15, since you are examining your sleep patterns over the course of 15 weeks.[8]
- The total number of weeks you looked at adds up as follows: 3 weeks + 2 weeks + 1 week + 9 weeks = 15 weeks.
-

4
Multiply the numbers by their weights and add up the results. Next, multiply each number in your data set by its corresponding weight, just as you would if the weights added up to 1 (or 100%). Add the resulting numbers together. For example, if you’re calculating the average amount of sleep you got each night over the series of 15 weeks, multiply the average number of hours you slept per night by the corresponding number of weeks. You would get:[9]
- 5 hours per night (3 weeks) + 8 hours per night (2 weeks) + 4 hours per night (1 week) + 7 hours per night (9 weeks) = 5(3) + 8(2) + 4(1) + 7(9) = 15 + 16 + 4 + 63 = 98
-

5
Divide the result by the sum of the weights to find the average. Once you’ve multiplied each number by its weighting factor and added the results, divide the resulting number by the sum of all the weights. This will tell you the weighted average. For example:[10]
- 98/15 = 6.53. This means you slept an average of 6.53 hours each night over the course of 15 weeks.
Advertisement
Practice Problems
Add New Question
-
Question
How do I find a weighted average?

Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Assistant Professor of Mathematics
Expert Answer
Support wikiHow by
unlocking this expert answer.If you have the numbers 3, 5, and 10, to take a normal average, it would be 3+5+10, divided by the total number of data points—in this case 3. For a weighted average, you’d multiply each number by its weight first. For instance, if the first number is twice as important, it would have a weight of 2, while the others would have a weight of 1. In that case, it would be (3×2)+(5×1)+(10×1). Then, divide that by 3.
-
Question
I scored a 50 and a 70 on 2 tests worth 50% each. I scored 100 on 2 homeworks worth 25% each, and 7 on a quiz worth 25%. What would be my grade average?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor
Staff Answer
Support wikiHow by
unlocking this staff-researched answer.In this case, your weights add up to 1.75, or 175%. To find your score, first add up the individual scores multiplied by their weights: 50(.5) + 70(.5) + 100(.25) + 100(.25) + 7(.25) = 111.75. Then, divide the result by the total weight: 111.75/1.75 = 63.86. This means your grade average in the class is 63.86, which you can round up to 64.
-
Question
What is the formula for the average of scores?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor
Staff Answer
Support wikiHow by
unlocking this staff-researched answer.That depends on whether the total weights of the scores add up to 100%. If so, then you would multiply each score (x) by its percentage of the total grade (w) and add them all up. So the formula would look like x1(w1) + x2(w2), etc. If it’s possible to achieve a total score that is greater or less than 100%, you’d have to divide the sum of all scores(weights) by the total possible weight.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Article SummaryX
To calculate weighted average, first find the weight of each number you’re working with. For example, let’s say you’re trying to find the weighted average of your grades in a class. You got 82 on quizzes, 90 on exams, and 76 on your term paper. If quizzes are 20% of your grade, exams are 35%, and the final paper is 45%, that means the weight of 82 is 20%, the weight of 90 is 35%, and the weight of 76 is 45%. Convert the weights into decimals by moving the decimal point 2 places to the left. Now you have 0.2, 0.35, and 0.45. These decimals are called weighting factors. The next step is to multiply each number by its weighting factor. In our example, you would multiply 82 by 0.2, 90 by 0.35, and 76 by 0.45 and get 16.4, 31.5, and 34.2. Finally, add all of these products together to find the weighted average. 16.4 + 31.5 + 34.2 equals 82.1. Therefore, the weighted average of your grades is 82.1%. To learn how to calculate a weighted average when the weights don’t add up to 1, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 3,209,228 times.
Reader Success Stories
-

“This article described exactly how to do exactly what I wanted to do while being very clear, simple, and to the…” more
Did this article help you?
Метод средневзвешенного значения – это инструмент, используемый в учебных аудиториях, статистическом анализе и бухгалтерии, а также в других областях. Взвешенное среднее помогает пользователю получить более точный взгляд на набор данных, чем обычное среднее. Точность чисел, полученных с помощью этого метода, определяется весом, который вы придаете конкретным переменным в наборе данных.
В этой статье мы рассмотрим, как рассчитать средневзвешенное значение двумя методами. Мы предлагаем
Ключевые выводы:
-
Средневзвешенное среднее – это среднее значение набора чисел, каждое из которых имеет различные веса или значения.
-
Чтобы найти средневзвешенное значение, умножьте каждое число на его вес, а затем сложите результаты.
-
Если весовые коэффициенты не равны единице, найдите сумму всех переменных, умноженную на их вес, а затем разделите на сумму весовых коэффициентов.
Что такое средневзвешенное значение?
Средневзвешенное среднее – это среднее значение набора данных, при котором определенные числа считаются более важными, чем другие. Средневзвешенные средние обычно используются в статистическом анализе, портфелях акций и средних оценках учителей. Это важный инструмент для учета колебаний запасов, неравномерных или искаженных данных, а также для обеспечения равенства представленных аналогичных точек данных в пропорции.
Пример средневзвешенного значения
Средневзвешенная стоимость – это один из способов, с помощью которого бухгалтеры рассчитывают стоимость товаров. В некоторых отраслях промышленности, где количество смешанное или слишком большое для подсчета, полезен метод средневзвешенной стоимости. Это число входит в расчет себестоимости проданных товаров. Другие методы калькуляции себестоимости включают метод последний вошел, первый вышел и первый вошел, первый вышел , или LIFO и FIFO соответственно.
Пример:
Производитель закупает 20 000 единиц товара по цене $1 за штуку, 15 000 единиц по цене $1.15 за штуку и 5 000 по 2 доллара за штуку. Используя единицы продукции в качестве веса, а общее количество единиц продукции как сумму всех весов, мы получаем следующий расчет:
$1(20,000) + $1.15 (15,000) + $2 (5,000) (20,000 + 15,000 + 5,000) = ($20,000 + $17,250 + $10,000) ($20,000 + 15,000 + 5,000) = $47,250 40,000 = $1.18
Это равняется средневзвешенной стоимости в $1.18 за единицу.
Как рассчитать средневзвешенное значение
Средневзвешенное среднее отличается от обычного среднего значения набора данных, поскольку общее отражает, что некоторые части данных имеют больший вес , или большую значимость, чем другие, или встречаются чаще. Вы можете рассчитать средневзвешенное значение набора чисел, умножив каждое значение в наборе на его вес, а затем сложив полученные продукты.
Для более подробного объяснения приведенной выше формулы средневзвешенного значения выполните следующие шаги:
1. Определите вес каждой точки данных
Вы определяете вес точек данных, учитывая, какие цифры являются наиболее важными. Например, преподаватели часто оценивают тесты и работы более весомо, чем контрольные работы и домашние задания. В больших статистических наборах данных, таких как поиск данных о потребительском поведении или перепись населения, для определения важности переменной в наборе данных используются рандомизированные деревья данных. Это помогает обеспечить несмещенное распределение важности. Этот процесс обычно выполняется с помощью компьютерной программы. Для бухгалтерских и финансовых целей в качестве весового коэффициента используется количество единиц продукта.
Пример:
-
Вы набрали 76 баллов на тесте, который составляет 20% от вашей итоговой оценки. Процент от вашей оценки – это вес, который она имеет.
-
Инвестор приобретает 50 акций по 100 долларов каждая. В качестве веса выступают купленные акции.
2. Умножьте вес на каждое значение
Как только вы узнаете вес каждого значения, умножьте вес на каждую точку данных.
Пример:
В наборе данных из четырех тестов, где последний тест имеет больший вес, чем остальные:
-
50(.15) = 7.5
-
76(.20) = 15.2
-
80(.20) = 16
-
98(.45) = 44.1
3. Сложите результаты второго шага вместе
Рассчитайте сумму всех взвешенных значений, чтобы получить средневзвешенное значение.
Пример:
7.5 + 15.2 + 16 + 44.1 = 82.8
Средневзвешенное значение равно 82.8%. Используя обычное среднее, когда мы вычисляем сумму и делим ее на количество переменных, средний балл будет равен 76%. Метод средневзвешенного значения подчеркивает важность выпускного экзамена по сравнению с другими.
Расчет средневзвешенного значения
| Результат теста | Присвоенный вес | Тестовый балл Взвешенное значение |
| 50 | .15 | 7.5 |
| 76 | .20 | 15.2 |
| 80 | .20 | 16 |
| 98 | .45 | 44.1 |
| Средневзвешенное значение | 82.8 |
Как рассчитать средневзвешенное значение, если весовые коэффициенты не равны единице
Иногда вам может понадобиться рассчитать среднее значение набора данных, которое не может быть равно 1 или 100%. Это происходит при случайном сборе данных из популяций или случаев в исследовании. Вы можете рассчитать средневзвешенное значение этого набора чисел, умножив каждое значение в наборе на его вес, затем сложив продукты и разделив сумму продуктов на сумму всех весов.
Для более подробного объяснения приведенной выше формулы средневзвешенного, когда веса не складываются в единицу, выполните следующие действия:
1. Определите вес каждого числа
Чтобы определить вес каждого числа, подумайте о его важности для вас или частоте появления. Если вы пытаетесь рассчитать среднее количество деловых предложений, которые вы получаете, вы можете предположить, что предложения, которые превращаются в продажи, будут иметь больший вес, чем холодные звонки. Чтобы найти средневзвешенное значение без дополнительного смещения, рассчитайте частоту встречаемости числа как вес переменной. Это отражает его влияние на весь набор данных.
Пример: Рассчитайте среднее время, которое вы тратите на физические упражнения четыре дня в неделю в течение месяца или четырех недель. Время, которое вы потратили на физические упражнения в любой конкретный день, является набором данных. Количество дней, в течение которых вы занимались спортом в среднем, – это вес, который вы будете использовать.
-
7 дней вы занимались спортом в течение 20 минут
-
3 дня вы занимались спортом в течение 45 минут
-
4 дня вы занимались спортом в течение 15 минут
-
2 дня, когда вы должны были заниматься спортом, но не делали этого
2. Найдите сумму всех весов
Следующим шагом для нахождения средневзвешенного значения набора данных, не равного 1, является сложение суммы общего веса. Из нашего предыдущего примера следует, что в общей сложности вы потратили на физические упражнения 16 дней:
-
7+3+4+2 = 16
3. Рассчитайте сумму каждого числа, умноженную на его вес
Используя числа частот, умножьте каждое из них на время, в течение которого вы занимались спортом. Общий итог дает сумму переменных, умноженную на их соответствующие веса.
Пример:
-
20(7) = 140
-
45(3) = 135
-
15(4) = 60
-
0(2) = 0
-
140 + 135 + 60 + 0 = 335
4. Разделите результаты третьего шага на сумму всех весов
Формула для нахождения средневзвешенного показателя – это сумма всех переменных, умноженная на их вес, затем деленная на сумму весов.
Пример:
Сумма переменных (вес) сумма всех весов = средневзвешенное значение
33516 = 20.9
Средневзвешенное значение времени, которое вы потратили на тренировки в течение месяца, равно 20.9 минут.
Skip to content
В этом руководстве демонстрируются два простых способа вычисления средневзвешенного значения в Excel – с помощью функции СУММ (SUM) или СУММПРОИЗВ (SUMPRODUCT в английском варианте).
В одной из предыдущих статей мы обсудили три основные функции для вычисления среднего в Excel, которые очень просты и просты в использовании.
Но что, если некоторые значения более важны, чем другие, и, следовательно, вносят больший вклад в конечное среднее значение? Например, если вы участвуете в экзаменах и все экзамены имеют одинаковый вес, они одинаково важны, то для вас важно именно среднее значение оценки.
Однако в реальной жизни это не всегда так. Например, если вы изучаете программирование, то насколько важны для вас оценки по истории и физкультуре по сравнению с оценками по профильным дисциплинам?
Некоторые задачи всегда важнее других. Некоторые экзамены важнее других.
В таких ситуациях вам как раз и необходимо рассчитывать средневзвешенное значение.
- Что такое средневзвешенное значение?
- Формулы для средневзвешенного значения в Excel
- Пример 1. Функция СУММ.
- Пример 2. Функция СУММПРОИЗВ
- Пример 3. Средневзвешенная цена.
Хотя Microsoft Excel не предоставляет специальной функции взвешенного среднего, он предоставляет несколько других, которые окажутся полезными в ваших вычислениях, что показано в следующих примерах.
Что такое средневзвешенное значение?
Оно является своего рода средним арифметическим, в котором некоторые элементы набора данных имеют большую значимость, чем другие. Другими словами, каждому исходному показателю присваивается определенный вес.
Оценки учащихся часто рассчитываются с использованием этого подхода, что видно на следующем скриншоте. Обычное среднее значение легко вычисляется с помощью СРЗНАЧ . Однако мы хотим, чтобы итог учитывал значимость каждого вида занятий, указанного в столбце C.
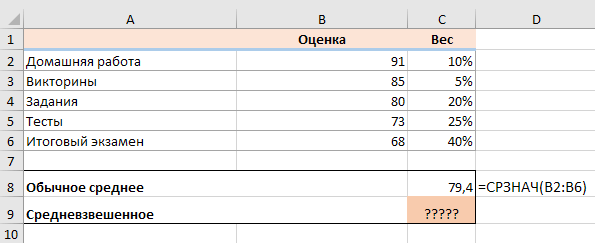
В математике и статистике вы вычисляете взвешенное среднее значение, умножая каждое число в наборе на его вес, затем складываете произведения и делите итог сложения произведений на сумму всех весомостей.
В этом примере, чтобы посчитать средневзвешенную итоговую оценку, вы умножаете каждый полученный балл на соответствующий процент (преобразованный в десятичную дробь), складываете эти 5 произведений вместе и делите это число на итог сложения пяти весов:
((91 * 0,1) + (85 * 0,05) + (80 * 0,2) + (73 * 0,25) + (68 * 0,4)) / (0,1 + 0,05 + 0,2 + 0,25 + 0,4) = 74,8
Обычная средняя оценка (79,4) и средневзвешенная (74,8) – это разные величины.
Формулы для средневзвешенного значения в Excel
В Microsoft Excel взвешенное среднее рассчитывается с использованием того же подхода, но с гораздо меньшими усилиями, поскольку функции Excel выполнят большую часть работы за вас.
Пример 1. Функция СУММ.
Если у вас есть базовые знания о ней , приведенная ниже формула вряд ли потребует какого-либо объяснения:
=СУММ(B2*C2; B3*C3; B4*C4; B5*C5; B6*C6)/СУММ(C2:C6)
По сути, он выполняет те же вычисления, что и описанные выше, за исключением того, что вы предоставляете ссылки на ячейки вместо чисел.
Посмотрите на рисунок чуть ниже: формула возвращает точно такой же результат, что и вычисления, которые мы делали минуту назад. Обратите внимание на разницу между нормальным средним, возвращаемым при помощи СРЗНАЧ в C8, и средневзвешенным (C9).
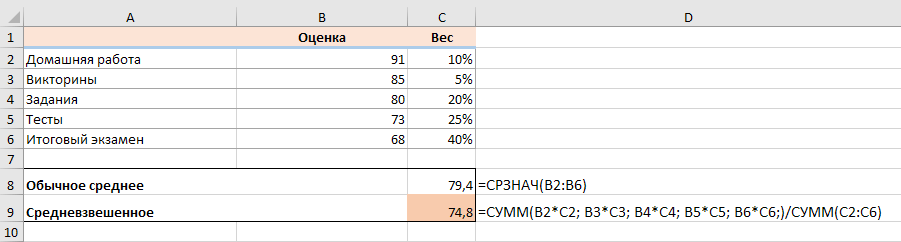
Несмотря на то, что формула эта очень проста и понятна, но она не подходит, если вы хотите усреднить большое количество элементов. Ведь придётся перечислять множество аргументов, что довольно утомительно.
В этом случае вам лучше использовать функцию СУММПРОИЗВ (SUMPRODUCT в английской версии). Об этом – ниже.
Пример 2. Функция СУММПРОИЗВ
Она идеально подходит для нашей задачи, так как предназначена для сложения произведений чисел. А это именно то, что нам нужно.
Таким образом, вместо умножения каждого числа на показатель его значимости по отдельности, вы предоставляете два массива в формуле СУММПРОИЗВ (в этом контексте массив представляет собой непрерывный диапазон ячеек), а затем делите результат на итог сложения весов:
= СУММПРОИЗВ(диапазон_значений ; диапазон_весов ) / СУММ( диапазон_весов )
Предполагая, что величины для усреднения находятся в ячейках B2: B6, а показатели значимости – в ячейках C2: C6, наша формула будет такой:
=СУММПРОИЗВ(B2:B6; C2:C6) / СУММ(C2:C6)

Итак, формула умножает 1- е число в массиве 1 на 1- е в массиве 2 (в данном примере 91 * 0,1), а затем перемножает 2- е число в массиве 1 на 2- е в массиве 2 (85 * 0,15). в этом примере) и так далее. Когда все умножения выполнены, Эксель складывает произведения. Затем делим полученное на итог весов.

Чтобы убедиться, что функция СУММПРОИЗВ дает правильный результат, сравните ее с формулой СУММ из предыдущего примера, и вы увидите, что числа идентичны.
В нашем случае сложение весов дает 100%. То есть, это просто процент от итога. В таком случае верный результат может быть получен также следующими способами:
=СУММ(B2*C2; B3*C3; B4*C4; B5*C5; B6*C6)
{=СУММ(B2:B6*C2:C6)}
Это формула массива, не забудьте, что вводить ее нужно при помощи комбинации клавиш CTRL+SHIFT+ENTER.
=СУММПРОИЗВ(B2:B6;C2:C6)
Но при использовании функции СУММ или СУММПРОИЗВ веса совершенно не обязательно должны составлять 100%. Однако, они также не должны быть обязательно выражены в процентах.
Например, вы можете составить шкалу приоритета / важности и назначить определенное количество баллов для каждого элемента, что и показано на следующем рисунке:

Видите, в этом случае мы обошлись без процентов.
Пример 3. Средневзвешенная цена.
Еще одна достаточно часто встречающаяся проблема – как рассчитать средневзвешенную цену товара. Предположим, мы получили 5 партий товара от различных поставщиков. Мы будем продавать его по одной единой цене. Но чтобы ее определить, нужно знать среднюю цену закупки. В тот здесь нам и пригодится расчет средневзвешенной цены. Взгляните на этот простой пример. Думаю, вам все понятно.
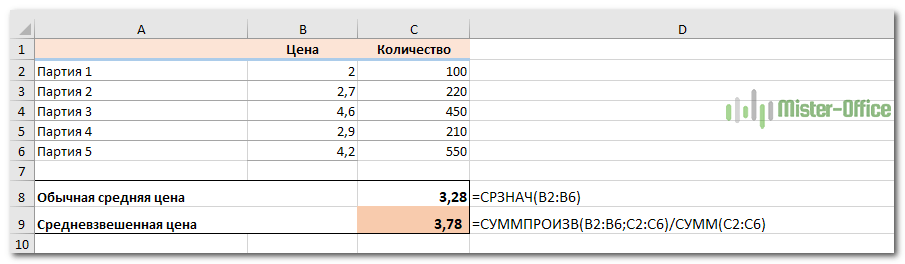
Итак, средневзвешенная цена значительно отличается от обычной средней. На это повлияли 2 больших партии товара по высокой цене. А формулу применяем такую же, как и при расчете любого взвешенного среднего. Перемножаем цену на количество, складываем эти произведения, а затем делим на общее количество товара.
Ну, это все о формуле средневзвешенного значения в Excel.
Рекомендуем также:





