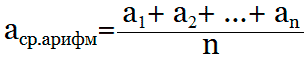Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Понятие среднее арифметическое ряда чисел можно встретить в разных сферах — в математике, статистике, инженерных расчетах и многих других.
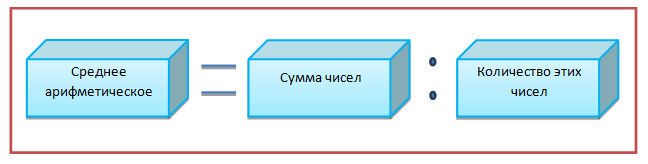
Чтобы найти среднее арифметическое чисел надо их сложить и эту сумму разделить на количество чисел.
Мы создали этот калькулятор для упрощения расчетов. Он с легкостью найдет среднее арифметическое 3, 4, 5 и даже 15 чисел. Следует упомянуть, что кроме среднего арифметического есть очень схожие понятия медианы и среднего гармонического.
Калькулятор среднего арифметического
Как найти среднее арифметическое
Допустим, что нам надо найти среднее арифметическое чисел 7 23 9 73 3. Сложим их и получим 7 + 23 + 9 + 73 + 3 = 115. Поделим эту сумму на количество чисел, то есть на 5:
222 / 5 = 23
Значит среднее арифметическое приведенных чисел равно 23.
Ваша оценка
[Оценок: 895 Средняя: 3.5]
Среднее арифметическое чисел Автор admin средний рейтинг 3.5/5 – 895 рейтинги пользователей
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.
Как найти среднее арифметическое
Это пригодится не только для решения школьных задачек, но и при различных подсчётах в обычной жизни.
Что такое среднее арифметическое
Среднее арифметическое — это сумма всех чисел в ряду, разделённая на количество слагаемых.
Как найти среднее арифметическое
Например, перед вами ряд чисел «1, 2, 3, 4, 5, 6». Как следует из определения, чтобы узнать среднее арифметическое, нужно сложить все данные вам числа, а потом разделить получившийся результат на количество этих чисел. В приведённом примере — на шесть. Вот как это выражается формулой:
Допустим, вам нужно определить среднее арифметическое для чисел 4, 5 и 6. Складываем 4 + 5 + 6 = 15. Теперь делим 15 на 3 и получаем 5. Это и будет среднее арифметическое.
Таким же образом оно подсчитывается для десятичных и обыкновенных дробей.
Пример расчёта среднего арифметического для обыкновенных дробей будет выглядеть так:
А это пример, как найти среднее арифметическое для десятичных дробей:
Как это пригодится в жизни
Среднее арифметическое помогает описать множество цифровых значений всего одним числом. Например, по выше представленной формуле можно подсчитать усреднённую цену на товар или среднюю зарплату сотрудников в одной организации, среднюю посещаемость заведения. Это полезно для ведения статистики и в случаях, когда нужно сжато изложить информацию.
Читайте также 🧐
- 7 причин полюбить математику
- 7 способов найти площадь прямоугольника
- 6 способов посчитать проценты от суммы с калькулятором и без
- Как освоить устный счёт школьникам и взрослым
- 10 увлекательных задач от советского математика
План урока:
Понятие среднего арифметического
Алгоритм нахождения среднего арифметического
Интересные факты
Понятие среднего арифметического
К сестрам Марине, Наталье, Елене в гости приехала бабушка. Она привезла своим внучкам гостинцы: восемнадцать конфет, шесть шоколадок, шесть киндер-сюрпризов. Сказала угощение разделить поровну. Определите, сколько сладостей достанется каждой девочке?
Ответ на вопрос, можно получить двумя способами. Рассмотрим их.
1
Чтобы выяснить, сколько сладостей достанется одной девочке, нужно каждый вид угощения разделить поровну – на 3.
Разделим конфеты между детьми:
18 : 3 = 6.
Теперь известно, что каждому ребенку досталось 6 конфет.
Разделим шоколадки:
6 :3 = 2.
Каждой внучке досталось две шоколадки.
Разделим шоколадные яйца:
6 : 3 = 2.
Выяснили, бабушка привезла по два киндер-сюрприза.
Стало известно, сколько гостинцев получил один ребенок. Теперь, вычислим, сколько сладостей досталось каждой девочке. Сложим количество конфет(6), шоколадок(2), киндер-сюрпризов(2), имеющихся у одной девочки:
6+2+2=10.
Получается, бабушка привезла по 10 сладостей.
Запишем решение задачи.
Как видите, способ, довольно простой, ноимеет длинную запись, занимает много времени. Рассмотрим второй способ решения задач такого вида.
2
Известно, сколько гостинцев привезла бабушка: конфет–восемнадцать, шоколадок – шесть, киндер-сюрпризов – шесть. Чтобы узнать количество гостинцев, доставшееся каждой сестре, сложим гостинцы и разделим поровну. То есть, суммируем привезенные подарки, делим на 3. Такой способ решения, имеет название в математике – «Нахождение среднего арифметического». Сформулируем, определение, среднего арифметического:
Среднее арифметическое нескольких чисел – результат деления суммы этих чисел на их количество
Используя, рассмотренное определение, найдем общее количество угощения, для этого сложим количество сладостей каждого вида конфеты + шоколадки + киндеры:
18+6+6=30.
Получается, что всего было 30 угощений. Теперь, эту сумму(30) делим на количество слагаемых(3), использованных в сумме:
30 : 3 =10.
Каждой внучке досталось по 10 сладостей.
Запишем решение этой задачи с использованием второго способа.
Как видите, второй способ, более краткий и удобный. Главное – запомнить изученное определение. Ведь, решение задач такого вида часто встречается на протяжении всего учебного процесса!
Алгоритм нахождения среднего арифметического
Рассмотрим следующую задачу.
Два брата-садовода продавали собранные фрукты. Первый брат продал яблок на 25000 рублей, а второй брат продал груш на сумму 15000 рублей. Все заработанные деньги братья разделили поровну. Сколько денег заработал каждый садовод?
Чтобы ответить на вопрос, необходимо использовать изученное правило.
Чтобы найти среднее арифметическое нескольких чисел, нужно сумму этих чисел разделить на их количество. Для этого:
1. Определяем количество слагаемых;
2. Находим сумму всех слагаемых;
3. Делим полученную сумму на количество слагаемых
В начале давайте определим количество слагаемых. Так как фрукты продавали два садовода, то и делить выручку будем между ними. То есть количество слагаемых в сумме – два.
Теперь можем найти общую сумму, заработанную братьями. Для этого, складываем выручку первого и второго брата:
25000+15000=40000
Всего они заработали 40000 рублей.
Зная, что общая сумма равна 40000 рублей, мы можем найти сумму заработка каждого садовода. Для этого полученную сумму (40000) делим на количество слагаемых (2):
40000 : 2 = 20000.
Получается, заработок садовода составил 20000 рублей.
В ходе решения данной задачи мы составили алгоритм нахождения среднего арифметического.
Запомни!
Алгоритм вычисления среднего арифметического:
1. Находим слагаемые и считаем их количество;
2. Суммируем все слагаемые;
3. Полученную сумму делим на количество слагаемых
Держи табличку всегда под рукой, тогда сможешь найти среднее арифметическое любых чисел!
Выполним задание.
Найди среднее арифметическое чисел 10,20,30,40.
Чтобы выполнить необходимые вычисления, вспоминаем,
среднее арифметическое – частное суммы всех слагаемых и их количества
Мы уже знаем, что для вычисления заданий, такого вида, существует специальный алгоритм. Используя данный алгоритм,выполним все необходимые действия.
Следуя определенному алгоритму, мы без труда выполнили задание.
Запомни формулу среднего арифметического!
В заключение нашего урока рассмотрим еще одну задачу.
В школе четыре пятых класса 5А,5Б,5В,5Г. 5А – 22 ученика, 5Б –30 учеников, 5В – 28 детей, 5Г – 20. Найдите, сколько детей училось бы в каждом классе, если во всех классах учеников будет поровну.
Исходя из условия, в этой задаче нужно найти среднее количество учеников в одном классе. Чтобы ответить на главный вопрос, необходимо воспользоваться алгоритмом вычисления среднего арифметического.
Значит, если бы во всех пятых классах школы, училось равное количество учеников, в каждом классе было по 25 детей.
Запишем решение.
Сегодня вы узнали, как найти среднее арифметическое число. Внимательно рассмотрите урок, и запомните основные определения и алгоритмы! Тогда, любая контрольная будет по плечу!
Интересные факты
- По статистике, дети улыбаются 400 раз в день, а взрослые всего 17. Улыбайтесь чаще!
- В России продолжительность жизни мужчин составляет 70 лет, женщин – 78 лет!
- Ежедневно в Росси рождается 5000 детей.
- Ученые подсчитали, за всю жизнь, человек тратит 5 лет на процесс приема пищи,
- Ученые подсчитали, за 70 лет, человек поглощает более 50000 килограммов пищи, в том числе около 200-300 килограммов поваренной соли. Так же, каждый человек, достигший 70 летнего возраста, выпил за всю жизнь 50000 литров воды, что больше в 1400 раз массы человеческого тела.
- Одной хорошей шариковой ручкой можно написать 50000 слов.
Когда трескается стекло, трещина распространяется со скоростью 5000 км/ч.