Средний диаметр
Cтраница 1
Средние диаметры dm и Dm определяют расчетом как среднее арифметическое наибольшего и наименьшего диаметров, измеренных в двух крайних сечениях кольца.
[1]
Средний диаметр d2 ( D2) – это диаметр воображаемого цилиндра, соосного с резьбой, образующие которого в любой осевой плоскости делятся боковыми сторонами витков на равные части. Этому определению соответствует измерение среднего диаметра методом трех проволочек.
[2]
Средний диаметр dcp – расстояние между двумя линиями, параллельными оси болта, из которых каждая находится на равном расстоянии от вершины нитки и дна впадины.
[3]
Средние диаметры, определенные по формулам (1.28) – (1.35), могут существенно различаться.
[5]
Средний диаметр d2 определяется в зависимости от степени точности резьбы.
[6]
Средний диаметр d эквивалентной плоской круговой катушки находят по диаметру D окружности, описанной вокруг среднего витка катушки, так же, как в случае соленоидов. При этом, пользуясь табл. 9 – 6, за аргумент принимают отношение г JD, где г – радиальный размер ( ширина обмотки) катушки.
[7]
Средний диаметр da – это диаметр воображаемого цилиндра, который делит профиль резьбы так, что ширина витка резьбы равна ширине соответствующего промежутка между витками. Средний диаметр измеряется в плоскости, перпендикулярной к оси болта или гайки.
[9]
Средний диаметр и число пружин берется из конструктивных соображений.
[10]
Средний диаметр является основным параметром, определяющим точность и характер сопряжения резьбовой пары, так как он определяет взаимное положение образующих профиля резьбы болта и гайки, по которым происходит сопряжение.
[11]
Средний диаметр измеряется при помощи резьбового микрометра и вставок с укороченным профилем и на соответствующих приборах в сочетании с проволочками по методу трех проволочек.
[12]
Средний диаметр равен 770 / 200 3 85 мкм. Из таблицы видно, что медианный диаметр лежит между значениями 2 и 3 мкм. По приведенным данным более точная оценка этой величины невозможна.
[13]
Средний диаметр d2 задается в плоскости Р на средней длине резьбы ( фиг.
[14]
Средний диаметр из-за усадки уменьшается и тем самым как бы вводится диаметральная компенсация. Это приводит к тому, что для длины свинчивания / – 0 577d диаметральная компенсация погрешности шага может приниматься пропорционально минимальной усадке. Однако, учитывая неравномерность усадки по диаметру и шагу, ее следует взять равной средней усадке.
[15]
Страницы:
1
2
3
4
5
Калькулятор объема цилиндра
Рассчитайте онлайн объем любого цилиндрического объекта: трубы, бочки, банки.
Что известно
Размерность
Радиус основания
см
Диаметр основания
см
Площадь основания
см2
Высота
см
Раcсчитать
🛢️ Когда требуется знать объем цилиндра?
Знание объема цилиндра может потребоваться в различных ситуациях, к примеру:
- Расчет объема бака или резервуара: если вы планируете хранить жидкость или газ в баке или резервуаре, то может быть важно знать его объем, чтобы знать, сколько материала вы можете в него поместить.
- Расчет объема емкости для транспортировки: если вы занимаетесь перевозкой жидкостей или газов, то может потребоваться знать объем емкости, чтобы убедиться, что вы можете перевезти нужное количество материала.
- Расчет объема цилиндрических труб: если вы занимаетесь установкой трубопроводов или работой с другими цилиндрическими объектами, то может быть полезно знать их объем, чтобы правильно рассчитать количество материала, необходимого для работы.
- Расчет объема бутылки или бочки: если вы хотите знать, сколько жидкости вы можете вместить в определенную бутылку или бочку, то калькулятор объема цилиндра может помочь рассчитать объем емкости.
- Определение объема цилиндрических объектов, используемых в декоративных целях, например, колонн, скульптур и других элементов архитектуры и дизайна.
Также умение рассчитывать объем цилиндра пригодится в строительстве, химии и фармацевтике, механике и технике, производстве, учебе и творчестве.
📏 Как рассчитывается объем цилиндра?
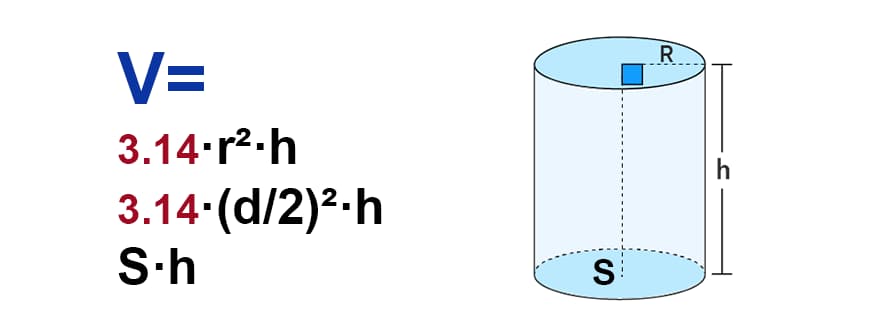
Объем цилиндра можно рассчитать по формуле:
V = πr²h
где V – объем цилиндра, r – радиус основания цилиндра, h – высота цилиндра, π (пи) – математическая константа, приблизительно равная 3,14.
Чтобы использовать эту формулу, необходимо знать значения радиуса основания и высоты цилиндра. Радиус основания – это расстояние от центра основания до края, высота цилиндра – это расстояние между основаниями цилиндра.
Например, если радиус основания цилиндра равен 5 см, а высота цилиндра составляет 10 см, то объем цилиндра можно рассчитать следующим образом:
V = 3,14 x 5² x 10 = 785 см3
Обратите внимание, что единицы измерения должны быть одинаковыми, чтобы получить правильный ответ. Если радиус основания и высота цилиндра измеряются в сантиметрах, то и объем цилиндра должен быть выражен в кубических сантиметрах.
🧮 Что такое калькулятор объема цилиндра?
Калькулятор объема цилиндра – это инструмент, который позволяет автоматически рассчитывать объем цилиндра по его размерам. Обычно калькулятор объема цилиндра предоставляет пользователю простую форму, где нужно ввести значение радиуса основания и высоты цилиндра, а затем нажать кнопку «Рассчитать». Калькулятор объема цилиндра может быть представлен в виде программы на компьютере или мобильном устройстве, а также в виде онлайн-сервиса на веб-сайте, как у нас.
Использование калькулятора объема цилиндра упрощает и ускоряет процесс расчета объема цилиндра, особенно если нужно рассчитать объем нескольких цилиндров или если значения радиуса и высоты цилиндра имеют сложные числовые значения. Калькулятор объема цилиндра может быть полезен в различных областях, включая науку, технику, строительство, производство, учебу и домашнее хозяйство.
📏 Как работает калькулятор объема цилиндра?
Калькулятор объема цилиндра работает на основе математической формулы для расчета объема цилиндра, рассмотренной выше.
Чтобы рассчитать объем цилиндра, пользователь должен ввести значения радиуса основания и высоты цилиндра в соответствующие поля калькулятора и нажать кнопку «Рассчитать». Калькулятор использует введенные значения, выполняет математическую операцию по формуле и выводит результат в соответствующем поле на экране.
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения (например, сантиметры или дюймы) и возможность рассчитать объем цилиндра, используя диаметр основания вместо радиуса.
🛢 Как использовать калькулятор объема цилиндра?
Для использования калькулятора объема цилиндра следуйте этим простым шагам:
- Откройте калькулятор объема цилиндра, который находится на компьютере, мобильном устройстве или на веб-сайте.
- Введите значение радиуса основания цилиндра в соответствующее поле калькулятора. Если вы используете калькулятор, который принимает во внимание диаметр, убедитесь, что вы выбрали правильную единицу измерения.
- Введите значение высоты цилиндра в соответствующее поле калькулятора. Убедитесь, что вы выбрали правильную единицу измерения.
- Нажмите кнопку «Рассчитать» или «Получить результат». Калькулятор выполнит расчеты и выведет объем цилиндра в соответствующем поле.
- Проверьте результаты и убедитесь, что все значения введены правильно и выбраны правильные единицы измерения.
- Если нужно рассчитать объем нескольких цилиндров, повторите шаги 2-5 для каждого цилиндра.
- Сохраните результаты или скопируйте их в буфер обмена, если нужно использовать их в другой программе или приложении.
В зависимости от функционала калькулятор может иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
В чем измеряется объем цилиндра?
Объем цилиндра измеряется в кубических единицах длины. Например, если размеры цилиндра измеряются в метрах, то его объем будет выражаться в кубических метрах (м³). Если размеры измеряются в сантиметрах, то объем будет выражаться в кубических сантиметрах (см³). Также можно использовать другие единицы измерения, такие как литры или галлоны, которые также выражают объем жидкости или газа, но они не являются кубическими единицами длины.
Несколько лайфхаков
Если вы хотите упростить расчет объема цилиндра, есть несколько лайфхаков, которые могут пригодиться:
- Используйте формулу площади основания цилиндра. Объем цилиндра можно вычислить, умножив площадь основания на высоту. Если вы знаете формулу площади основания цилиндра, то можете сначала вычислить ее, а затем умножить на высоту, чтобы найти объем.
- Используйте приближенное значение числа Пи. Число Пи является бесконечной десятичной дробью, но для большинства расчетов достаточно использовать его приближенное значение. Например, можно использовать значение 3,14 или 22/7 вместо точного значения числа Пи, которое равно примерно 3,14159265359.
- Используйте онлайн калькулятор. Наш онлайн калькулятор объема цилиндра поможет быстро выполнить расчеты за вас. Просто введите значения радиуса и высоты, и калькулятор автоматически вычислит объем.
- Используйте замены единиц измерения. Если вы хотите перевести объем из одной единицы измерения в другую, например, из кубических сантиметров в литры, можете также воспользоваться калькулятором на нашем сайте.
❓ Вопросы и ответы
Сейчас мы представим ответы на вопросы, которые часто возникают по данной теме.
Что такое цилиндр?
Цилиндр — это геометрическая фигура, которая имеет два плоских основания, обычно круглой формы, и боковую поверхность, которая состоит из параллельных прямых линий.
Как вычислить объем цилиндра?
Объем цилиндра можно вычислить, используя формулу:
V = πr²h
где V – объем цилиндра, π – число Пи (приблизительно равно 3.14), r – радиус основания цилиндра и h – высота цилиндра.
Можно ли использовать формулу объема цилиндра для вычисления объема других фигур?
Нет, формула объема цилиндра может использоваться только для вычисления объема цилиндра. Для других фигур существуют свои собственные формулы для расчета объема.
Как найти радиус или диаметр цилиндра, если они неизвестны?
Если известна площадь основания цилиндра, можно найти радиус, используя формулу:
r = √(A/π)
где A – площадь основания цилиндра.
Если известен объем цилиндра, можно найти радиус, используя формулу:
r = √(V/πh)
где V – объем цилиндра, h – высота цилиндра.
Диаметр можно найти, удваивая радиус.
Как найти объем трубы или канала?
Для трубы или канала формула для вычисления объема имеет немного другой вид:
V = πr²h
где V – объем, r – радиус, h – длина (высота) трубы или канала.
Например, если радиус трубы равен 10 см, а длина трубы составляет 2 м, то объем трубы будет:
V = 3.14 * 10² * 200 = 62,800 см³, что равно 62.8 литрам.
Как узнать, сколько литров вмещает бочка?
Чтобы узнать, сколько литров вмещает бочка, нужно знать ее объем. Если известны диаметр и высота бочки, то можно использовать формулу для объема цилиндра. Например, если диаметр бочки составляет 1 метр, а высота – 1,5 метра, то ее объем будет:
V = πr²h = 3.14 * (1/2)² * 1.5 = 1.18 кубических метров, что равно 1180 литрам. Таким образом, бочка вмещает 1180 литров жидкости.
Как узнать, сколько литров вмещает труба?
Для расчета объема трубы нужно знать ее длину и радиус. Если известны диаметр и длина трубы, то радиус можно найти, разделив диаметр на 2. Например, если диаметр трубы составляет 10 см, а длина трубы – 2 метра, то радиус будет 5 см. Тогда объем трубы можно найти, используя формулу:
V = πr²h = 3.14 * (5/100)² * 200 = 15.7 литров. Таким образом, труба вмещает 15.7 литров жидкости.
Какой тип калькулятора нужен для расчета объема цилиндра?
Для расчета объема цилиндра нужен специальный калькулятор, который может выполнить математические операции с использованием формулы для объема цилиндра.
Какие значения нужно ввести в калькулятор объема цилиндра?
Для расчета объема цилиндра необходимо ввести значение радиуса основания цилиндра и высоты цилиндра.
Какие единицы измерения могут использоваться при вводе значений в калькулятор объема цилиндра?
Единицы измерения, которые могут использоваться при вводе значений в калькулятор объема цилиндра, это сантиметры, метры, дюймы и т.д.
Какие дополнительные функции могут быть включены в калькулятор объема цилиндра?
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
Где можно найти калькулятор объема цилиндра?
Калькулятор объема цилиндра можно найти в Интернете на специализированных сайтах, в приложениях для мобильных устройств и на компьютерах, а также в других программных приложениях, связанных с инженерными и научными расчетами.
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Диаметр и высота цилиндра
Свойства
Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD
Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD
Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD
Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD
Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD
Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
[spoiler title=”источники:”]
http://poschitat.online/diametr-okruzhnosti
http://skysmart.ru/articles/mathematic/diametr-okruzhnosti
[/spoiler]
Содержание
- – Как найти середину диаметра?
- – Какой диаметр центра?
- – Каковы конечные точки диаметра?
- – Что вы называете центром круга?
- – Какое уравнение стандартной формы представляет собой круг?
- – Какую формулу вы должны использовать, чтобы найти центр круга с учетом двух конечных точек диаметра?
Как найти середину диаметра?
Предполагая, что у вас есть конечная точка диаметра круга, вы можете использовать формулу средней точки, чтобы найти точка на полпути между двумя точками. Согласно определению диаметра, это будет центральная точка круга. Если у вас есть точки (x1, y1) и (x2, y2), формула средней точки будет (x1 + x22, y1 + y22).
Какой диаметр центра?
Диаметр – это хорда, проходящая через центральную точку круга. Это самый длинный аккорд любого круга. Центр круга середина его диаметра. То есть делит его на две равные части, каждая из которых представляет собой радиус круга.
Каковы конечные точки диаметра?
Диаметр круга – это любой отрезок прямой, который проходит через центр круга и концы которого находятся на окружности круга. Указанные конечные точки диаметра равны (−2,4) и (4,8) .
Что вы называете центром круга?
Центр круга также называют фокус круга.
Какое уравнение стандартной формы представляет собой круг?
Учитывая окружность на координатной плоскости, Сал находит свое стандартное уравнение, которое представляет собой уравнение в форме (x-a) ² + (y-b) ² = r².
Какую формулу вы должны использовать, чтобы найти центр круга с учетом двух конечных точек диаметра?
(x − h) 2+ (y − k) 2 = r2 (x – h) 2 + (y – k) 2 = r 2 – это форма уравнения для окружности с радиусом r и (h, k) в качестве центра точка. В этом случае r = √26, а центральная точка находится в (2,7). Уравнение для круга: (x− (2)) 2+ (y− (7)) 2 = (√26) 2 (x – (2)) 2 + (у – (7)) 2 = (26) 2.
Интересные материалы:
Продаются ли американские автомобили в России?
Продаются ли Форды в России?
Продать или разобрать серебряное янтарное колье?
Продавать золото – хорошая идея?
Продажи падают в январе?
Продолжают ли расти горбинки на спине?
ProduKey – это вирус?
Продукция Bosch производится в Германии?
Профессиональные геймеры используют ПК или консоль?
Профессионалы используют Photoshop?
3.3 средний диаметр: Среднеарифметическое наибольшего и наименьшего значений диаметров, измеренных в одном поперечном сечении, перпендикулярном к оси трубы.
3.2 средний диаметр: Среднеарифметическое наибольшего и наименьшего значений диаметров, измеренных в одном поперечном сечении, перпендикулярном к оси трубы.
3.23 средний диаметр (mean diameter): Среднее значение диаметра для данного диапазона размеров, выраженное в мкм.
22 средний диаметр: Диаметр среднего конуса или расстояние между средними линиями резьбы по нормали к оси резьбы.
Смотри также родственные термины:
Средний диаметр прокладки, мм (см)
Dс.п
3.1.37 средний диаметр конической резьбы: Диаметр в основной плоскости или заданном сечении воображаемого прямого кругового конуса, соосного с конической резьбой, каждая образующая которого пересекает профиль резьбы таким образом, что проекции на ось резьбы отрезков, образованных при пересечении с впадиной, равны половине номинального шага резьбы.
70. Средний диаметр конической резьбы
Средний диаметр резьбы
D. Flankendurchmesser des kegligen Gewindes
d2, D2
Диаметр в основной плоскости или в заданном сечении воображаемого прямого кругового конуса, соосного с конической резьбой, каждая образующая которого пересекает профиль резьбы таким образом, что проекции на ось резьбы отрезков, образованных при пересечении с канавкой, равны половине номинального шага резьбы (см. черт. 32)
15. Средний диаметр общего звена – среднее значение двух взаимно перпендикулярных диаметров сечения звена плоскостью, перпендикулярной образующей внешнего контура звена в любом его месте.
3.4.1.6 средний диаметр отверстия (в основном цилиндрического отверстия) dm: Среднеарифметическое значение наибольшего и наименьшего единичных диаметров отверстия отдельного кольца
dm = (ds max + ds min)/2.
3.4.1.8 средний диаметр отверстия в единичной плоскости dmp: Среднеарифметическое значение наибольшего и наименьшего единичных диаметров отверстия в единичной радиальной плоскости
dmp = (dsp max + dsр min)/2.
3.4.1.15 средний диаметр отверстия комплекта тел качения (радиальный подшипник без внутреннего кольца) Fwm:Среднеарифметическое значение наибольшего и наименьшего единичных диаметров отверстия комплекта тел качения
Fwm = (Fws max + Fws min)/2.
4. Средний диаметр площади контакта молотка ударной машины с поверхностью образца (dср)
Средняя величина, получаемая в результате двухкратного измерения (в двух взаимно перпендикулярных направлениях) диаметра площади отпечатка, получающегося при соприкосновении падающего молотка ударной машины с поверхностью образца покрытия
Средний диаметр прокладки, мм
Dсп
Средний диаметр прокладки, мм (см)
Dс.п
3.1.3 средний диаметр резьбы: Диаметр воображаемого, соосного с резьбой, прямого кругового цилиндра, каждая образующая которого пересекает профиль резьбы таким образом, что ее отрезки, образованные при пересечении с канавкой, равны половине номинального шага резьбы.
31. Средний диаметр цилиндрической резьбы
Средний диаметр резьбы
D. Flankendurchmesser des Gewindes
E. Pitch diameter, simple pitch diameter
F. Diamètre sur flancs, diamètre mesuré sur flancs
d2, D2
Диаметр воображаемого, соосного с резьбой прямого кругового цилиндра, каждая образующая которого пересекает профиль резьбы таким образом, что ее отрезки, образованные при пересечении с канавкой, равны половине номинального шага резьбы (черт. 15)
Черт. 15
24. Средний диаметр частиц
Средний линейный размер совокупности полидисперсных частиц твердой фазы сферической или неправильной формы, без значительной разницы между линейными размерами этих частиц
Словарь-справочник терминов нормативно-технической документации.
.
2015.