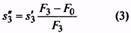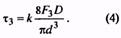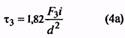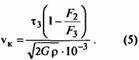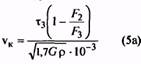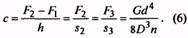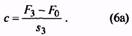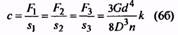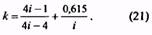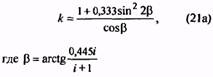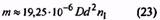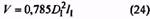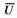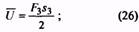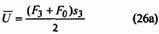Сам оригинал размещен вот тут: http://www.pirate4x4.com/tech/billavista/coilovers/Part_1/#DualRateSprings
Не уверен, что там будет что новое со времен известной книги Рампеля. Но всетаки… по мимо этого буду что то от себя писать , где то что то добавлять..
Начну не с начала, там рассказывается об устройстве амортизатора, двух трубные, однотрубные и т.д. То, что идет дальше – поинтереснее.
Теория пружин
В койловерах применяются пружины сжатия. Для дальнейших рассуждений определимся с обозначениями пружин и основными их характеристиками:

- Внутренний диаметр (Di)
- Диаметр витка (Dw)
- Средний диаметр пружины (Dm)
- Количество активных витков пружины (Na)
- Коэффициент жесткости пружины (k)
- Высота в свободном состоянии (Lo)
- Высота в сжатом состоянии(Lc)
- Ход пружины (Sc)
- Предельная нагрузка (Fc)
Рассмотрим каждый из параметров:
Внутренний диаметр (Di)
Тут все элементарно: пружина должна одеваться на амортизатор, т.е. в случае койловеров 3″ пружина идет на 2,5″ амортизатор, а 2,5″ пружина на 2″ амортизатор. Это основное, почему нас будет интересовать внутренний диаметр.
Диаметр витка (Dw)
Диаметр “проволоки” из которой сделана пружина.
Средний диаметр пружины (Dm)
Диаметр пружины измеренный по оси “проволоки
“, из которой изготовлена пружина. Видно, что справедливо равенство: Dm = Di + Dw
Количество активных витков пружины (Na)
Количество активных витков пружины показывает какой количество витков воспринимает нагрузку. Обычно это число равно полному количеству витков пружины за минусом двух. Эти два витка, не дают вклада в общую жесткость пружины.
Жесткость пружины (k)
Самая важная характеристика пружины – это ее жесткость. Она показывает: какую силу необходимо приложить к пружине вдоль ее оси, чтобы ее линейные размеры изменились на 1мм. (Буду сразу все переводить в систему СИ)
На жесткость пружины влияют следующие параметры:
1. Материал, из которого изготовлена пружина.(параметр отражающий это называется модуль кручения. Модуль кручения показывает какую силу необходимо приложить к образцу, чтобы закрутить его на угол в 1 рад. )
2. Диаметр витка “проволоки” из которой изготовлена пружина (Dw).
3. Средний диаметр пружины (Dm)
4. Количество активных витков пружины (Na)
Формула расчета коэффициента жесткости пружины:
k = G * (Dw)^4 / 8 * Na * (Dm)^3
,где G – модуль сдвига (для обычной стали G ≈ 80 ГПа, для пружинной стали G ≈ 78500 МПа, как пример для меди ~ 45 ГПа)
(небольшое отступление… в оригинале статьи использовали термин “torsional modulus”(модуль кручения), вместо термина модуль сдвига, это разные вещи). Модуль сдвига это отношение касательного напряжения к сдвиговой деформации, т.е. G = (действующая сила/площадь, на которую сила действует) / (смещение / начальная длинна). Формула немного сложная для понимания, но, если учесть, что модуль сдвига есть в таблицах и нет необходимости его высчитывать, то все встает на свои места. В исходном тексте статьи приведен пример, где G = 11250000psi, если перевести в Па, то получим 77,57ГПа (практически наша пружинная сталь, но в оригинале статьи упоминается какая то сталь без указания марки с повышенным содержанием хрома и углерода)
При внимательном рассмотрении формулы расчета коэффициента жесткости пружины мы увидим, что на жесткость влияет прежде всего (при одном и том же модуле сдвига) средний диаметр пружины, количество витков и диаметр витка “проволоки” из которой изготовлена пружина. Эти параметры можно изменять, если необходимо получить пружину различной степени жесткости. Причем следует заметить, что диаметр витка идет в четвертой степени, а количество витков – в первой. Т.е. различные параметры дают разные вклады в результат.
Дальше в оригинале статьи приводится табличка, в которой наглядно показано что как изменяется, при изменении членов этого уравнения. Мы тут все русские люди, изучавшие математику в школе и прекрасно понимающие как работают дроби, позвольте мне тут эту таблицу не приводить и так все понятно.
Идем дальше. Если мы рассматриваем пружину, которая уже установлена в койловер, то совершенно понятно, что при выбранной марке стали диаметр тоже будет постоянным, т.е. у нас остается только два параметра для изменения жесткости пружины – диаметр “проволоки” из которой изготовлена пружина и количество витков. Причем обратите внимание, что диаметр “проволоки” из которой изготовлена пружина влияет сильнее, чем количество витков. И напоследок еще одна мысль: получается, что при заданном диаметре пружины, если нам необходимо сделать пружину жестче, то нам надо или уменьшить количество витков, или использовать более толстую “проволоку” для изготовления пружины. И наоборот, для того, чтобы пружина получилась менее жесткая, необходимо или увеличивать количество витков, или изготавливать пружину из более тонкой “проволоки”.
Точно так же, глядя на формулу мы видим, что увеличение диаметра при прочих одинаковых параметрах ведет к увеличению жесткости пружины и наоборот.
Таким образом можно для себя отметить важные моменты:
1. При заданных длине и диаметре пружины менее жесткая пружина будет иметь большее количество витков, и как следствие меньший ход. Т.е. для сохранения величины хода менее жесткую пружину необходимо делать выше.
2. При заданной жесткости пружины и ее высоте больший диаметр пружины (которая требуется для большего в диаметре амортизатора) будет иметь меньшее количество витков и как следствие больший ход.
Представленные на рынке пружины имеют разную высоту, диаметр и жесткость. Но при этом надо принять во внимание, что разница между 2,5″ и 3″ пружинами при одинаковой жесткости и высоте по остальным параметрам столь не значительна, что в этом случае диаметр не может являться основным фактором, на основе которого принимают решение о покупке того или иного варианта.
Практически жесткость пружины можно узнать непосредственно измерив соответствующие значения: (кг/мм) = Сила(кг)/Деформация(мм)
Жесткость пружины может быть постоянной величиной или переменной (имеется в виду зависимость от деформации). Пружины, которые не меняют свою жесткость от деформации получили название линейные (*) Также существуют пружины, которые изменяют свою жесткость в зависимости от деформации, это так называемые прогрессивные пружины. Как правило прогрессивные пружины имеют разный диаметр витков по высоте. Здесь мы не будем рассматривать такие пружины, т.к. в койловерах они не применяются.
(*)В действительности же, если мы начнем измерять жесткость линейной пружины, то в первые и последние 10% ее хода жесткость будет отливаться от остальных 80%. Этот момент так же приходится учитывать.
Высота в свободном состоянии (Lo)
Высота в свободном состоянии это измеренная высота пружины, на которую не действует нагрузка. Теоретически задается производителем при изготовлении пружины.
Существует зависимость количества витков пружины, которые можно изготовить от диаметра пружины. Например, слишком длинная пружина при небольшом диаметре не будет деформироваться под нагрузкой как задумано, что приведет к невозможности выполнять свои функции в полной мере. Именно по этой причине 18″ пружины диаметром 3″ существуют, а диаметром 2″ их нет.
Для создания пружины с различной высотой в свободном состоянии, но с одинаковой жесткостью производитель просто увеличивает расстояние между витками. Т.е. параметры: диаметр проволоки, из которой изготовлена пружина, диаметр витка и количество витков остаются без изменений, изменяется только высота в свободном состоянии.
При нормальной эксплуатации (т.е. при использовании пружины в условиях, которые предусматривал разработчик) высота пружины в свободном состоянии меняться не должна.
Высота в сжатом состоянии(Lc)
Высота в сжатом состоянии это высота,меньше которой пружина сжаться не в состоянии без ее разрушения. В этом состоянии витки пружины прижаты друг к другу.
Ход пружины (Sc)
Ход пружины это разница между высотой пружины в свободном состоянии и высотой пружины в сжатом состоянии.
Предельная нагрузка (Fc)
Предельная нагрузка это нагрузка, при превышении которой не происходит деформации пружины без ее разрушения. При приложенной предельной нагрузки к пружине измеряют высоту в сжатом состоянии. Именно предельная нагрузка вызывает смыкание витков пружины. Это очень важный параметр. Он говорит нам о том, какую максимальную нагрузку способна выдержать пружина вовремя своей работы. Без этой информации не обойтись при проектировании длинно ходовых подвесок, в которых необходимо сделать ход колеса максимальным.
Двойные пружины
Можно с уверенность сказать, что проектирование подвески это прежде всего поиск нужного баланса. С одной стороны пружина должна быть достаточно мягкая для перемещения по дорогам с большими ямами, выступами, хода подвески должно быть достаточно для компенсации перепадов рельефа. Пружина должна обеспечивать достаточный комфорт для перемещения по рельефу подобного типа. С другой стороны жесткость пружины должна быть достаточной для того, чтобы сохранить контроль при быстром движении по неровной дороге, прохождении поворотов, торможении и т.д. В общем жесткая пружина требуется именно тогда, когда мы говорим о скоростном перемещении.
Преимущество койловеров как раз и состоит в том, что в этой конструкции состоящей из двух пружин можно ближе всего приблизиться к этому балансу. Для того, чтобы продолжить описание дальше вспомним конструкцию стойки койловера:
Необходимо отметить, что положение ограничительного кольца(stop-ring) ограничивает ход dual rate slider (DRS), проставки, скользящей по корпусу, в которую с одной стороны упирается мягкая пружина, а с другой – жесткая. Т.е. положение ограничительного кольца ограничивает ход мягкой пружины и позволяет настраивать подвеску в зависимости от дорожных условий. Ограничительное кольцо располагают таким образом, чтобы максимальная жесткость достигалась от 60 до 80% хода амортизатора. При таком раскладе остается еще запас хода подвески, прежде чем в работу вступят отбойники.
Суммарную начальную жесткость составной пружины можно рассчитать как:
Ki = (Km * Kt) / (Km + Kt)
,где
Ki = суммарная начальная жесткость составной пружины
Km = жесткость мягкой пружины
Kt = жесткость жесткой пружины
Жесткость составной пружины, в случае, когда DRS уперлась в ограничительной кольцо, просто равняется жесткости жесткой пружины.
Kf = Kt
Примечание: в оригинале статьи введены понятие tender spring и main spring. Судя по фото main spring это мягкая пружина, tender spring это жесткая пружина. Но дальше в статье эти понятия были перепутаны, в частности в вышеприведенной формуле.
На этом про пружины хватить, определимся с некоторыми терминами и двинемся дальше:
Полная нагрузка колеса на поверхность (CW)
Усилие, с которым автомобиль давит на грунт одним из колес. Надо учесть, что это не просто общая масса автомобиля, поделенная на четыре. Данный параметр показывает распределение нагрузки автомобиля на поверхность.
Нагрузка от подрессоренной массы на одно колесо (CSW)
Нагрузка, которая приходится на каждую пружину. Так же как и предыдущий, указанный параметр показывает распределение нагрузки на подвеску.
Нагрузка от не подрессоренной массы на поверхность (CUW)
Нагрузка от не подрессоренной части автомобиля, приходящаяся на одно колесо. Можно сказать, что численно равно сумме масс: колеса в сборе, тормозному суппорту, половине массы моста, половине массы рычага, массе амортизатора и пружины.
Исходя из вышесказанного можно записать:
Нагрузка от подрессоренной массы на одно колесо (CSW) = Полная нагрузка колеса на поверхность (CW) – Нагрузка от не подрессоренной массы по поверхность(CUW)
Точка перехода(SUR)
Значение в процентах. Показывает в какой момент в составной пружине начинает работать жесткая часть.
SUR = Жесткость жесткой пружины / Жесткость составной пружины* 100% = (Kf / Ki) *100%
Ход амортизатора (ST)
Максимальный ход амортизатора определяется разностью размеров полностью сжатого и максимально открытого амортизатора. Койловеры диаметром 2″ имеют ход 14″, 16″ и 18″.
При выполнении измерений на предмет того – какие амортизаторы необходимо приобрести, важно понимать, что ход колеса и ход амортизатора это разные вещи. Они могут отличаться, и очень сильно.
Для ограничения хода подвески не рекомендуется использовать физический возможности амортизатора. Для ограничения хода подвески лучше всего использовать специальные ремни и демпферы.
Максимальное раскрытие амортизатора (ход отбоя вверх)
Максимальное раскрытие амортизатора , как следует из названия наступает при его полном ходе. Если никаких мер не предпринято и амортизатор ограничивает ход подвески вниз, то ежу понятно, что он скоро сломается. Не делайте так, если любите свою машину.
Максимальное сжатие амортизатора (ход отбоя вниз)
Как говорится и ежу понятно, что данное состояние наступает, когда у нас амортизатор полностью сжат. И Здесь так же по аналогии, если Вы любите и заботитесь о своем автомобиле – не делайте так, чтобы амортизатор ограничивал ход подвески “вверх” – ни к чему хорошему это не приведет. Кстати, на некоторый койловерах на шток одет маленький резиновый демпфер. Запомните – он не для того, чтобы гасить удары подвески “до отбойника” – не надейтесь на него!!!
Возрастающая жесткость
Термин имеет отношение к элементам подвески, которые дают свой положительный вклад в жесткость, это могут быть, к примеру демпферы, пружины, подрессорные листы и т.д. Термин известен, как прогрессирующая жесткость.
Уменьшающаяся жесткость
Как не трудно догадаться это полная противоположность возрастающей жесткости. Т.е. есть элементы, жесткость которых падает по мере хода подвески. Термин известен как регрессирующая жесткость.
Выше мы уже упоминали о том, что ход пружины, амортизатора и колеса это три разных вещи (если мы рассматриваем койловеры, то ход пружины и амортизатора равны, в остальных случаях это не так). Связаны эти вещи между собой кинематическими соотношениями, в которых важно все – и угол между пружиной и рычагом и место расположения амортизатора…. Все это влияет на эффективность работы амортизатора и пружины…А в конечном счете это приводит массе других следствий: от взаимного положения элементов подвески зависит курсовая устойчивость, управляемость и комфорт пассажиров.
Дальше мы будем говорить как раз об углах, размерностях и взаимном положении отдельных элементов подвески.
Теория подвески
Очень редко бывает ситуация, когда пружина вместе с амортизатором находится около колеса и колесо во время движения совершает строго вертикальные перемещения. Это идеальная ситуация, не всегда она возможна из за особенностей конструкции автомобиля. Во всех остальных случаях мы говорим об эффективности работы того или иного узла подвески.
Из общего курса физики известно, что совершенная работа представляет собой произведение развиваемого усилия на расстояние, которое было преодолено за счет этого усилия, т.е. можно записать: W = F x d. Самый важный для нас вывод из этого уравнения состоит в том, что одну и ту же работу можно совершить прилагая различные усилия, соответственно изменяя расстояние. Наглядный пример вышесказанного: реечный домкрат. Работа по подъему автомобиля на 1 метр постоянна, но человек без использования рычажной системы домкрата не в состоянии ее совершить. Т.е., проиграв в расстоянии, т.е. уменьшив прилагаемое усилие и увеличив расстояние (в нашем случае это количество движений рычагом реечного домкрата, мы способны поднять автомобиль. Т.е. в соответствии с законом сохранения энергии выиграв в чем то одном, мы обязаны проиграть в другом.
Графически эту ситуацию можно представить в следующем виде:
,где F1- нагрузка, F2- развиваемое усилие, fulcrum -точка равновесия, d2 -рычаг развиваемого усилия, d1- рычаг действующей нагрузки. Используя эти обозначения и закон сохранения энергии можно записать:
Load * Load Arm = Effort * Effort Arm, или F1*d1 = F2*d2
, отсюда находим, какое усилие необходимо приложить, чтобы уравновесить нагрузку:
F1 = (F2 * d2) / d1
Совершенно понятно, что основное свойство рычажного механизма, это соотношения длин рычагов, т.е. в нашем случае MA = d2/d1. Назовем этот параметр механическим выигрышем.
Если взглянуть на вот этот рисунок:
,то сразу видно в чем проигрываем, выигрывая в развиваемой силе. Мы проигрываем в том пути, который необходимо преодолеть. Назовем это Выигрышем в перемещении (DR). Совершенно понятно, что DR=1/MA. Т.е. присутствует обратная зависимость.
По расположению точки опоры можно выделить три рычажные системы:
Первая, известная нам классическая схема. Не трудно видеть, что перемещая точку опоры мы либо выигрываем в силе, проигрывая в расстоянии, либо наоборот: все в соответствии с законом, который мы рассмотрели ранее.
Переместив нагрузку в середину рычажной системы, а точку опоры к одному из ее концов,мы получим второй тип:
Изучая соотношения MA = d2/d1 и DR = d1/d2 для этого случая, не трудно заметить, что тут прежде всего реализуется ситуация с выигрышем в силе и, соответственно, проигрышем в пути. Таким образом, значение нагрузки всегда будет больше значения приложенной силы и соответственно, пути также будут различными. Другими словами, используя введенные ранее обозначения, можно записать: MA >=1 и DR <=1.
Кстати, если Вы повнимательнее взгляните на последний рисунок и включите фантазию, то увидите, что это по сути и есть рычаг подвески. Более плотно мы коснемся этого чуть дальше.
Поменяв местами точки приложения нагрузки и усилия из предыдущего класса, мы получаем третий тип:
Здесь, как не трудно заметить, реализуется обратная ситуация: мы выигрываем в перемещении, но проигрываем в усилии. Т.е. в этом случае MA <=1 и DR >=1.
Сведем полученные данные в одну таблицу для наглядности:
| Класс | В чем проигрываем | В чем выигрываем | Примечание | Пример |
| 1 | Перемещение | Сила | Для случая, когда точка опоры расположена таким образом, что d2 > d1 | Консервный нож |
| 1 | Сила | Перемещение | Для случая, когда точка опоры расположена таким образом, что d2 < d1 | Катапульта |
| 2 | Перемещение | Сила | Тачка, Дверь | |
| 3 | Сила | Перемещение | Метла, Бейсбольная бита |
Итак, подведем еще раз основные итоги: используя рычаг можно совершить одну и ту же работу при различных перемещениях и усилиях. причем эти вещи обратны, т.е. выигрывая в одном, мы проигрываем в другом. Соответственно применительно к подвеске автомобиля можно видеть, что перемещение крепления колеса и амортизатора на рычаге приводит к различным последствиям в свете вышесказанного.
Влияние угла
Ранее мы с Вами увидели, что рычажная система может приводить к разнице ходов колеса и амортизатора. Аналогичным образом различные взаимные углы установки рычагов, амортизаторов и колес могут приводить к различным ходам этих элементов подвески.
Если мы установим амортизатор вертикально, так, как показано на картинке:
, то можно с уверенностью сказать, что ход колеса будет равняться ходу амортизатора, т.е. если колесо сместилось на 1см, то и точка крепления амортизатора переместится на это расстояние.
Рассмотрим другой, гипотетический вариант, реально так конечно же не делает, но для наглядности этот пример привести можно:
Видно, что любое перемещение колеса не приведет к сколько нибудь заметному сжатию амортизатора или пружины.
Теперь предлагаем для полноты картины рассмотреть промежуточный вариант, когда амортизатор установлен под углом в 45°:
Если немного углубиться в тригонометрию, то можно увидеть, что ход колеса в этом случае и ход места крепления амортизатора не будут совпадать. Ход амортизатора будет несколько меньшим в этом случае. Для удобства обозначим угол между вертикалью и штоком амортизатора как “alpha”, а косинус этого угла назовем фактором угла и обозначим через ACF, таким образом: ACF = cos(alpha)
Теперь мы знаем два фактора, которые влияют на разницу ходов колеса и амортизатора:
DR = d1/d2
ACF = cos(alpha)
Для дальнейшего удобства давайте введем еще один показатель который будет линейной комбинацией этих двух и назовем его установочным фактором. Он будет в полной мере отражать разницу между ходом колеса и ходом точки крепления амортизатора на рычаге:
IR = DR * ACF
Для краткости давайте в дальнейшем условимся называть параметр “место крепления уха амортизатора и угол относительно вертикали” просто “геометрия установки амортизатора”.
Установочный фактор
Суммируя вышесказанное, можно утверждать, что установочный фактор связывает ход колеса с ходом амортизатора (пружины) следующим образом:
ST = WT * IR, отсюда следует: WT = ST / IR, IR = ST / WT
IR = DR * ACF;
при этом:
DR = d1/d2;
ACF = cos(alpha)
Т.е. все что нам необходимо знать для того, чтобы рассчитывать ход колеса при заданной геометрии, или наоборот, ход у амортизатора при заданном ходе колеса, это расстояния d1, d2 и угол alpha.
Если нам известно значение IR, то мы можем вычислить и некоторые другие параметры:
- Максимально возможный ход колеса при заданной геометрии амортизатора.
- Подбор конкретного амортизатора для заданного хода колеса и заданной геометрии амортизатора.
- Определение необходимой геометрии установки амортизатора, для того, чтобы получить необходимый ход колеса при заданном амортизаторе.
И, разумеется, этому параметру можно придумать еще массу применений.
Надо заметить, что точно также как ход пружины зависит от геометрии ее установки, точно также результирующая жесткость пружины зависит от геометрии ее установки. Называют такую жесткость эффективной или жесткостью на колесе. Ее принято обозначать как (WR).
Геометрия установки пружины определяем несколько важных характеристик автомобиля:
- Высоту кузова автомобиля при заданной подрессоренной массе в пересчете на одно колесо автомобиля.
- Эффективность подвески в общем случае. Этот параметр показывает, как колесо будет реагировать на различные неровности на дороге. Насколько в конечном счете автомобиль будет управляемым и конечно же этот параметр позволяет определить – достаточна ли жесткость подвески.
В зависимости от класса рычажной системы можно наблюдать переход усилия в перемещение и наоборот. Это имеет отношение и к перемещению колеса и ходу амортизатора, рассчитать можно практически все взаимосвязи между элементами рычажной системы.
Объединяя вышеприведенные формулы, получим:
IR = DR * ACF = (d1/d2) * cos(alpha)
Необходимо отметить, что т.к. все эти изменения линейны, то мы можем свободно говорить о том, что знаем изменение развиваемого усилия, или жесткости, при том, что нам известны расстояния, т.е. в общем случае разница между ними.
Теперь сделаем еще один шаг и посчитаем жесткость пружины, измеряемой на колесе при том, что у нас известна геометрия подвески. Очевидно, что выглядеть это будет следующим образом:
WR = k * IR * IR
или
WR = k * IR^2
,где
WR = жесткость пружины, измеренная на колесе(кг/мм)
K = жесткость пружины (кг/мм);
IR = установочный фактор.
Суммирование
Давайте еще раз перечислим те знания, которые мы получили выше, и которые относятся к рычажным механизмам.
1.Мы знаем что такое и как работает рычажная система: на что влияет разница в длинах рычагов и как на это влияет расположение точки опоры. Другими словами, мы знаем как осуществляется переход перемещения в силу и наоборот.
2.Мы знаем, что подвеска также является рычажной системой между колесом и пружиной и на перевод перемещения в силу и наоборот влияет геометрия подвески: установочные углы отдельных ее элементов и т.д.
3.Мы узнали, что существует т.н. установочный фактор (IR), который в себе содержит информацию о геометрии подвески автомобиля.
4.Мы узнали, что усилие, которое используется в формуле рычажной подвески может быть разным, т.е. это может быть и развиваемое усилие амортизатора, и усилие, которое развивает автомобиль и которое приходится на одно колесо.
5.Жесткость пружины, измеренная на колесе пропорциональна квадрату установочного фактора: WR = k * IR * IR = k* IR^2.
Сведем полученные формулы в таблицу:
| Номер | формула | Описание |
|---|---|---|
| 1 | MA = d2/d1 | Механический выигрыш есть отношение расстояний: приложения силы на расстояние, на котором размещен груз. |
| DR = d1/d2 | Выигрыш в расстоянии есть обратная величина механическому выигрышу. Т.е. отношение расстояний: размещения груза и точки приложения силы | |
| 2 | DR = d1/d2 | Выигрыш в расстоянии для подвески это расстояние от центра пружины то точки опоры рычага, деленное на расстояние от центра колеса до точки опоры рычага. |
| ACF = cos(alpha) | Чем больше угол, под которым установлена пружина (от вертикали), тем меньше жесткость подвески (измеренная в точке крепления колеса) | |
| IR = DR * ACF | Установочный фактор есть произведение выигрыша в расстоянии на угловой фактор. | |
| 3 | WT = ST / IR | Ход колеса это ход амортизатора, деленный на установочный фактор. |
| Fw = Fs * IR | Усилие, которое развивает пружина передается в точку крепления колеса с учетом установочного фактора. | |
| Установочный коэффициент определяет соотношение между силой и перемещением. | ||
| 4 | Fs = k * ST | Усилие, развиваемое пружиной, выраженное в килограммах есть жесткость пружины (выраженная в кг/мм), умноженная на перемещение пружины |
| Fw = WR * WT | Аналогично, усилие, выраженное в килограммах и измеренное в точке крепления колеса есть произведение жесткости(выраженной в кг/мм), измеренной в точки крепления колеса на величину перемещения колеса(выраженной в мм) | |
| 5 | WR = k * IR^2 | Давайте математически выведем это соотношение. Жесткость подвески, измеренная в точке крепления колеса, как известно, есть усилие, развиваемое в точке крепления колеса и деленное на перемещение колеса: WR = Fw / WT также мы знаем, что в точке крепления пружина развивает усилие, равное собственному усилию пружины, умноженное на установочный фактор Fw = Fs * IR Таким образом, мы можем записать: WR = Fs * IR / WT Идем дальше: перемещение колеса есть собственный ход пружины, деленный на установочный фактор: WT = ST / IR Подставив в предыдущую формулу перемещение колеса, выраженное через установочный фактор и ход пружины, получим: WR = (Fs * IR) / (ST / IR) Перепишем это соотношение несколько по другому: WR = (Fs * IR) * (IR / ST) И, наконец, так: WR = Fs / ST * IR * IR Соотношение Fs / ST есть ни что иное, как собственная жесткость пружины, т.е. k. Заменив соотношение жесткостью пружины, запишем: WR = k * IR * IR ,или WR = k * IR^2 Т.е. мы увидели, что жесткость пружины, измеренная в точке крепления колеса пропорциональна квадрату установочного фактора. |
Пять важных понятий
Вся эта вышеприведенная теория использует законы рычагов для того, чтобы связать между собой несколько вещей:
Это очень важные зависимости, давайте еще раз сведем их в отдельный список:
IR = Ds / Dw — установочный фактор, представляет из себя отношение хода пружины или амортизатора к ходу колеса.
Fw = Fs * IR — усилие, развиваемое пружиной в точке крепления колеса есть собственное значение развиваемого усилия пружиной, умноженное на установочный фактор.
Dw = Ds / IR — ход колеса есть ход пружины (или амортизатора), деленный на установочный фактор
Fs = k * Ds — усилие, развиваемое пружиной есть произведение жесткости пружины на ее ход.
Fw = WR * Dw — усилие жесткости пружины, выраженную в кг(т.е. при заданном смещении колеса) и измеренную в точке крепления колеса есть произведение хода колеса на жесткость пружины(выраженную в кг/мм), измеренную в точке крепления колеса.
Давайте еще раз суммируем полученные знания и рассмотрим на примерах:
Передаточное соотношение (DR)
Передаточное соотношение – это соотношение длин двух рычагов, находящихся во взаимодействии. Это соотношение описывает взаимосвязь между ходом колеса и ходом амортизатора через разницу длин соответствующих рычагов.
DR = d1/d2
Передаточное соотношение называть можно по разному, но суть от этого не меняется, как пример в английском варианте есть еще понятие “motion ratio” (MR)
Самый распространенный пример, это когда амортизатор закреплен между колесом и точкой опоры рычага (2 класс рычажной системы, который мы рассмотрели ранее)
d1 = расстояние между нижней точкой крепления амортизатора и точкой опоры рычага.
d2 = расстояние между точкой опоры колеса и точкой опоры рычага.
Фактор угла (или угловой коэффициент) (ACF)
Этот коэффициент показывает зависимость между ходом колеса и ходом амортизатора (установленного под определенным углом). При этом совершенно понятно, что если амортизатор установлен под углом, отличным от вертикального положения, то ход колеса всегда будет больше.
ACF = Cosine(alpha), где
alpha = угол установки амортизатора:
Если амортизатор установлен на оси моста, то alpha = это угол между осью амортизатора и вертикалью
Если амортизатор установлена на рычаге крепления моста, то alpha = это угол между осью амортизатора и линией, проведенной перпендикулярно к рычагу, на котором закреплен амортизатор (все это в случае. когда мы смотрим сбоку на это все, рычаги продольные, есть мост и т.д.).
Установочный фактор (IR)
Установочный фактор связывает перемещение колеса с перемещением амортизатора (пружины). Установочный фактор является линейной комбинацией передаточного соотношения и углового фактора. Он учитывает не только передаточное соотношение, но и угол установки амортизатора (все это вместе мы решили называть геометрией установки амортизатора):
IR = MR * ACF
Жесткость пружины, измеренная в точке крепления колеса (WR)
WR это эффективная жесткость пружины, измеренная в точке крепления колеса. Т.е. это жесткость пружины с учетом геометрии установки этой пружины, т.е. по аналогии с геометрией установки амортизатора. Жесткость пружины, измеренная точке крепления колеса есть произведение собственной жесткости пружины на квадрат установочного фактора:
WR = K * (IR)^2
В случае установки двух пружин (мы же договорились рассматривать по возможности все применительно к койловерам) можно говорить о начальной и конечной эффективной жесткости.
Начальная эффективная жесткость:
WRi = Ki * (IR)^2
, где Ki = начальная собственная жесткость составной пружины. IR = установочный фактор.
Конечная эффективная жесткость:
WRf = Km * (IR)^2
, где Km = конечная собственная жесткость составной пружины. IR = установочный фактор
И последнее, совершенно понятно, что если установить амортизатор по центру оси моста (или близко к этому) и строго вертикально (или близко к этому), то установочный фактор станет равен 1 (или близко к этому) и естественно им можно будет пренебречь в расчетах.
(продолжение следует)
Пружина
сжатия – это винтовая пружина с
фиксированным зазором между рабочими
витками способными выдержать работу
внешних сил противодействия, которые
рождаются в оси пружины.

Размеры
|
d |
диаметр |
|
D |
средний |
|
D1 |
наружный |
|
D2 |
внутренний |
|
H |
рабочая |
|
t |
шаг |
|
a |
расстояние |
|
sx |
деформация |
|
Lx |
длина |
|
Fx |
рабочая |
|
W8 |
энергия |
|
x |
индекс, |
Навивка
-
Вправо
(стандарт) -
Влево
(должна отображаться соответствующая
надпись)
Состояния
-
Свободное:
пружина не нагружена (индекс 0) -
Предварительная
нагрузка: пружина с минимальной рабочей
нагрузкой (индекс 1) -
Полная
нагрузка: пружина с максимальной рабочей
нагрузкой (индекс 8) -
Предел:
пружина вдавлена до касания витков
(индекс 9).
Расчетные
формулы для метрических единиц
Общие
формулы расчета
Коэффициент использования материала uS
Этот
коэффициент является отношением
напряжения при кручении полностью
нагруженной пружины к допустимому
напряжению при кручении, например
uS8 / A.
Чем больше величина коэффициента, тем
меньше материала уходит на изготовление
пружины и тем меньшими получаются ее
размеры и требуемое посадочное место;
однако, при этом становится хуже
эксплуатационная стабильность пружины.
Следовательно, коэффициент использования
материала обратно пропорционален
коэффициенту долговечности. Рекомендуемый
диапазон значений коэффициента
использования материала для обычных
рабочих условий: uS = 0,75 … 0,95.
Для пружин, применяемых в условиях
агрессивной среды, высоких температур
или ударной нагрузки, можно использовать
меньшие значения.
Запас прочности при пределе усталости kf
Этот
коэффициент используется при расчете
пружин с динамической нагрузкой (с
циклической усталостной нагрузкой при
сроке службы N > 105 рабочих
циклов). Он определяется отношением
предела выносливости пружины к напряжению
при кручении материала полностью
нагруженной пружины: kfe / 8.
Рекомендуемый диапазон значений запаса
прочности при предельной усталости
kf для стандартных рабочих
условий – от 1,1 до 1,5. Более высокие
значения kf обычно используются для
пружин, применяемых в условиях сильной
коррозии, высоких температур или ударной
нагрузки. Агрессивная среда оказывает
серьезное влияние на усталостную
прочность пружины, так как в результате
этого влияния допустимая нагрузка
пружины может снизиться до одной пятой,
в зависимости от материала и типа
агрессивной среды.
Наружный
диаметр пружины
D1 =
D + d [мм]
Где:
|
D |
средний |
|
|
d |
диаметр |
Внутренний
диаметр пружины
D2 =
D – d [мм]
Где:
|
D |
средний |
|
|
d |
диаметр |
Рабочая
деформация
H
= L1 –
L8 =
s8 –
s1 [мм]
Где:
|
L8 |
длина |
|
|
L1 |
длина |
|
|
s8 |
деформация |
|
|
s1 |
деформация |
Индекс
пружины
c
= D/d [-]
Где:
|
D |
средний |
|
|
d |
диаметр |
Поправочный
коэффициент Валя
![]()
Где:
|
c |
индекс |
|
|
d |
диаметр |
Общая
сила, действующая в пружине
![]()
Где:
|
d |
диаметр |
|
|
|
обобщенное |
|
|
D |
средний |
|
|
Kw |
поправочный |
|
|
G |
модуль |
|
|
s |
обобщенная |
|
|
n |
количество |
|
|
F0 |
начальное |
Жесткость
пружины
![]()
Где:
|
d |
диаметр |
|
|
F8 |
рабочее |
|
|
D |
средний |
|
|
H |
рабочая |
|
|
G |
модуль |
|
|
n |
количество |
|
|
F1 |
рабочее |
Средний
диаметр пружины
![]()
Где:
|
d |
диаметр |
|
|
k |
жесткость |
|
|
G |
модуль |
|
|
n |
количество |
Отклонение
пружины в большинстве случаев
s
= F / k [мм]
Где:
|
F |
Общая |
|
|
k |
жесткость |
Длина
пружины в свободном состоянии
L0 =
L1 +
s1 =
L8 +
s8 [мм]
Где:
|
L8 |
длина |
|
|
L1 |
длина |
|
|
s8 |
деформация |
|
|
s1 |
деформация |
Расчет
конструкции пружины
При
проектировании пружины подбирается
диаметр проволоки, количество витков
и длина свободной пружины L0 для указанной
нагрузки, материала и сборочных размеров
или диаметра пружины. Шаг резьбы пружины
в свободном состоянии с рекомендуемыми
диаметрами проволоки должен лежать в
диапазоне 0,3 D ≤ t ≤ 0,6 D [мм].
Конструкция
пружины определяется с учетом условия
прочности 8≤ us
A и
рекомендуемых диапазонов некоторых
геометрических параметров пружины:
L8 ≤ LminF и
D ≤ L0≤ 10
D и L0≤ 31,5
д. и 4 ≤ D/d ≤ 16 и n≤ 2 и 12
d ≤ t < D
Где:
|
D |
средний |
|
|
d |
диаметр |
|
|
шаг |
шаг |
|
|
8 |
напряжение |
|
|
A |
допустимое |
|
|
us |
коэффициент |
|
|
L8 |
длина |
|
|
LminF |
предельная |
|
|
n |
количество |
Если
в спецификации указаны условия
безопасности при изгибе и условия
проверки для усталостной нагрузки, они
учитываются при проектировании пружины.
В
следующем списке приведены процедуры
различных типов проектирования пружины.
Процедуры
разработки
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
10. Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в ред. 1990г.
Пружина сжатия
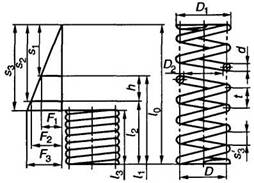
Пружина растяжения
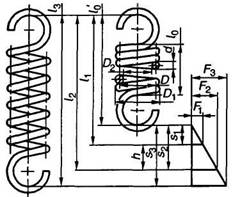
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
1. Сила пружины при предварительной деформации, Н |
F1 |
Принимаются в зависимости от нагрузки пружины |
|
2. Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н |
F2 |
|
|
3. Рабочий ход пружины, мм |
h |
|
|
4. Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с |
Vmax |
|
|
5. Выносливость пружины, число циклов до разрушения |
NF |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
6. Наружный диаметр пружины, мм |
D1 |
Предварительно назначают с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
7. Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации |
δ |
δ = 1-F2/F3. (1) Для пружин сжатия классов I и IIδ=0,05…0,25; для пружин растяжения δ=0,05…0,10; для одножильных пружин класса IIIδ=0,10…0,40; для трехжильных класса IIIδ=0,15…0,40 |
|
8. Сила пружины при максимальной деформации, Н |
F3 |
F3=F2/(1-δ) (2) Уточняется по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
9. Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н |
F0 |
F0= (0,1… 0,25) F3 |
|
10. Диаметр проволоки, мм |
d |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86 |
|
11. Диаметр трехжильного троса, мм |
d1 |
|
|
12. Жесткость одного витка пружины, Н/мм |
c1 |
|
|
13. Максимальная деформация одного витка пружины, мм |
s’3 (при F0=0) s”3 (при F0>0) |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86
|
|
14. Максимальное касательное напряжение пружины, Н/мм2 (Коэффициент k см. п. 35) |
τ3 |
Назначается по табл. 2 ГОСТ 13764-86. При проверке
Для трехжильных пружин
|
|
15. Критическая скорость пружины сжатия, м/с (Максимальная скорость подвижного звена механизма vmax должна быть равна или меньше vK, т.е. vK > vmax) |
vк |
Для трехжильных пружин
|
|
16. Модуль сдвига, Н/мм2 |
G |
Для пружинной стали G = 7,85·104 |
|
17. Динамическая (гравитационная) плотность материала, Н·с2/м4 |
Р |
p = γ/g, где g-ускорение свободного падения, м/с2; γ – удельный вес, Н/м3. Для пружиннойстали р = 8·103 |
|
18. Жесткость пружины, Н/мм |
с |
Для пружин с предварительным напряжением
Для трехжильных пружин
|
|
19. Число рабочих витков пружины |
n |
n = c1/c (7) |
|
20. Полное число витков пружины |
n1 |
n1 = n+ n2, (8) где n2 – число опорных витков |
|
21. Средний диаметр пружины, мм |
D |
D = D1 – d = D2 + d Для трехжильных пружин D = D1– d1= D2+ d1(9a) |
|
22. Индекс пружины |
i |
i = D/d (10) Для трехжильных пружин i= D/d1 (10а) Рекомендуется назначать от 4 до 12 |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
||||
|
23. Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки |
Δ |
Для трехжильного троса с углом свивкиβ=24° определяется по таблице, приведенной ниже |
||||
|
i |
40 |
45 |
50 |
55 |
60 |
7,0 и более |
|
Δ |
1,029 |
1,021 |
1,015 |
1,010 |
1,005 |
1,000 |
|
24. Предварительная деформация пружины, мм |
s1 |
s1=F1/c (11) |
||||
|
25. Рабочая деформация пружины, мм |
s2 |
s2= F2/c (12) |
||||
|
26. Максимальная деформация пружины, мм |
s3 |
s3= F3/c (13) |
||||
|
27. Длина пружины при максимальной деформации, мм |
l3 |
l3 = (n1 + 1 – n3)d, (14) где n3 – число обработанных витков. Для трехжильных пружин l3 = (n + l)d1Δ. (14а) Для пружин растяжения с зацепами l3 = l0 + s3 |
||||
|
28. Длина пружины в свободном состоянии, мм |
l0 |
l0=l3+s3 (15) |
||||
|
29. Длина пружины растяжения без зацепов в свободном состоянии, мм |
l0‘ |
l0‘ = (n1+1)d (15а) |
||||
|
30. Длина пружины при предварительной деформации, мм |
1l |
l1 = l0-s1. (16) Для пружин растяжения l1= l0+s1(16а) |
||||
|
31. Длина пружины при рабочей деформации, мм |
l2 |
l2=l0-s2. (17) Для пружин растяжения l2=l0+s2 (17а) |
||||
|
32. Шаг пружины в свободном состоянии, мм |
t |
t = s’3+d. (18) Для трехжильных пружин t = s’3+d1Δ. (18а) Для пружин растяжения t = d(18б) |
||||
|
33. Напряжение в пружине при предварительной деформации, Н/мм2 |
τ1 |
|
||||
|
34. Напряжение в пружине при рабочей деформации, Н/мм2 |
τ2 |
|
||||
|
35. Коэффициент, учитывающий кривизну витка пружины |
k |
Для трехжильных пружин
|
||||
|
36. Длина развернутой пружины (для пружин растяжения без зацепов), мм |
l |
|
||||
|
37. Масса пружины (для пружин растяжения без зацепов), кг |
m |
|
||||
|
38. Объем, занимаемый пружиной (без учета зацепов пружины), мм3 |
V |
|
||||
|
39. Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм |
λ |
Устанавливается в зависимости от формы опорного витка |
||||
|
40. Внутренний диаметр пружины, мм |
D2 |
D2=D1-2d (25) |
||||
|
41. Временное сопротивление проволоки при растяжении, Н/мм2 |
Rm |
Устанавливается при испытаниях проволоки или по ГОСТ 9389-75 и ГОСТ 1071-81 |
||||
|
42. Максимальная энергия, накапливаемая пружиной, или работа деформации, МДж |
|
Для пружин сжатия и растяжения без предварительного напряжения
для пружин растяжения с предварительным напряжением
|
Методика определения размеров пружин по ГОСТ 13765-86.
1. Исходными величинами для определения размеров пружин являются силы F1 и F2, рабочий ход h, наибольшая скорость перемещения подвижного конца пружины при нагружении или при разгрузке vmах, выносливость NF и наружный диаметр пружины D1 (предварительный).
Если задана только одна сила F2, то вместо рабочего хода h для подсчета берут величину рабочей деформации s2, соответствующую заданной силе.
2. По величине заданной выносливости NF предварительно определяют принадлежность пружины к соответствующему классу по табл. 1.
3. По заданной силе F2 и крайним значениям инерционного зазора δ вычисляют по формуле (2) значение силы F3.
4. По значению F3, пользуясь табл. 2, предварительно определяют разряд пружины.
5. По табл. 11-17 находят строку, в которой наружный диаметр витка пружины наиболее близок к предварительно заданному значению D1. В этой же строке находят соответствующие значения силы F3 и диаметра проволоки d.
6. Для пружин из закаливаемых марок сталей максимальное касательное напряжение τ3 находят по табл. 2, для пружин из холоднотянутой и термообработанной τ3 вычисляют с
учетом значений временного сопротивления Rm. Для холоднотянутой проволоки Rm определяют из ГОСТ 9389-75, для термообработанной – из ГОСТ 1071-81.
7. По полученным значениям F3 и τ3, aтакже по заданному значению F2 по формулам (5) и (5а) вычисляют критическую скорость vK и отношение vmax/vK, подтверждающее или
отрицающее принадлежность пружины к предварительно установленному классу.
При несоблюдении условий vmax/vK<1 пружины I и II классов относят к последующему классу или повторяют расчеты, изменив исходные условия. Если невозможно изменение исходных условий, работоспособность обеспечивается комплектом запасных пружин.
8. По окончательно установленному классу и разряду в соответствующей таблице на параметры витков пружин, помимо ранее найденных величин F3, D1, и d, находят величины c1 и s3, после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)… (25).
Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в ред. 1990г.
Пружина сжатия

Пружина растяжения

|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
1. Сила пружины при предварительной деформации, Н |
F1 |
Принимаются в зависимости от нагрузки пружины |
|
2. Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н |
F2 |
|
|
3. Рабочий ход пружины, мм |
h |
|
|
4. Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с |
Vmax |
|
|
5. Выносливость пружины, число циклов до разрушения |
NF |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
6. Наружный диаметр пружины, мм |
D1 |
Предварительно назначают с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
7. Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации |
δ |
δ = 1-F2/F3. (1) Для пружин сжатия классов I и IIδ=0,05…0,25; для пружин растяжения δ=0,05…0,10; для одножильных пружин класса IIIδ=0,10…0,40; для трехжильных класса IIIδ=0,15…0,40 |
|
8. Сила пружины при максимальной деформации, Н |
F3 |
F3=F2/(1-δ) (2) Уточняется по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
9. Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н |
F0 |
F0= (0,1… 0,25) F3 |
|
10. Диаметр проволоки, мм |
d |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86 |
|
11. Диаметр трехжильного троса, мм |
d1 |
|
|
12. Жесткость одного витка пружины, Н/мм |
c1 |
|
|
13. Максимальная деформация одного витка пружины, мм |
s’3 (при F0=0) s»3 (при F0>0) |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86
|
|
14. Максимальное касательное напряжение пружины, Н/мм2 (Коэффициент k см. п. 35) |
τ3 |
Назначается по табл. 2 ГОСТ 13764-86. При проверке
Для трехжильных пружин
|
|
15. Критическая скорость пружины сжатия, м/с (Максимальная скорость подвижного звена механизма vmax должна быть равна или меньше vK, т.е. vK > vmax) |
vк |
Для трехжильных пружин
|
|
16. Модуль сдвига, Н/мм2 |
G |
Для пружинной стали G = 7,85·104 |
|
17. Динамическая (гравитационная) плотность материала, Н·с2/м4 |
Р |
p = γ/g, где g-ускорение свободного падения, м/с2; γ — удельный вес, Н/м3. Для пружиннойстали р = 8·103 |
|
18. Жесткость пружины, Н/мм |
с |
Для пружин с предварительным напряжением
Для трехжильных пружин
|
|
19. Число рабочих витков пружины |
n |
n = c1/c (7) |
|
20. Полное число витков пружины |
n1 |
n1 = n+ n2, (8) где n2 — число опорных витков |
|
21. Средний диаметр пружины, мм |
D |
D = D1 – d = D2 + d Для трехжильных пружин D = D1– d1= D2+ d1(9a) |
|
22. Индекс пружины |
i |
i = D/d (10) Для трехжильных пружин i= D/d1 (10а) Рекомендуется назначать от 4 до 12 |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
||||
|
23. Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки |
Δ |
Для трехжильного троса с углом свивкиβ=24° определяется по таблице, приведенной ниже |
||||
|
i |
40 |
45 |
50 |
55 |
60 |
7,0 и более |
|
Δ |
1,029 |
1,021 |
1,015 |
1,010 |
1,005 |
1,000 |
|
24. Предварительная деформация пружины, мм |
s1 |
s1=F1/c (11) |
||||
|
25. Рабочая деформация пружины, мм |
s2 |
s2= F2/c (12) |
||||
|
26. Максимальная деформация пружины, мм |
s3 |
s3= F3/c (13) |
||||
|
27. Длина пружины при максимальной деформации, мм |
l3 |
l3 = (n1 + 1 – n3)d, (14) где n3 — число обработанных витков. Для трехжильных пружин l3 = (n + l)d1Δ. (14а) Для пружин растяжения с зацепами l3 = l0 + s3 |
||||
|
28. Длина пружины в свободном состоянии, мм |
l0 |
l0=l3+s3 (15) |
||||
|
29. Длина пружины растяжения без зацепов в свободном состоянии, мм |
l0‘ |
l0‘ = (n1+1)d (15а) |
||||
|
30. Длина пружины при предварительной деформации, мм |
1l |
l1 = l0-s1. (16) Для пружин растяжения l1= l0+s1(16а) |
||||
|
31. Длина пружины при рабочей деформации, мм |
l2 |
l2=l0-s2. (17) Для пружин растяжения l2=l0+s2 (17а) |
||||
|
32. Шаг пружины в свободном состоянии, мм |
t |
t = s’3+d. (18) Для трехжильных пружин t = s’3+d1Δ. (18а) Для пружин растяжения t = d(18б) |
||||
|
33. Напряжение в пружине при предварительной деформации, Н/мм2 |
τ1 |
|
||||
|
34. Напряжение в пружине при рабочей деформации, Н/мм2 |
τ2 |
|
||||
|
35. Коэффициент, учитывающий кривизну витка пружины |
k |
Для трехжильных пружин
|
||||
|
36. Длина развернутой пружины (для пружин растяжения без зацепов), мм |
l |
|
||||
|
37. Масса пружины (для пружин растяжения без зацепов), кг |
m |
|
||||
|
38. Объем, занимаемый пружиной (без учета зацепов пружины), мм3 |
V |
|
||||
|
39. Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм |
λ |
Устанавливается в зависимости от формы опорного витка |
||||
|
40. Внутренний диаметр пружины, мм |
D2 |
D2=D1-2d (25) |
||||
|
41. Временное сопротивление проволоки при растяжении, Н/мм2 |
Rm |
Устанавливается при испытаниях проволоки или по ГОСТ 9389-75 и ГОСТ 1071-81 |
||||
|
42. Максимальная энергия, накапливаемая пружиной, или работа деформации, МДж |
|
Для пружин сжатия и растяжения без предварительного напряжения
для пружин растяжения с предварительным напряжением
|
Методика определения размеров пружин по ГОСТ 13765-86.
1. Исходными величинами для определения размеров пружин являются силы F1 и F2, рабочий ход h, наибольшая скорость перемещения подвижного конца пружины при нагружении или при разгрузке vmах, выносливость NF и наружный диаметр пружины D1 (предварительный).
Если задана только одна сила F2, то вместо рабочего хода h для подсчета берут величину рабочей деформации s2, соответствующую заданной силе.
2. По величине заданной выносливости NF предварительно определяют принадлежность пружины к соответствующему классу по табл. 1.
3. По заданной силе F2 и крайним значениям инерционного зазора δ вычисляют по формуле (2) значение силы F3.
4. По значению F3, пользуясь табл. 2, предварительно определяют разряд пружины.
5. По табл. 11-17 находят строку, в которой наружный диаметр витка пружины наиболее близок к предварительно заданному значению D1. В этой же строке находят соответствующие значения силы F3 и диаметра проволоки d.
6. Для пружин из закаливаемых марок сталей максимальное касательное напряжение τ3 находят по табл. 2, для пружин из холоднотянутой и термообработанной τ3 вычисляют с
учетом значений временного сопротивления Rm. Для холоднотянутой проволоки Rm определяют из ГОСТ 9389-75, для термообработанной — из ГОСТ 1071-81.
7. По полученным значениям F3 и τ3, aтакже по заданному значению F2 по формулам (5) и (5а) вычисляют критическую скорость vK и отношение vmax/vK, подтверждающее или
отрицающее принадлежность пружины к предварительно установленному классу.
При несоблюдении условий vmax/vK<1 пружины I и II классов относят к последующему классу или повторяют расчеты, изменив исходные условия. Если невозможно изменение исходных условий, работоспособность обеспечивается комплектом запасных пружин.
8. По окончательно установленному классу и разряду в соответствующей таблице на параметры витков пружин, помимо ранее найденных величин F3, D1, и d, находят величины c1 и s3, после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)… (25).
« Назад [Расчет пружин] Далее »
Средний диаметр витка пружины Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Дизайн машины ↺ | |
| Дизайн машины | Проектирование элементов машин ↺ | |
| Проектирование элементов машин | Конструкция пружин ↺ | |
| Конструкция пружин | Спиральные пружины ↺ |
|
✖Внешний диаметр витка пружины определяется как внешний диаметр витка витка пружины.ⓘ Внешний диаметр витка пружины [Do] |
+10% -10% |
||
|
✖Внутренний диаметр витка пружины определяется как внутренний диаметр витка пружинной обмотки.ⓘ Внутренний диаметр витка пружины [Di] |
+10% -10% |
|
✖Средний диаметр витка пружины определяется как среднее значение внутреннего и внешнего диаметров пружины.ⓘ Средний диаметр витка пружины [D] |
⎘ копия |
Средний диаметр витка пружины Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Внешний диаметр витка пружины: 40 Миллиметр –> 0.04 метр (Проверьте преобразование здесь)
Внутренний диаметр витка пружины: 32 Миллиметр –> 0.032 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.036 метр –>36 Миллиметр (Проверьте преобразование здесь)
14 Спиральные пружины Калькуляторы
Средний диаметр витка пружины формула
Средний диаметр витка пружины = (Внешний диаметр витка пружины+Внутренний диаметр витка пружины)/2
D = (Do+Di)/2
Определить весну?
Пружина – это упругий объект, хранящий механическую энергию. Пружины обычно изготавливаются из пружинной стали. Есть много весенних дизайнов. В повседневном использовании этот термин часто относится к винтовым пружинам. Жесткость или жесткость пружины – это изменение прилагаемой силы, деленное на изменение прогиба пружины.