Столкновение молекулы со стенкой
Пусть
скорость
![]() i
i
молекулы
с номером i
направлена
под произвольным углом к стенке (рис.
4.4). При столкновении проекция скорости
на ось X
vix
меняет
знак, а проекции скорости на направления,
совпадающие с осями Y
и
Z,
viy
и
viz,
остаются
без изменения. После соударения
![]()
Рис. 4.4
Объясняется
это тем, что при абсолютно упругом ударе
отсутствуют силы, параллельные стенке.
Изменение проекций импульса молекулы
на ось X
равно:
![]()
(4.4.1)
где
т0
—
масса молекулы.
Согласно
закону сохранения импульса стенке
сосуда молекулой будет передан импульс
2m0vix.
Следовательно,
в соответствии со вторым законом Ньютона
на стенку за время удара подействует
импульс силы 2m0vix,
направленный
перпендикулярно стенке.
Число соударений со стенкой молекул, скорости которых близки к VIX
За
время Δt
стенки
могут достичь лишь молекулы со скоростями
vix
> 0,
которые находятся от нее на расстоянии,
не превышающем vixΔt
(рис.
4.5). Эти молекулы движутся слева направо.
Молекулы, находящиеся на больших
расстояниях, не успеют долететь до
стенки*.
*
Заметим, что столкновения
молекул друг с другом не влияют на число
их столкновений со стенкой. Если
какая-либо молекула, у которой vix
> 0, из-за столкновений
не сможет достигнуть стенки, то ее место
займет какая-то другая молекула. Давление
определяется средним числом молекул с
различными скоростями, которое не
меняется в состоянии теплового равновесия
при столкновениях.

Рис. 4.5
Не
надо думать, что значения проекций
скоростей viy
и
viz
как-то
влияют на достижение молекулами стенки
CD.
Если
молекула столкнется со стенкой ВС
или
АВ
(см.
рис. 4.5), то проекция скорости vix
при
этом не изменится и молекула сместится
вдоль оси X
по-прежнему
на отрезок vixΔt
Выделенный
объем CC’DD’
равен
vixΔtS.
Число
молекул в этом объеме со скоростями,
близкими к vix,
составляет
![]()
(4.4.2)
где
ni
—
число молекул со скоростями, близкими
к
vix
> 0, в
1 см3.
Импульс,
переданный
стенке
молекулами
со
скоростями
vix
> 0
Переданный
молекулами (их число равно Δzi)
импульс равен произведению Δzi
на
импульс, переданный одной молекулой
(определяется по формуле (4.4.1)):
![]()
(4.4.3)
Импульс средней силы, действующий на стенку со стороны всех молекул
Молекулы
со скоростями, близкими к vix,
за
время Δt
меняют
импульс стенки на
![]()
Изменение
импульса стенки за время Δt
всеми молекулами, столкнувшимися со
стенкой, равно сумме выражений (4.4.3) по
скоростям vix
> 0
всех молекул:

(4.4.4)
Согласно
второму закону Ньютона импульс силы
FΔt,
действующей
на стенку, равен изменению импульса
стенки:
![]()
(4.4.5)
Выразим
этот импульс силы через средний квадрат
проекции скорости на ось X,
который
согласно формуле (4.3.3) определяется так:

(4.4.6)
где суммирование
осуществляется по всем проекциям
скоростей, как положительным, так и
отрицательным. Но положительные значения
проекций скоростей встречаются столь
же часто, как и отрицательные. Поэтому

или, учитывая определение
среднего квадрата (4.4.6), будем иметь:
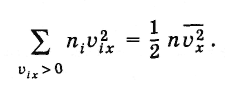
(4.4.7)
Заменяя в уравнении
(4.4.5) сумму по проекциям скоростей ее
выражением (4.4.7), получим средний импульс
силы:
![]()
(4.4.8)
Этот
результат можно пояснить графически.
На рисунке 4.6, а изображена зависимость
от времени силы f,
действующей
на стенку при столкновении с нею различных
молекул. Время соударения δt
‹‹
At.
Сила
меняется хаотически в зависимости от
времени. Площадь под каждым пиком
представляет собой импульс силы,
действующей на стенку со стороны одной
молекулы при соударении. Суммарная
площадь под всеми пиками (ее численное
значение) дает импульс силы, действующей
на стенку за время At.
Средний
импульс силы
![]()
Δt
графически
характеризуется площадью прямоугольника
(рис. 4.6, б),
равной
суммарной площади импульсов сил от
отдельных молекул.

Рис. 4.6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема: Найти импульс молекулы водорода (Прочитано 5737 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Найти импульс молекулы водорода при температуре 20° С. Скорость молекулы считать равной средней квадратичной скорости.

Записан
Решение.
Импульс молекулы водорода определим по формуле:
р = m0∙υ (1).
m0 – масса одной молекулы водорода:
[ {{m}_{0}}=frac{M}{{{N}_{A}}} (2). ]
М – малярная масса молекулы водорода, М = 2∙10-3 кг/моль, NА число Авогадро, NА = 6,02∙1023 моль-1.
Средняя квадратическая скорость определяется по формуле:
[ begin{align}
& {{upsilon }_{K}}=sqrt{frac{3cdot Rcdot T}{M}} (3). \
& p=frac{M}{{{N}_{A}}}cdot sqrt{frac{3cdot Rcdot T}{M}} (4). \
end{align} ]
R = 8,31 Дж/моль∙К, R – универсальная газовая постоянная. Т = 293 К.
р = 634,9∙10-26 кг∙м/с.
« Последнее редактирование: 07 Мая 2015, 06:06 от alsak »

Записан
Меню
- Главная
- Заказ решений
- Готовые решения
- Статьи
- Новости
- Авторы
Есть идеи?
Решения Чертовасайт решений Чертова А.Г. Воробьева А.А.
Поиск
Глава2. Молекулярная физика и термодинамика (§ 8-12) >> §10 Элементы статистической физики >> задача – 10.29
Условие:
Вывести формулу, определяющую среднее значение компонента импульса < р> молекул идеального газа.
При клике на картинку откроется ее увеличенная версия в новой вкладке.
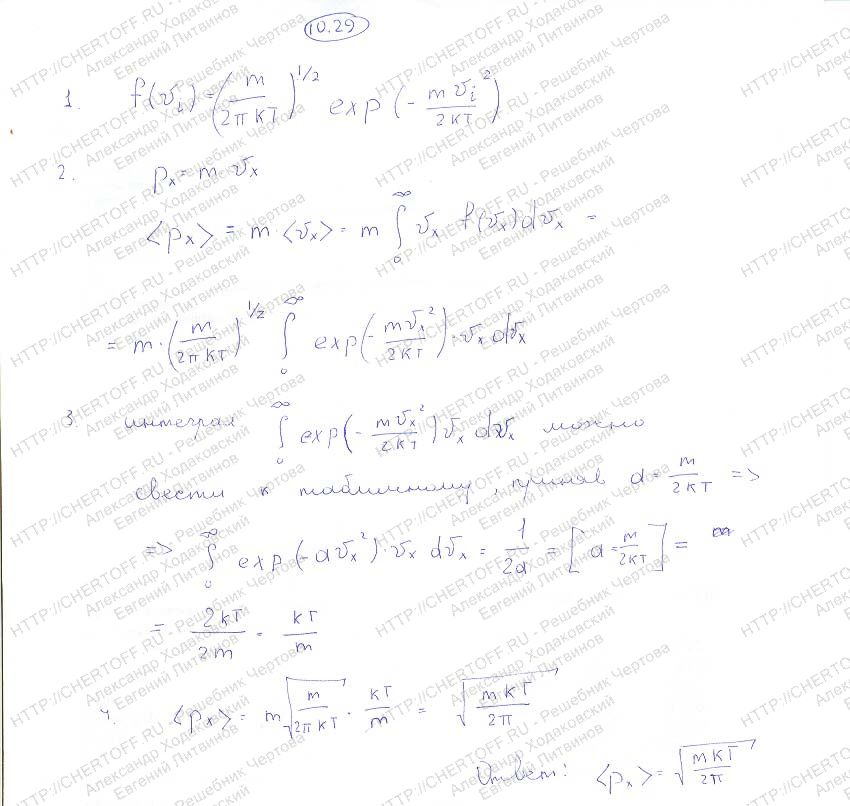
Не забываем поделиться записью!
Последние статьи
- Подходы к решению задач по физике
- Что такое физика и какие задачи и вопросы она решает?
- Общие рекомендации по решению статистических задач
- Он-лаин или офф-лаин обучение? Что выбрать?
- Изучение геометрии в восьмом классе без хлопот становится реальностью
Наши партнеры

© 2012 Решения Чертова | Авторы Bandit & AJ Акции | Sitemap | FAQ&ask
![]()
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5

