Коэффициент
теплопроводности является физическим
параметром вещества и в общем случае
зависит от температуры, давления и рода
вещества. В большинстве случаев
коэффициент теплопроводности для
различных материалов определяется
экспериментально с помощью различных
методов. Большинство из них основано
на измерении теплового потока и градиента
температур в исследуемом веществе.
Коэффициент теплопроводности λ, Вт/(м×К),
при этом определяется из соотношения:
из
которого следует, что коэффициент
теплопроводности численно равен
количеству теплоты, которое проходит
в единицу времени через единицу
изотермической поверхности при
температурном градиенте, равном единице.
Примерные значения коэффициента
теплопроводности различных веществ
показаны на рис.
1.4Так
как тела могут иметь различную температуру,
а при наличии теплообмена и в самом теле
температура будет распределена
неравномерно, т.е. в первую очередь важно
знать зависимость коэффициента
теплопроводности от температуры. Опыты
показывают, что для многих материалов
с достаточной для практики точностью
зависимость коэффициента теплопроводности
от температуры можно принять
линейной:
где
λ0 –
значение коэффициента теплопроводности
при температуре t0;
b – постоянная, определяемая опытным
путём.
Коэффициент
теплопроводности газов. Согласно
кинетической теории перенос теплоты
теплопроводностью в газах при обычных
давлениях и температурах определяется
переносом кинетической энергии
молекулярного движения в результате
хаотического движения и столкновения
отдельных молекул газа. При этом
коэффициент теплопроводности определяется
соотношением:
где –
средняя скорость перемещения молекул
газа; –
средняя длина свободного пробега молекул
газа между соударениями; –
теплоёмкость газа при постоянном
объёме; –
плотность газа. С увеличением давления
в равной мере увеличивается плотность ,
уменьшается длина пробега и
произведение сохраняется
постоянным. Поэтому коэффициент
теплопроводности заметно не меняется
с изменением давления. Исключение
составляют очень малые (меньше 2,66×103Па)
и очень большие (2×109Па)
давления. Средняя скорость перемещения
молекул газа зависит от температуры:
где
Rμ—
универсальная газовая постоянная,
равная 8314,2 Дж/(кмоль×К); μ — молекулярная
масса газа; Т — температура, К. Теплоемкость
газов возрастает с повышением температуры.
Этим объясняется тот факт, что
коэффициент теплопроводности для газов
с повышением температуры возрастает.
Коэффициент теплопроводности λ газов
лежит в пределах от 0,006 до 0,6 Вт/(м×К). На
рис. 1.5 представлены результаты измерений
коэффициента теплопроводности
различных газов, проведенных Н. Б.
Варгафтиком.
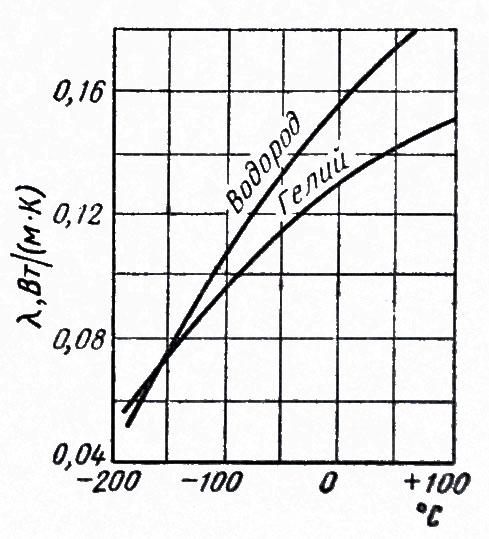
Среди газов резко
выделяются своим коэффициентом
теплопроводности гелий и водород.
Коэффициент теплопроводности у них в
5—10раз больше, чем у других газов. Это
наглядно видно на рис. 1.6. Молекулы гелия
и водорода обладают малой массой, а
следовательно, имеют большую среднюю
скорость перемещения, чем и объясняется
их высокий коэффициент
теплопроводности.
Коэффициенты
теплопроводности водяного пара и других
реальных газов, существенно отличающихся
от идеальных, сильно зависят также от
давления. Для газовых смесей коэффициент
теплопроводности не может быть определён
по закону аддитивности, его нужно
определять опытным путём.
Рис.1.5
Коэффициенты теплопроводности газов.
1-водяной
пар; 2-двуокись углерода; 3-воздух;
4-аргон; 5-кислород; 6-азот.
Рис.
1.6 Коэффициенты теплопроводности гелия
и водорода.
Коэффициент
теплопроводности жидкостей. Механизм
распространения теплоты в капельных
жидкостях можно представить как перенос
энергии путем нестройных упругих
колебаний. Такое теоретическое
представление о механизме передачи
теплоты в жидкостях, выдвинутое А. С.
Предводителевым, было использовано Н.
Б. Варгафтиком для описания опытных
данных по теплопроводности различных
жидкостей. Для большинства жидкостей
теория нашла хорошее подтверждение. На
основании этой теории была получена
формула для коэффициента теплопроводности
следующего вида:
где –
теплоёмкость жидкости при постоянном
давлении; –
плотность жидкости; μ – молекулярная
масса. Коэффициент А, пропорциональный
скорости распространения упругих волн
в жидкости, не зависит от природы
жидкости, но зависит от температуры,
при этом Аср≈const.
Так как плотность ρ жидкости с повышением
температуры убывает, то из уравнения
(1.21) следует, что для жидкостей с постоянной
молекулярной массой (неассоциированные
и слабо ассоциированные жидкости) с
повышением температуры коэффициент
теплопроводности должен уменьшаться.
Для жидкостей, сильно ассоциированных
(вода, спирты и т. д.) в формулу (1.21) нужно
ввести коэффициент ассоциации, учитывающий
изменение молекулярной массы. Коэффициент
ассоциации зависит также от температуры,
и поэтому при различных температурах
он может влиять на коэффициент
теплопроводности по-разному. Опыты
подтверждают, что для большинства
жидкостей с повышением температуры
коэффициент теплопроводности λ убывает,
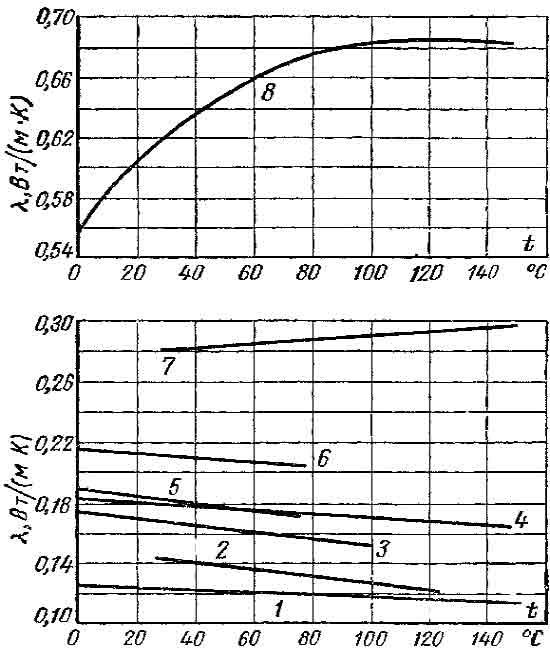
исключение составляют вода и глицерин
(рис. 1.7). Коэффициент теплопроводности
капельных жидкостей лежит примерно в
пределах от 0,07 до 0,7Вт/(м×К). При повышении
давления коэффициенты теплопроводности
жидкостей возрастают.
Рис.
1.7 Коэффициенты теплопроводности
различных жидкостей.
1-вазелиновое
масло; 2-бензол; 3-ацетон; 4-касторовое
масло; 5-спирт этиловый; 6-спирт метиловый;
7-глицерин; 8-вода.
Коэффициент
теплопроводности твердых тел. В
металлах основным передатчиком теплоты
являются свободные электроны, которые
можно уподобить идеальному одноатомному
газу. Передача теплоты при помощи
колебательных движений атомов или в
виде упругих звуковых волн не исключается,
но ее доля незначительна по сравнению
с переносом энергии электронным газом.
Вследствие движения свободных электронов
происходит выравнивание температуры
во всех точках нагревающегося или
охлаждающегося металла. Свободные
электроны движутся как из областей,
более нагретых, в области, менее нагретые,
так и в обратном направлении. В первом
случае они отдают энергию атомам, во
втором отбирают ее. Так как в металлах
носителем тепловой энергии являются
электроны, то коэффициенты тепло- и
электропроводности пропорциональны
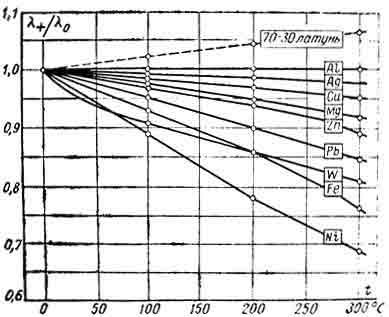
друг другу. При повышении температуры
вследствие усиления тепловых
неоднородностей рассеивание электронов
увеличивается. Это влечет за собой
уменьшение коэффициентов тепло- и
электропроводности чистых металлов
(рис. 1.8). При наличии разного рода примесей
коэффициент теплопроводности металлов
резко убывает. Последнее можно объяснить
увеличением структурных неоднородностей,
которое приводит к рассеиванию электронов.
Так, например, для чистой меди λ=
396Вт/(м×К), для той же меди со следами
мышьяка λ= 142Bт/(м×K).
В отличие от чистых
металлов коэффициенты теплопроводности
сплавов при повышении температуры
увеличиваются (рис. 1.9).
В диэлектриках
с повышением температуры коэффициент
теплопроводности обычно увеличивается
(рис. 1.10). Как правило, для материалов с
большей плотностью коэффициент
теплопроводности имеет более высокое
значение. Он зависит от структуры
материала, его пористости и влажности.
Рис.
1.8 Зависимость
коэффициента теплопроводности от
температуры для некоторых чистых
металлов.
Многие
строительные и теплоизоляционные
материалы имеют пористое строение
(кирпич, бетон, асбест, шлак и др.), и
применение закона Фурье к таким телам
является в известной мере условным.
Наличие пор в материале не позволяет
рассматривать такие тела как сплошную
среду.
Условным является также
коэффициент теплопроводности пористого
материала. Эта величина имеет смысл
коэффициента теплопроводности некоторого
однородного тела, через которое при
одинаковых форме, размерах и температурах
на границах проходит то же количество
теплоты, что и через данное пористое
тело.
Коэффициент теплопроводности
порошкообразных и пористых тел сильно
зависит от их плотности. Например, при
возрастании плотности ρ от 400 до 800
кг/м3 коэффициент
теплопроводности асбеста увеличивается
от 0,105 до 0,248 Вт/(м×К). Такое влияние
плотности ρ на коэффициент теплопроводности
объясняется тем, что теплопроводность
заполняющего поры воздуха значительно
меньше, чем твердых компонентов пористого
материала.
Эффективный коэффициент
теплопроводности пористых материалов
сильно зависит также от влажности. Для
влажного материала коэффициент
теплопроводности значительно больше,
чем для сухого и воды в отдельности.
Например, для сухого кирпича λ= 0,35, для
воды λ = 0,60, а для влажного кирпича λ≈1,0
Вт/(м×К). Этот эффект может быть объяснен
конвективным переносом теплоты,
возникающим благодаря капиллярному
движению воды внутри пористого материала,
и частично тем, что абсорбционно связанная
влага имеет другие характеристики по
сравнению со свободной водой.
Увеличение
коэффициента теплопроводности зернистых
материалов с изменением температуры
можно объяснить тем, что с повышением
температуры возрастает теплопроводность
среды, заполняющей промежутки между
зернами, а также увеличивается
теплопередача излучением зернистого
массива.
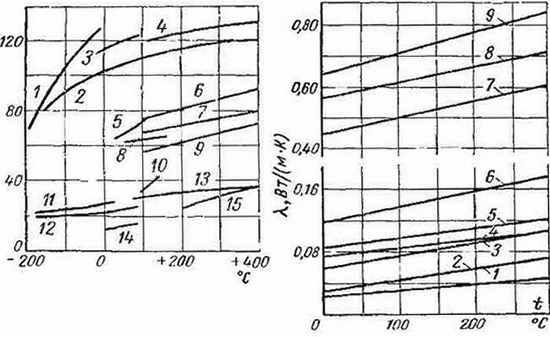
Коэффициенты теплопроводности
строительных и теплоизоляционных
материалов имеют значения, лежащие
примерно в пределах от 0,023 до 2,9Bт/(м×K).
Материалы с низким значением коэффициента
теплопроводности [меньше 0,25Вт/(м×К)],
обычно применяемые для тепловой изоляции,
называются теплоизоляционными.
|
Рис. 1.9 Коэффициенты теплопроводности |
Рис. 1.10 Коэффициенты теплопроводности |
|
1 |
1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 октября 2022 года; проверки требуют 7 правок.
Теплопрово́дность — способность материальных тел проводить тепловую энергию от более нагретых частей тела к менее нагретым частям тела путём хаотического движения частиц тела (атомов, молекул, электронов и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.
Различают стационарный и нестационарный процессы теплопроводности в твердом теле. Стационарный процесс характеризуется неизменными во времени параметрами процесса. Такой процесс устанавливается при длительном поддержании температур теплообменивающихся сред на одном и том же уровне. Нестационарный процесс представляет собой неустановившийся тепловой процесс в телах и средах, характеризуемый изменением температуры в пространстве и во времени.
Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости.
Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В Международной системе единиц (СИ) единицей измерения коэффициента теплопроводности является Вт/(м·K).
Исторически считалось, что передача тепловой энергии связана с перетеканием гипотетического теплорода от одного тела к другому. Однако с развитием молекулярно-кинетической теории явление теплопроводности получило своё объяснение на основе взаимодействия частиц вещества. Молекулы в более нагретых частях тела движутся быстрее и передают энергию посредством столкновений медленным частицам в более холодных частях тела.
Закон теплопроводности Фурье[править | править код]
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
где 



В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
где 



Связь с электропроводностью[править | править код]
Связь коэффициента теплопроводности 

- где
— постоянная Больцмана,
— заряд электрона,
— абсолютная температура.
Коэффициент теплопроводности газов[править | править код]
В газах коэффициент теплопроводности может быть найден по приближённой формуле[2]
где 



где 







Теплопроводность в сильно разреженных газах[править | править код]
Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): 


Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Обобщения закона Фурье[править | править код]
Закон Фурье не учитывает инерционность процесса теплопроводности, то есть в этой модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье неприменим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. п. Инерционность в уравнения переноса первым ввел Максвелл[4], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[5]
Если время релаксации 
Коэффициент теплопроводности[править | править код]
Коэффициент теплопроводности в 1 Вт/м·К означает, что 1 квадратный метр вещества передаёт за 1 секунду 1 джоуль энергии на расстояние в 1 метр вследствие разницы температур в 1 кельвин.
или
Коэффициент теплопроводности в 1 Вт/м·К означает, что 1 квадратный метр вещества передаёт энергию на расстояние в 1 метр со скоростью 1 ватт вследствие разницы температур в 1 кельвин.
Коэффициенты теплопроводности различных веществ[править | править код]
| Материал | Теплопроводность, Вт/(м·K) |
|---|---|
| Графен | 4840 ± 440 — 5300 ± 480 |
| Алмаз | 1001—2600 |
| Графит | 278,4—2435 |
| Арсенид бора[en] | 200—2000 |
| Карбид кремния | 490 |
| Серебро | 430 |
| Медь | 401 |
| Оксид бериллия | 370 |
| Золото | 320 |
| Алюминий | 202—236 |
| Нитрид алюминия | 200 |
| Нитрид бора | 180 |
| Кремний | 150 |
| Латунь | 97—111 |
| Хром | 107 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Оксид цинка | 54 |
| Сталь нелегированная | 47—58 |
| Свинец | 35,3 |
| Титан | 21,9 |
| Сталь нержавеющая (аустенитная)[6] | 15 |
| Кварц | 8 |
| Термопасты высокого качества | 5—12 (на основе соединений углерода) |
| Гранит | 2,4 |
| Бетон сплошной | 1,75 |
| Бетон на гравии или щебне из природного камня | 1,51 |
| Базальт | 1,3 |
| Стекло | 1—1,15 |
| Термопаста КПТ-8 | 0,7 |
| Бетон на песке | 0,7 |
| Вода при нормальных условиях | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Силиконовое масло | 0,16 |
| Пенобетон | 0,05—0,3 |
| Газобетон | 0,1—0,3 |
| Древесина | 0,15 |
| Нефтяные масла | 0,12 |
| Свежий снег | 0,10—0,15 |
| Пенополистирол (горючесть Г1) | 0,038—0,052 |
| Экструдированный пенополистирол (горючесть Г3 и Г4) | 0,029—0,032 |
| Стекловата | 0,032—0,041 |
| Каменная вата | 0,034—0,039 |
| Пенополиизоцианурат (PIR) | 0,023 |
| Пенополиуретан (поролон) | 0,029-0,041 |
| Воздух (300 K, 100 кПа) | 0,022 |
| Аэрогель | 0,017 |
| Диоксид углерода (273—320 K, 100 кПа) | 0,017 |
| Аргон (240—273 K, 100 кПа) | 0,015 |
| Вакуум (абсолютный) | 0 (строго) |
Также нужно учитывать передачу тепла из-за конвекции молекул и излучения. Например, при полной нетеплопроводности вакуума, тепловая энергия передаётся излучением (Солнце, инфракрасные теплогенераторы). В газах и жидкостях происходит перемешивание разнотемпературных слоёв естественным путём или искусственно (примеры принудительного перемешивания — фены, естественного — электрочайники). Также в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепловой энергии, даже если зазоры представляют собой идеальный вакуум.
Примечания[править | править код]
- ↑ Фурье закон // Естествознание. Энциклопедический словарь.
- ↑ Д.В. Сивухин. Общий курс физики: термодинамика и молекулярная физика. — М.: Физматлит, 2006. — С. 345.
- ↑ Исследование теплопроводности газов. (недоступная ссылка) // Методические указания.
- ↑ J. C. Maxwell, Philos. Trans. Roy. Soc. London 157 (1867) 49.
- ↑ C. Cattaneo, Atti Seminario Univ. Modena 3 (1948) 33.
- ↑ Merkblatt 821 Архивная копия от 8 августа 2014 на Wayback Machine (PDF; 614 kB); Сталь нержавеющая, свойства стали (нем.), таблица 9
См. также[править | править код]
- Теплопередача
- Конвекция
- Равновесный градиент температуры
- Тепловое излучение
- Закон Ньютона — Рихмана
- Уравнение диффузии
- Теплоизоляция
Ссылки[править | править код]
- Теплопроводность воды и водяного пара
- Коэффициенты теплопроводности элементов
- Таблица теплопроводности веществ и материалов
Среднее значение – коэффициент – теплопроводность
Cтраница 1
Среднее значение коэффициентов теплопроводности определяется по графику А А ( /), построенному по опытным данным по изобарам.
[1]
Средние значения коэффициентов теплопроводности Я в зависимости от средней температуры в слое стены ст могут быть определены по рис. III-8.
[3]
А, – среднее значение коэффициента теплопроводности газа, Т – температура, х – расстояние по нормали к волне, индексы 0 и оо относятся к величинам перед и за волной.
[4]
В табл. 3.20 приведены средние значения коэффициента теплопроводности некоторых из наиболее употребительных в криогенной технике материалов для часто встречающихся пар температур.
[6]
На рис. 4 приведены средние значения коэффициентов теплопроводности конструктивно-теплоизоляционных легких бетонов в сухом состоянии, плотного строения и постоянного зернового состава.
[8]
При расчетах можно пользоваться средним значением коэффициента теплопроводности, что упрощает вычисление.
[9]
В технических расчетах обычно принимают средние значения коэффициента теплопроводности, считая его во время процесса теплопередачи постоянным.
[11]
При обобщении опытных данных по изложенному методу приходится пользоваться средними значениями коэффициентов теплопроводности Я и Ядз, что не очень удобно.
[12]
Таким образом, формулы (1.3), (1.6) и (1.7), рекомендуемые Бурш-теином для определения средних значений коэффициентов теплопроводности и удельного электрического сопротивления полупроводникового материала ветвей термоэлемента, соответствуют его работе в режиме холостого хода, а погрешность расчета с использованием этих значений при протекании по термоэлементу электрического тока пренебрежимо мала.
[13]
Здесь выбрана система координат, в которой пламя покоится, х – координата по нормали к фронту пламени, К – среднее значение коэффициента теплопроводности, cv – – средняя теплоемкость при постоянном давлении, т – поток массы через единицу площади в направлении ж, со – скорость химической реакции ( масса горючего, испытывающего превращение в единице объема за единицу времени), д – теплота реакции ( при постоянном давлении), отнесенная к единице массы израсходованного горючего, L – тепловые потери из единицы объема за секунду, связанные с излучением или теплоотводом к стенкам.
[14]
Если U – const и U – const, то, как показано в [17], в скользящем режиме распределение тепла в слое зависит только от интегральных характеристик процесса: интегральной скорости, интегральной положительной скорости, интегральной отрицательной скорости, среднего значения коэффициента теплопроводности К и среднего значения скорости химической реакции. Для случая, когда времена подачи газовой смеси в положительном и отрицательном направлениях одинаковы, удалось детально проанализировать стационарную задачу при протекании одной реакции.
[15]
Страницы:
1
2
Ведущие тенденции современного строительства – это возведение домов с максимальной энергоэффективностью. То есть с возможностью создания и поддержания комфортных условий проживания при минимальных затратах энергоносителей. Понятно, что многим нашим строителям, ведущим возведение своих жилых владений самостоятельно, до таких показателей пока далековато, но стремиться к этому – необходимо всегда.
Прежде всего, это касается минимизации тепловых потерь через строительные конструкции. Достигается такое снижение эффективной термоизоляцией, выполненной на основании теплотехнических расчетов. Проектирование в идеале должны проводить специалисты, но часто обстоятельства понуждают владельцев жилья и такие вопросы брать в свои руки. Значит, необходимо иметь общие представления о базовых понятиях строительной теплотехники. Прежде всего – что такое теплопроводность строительных материалов, в чем она измеряется, как просчитывается.
Если разобраться с этими «азами», то будет проще всерьез, со знанием дела , а не по наитию, заниматься вопросами утепления своего жилья.
Что такое теплопроводность, какими единицами измерения она описывается?
Если не рассматривать каких-то теоретических условий, то в реальности все физические тела, жидкости или газы обладают способностью к передаче тепла. Иными словами, чтобы было понятнее, если какой-то объект начинают нагревать с одной из сторон, он становится проводником тепла, нагреваясь сам и передавая тепловую энергию дальше. Точно так же – и при охлаждении, только с «обратным знаком».
Даже на простом бытовом уровне всем понятно, что эта способность выражена у разных материалов в очень отличающейся степени. Например, одно дело мешать готовящееся на плите кипящее блюдо деревянной лопаткой, и совсем другое – металлической ложкой, которая практически моментально разогреется до такой температуры, что ее невозможно будет держать в руках. Этот пример наглядно показывает, что теплопроводность металла во много раз выше, чем у дерева.
И таких примеров – масса, буквально на каждом шагу. Например, прикоснитесь рукой к обычной деревянной двери в комнате, и к металлической ручке, прикрученной на ней. По ощущениям – ручка холоднее. Но такого не может быть – все предметы в помещении имеют примерно равную температуру. Просто металл ручки быстрее отвел на себя тепло тела, что и вызвало ощущения более холодной поверхности.
Коэффициент теплопроводности материала
Мнение эксперта:
Афанасьев Е.В.
Главный редактор проекта Stroyday.ru.
Инженер.
Задать вопрос эксперту
Существует специальная единица, которая характеризует любой материал, как проводник тепла. Называется она коэффициентом теплопроводности, обозначается обычно греческой буквой λ, и измеряется в Вт/(м×℃). (Во многих встречающихся формулах вместо градусов Цельсия ℃ указаны градусы Кельвина, К, но сути это не меняет).
Этот коэффициент показывает способность материала передавать определенное количество тепла на определённое расстояние за единицу времени. Причем, это показатель характеризует именно материал, то есть без привязки к каким бы то ни было размерам.
Такие коэффициенты рассчитаны для практически любых строительных и иных материалов. Ниже в данной публикации приведены таблицы для различных групп – растворов, бетонов, кирпичной и каменной кладки, утеплителей, древесины, металлов и т.д. Даже беглого взгляда на них достаточно, чтобы убедиться, насколько эти коэффициенты могут отличаться.
Очень часто производители стройматериалов того или иного предназначения в череде паспортных характеристик указывают и коэффициент теплопроводности.
Материалы, которые отличаются высокой проводимостью тепла, например, металлы, как раз и находят часто применение в роли теплоотводов или теплообменников. Классический пример – радиаторы отопления, в которых чем лучше их стенки будут передавать нагрев от теплоносителя, тем эффективнее их работа.
А вот для большинства строительных материалов – ситуация обратная. То есть чем меньше коэффициент теплопроводности материала, из которого возведена условная стенка, тем меньше тепла будет терять здание с приходом холодов. Или, тем меньше можно будет сделать толщину стены при одинаковых показателях теплопроводности.
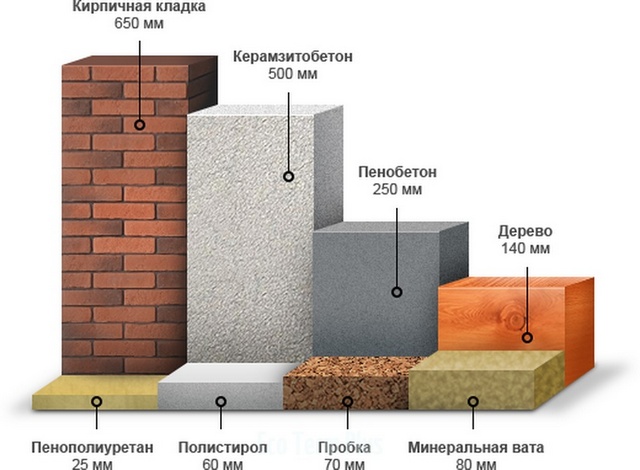
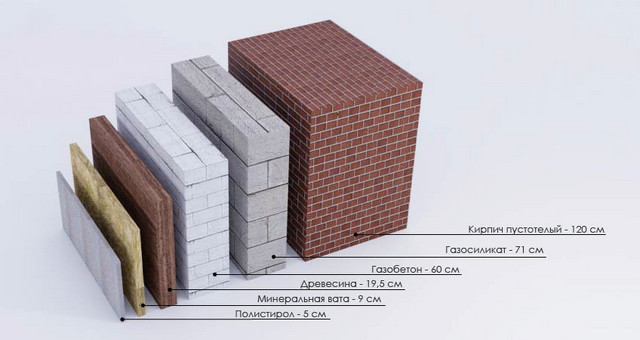
И на титульной картинке к статье, и на иллюстрации ниже показаны весьма наглядные схемы, как будет различаться толщина стены из разных материалов при равных способностях удержать тепло в доме. Комментарии, наверное, не нужны.
В справочной литературе часто указывается не одно значение коэффициента теплопроводности для какого-то материала, а целых три. (А иногда – и больше, так как этот коэффициент может меняться с изменением температуры). И это – правильно, так как на теплопроводные качества влияют и условия эксплуатации. И в первую очередь – влажность.
Это свойственно большинству материалов – при насыщении влагой коэффициент теплопроводности увеличивается. И если ставится цель выполнить расчеты максимально точно, с привязкой к реальным условиям эксплуатации, то рекомендуется не пренебрегать этой разницей.
Итак, коэффициент может даваться расчетный, то есть для совершенно сухого материала и лабораторных условий. Но для реальных расчетов берут его или для режима эксплуатации А, или для режима Б.
Эти режимы складываются консолидировано из климатических особенностей региона и из особенностей эксплуатации конкретного здания (помещения).
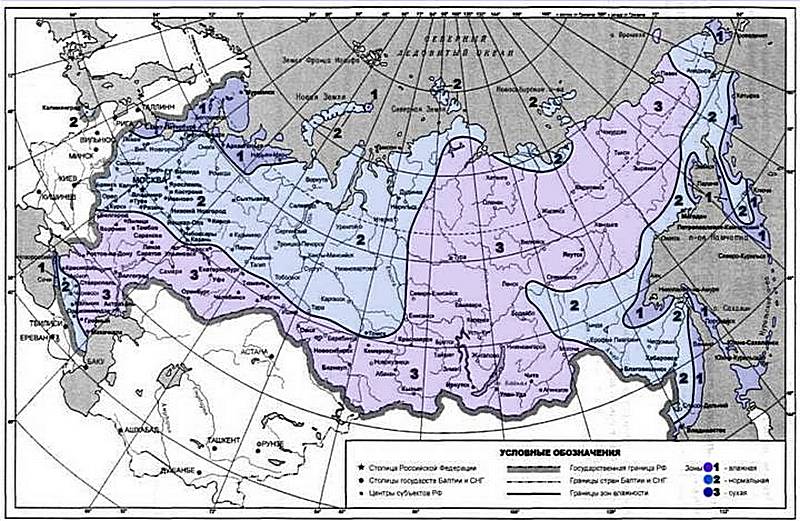
Тип своей климатической зоны по уровню влажности можно определить по предлагаемой карте-схеме:
Особенности влажностного режима помещений определяются по следующей таблице:
Таблица определения влажностного режима помещений
| Влажностной режим помещения | Относительная влажность внутреннего воздуха при температуре: | ||
|---|---|---|---|
| до 12°С | от 13 до 24°С | 25°С и выше | |
| Сухой | до 60% | до 50% | до 40% |
| Нормальный | от 61 до 75% | от 51 до 60% | от 41 до 50% |
| Влажный | 76% и более | от 61 до 75% | от 51 до 60% |
| Мокрый | – | 76% и более | 61% и более |
Кстати, о влажности!..
А хорошо ли вы представляете себе, что такое относительная влажность воздуха. И какой она должна быть в помещениях для поддержания комфортного микроклимата? Если с этим ясности нет – добро пожаловать к специальной публикации нашего портала, посвященной приборам измерения относительной влажности.
Итак, имея данные карты-схемы и таблицы, можно по второй таблице определиться с выбором режима А или Б, от которого будет зависеть реальная величина коэффициента теплопроводности.
Таблица для выбора режима эксплуатации ограждающих конструкций
| Влажностной режим помещения (по таблице) | Зоны влажности (в соотвествии с картой-схемой) | ||
|---|---|---|---|
| 3 – сухая | 2 – нормальная | 1 – влажная | |
| Сухой | А | А | Б |
| Нормальный | А | Б | Б |
| Влажный или мокрый | Б | Б | Б |
Вот по этому режиму и выбирается из табличных данных наиболее близкий к реальности коэффициент теплопроводности.
Таблицы будут приведены ниже, под теоретической частью.
Сопротивление теплопередаче
Мнение эксперта:
Афанасьев Е.В.
Главный редактор проекта Stroyday.ru.
Инженер.
Задать вопрос эксперту
Итак, коэффициент теплопроводности характеризует сам материал. Но с практической точки зрения, наверное, важнее иметь какую-то величину, которая будет описывать теплопроводные способности конкретной конструкции. То есть уже с учетом особенностей ее строения и размеров.
Такая единица измерения есть, и называется она сопротивлением теплопередаче. Ее можно считать обратной величиной коэффициенту теплопроводности, с одновременным учетом толщины материала.
Обозначается сопротивление теплопередаче (или, как его часто именуют, термическое сопротивление) латинской буквой R. Если «плясать» от коэффициента теплопроводности, то определяется оно по следующей формуле.
R = h/λ
где:
R — сопротивление теплопередаче однослойной однородной ограждающей конструкции, м²×℃/Вт;
h — толщина этого слоя, выраженная в метрах;
λ — коэффициент теплопроводности материала, из которого изготовлена эта ограждающая конструкция, Вт/(м×℃).
Очень часто в строительстве используются многослойные конструкции. В том числе одним из слоев нередко выступает утеплительный материал с очень низким коэффициентом теплопроводности – специально, чтобы максимально повысить значение термического сопротивления. Дело в том, что общее значение суммируется из сопротивлений всех слоев, составляющих ограждающую конструкцию. И к ним добавляется сопротивление приграничных слоев воздуха на внешней и внутренней поверхностях конструкции.
Формула сопротивления перегородки с n-слоев будет такой:
Rsum = R₁ + R₂ + …+Rn + Rai + Rao
где:
Rsum— суммарное термическое сопротивление ограждающей конструкции;
R₁ … Rn— сопротивления слоев, от 1 до n;
Rai— сопротивление пристенного слоя воздуха внутри;
Rao— сопротивление пристенного слоя воздуха снаружи.
Для каждого из слоев сопротивление рассчитывается отдельно, исходя из коэффициента теплопроводности материала и толщины.
Есть специальная методика расчета и коэффициентов воздушных прослоек вдоль стены снаружи и внутри. Но для упрощенных расчётов их вполне можно взять равными суммарно 0,16 м²×℃/Вт – большой погрешности не будет.
Кстати, если в конструкции перегородки предусмотрена воздушная полость, не сообщающаяся с внешним воздухом, то она тоже дает весомую добавку к общему сопротивлению теплопередаче. Значения сопротивления теплопередаче воздушных изолированных прослоек показаны в таблице ниже:
Таблица термических сопротивлений замкнутых воздушных прослоек
| Толщина воздушной прослойки, в метрах | В и Г ▲ | Г▼ | ||
|---|---|---|---|---|
| tв > 0 ℃ | tв < 0 ℃ | tв > 0 ℃ | tв < 0 ℃ | |
| 0.01 | 0.13 | 0.15 | 0.14 | 0.15 |
| 0.02 | 0.14 | 0.15 | 0.15 | 0.19 |
| 0.03 | 0.14 | 0.16 | 0.16 | 0.21 |
| 0.05 | 0.14 | 0.17 | 0.17 | 0.22 |
| 0.1 | 0.15 | 0.18 | 0.18 | 0.23 |
| 0.15 | 0.15 | 0.18 | 0.19 | 0.24 |
| 0,2-0,3 | 0.15 | 0.19 | 0.19 | 0.24 |
| Примечания: | ||||
| В и Г ▲ – воздушная прослойка вертикальная, или горизонтальная, с рапространением тепла снизу вверх | ||||
| Г▼ – воздушная прослойка горизонтальная при распространении тепла сверху вниз | ||||
| tв > 0 ℃ – положительная температура воздуха в прослойке | ||||
| tв < 0 ℃ – отрицательная температура воздуха в прослойке | ||||
| Если любая из поверхностей воздушной прослойки, или обе одновременно, оклеены алюминиесвой фольгой, то значение сопротивления теплопередаче принимают вдвое большим. |
Таблицы коэффициентов теплопроводности различных групп строительных материалов
Таблица коэффициентов теплопроводности кирпичных кладок и каменных облицовок стен
| Наименование материала | ρ Средняя плотность материала кг/м³ |
λ₀ Коэффициент теплопроводности в идеальных условиях и в сухом состоянии Вт/(м×℃) |
λА Коэффициент теплопроводности для условий эксплуатации А Вт/(м×℃) |
λБ Коэффициент теплопроводности для условий эксплуатации Б Вт/(м×℃) |
|---|---|---|---|---|
| Кирпичная кладка из сплошного кирпича на различных растворах | ||||
| Стандартный керамический (глиняный) – на цементно-песчаном кладочном растворе | 1800 | 0,56 | 0,70 | 0,81 |
| Стандартный керамический на цементно-шлаковом растворе | 1700 | 0,52 | 0,64 | 0,76 |
| Стандартный керамический на цементно-перлитовом растворе | 1600 | 0,47 | 0,58 | 0,70 |
| Силикатный на цементно-песчаном кладочном растворе | 1800 | 0,70 | 0,76 | 0,87 |
| Трепельный термооизоляционный, на цементно-песчаном кладочном растворе | 1200 | 0,35 | 0,47 | 0,52 |
| – то же, но с плотностью | 1000 | 0,29 | 0,41 | 0,47 |
| Шлаковый, на цементно-песчаном кладочном растворе | 1500 | 0,52 | 0,64 | 0,70 |
| Кладка из пустотного кирпича | ||||
| Кирпич керамический, с плотностью 1400 кг/м³, на цементно-песчаном кладочном растворе | 1600 | 0,47 | 0,58 | 0,64 |
| – то же, но с плотностью кирпича 1300 кг/м³ | 1400 | 0,41 | 0,52 | 0,58 |
| – то же, но с плотностью кирпича 1000 кг/м³ | 1200 | 0,35 | 0,47 | 0,52 |
| Кирпич силикатный, одиннадцатипустотный, на цементно-песчаном кладочном растворе | 1500 | 0,64 | 0,70 | 0,81 |
| – то же, четырнадцатипустотный | 1400 | 0,52 | 0,64 | 0,76 |
| Кладка или облицовка поверхностей натуральным камнем | ||||
| Гранит или базальт | 2800 | 3,49 | 3,49 | 3,49 |
| Мрамор | 2800 | 2,91 | 2,91 | 2,91 |
| Туф | 2000 | 0,76 | 0,93 | 1,05 |
| – то же, но с плотностью | 1800 | 0,56 | 0,70 | 0,81 |
| – то же, но с плотностью | 1600 | 0,41 | 0,52 | 0,64 |
| – то же, но с плотностью | 1400 | 0,33 | 0,43 | 0,52 |
| – то же, но с плотностью | 1200 | 0,27 | 0,35 | 0,41 |
| – то же, но с плотностью | 1000 | 0,21 | 0,24 | 0,29 |
| Известняк | 2000 | 0,93 | 1,16 | 1,28 |
| – то же, но с плотностью | 1800 | 0,70 | 0,93 | 1,05 |
| – то же, но с плотностью | 1600 | 0,58 | 0,73 | 0,81 |
| – то же, но с плотностью | 1400 | 0,49 | 0,56 | 0,58 |
Таблица коэффициентов теплопроводности бетонов различного типа
| Наименование материала | ρ кг/м³ |
λ₀ Вт/(м×℃) |
λА Вт/(м×℃) |
λБ Вт/(м×℃) |
|---|---|---|---|---|
| Бетоны на плотном заполнителе | ||||
| Железобетон | 2500 | 1.69 | 1.92 | 2.04 |
| Бетон на натуральном гравии или щебне | 2400 | 1.51 | 1.74 | 1.86 |
| Бетоны на натуральных пористых заполнителях | ||||
| Пемзобетон | 1600 | 0.52 | 0.6 | 0.68 |
| – то же, но с плотностью | 1400 | 0.42 | 0.49 | 0.54 |
| – то же, но с плотностью | 1200 | 0.34 | 0.4 | 0.43 |
| – то же, но с плотностью | 1000 | 0.26 | 0.3 | 0.34 |
| – то же, но с плотностью | 800 | 0.19 | 0.22 | 0.26 |
| Туфобетон | 1800 | 0.64 | 0.87 | 0.99 |
| – то же, но с плотностью | 1600 | 0.52 | 0.7 | 0.81 |
| – то же, но с плотностью | 1400 | 0.41 | 0.52 | 0.58 |
| – то же, но с плотностью | 1200 | 0.29 | 0.41 | 0.47 |
| Бетон на вулканическом шлаке | 1600 | 0.52 | 0.64 | 0.7 |
| – то же, но с плотностью | 1400 | 0.41 | 0.52 | 0.58 |
| – то же, но с плотностью | 1200 | 0.33 | 0.41 | 0.47 |
| – то же, но с плотностью | 1000 | 0.24 | 0.29 | 0.35 |
| – то же, но с плотностью | 800 | 20 | 0.23 | 0.29 |
| Бетоны на искусственных пористых наполнителях | ||||
| Керамзитобетон на кварцевом песке с поризацией | 1200 | 0.41 | 0.52 | 0.58 |
| – то же, но с плотностью | 1000 | 0.33 | 0.41 | 0.47 |
| – то же, но с плотностью | 800 | 0.23 | 0.29 | 0.35 |
| Керамзитобетон на керамзитовом песке или керамзитопенобетон | 1800 | 66 | 0.8 | 0.92 |
| – то же, но с плотностью | 1600 | 0.58 | 0.67 | 0.79 |
| – то же, но с плотностью | 1400 | 0.47 | 0.56 | 0.65 |
| – то же, но с плотностью | 1200 | 0.36 | 0.44 | 0.52 |
| – то же, но с плотностью | 1000 | 0.27 | 0.33 | 0.41 |
| – то же, но с плотностью | 800 | 0.21 | 0.24 | 0.31 |
| – то же, но с плотностью | 600 | 0.16 | 0.2 | 0.26 |
| – то же, но с плотностью | 500 | 0.14 | 0.17 | 0.23 |
| Керамзитобетон на перлитовом песке | 1000 | 0.28 | 0.35 | 0.41 |
| – то же, но с плотностью | 800 | 0.22 | 0.29 | 0.35 |
| Перлитобетон | 1200 | 0.29 | 0.44 | 0.5 |
| – то же, но с плотностью | 1000 | 0.22 | 0.33 | 0.38 |
| – то же, но с плотностью | 800 | 0.16 | 0.27 | 0.33 |
| – то же, но с плотностью | 600 | 0.12 | 0.19 | 0.23 |
| Шлакопемзобетон | 1800 | 0.52 | 0.63 | 0.76 |
| – то же, но с плотностью | 1600 | 0.41 | 0.52 | 0.63 |
| – то же, но с плотностью | 1400 | 0.35 | 0.44 | 0.52 |
| – то же, но с плотностью | 1200 | 0.29 | 0.37 | 0.44 |
| – то же, но с плотностью | 1000 | 0.23 | 0.31 | 0.37 |
| Шлакопемзопено и шлакопемзогазобетон | 1600 | 0.47 | 0.63 | 0.7 |
| – то же, но с плотностью | 1400 | 0.35 | 0.52 | 0.58 |
| – то же, но с плотностью | 1200 | 0.29 | 0.41 | 0.47 |
| – то же, но с плотностью | 1000 | 0.23 | 0.35 | 0.41 |
| – то же, но с плотностью | 800 | 0.17 | 0.29 | 0.35 |
| Вермикулетобетон | 800 | 0.21 | 0.23 | 0.26 |
| – то же, но с плотностью | 600 | 0.14 | 0.16 | 0.17 |
| – то же, но с плотностью | 400 | 0.09 | 0.11 | 0.13 |
| – то же, но с плотностью | 300 | 0.08 | 0.09 | 0.11 |
| Ячеистые бетоны | ||||
| Газобетон, пенобетон, газосиликат, пеносиликат | 1000 | 0.29 | 0.41 | 0.47 |
| – то же, но с плотностью | 800 | 0.21 | 0.33 | 0.37 |
| – то же, но с плотностью | 600 | 0.14 | 0.22 | 0.26 |
| – то же, но с плотностью | 400 | 0.11 | 0.14 | 0.15 |
| – то же, но с плотностью | 300 | 0.08 | 0.11 | 0.13 |
| Газозолобетон, пенозолобетон | 1200 | 0.29 | 0.52 | 0.58 |
| – то же, но с плотностью | 1000 | 0.23 | 0.44 | 0.59 |
| – то же, но с плотностью | 800 | 0.17 | 0.35 | 0.41 |
Таблица коэффициентов теплопроводности строительных растворов на цементной, известковой, гипсовой основе
| Наименование материала | ρ кг/м³ |
λ₀ Вт/(м×℃) |
λА Вт/(м×℃) |
λБ Вт/(м×℃) |
|---|---|---|---|---|
| Обычный цементно-песчаный раствор | 1800 | 0.58 | 0.76 | 0.93 |
| Сложный раствор из цемента, песка, извести | 1700 | 0.52 | 0.7 | 0.87 |
| Цементно-шлаковый раствор | 1400 | 0.41 | 0.52 | 0.64 |
| Цементно-перлитовый раствор | 1000 | 0.21 | 0.26 | 0.3 |
| – то же, но с плотностью | 800 | 0.16 | 0.21 | 0.26 |
| Известково-песчаный раствор | 1600 | 0.47 | 0.7 | 0.81 |
| – то же, но с плотностью | 1200 | 0.35 | 0.47 | 0.58 |
| Гипсово-перлитовый раствор | 600 | 0.14 | 0.19 | 0.23 |
| Гипсово-перлитовый поризованный раствор | 500 | 0.12 | 0.15 | 0.19 |
| – то же, но с плотностью | 400 | 0.09 | 0.13 | 0.15 |
| Гипсовые плиты литые конструкционные | 1200 | 0.35 | 0.41 | 0.47 |
| – то же, но с плотностью | 1000 | 0.23 | 0.29 | 0.35 |
| Листы гипсокартона (сухая штукатурка) | 800 | 0.15 | 0.19 | 0.21 |
Таблица коэффициентов теплопроводности дерева, изделий на основе древесины, а также других природных материалов
| Наименование материала | ρ кг/м³ |
λ₀ Вт/(м×℃) |
λА Вт/(м×℃) |
λБ Вт/(м×℃) |
|---|---|---|---|---|
| Хвойная древесина (сосна иди ель) поперек волокон | 500 | 0,09 | 0,14 | 0,18 |
| – они же — вдоль волокон | 500 | 0,18 | 0,29 | 0,35 |
| Древесина плотных лиственных пород (дуб, бук, ясень) поперек волокон | 700 | 0,1 | 0,18 | 0,23 |
| – они же — вдоль волокон | 700 | 0,23 | 0,35 | 0,41 |
| Клееная фанера | 600 | 0,12 | 0,15 | 0,18 |
| Облицовочный картон | 1000 | 0,18 | 0,21 | 0,23 |
| Картон строительный многослойный | 650 | 0,13 | 0,15 | 0,18 |
| Плиты древесно-волокнистые (ДВП), древесно-стружечные (ДСП), ориентированно-стружечные (ОСП) | 1000 | 0,15 | 0,23 | 0,29 |
| – то же, но для плотности | 800 | 0,13 | 0,19 | 0,23 |
| – то же, но для плотности | 600 | 0,11 | 0,13 | 0,16 |
| – то же, но для плотности | 400 | 0,08 | 0,11 | 0,13 |
| – то же, но для плотности | 200 | 0,06 | 0,07 | 0,08 |
| Плиты фибролитовые, арболит на основе портландцемента | 800 | 0,16 | 0,24 | 0,3 |
| – то же, но для плотности | 600 | 0,12 | 0,18 | 0,23 |
| – то же, но для плотности | 400 | 0,08 | 0,13 | 0,16 |
| – то же, но для плотности | 300 | 0,07 | 0,11 | 0,14 |
| Плиты камышитовые | 300 | 0,07 | 0,09 | 0,14 |
| – то же, но для плотности | 200 | 0,06 | 0,07 | 0,09 |
| Плиты торфяные термоизоляционные | 300 | 0,064 | 0,07 | 0,08 |
| – то же, но для плотности | 200 | 0,052 | 0,06 | 0,064 |
| Пакля строительная | 150 | 0,05 | 0,06 | 0,07 |
Таблица коэффициентов теплопроводности материалов, применяемых в термоизоляционных целях
| Наименование материала | ρ кг/м³ |
λ₀ Вт/(м×℃) |
λА Вт/(м×℃) |
λБ Вт/(м×℃) |
|---|---|---|---|---|
| Минеральная вата, стекловата | ||||
| Маты минеральной ваты прошивные или на синтетическом связующем | 125 | 0.056 | 0.064 | 0.07 |
| – то же, но для плотности | 75 | 0.052 | 0.06 | 0.064 |
| – то же, но для плотности | 50 | 0.048 | 0.052 | 0.06 |
| Плиты минеральной ваты на синтетическом и битумном связующих — мягкие, полужесткие и жесткие | 350 | 0.091 | 0.09 | 0.11 |
| – то же, но для плотности | 300 | 0.084 | 0.087 | 0.09 |
| – то же, но для плотности | 200 | 0.07 | 0.076 | 0.08 |
| – то же, но для плотности | 100 | 0.056 | 0.06 | 0.07 |
| – то же, но для плотности | 50 | 0.048 | 0.052 | 0.06 |
| Плиты минеральной ваты на органофосфатном связующем — повышенной жесткости | 200 | 0.064 | 0.07 | 0.076 |
| Плиты из стеклянного штапельного волокна на синтетическом связующем | 50 | 0.056 | 0.06 | 0.064 |
| Маты и полосы из стеклянного волокна прошивные | 150 | 0.061 | 0.064 | 0.07 |
| Синтетические утеплители | ||||
| Пенополистирол | 150 | 0.05 | 0.052 | 0.06 |
| – то же, но для плотности | 100 | 0.041 | 0.041 | 0.052 |
| – то же, но для плотности | 40 | 0.038 | 0.041 | 0.05 |
| Пенопласт ПХВ-1 и ПВ-1 | 125 | 0.052 | 0.06 | 0.064 |
| – то же, но для плотности | 100 и менее | 0.041 | 0.05 | 0.052 |
| Пенополиуретан плитный | 80 | 0.041 | 0.05 | 0.05 |
| – то же, но для плотности | 60 | 0.035 | 0.041 | 0.041 |
| – то же, но для плотности | 40 | 0.029 | 0.04 | 0.04 |
| Пенополиуретан напылением | 35 | 0.027 | 0.033 | 0.035 |
| Плиты из резольноформальдегидного пенопласта | 100 | 0.047 | 0.052 | 0.076 |
| – то же, но для плотности | 75 | 0.043 | 0.05 | 0.07 |
| – то же, но для плотности | 50 | 0.041 | 0.05 | 0.064 |
| – то же, но для плотности | 40 | 0.038 | 0.041 | 0.06 |
| Пенополиэтилен | 30 | 0.03 | 0.032 | 0.035 |
| Плиты из полиизоцианурата (PIR) | 35 | 0.024 | 0.028 | 0.031 |
| Перлитопласт-бетон | 200 | 0.041 | 0.052 | 0.06 |
| – то же, но для плотности | 100 | 0.035 | 0.041 | 0.05 |
| Перлитофосфогелевые изделия | 300 | 0.076 | 0.08 | 0.12 |
| – то же, но для плотности | 200 | 0.064 | 0.07 | 0.09 |
| Каучук вспененный | 85 | 0.035 | 0.04 | 0.045 |
| Утеплители на натуральной основе | ||||
| Эковата | 60 | 0.041 | 0.054 | 0.062 |
| – то же, но для плотности | 45 | 0.038 | 0.05 | 0.055 |
| – то же, но для плотности | 35 | 0.035 | 0.042 | 0.045 |
| Пробка техническая | 50 | 0.037 | 0.043 | 0.048 |
| Листы пробковые | 220 | 0.035 | 0.041 | 0.045 |
| Плиты льнокостричные термоизоляционные | 250 | 0.054 | 0.062 | 0.071 |
| Войлок строительный шерстяной | 300 | 0.057 | 0.065 | 0.072 |
| – то же, но для плотности | 150 | 0.045 | 0.051 | 0.059 |
| Древесные опилки | 400 | 0.092 | 1.05 | 1.12 |
| – то же, но для плотности | 200 | 0.071 | 0.078 | 0.085 |
| Засыпки минеральные | ||||
| Керамзит – гравий | 800 | 0.18 | 0.21 | 0.23 |
| – то же, но для плотности | 600 | 0.14 | 0.17 | 0.2 |
| – то же, но для плотности | 400 | 0.12 | 0.13 | 0.14 |
| – то же, но для плотности | 300 | 0.108 | 0.12 | 0.13 |
| – то же, но для плотности | 200 | 0.099 | 0.11 | 0.12 |
| Шунгизит – гравий | 800 | 0.16 | 0.2 | 0.23 |
| – то же, но для плотности | 600 | 0.13 | 0.16 | 0.2 |
| – то же, но для плотности | 400 | 0.11 | 0.13 | 0.14 |
| Щебень из доменного шлака, шлаковой пемзы и аглоперита | 800 | 0.18 | 0.21 | 0.26 |
| – то же, но для плотности | 600 | 0.15 | 0.18 | 0.21 |
| – то же, но для плотности | 400 | 1.122 | 0.14 | 0.16 |
| Щебень и песок из вспученного перлита | 600 | 0.11 | 0.111 | 0.12 |
| – то же, но для плотности | 400 | 0.076 | 0.087 | 0.09 |
| – то же, но для плотности | 200 | 0.064 | 0.076 | 0.08 |
| Вермикулит вспученный | 200 | 0.076 | 0.09 | 0.11 |
| – то же, но для плотности | 100 | 0.064 | 0.076 | 0.08 |
| Песок строительный сухой | 1600 | 0.35 | 0.47 | 0.58 |
| Пеностекло или газостекло | ||||
| Пеностекло или газо-стекло | 400 | 0.11 | 0.12 | 0.14 |
| – то же, но для плотности | 300 | 0.09 | 0.11 | 0.12 |
| – то же, но для плотности | 200 | 0.07 | 0.08 | 0.09 |
Таблица коэффициентов теплопроводности кровельных, гидроизоляционных, облицовочных, рулонных и наливных напольных покрытий
| Наименование материала | ρ кг/м³ |
λ₀ Вт/(м×℃) |
λА Вт/(м×℃) |
λБ Вт/(м×℃) |
|---|---|---|---|---|
| Асбестоцементные | ||||
| Листы асбестоцементные плоские («плоский шифер») | 1800 | 0.35 | 0.47 | 0.52 |
| – то же, но для плотности | 1600 | 0.23 | 0.35 | 0.41 |
| На битумной основе | ||||
| Битумы нефтяные строительные и кровельные | 1400 | 0.27 | 0.27 | 0.27 |
| – то же, но для плотности | 1200 | 0.22 | 0.22 | 0.22 |
| – то же, но для плотности | 1000 | 0.17 | 0.17 | 0.17 |
| Асфальтобетон | 2100 | 1.05 | 1.05 | 1.05 |
| Изделия из вспученного перлита на битумном связующем | 400 | 0.111 | 0.12 | 0.13 |
| – то же, но для плотности | 300 | 0.067 | 0.09 | 0.099 |
| Рубероид, пергамин, толь, гибкая черепица | 600 | 0.17 | 0.17 | 0.17 |
| Линолеумы и наливные полимерные полы | ||||
| Линолеум поливинилхлоридный многослойный | 1800 | 0.38 | 0.38 | 0.38 |
| – то же, но для плотности | 1600 | 0.33 | 0.33 | 0.33 |
| Линолеум поливинилхлоридный на тканевой подоснове | 1800 | 0.35 | 0.35 | 0.35 |
| – то же, но для плотности | 1600 | 0.29 | 0.29 | 0.29 |
| – то же, но для плотности | 1400 | 0.23 | 0.23 | 0.23 |
| Пол наливной полиуретановый | 1500 | 0.32 | 0.32 | 0.32 |
| Пол наливной эпоксидный | 1450 | 0.029 | 0.029 | 0.029 |
Таблица коэффициентов теплопроводности металлов и стекла
| Наименование материала | ρ кг/м³ |
λ₀ Вт/(м×℃) |
λА Вт/(м×℃) |
λБ Вт/(м×℃) |
|---|---|---|---|---|
| Сталь, в том числе – арматурная стержневая | 7850 | 58 | 58 | 58 |
| Чугун | 7200 | 50 | 50 | 50 |
| Алюминий | 2600 | 221 | 221 | 221 |
| Медь | 8500 | 407 | 407 | 407 |
| Бронза | 7500÷9300 | 25÷105 | 25÷105 | 25÷105 |
| Латунь | 8100÷8800 | 70÷120 | 70÷120 | 70÷120 |
| Стекло кварцевое оконное | 2500 | 0.76 | 0.76 | 0.76 |
Сейчас для утепления различных строений используются, преимущественно, синтетические материалы. Они имеют отличные характеристики, а также в большинстве своем очень удобны в монтаже.
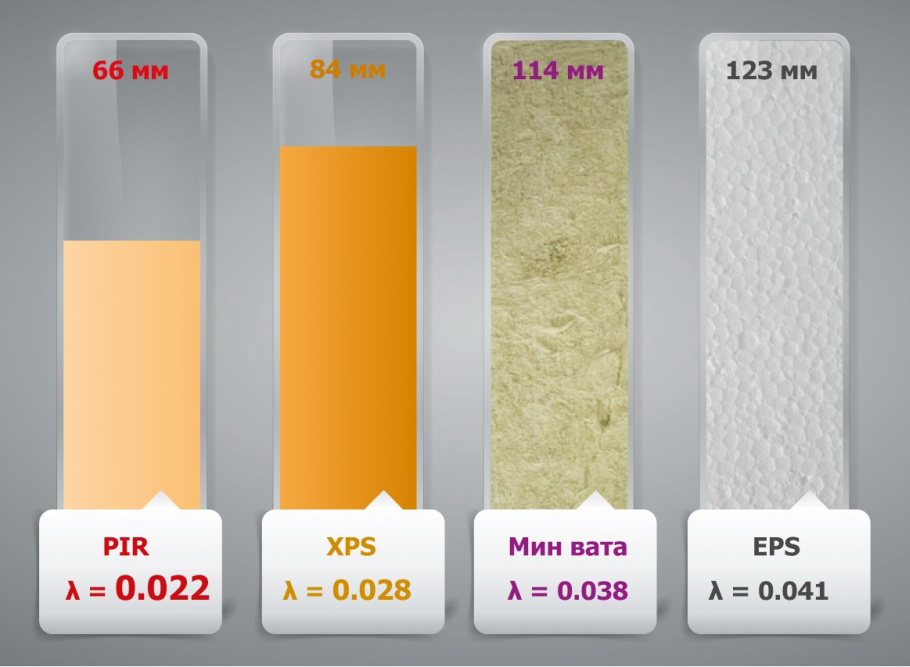
Исходя из значений в таблицах выше, из категории синтетических утеплителей одним из самых энергоэффективных является PIR-плита. При плотности всего 35 кг/м³ коэффициент теплопроводности у нее в среднем составляет 0,024 Вт/м*К. Но он может быть и меньше в зависимости от технологии производства PIR-плиты у того или иного производителя.
Так, например, PIR-плиты LOGICPIR от российского производителя ТЕХНОНИКОЛЬ имеют показатель теплопроводности всего 0,022 Вт/м*К. Почему значение так снижается? Дело в том, что этот вид утеплителя с обеих сторон имеет фольгированный слой. Фольга, как известно, сама по себе способна отлично отражать тепловую энергию в обратную сторону, то есть в помещение. Благодаря этому свойству энергоэффективность материала растет, а теплопотери в доме снижаются. Таким образом PIR-утеплитель, имеющий такой слой с одной и другой стороны, гораздо лучше выполняет свои функции, чем, например, PIR-материал с бумажным технологическим покрытием.
В целом же LOGICPIR — обычная PIR-плита, которая представляет собой пористый материал с множеством микроячеек, наполненных воздухом. Она очень тонкая (толщина варьируется в пределах 2-5 см), легкая, не нагружает строительные конструкции, но при этом прочная и достаточно плотная, чтобы выдерживать некоторые физические воздействия. Инертна к химическим воздействиям, биологически устойчива и, кроме того, не склонна к возгораниям.
Во время эксплуатации (а срок использования PIR-плит LOGICPIR составляет 50 лет) материал не теряет своих свойств. Его коэффициент теплопроводности не меняется даже при намокании: сам по себе утеплитель не впитывает воду. Дополнительную парозащиту обеспечивает и тот самый фольгированный слой — если при монтаже плит проклеить все стыки алюминиевым скотчем, то формируется непрерывный слой пароизоляции, не пропускающий влагу. Словом, это неплохой вариант синтетического утеплителя с одними из самых высоких характеристик.
Видео: Утепление каркасного дома PIR плитами
Для чего используются такие расчеты в практическом приложении?
Оценка эффективности имеющейся термоизоляции
А для чего бывает необходимо вычислять это сопротивление, какая от этого практическая польза?
Такими расчетами можно очень точно оценить степень термоизоляции своего жилья.
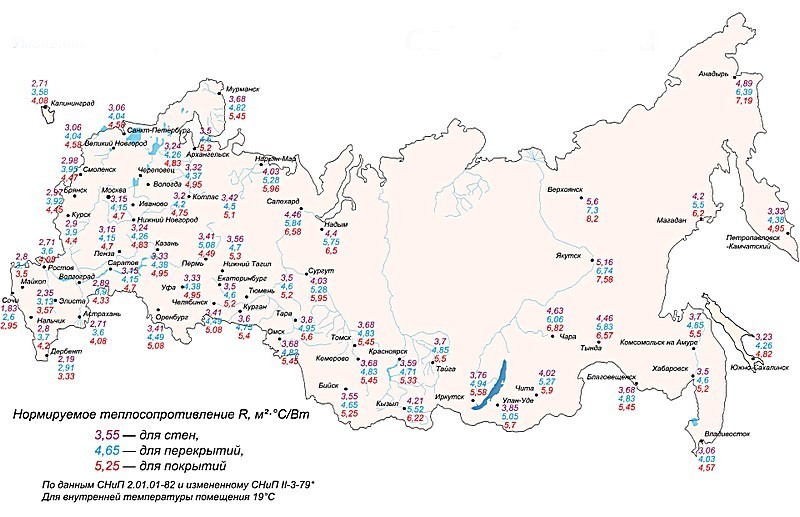
Дело в том, что для различных климатических регионов России специалистами рассчитаны так называемые нормативные показатели этого сопротивления теплопередаче, отдельно для стен, перекрытий и покрытий. То есть если сопротивление конструкции отвечает этой норме, то за утепление можно быть спокойным.
Значение этих нормированных сопротивлений для разных строительных конструкций можно найти, воспользовавшись предлагаемой картой схемой.
Если не дотягивает – надо принимать меры, усиливать термоизоляцию, чтобы минимизировать потери тепла. И, стало быть, решить обратную задачу. То есть с использованием той же формулы (сопротивление от коэффициента теплопроводности и толщины) найти ту толщину утепления, которая восполнит имеющийся «дефицит» до нормы.
Ну а если термоизоляции пока нет, то тут и вовсе все просто. Тогда потребуется определить, какой слой выбранного утеплительного материала обеспечит выход на нормированное значение сопротивления теплопередаче.
Определение уровня тепловых потерь
Еще одна важная задача – это определение величины тепловых потерь через ограждающую конструкцию. Такие вычисления бывают необходимы когда, например, определяется требуемая мощность системы отопления. Как по помещениям — для правильной расстановки обогревательных приборов (радиаторов), так и общая — для выбора оптимальной модели котла.
Дело в том, что это сопротивление описывается еще одной формулой, уже от разницы температур и количества тепла, уходящего через ограждающую конструкцию площадью один квадратный метр.
R = Δt / q
Δt — разница температур по обе стороны конструкции, ℃.
q — удельное количество теряемого тепла, Вт.
То есть если известна площадь ограждающей конструкции и ее термическое сопротивление (определенное, например, через толщину и коэффициент теплопроводности), если известно, для каких условий производится расчет (например, нормальная температура в помещении и самые сильные морозы, присущие данной местности), то можно спрогнозировать и тепловые потери через эту конструкцию.
Q = S × Δt/R
Q — теплопотери через ограждающую конструкцию, Вт.
S — площадь этой конструкции, м².
Такие расчеты в помещении проводятся для всех ограждающих конструкций, контактирующих с холодом, и затем определяется суммарные потери, которые должны компенсироваться системой отопления. Или, если эти потери получаются слишком большими – это становится побудительным мотивом к усовершенствованию системы термоизоляции – что-то с ней не так.
Еще одна ремарка. Это мы говорили о конструкциях, состоящих из нескольких слоев разных строительных и утеплительных материалов. А как быть с окнами? Как для них просчитывается сопротивление теплопередаче?
Методика здесь – несколько иная, и самостоятельно заниматься такими расчетами вряд ли имеет смысл. Можно воспользоваться таблицей, в которой уже имеются готовые значения сопротивления для различных типов конструкций окон.
Таблица приведенных значений сопротивления теплопередаче для окон, остекленных балконных дверей, световых проемов (фонарей)
| Материал и схема запонения проема | Приведенное термическое Ro, м ² × °С/Вт | |
|---|---|---|
| Д и ПВХ | А | |
| Двойное остекление в спаренных переплетах | 0.4 | – |
| Двойное остекление в раздельных переплетах | 0.44 | 0,34* |
| Тройное остекление в раздельно-спаренных переплетах | 0.55 | 0.46 |
| Однокамерный стеклопакет: | ||
| – из обычного стекла | 0.38 | 0.34 |
| – из стекла с твердым селективным покрытием | 0.51 | 0.43 |
| – из стекла с мягким селективным покрытием | 0.56 | 0.47 |
| Двухкамерный стеклопакет: | ||
| – из обычного стекла (с межстекольным расстоянием 6 мм) | 0.51 | 0.43 |
| – из обычного стекла (с межстекольным расстоянием 12 мм) | 0.54 | 0.45 |
| – из стекла с твердым селективным покрытием | 0.58 | 0.48 |
| – из стекла с мягким селективным покрытием | 0.68 | 0.52 |
| – из стекла с твердым селективным покрытием и заполнением аргоном | 0.65 | 0.53 |
| Обычное стекло и однокамерный стеклопакет в раздельных переплетах: | ||
| – из обычного стекла | 0.56 | – |
| – из стекла с твердым селективным покрытием | 0.65 | – |
| – из стекла с мягким селективным покрытием | 0.72 | – |
| – из стекла с твердым селективным покрытием и заполнением аргоном | 0.69 | – |
| Обычное стекло и двухкамерный стеклопакет в раздельных переплетах: | ||
| – из обычного стекла | 0.68 | – |
| – из стекла с твердым селективным покрытием | 0.74 | – |
| – из стекла с мягким селективным покрытием | 0.81 | – |
| – из стекла с твердым селективным покрытием и заполнением аргоном | 0.82 | – |
| Два однокамерных стеклопакета в спаренных переплетах | 0.7 | – |
| Два однокамерных стеклопакета в раздельных переплетах | 0.74 | – |
| Четырехслойное остекление в двух спаренных переплетах | 0.8 | – |
| Блоки стеклянные пустотные (с шириной кладочных швов 6 мм) размером: | ||
| -200×200 ×100 мм | 0,31 (без переплета) | |
| -250×250 ×100 мм | 0,33 (без переплета) | |
| Примечания: | ||
| Д и ПВХ – переплеты из дерева или пластика (поливинилхлорида) | ||
| А – переплеты из алюмииия | ||
| * – перепеты из стали | ||
| все указанные значения даны для площади остекления 75% от площади светового проема |
Понятно, что тепловые потери будут считаться, исходя из площади остекления и разницы температур.
Надо заметить, что профессиональные теплотехнические расчеты учитывают еще и множество различных поправочных коэффициентов, в том числе на инсоляцию (воздействие солнечных лучей), светопоглощающие и отражающие свойства поверхностей, неоднородность конструкций и другие. Но для самостоятельной первичной оценки достаточно и того алгоритма, что приведен выше.
Для любителей же более обстоятельного подхода можно порекомендовать следующий видеосюжет:
Видео: Алгоритмы профессионального расчета сопротивления теплопередаче стен
Мы же завершим публикацию онлайн-калькулятором, который вполне позволяет на бытовом уровне решить ряд задач, о которых шла речь выше.
Калькулятор расчета термического сопротивления ограждающей конструкции
Перейти к расчётам
Пояснения по работе с калькулятором
Программа несложна, но все же требует некоторых пояснений.
Предлагаемый алгоритм расчета позволяет провести вычисления сопротивления теплопередаче для любой ограждающей конструкции, включающей от одного до пяти различных слоев.
- Первый слой пусть будет считаться по умолчанию основным. Для него указывается:
— его толщина в миллиметрах (так сделано для удобства, а перевод в метры программа выполнит самостоятельно).
— коэффициент теплопроводности материала, из которого создан этот слой. Значение берется из таблиц, с учетом режима эксплуатации А или Б. При вводе значения в калькулятор вместо запятой в качестве десятичного разделителя используется точка.
- Вторым слоем предлагается указать имеющуюся (если есть) или планируемую термоизоляцию. Здесь уже на выбор – если оставить по умолчанию «нет», то программа проигнорирует этот слой. Если согласиться – появятся поля ввода данных, те же толщина и коэффициент теплопроводности.
- Аналогично по выбору пользователя вводятся или игнорируются еще три произвольных слоя. Это, кстати, могут быть внешняя и внутренняя отделка, если она выполнена из значимых для теплопроводности материалов, многослойная кладка стены и т.п.
- Если задача стоит только в определении сопротивления теплопередаче, то можно сразу переходить к клавише «РАССЧИТАТЬ…».
- Ну а если есть желание еще и найти величину тепловых потерь через рассчитываемую ограждающую конструкцию, то ставится отметка «да, включить дополнительный расчёт». В этом случае появятся еще три поля ввода данных – площадь ограждающей конструкции, температура в помещении и температура на улице.
Уличную температуру для расчетов, как правило, берут минимальную, свойственную самой холодной декаде зимы в регионе проживания. Так задается необходимый запас мощности отопительного оборудования и эффективности системы утепления. Домашнюю температуру обычно считают в пределах 20÷24 ℃ для жилых помещений. Для нежилых (подъезды, коридоры, кладовые и т.п.) можно ограничиться +15 ℃. Для ванных, душевых, бань – порядка 35 ℃.
Рассчитанное термическое сопротивление показывается первой строкой появляющегося результата. Если был выбран вариант с вычислением тепловых потерь, то их значение (в ваттах) будет указано во второй строке.
In thermodynamics, the heat transfer coefficient or film coefficient, or film effectiveness, is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat (i.e., the temperature difference, ΔT ). It is used in calculating the heat transfer, typically by convection or phase transition between a fluid and a solid. The heat transfer coefficient has SI units in watts per square meter per kelvin (W/m2/K).
The overall heat transfer rate for combined modes is usually expressed in terms of an overall conductance or heat transfer coefficient, U. In that case, the heat transfer rate is:
where (in SI units):
- A: surface area where the heat transfer takes place (m2)
- T2: temperature of the surrounding fluid (K)
- T1: temperature of the solid surface (K)
The general definition of the heat transfer coefficient is:
where:
- q: heat flux (W/m2); i.e., thermal power per unit area,
- ΔT: difference in temperature between the solid surface and surrounding fluid area (K)
The heat transfer coefficient is the reciprocal of thermal insulance. This is used for building materials (R-value) and for clothing insulation.
There are numerous methods for calculating the heat transfer coefficient in different heat transfer modes, different fluids, flow regimes, and under different thermohydraulic conditions. Often it can be estimated by dividing the thermal conductivity of the convection fluid by a length scale. The heat transfer coefficient is often calculated from the Nusselt number (a dimensionless number). There are also online calculators available specifically for Heat-transfer fluid applications. Experimental assessment of the heat transfer coefficient poses some challenges especially when small fluxes are to be measured (e.g. < 0.2 W/cm2).[1][2]
Composition[edit]
A simple method for determining an overall heat transfer coefficient that is useful to find the heat transfer between simple elements such as walls in buildings or across heat exchangers is shown below. Note that this method only accounts for conduction within materials, it does not take into account heat transfer through methods such as radiation. The method is as follows:
Where:
As the areas for each surface approach being equal the equation can be written as the transfer coefficient per unit area as shown below:
or
Often the value for 
In the walls of buildings the above formula can be used to derive the formula commonly used to calculate the heat through building components. Architects and engineers call the resulting values either the U-Value or the R-Value of a construction assembly like a wall. Each type of value (R or U) are related as the inverse of each other such that R-Value = 1/U-Value and both are more fully understood through the concept of an overall heat transfer coefficient described in lower section of this document.
Convective heat transfer correlations[edit]
Although convective heat transfer can be derived analytically through dimensional analysis, exact analysis of the boundary layer, approximate integral analysis of the boundary layer and analogies between energy and momentum transfer, these analytic approaches may not offer practical solutions to all problems when there are no mathematical models applicable. Therefore, many correlations were developed by various authors to estimate the convective heat transfer coefficient in various cases including natural convection, forced convection for internal flow and forced convection for external flow. These empirical correlations are presented for their particular geometry and flow conditions. As the fluid properties are temperature dependent, they are evaluated at the film temperature 


External flow, vertical plane[edit]
Recommendations by Churchill and Chu provide the following correlation for natural convection adjacent to a vertical plane, both for laminar and turbulent flow.[3][4] k is the thermal conductivity of the fluid, L is the characteristic length with respect to the direction of gravity, RaL is the Rayleigh number with respect to this length and Pr is the Prandtl number.
(Note: The Rayleigh number can be written as the product of the Grashof number and the Prandtl number)
For laminar flows, the following correlation is slightly more accurate. It is observed that a transition from a laminar to a turbulent boundary occurs when RaL exceeds around 109.
External flow, vertical cylinders[edit]
For cylinders with their axes vertical, the expressions for plane surfaces can be used provided the curvature effect is not too significant. This represents the limit where boundary layer thickness is small relative to cylinder diameter 
where 
External flow, horizontal plates[edit]
W. H. McAdams suggested the following correlations for horizontal plates.[5] The induced buoyancy will be different depending upon whether the hot surface is facing up or down.
For a hot surface facing up, or a cold surface facing down, for laminar flow:
and for turbulent flow:
For a hot surface facing down, or a cold surface facing up, for laminar flow:
The characteristic length is the ratio of the plate surface area to perimeter. If the surface is inclined at an angle θ with the vertical then the equations for a vertical plate by Churchill and Chu may be used for θ up to 60°; if the boundary layer flow is laminar, the gravitational constant g is replaced with g cos θ when calculating the Ra term.
External flow, horizontal cylinder[edit]
For cylinders of sufficient length and negligible end effects, Churchill and Chu has the following correlation for 
External flow, spheres[edit]
For spheres, T. Yuge has the following correlation for Pr≃1 and 
Vertical rectangular enclosure[edit]
For heat flow between two opposing vertical plates of rectangular enclosures, Catton recommends the following two correlations for smaller aspect ratios.[7] The correlations are valid for any value of Prandtl number.
For 
where H is the internal height of the enclosure and L is the horizontal distance between the two sides of different temperatures.
For 
For vertical enclosures with larger aspect ratios, the following two correlations can be used.[7] For 10 < H/L < 40:
For 
For all four correlations, fluid properties are evaluated at the average temperature—as opposed to film temperature—



Forced convection[edit]
Internal flow, laminar flow[edit]
Sieder and Tate give the following correlation to account for entrance effects in laminar flow in tubes where 


For fully developed laminar flow, the Nusselt number is constant and equal to 3.66. Mills combines the entrance effects and fully developed flow into one equation
[8]
Internal flow, turbulent flow[edit]
The Dittus-Bölter correlation (1930) is a common and particularly simple correlation useful for many applications. This correlation is applicable when forced convection is the only mode of heat transfer; i.e., there is no boiling, condensation, significant radiation, etc. The accuracy of this correlation is anticipated to be ±15%.
For a fluid flowing in a straight circular pipe with a Reynolds number between 10,000 and 120,000 (in the turbulent pipe flow range), when the fluid’s Prandtl number is between 0.7 and 120, for a location far from the pipe entrance (more than 10 pipe diameters; more than 50 diameters according to many authors[9]) or other flow disturbances, and when the pipe surface is hydraulically smooth, the heat transfer coefficient between the bulk of the fluid and the pipe surface can be expressed explicitly as:
where:
is the hydraulic diameter
is the thermal conductivity of the bulk fluid
is the fluid viscosity
mass flux
isobaric heat capacity of the fluid
is 0.4 for heating (wall hotter than the bulk fluid) and 0.33 for cooling (wall cooler than the bulk fluid).[10]
The fluid properties necessary for the application of this equation are evaluated at the bulk temperature thus avoiding iteration.
Forced convection, external flow[edit]
In analyzing the heat transfer associated with the flow past the exterior surface of a solid, the situation is complicated by phenomena such as boundary layer separation. Various authors have correlated charts and graphs for different geometries and flow conditions.
For flow parallel to a plane surface, where 

Thom correlation[edit]
There exist simple fluid-specific correlations for heat transfer coefficient in boiling. The Thom correlation is for the flow of boiling water (subcooled or saturated at pressures up to about 20 MPa) under conditions where the nucleate boiling contribution predominates over forced convection. This correlation is useful for rough estimation of expected temperature difference given the heat flux:[11]

where:
is the wall temperature elevation above the saturation temperature, K
- q is the heat flux, MW/m2
- P is the pressure of water, MPa
Note that this empirical correlation is specific to the units given.
Heat transfer coefficient of pipe wall[edit]
The resistance to the flow of heat by the material of pipe wall can be expressed as a “heat transfer coefficient of the pipe wall”. However, one needs to select if the heat flux is based on the pipe inner or the outer diameter.
Selecting to base the heat flux on the pipe inner diameter, and assuming that the pipe wall thickness is small in comparison with the pipe inner diameter, then the heat transfer coefficient for the pipe wall can be calculated as if the wall were not curved[citation needed]:
where k is the effective thermal conductivity of the wall material and x is the wall thickness.
If the above assumption does not hold, then the wall heat transfer coefficient can be calculated using the following expression:
where di and do are the inner and outer diameters of the pipe, respectively.
The thermal conductivity of the tube material usually depends on temperature; the mean thermal conductivity is often used.
Combining convective heat transfer coefficients[edit]
For two or more heat transfer processes acting in parallel, convective heat transfer coefficients simply add:
For two or more heat transfer processes connected in series, convective heat transfer coefficients add inversely:[12]
For example, consider a pipe with a fluid flowing inside. The approximate rate of heat transfer between the bulk of the fluid inside the pipe and the pipe external surface is:[13]
where
- q = heat transfer rate (W)
- h = convective heat transfer coefficient (W/(m2·K))
- t = wall thickness (m)
- k = wall thermal conductivity (W/m·K)
- A = area (m2)
= difference in temperature.
Overall heat transfer coefficient[edit]
The overall heat transfer coefficient 
For the case of a heat exchanger, 
where:
= heat transfer rate (W)
= overall heat transfer coefficient (W/(m2·K))
= heat transfer surface area (m2)
= logarithmic mean temperature difference (K).
The overall heat transfer coefficient takes into account the individual heat transfer coefficients of each stream and the resistance of the pipe material. It can be calculated as the reciprocal of the sum of a series of thermal resistances (but more complex relationships exist, for example when heat transfer takes place by different routes in parallel):
where:
- R = Resistance(s) to heat flow in pipe wall (K/W)
- Other parameters are as above.[14]
The heat transfer coefficient is the heat transferred per unit area per kelvin. Thus area is included in the equation as it represents the area over which the transfer of heat takes place. The areas for each flow will be different as they represent the contact area for each fluid side.
The thermal resistance due to the pipe wall (for thin walls) is calculated by the following relationship:
where
- x = the wall thickness (m)
- k = the thermal conductivity of the material (W/(m·K))
This represents the heat transfer by conduction in the pipe.
The thermal conductivity is a characteristic of the particular material. Values of thermal conductivities for various materials are listed in the list of thermal conductivities.
As mentioned earlier in the article the convection heat transfer coefficient for each stream depends on the type of fluid, flow properties and temperature properties.
Some typical heat transfer coefficients include:
- Air – h = 10 to 100 W/(m2K)
- Water – h = 500 to 10,000 W/(m2K).
Thermal resistance due to fouling deposits[edit]
Often during their use, heat exchangers collect a layer of fouling on the surface which, in addition to potentially contaminating a stream, reduces the effectiveness of heat exchangers. In a fouled heat exchanger the buildup on the walls creates an additional layer of materials that heat must flow through. Due to this new layer, there is additional resistance within the heat exchanger and thus the overall heat transfer coefficient of the exchanger is reduced. The following relationship is used to solve for the heat transfer resistance with the additional fouling resistance:[15]
=
where
= overall heat transfer coefficient for a fouled heat exchanger,
= perimeter of the heat exchanger, may be either the hot or cold side perimeter however, it must be the same perimeter on both sides of the equation,
= overall heat transfer coefficient for an unfouled heat exchanger,
= fouling resistance on the cold side of the heat exchanger,
= fouling resistance on the hot side of the heat exchanger,
= perimeter of the cold side of the heat exchanger,
= perimeter of the hot side of the heat exchanger,
This equation uses the overall heat transfer coefficient of an unfouled heat exchanger and the fouling resistance to calculate the overall heat transfer coefficient of a fouled heat exchanger. The equation takes into account that the perimeter of the heat exchanger is different on the hot and cold sides. The perimeter used for the 

The fouling resistances can be calculated for a specific heat exchanger if the average thickness and thermal conductivity of the fouling are known. The product of the average thickness and thermal conductivity will result in the fouling resistance on a specific side of the heat exchanger.[15]
=
where:
= average thickness of the fouling in a heat exchanger,
= thermal conductivity of the fouling,
.
See also[edit]
- Convective heat transfer
- Heat sink
- Convection
- Churchill–Bernstein equation
- Heat
- Heat pump
- Heisler Chart
- Thermal conductivity
- Thermal-hydraulics
- Biot number
- Fourier number
- Nusselt number
References[edit]
- ^ Chiavazzo, Eliodoro; Ventola, Luigi; Calignano, Flaviana; Manfredi, Diego; Asinari, Pietro (2014). “A sensor for direct measurement of small convective heat fluxes: Validation and application to micro-structured surfaces” (PDF). Experimental Thermal and Fluid Science. 55: 42–53. doi:10.1016/j.expthermflusci.2014.02.010.
- ^ Maddox, D.E.; Mudawar, I. (1989). “Single- and Two-Phase Convective Heat Transfer From Smooth and Enhanced Microelectronic Heat Sources in a Rectangular Channel”. Journal of Heat Transfer. 111 (4): 1045–1052. doi:10.1115/1.3250766.
- ^ Churchill, Stuart W.; Chu, Humbert H.S. (November 1975). “Correlating equations for laminar and turbulent free convection from a vertical plate”. International Journal of Heat and Mass Transfer. 18 (11): 1323–1329. doi:10.1016/0017-9310(75)90243-4.
- ^ Sukhatme, S. P. (2005). A Textbook on Heat Transfer (Fourth ed.). Universities Press. pp. 257–258. ISBN 978-8173715440.
- ^ McAdams, William H. (1954). Heat Transmission (Third ed.). New York: McGraw-Hill. p. 180.
- ^ a b c James R. Welty; Charles E. Wicks; Robert E. Wilson; Gregory L. Rorrer (2007). Fundamentals of Momentum, Heat and Mass transfer (5th ed.). John Wiley and Sons. ISBN 978-0470128688.
- ^ a b Çengel, Yunus. Heat and Mass Transfer (Second ed.). McGraw-Hill. p. 480.
- ^ Subramanian, R. Shankar. “Heat Transfer in Flow Through Conduits” (PDF). clarkson.edu.
- ^ S. S. Kutateladze; V. M. Borishanskii (1966). A Concise Encyclopedia of Heat Transfer. Pergamon Press.
- ^ F. Kreith, ed. (2000). The CRC Handbook of Thermal Engineering. CRC Press.
- ^ W. Rohsenow; J. Hartnet; Y. Cho (1998). Handbook of Heat Transfer (3rd ed.). McGraw-Hill.
- ^ This relationship is similar to the harmonic mean; however, note that it is not multiplied with the number n of terms.
- ^ “Heat transfer between the bulk of the fluid inside the pipe and the pipe external surface”. physics.stackexchange.com. Retrieved 15 December 2014.
- ^ Coulson and Richardson, “Chemical Engineering”, Volume 1, Elsevier, 2000
- ^ a b A.F. Mills (1999). Heat Transfer (second ed.). Prentice Hall, Inc.
External links[edit]
- Overall Heat Transfer Coefficients
- Overall Heat Transfer Coefficients Table and Equation
- Correlations for Convective Heat Transfer
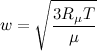











 Кстати, о влажности!..
Кстати, о влажности!..